О некоторых работах братьев Я. и И. Бернулли

Весь XVII век богат именами ученых, заложивших основы современных физикоматематических наук. В первой половине века это были С. Стевин, Г. Галилей, И. Кеплер, Р. Декарт, П. Ферма, Ж. Роберваль. От них эстафету приняли Дж. Уоллес, Э. Мариотт, Б. Паскаль, Р. Бойль, Х. Гюйгенс, Р. Гук, И. Ньютон, Г.В. Лейбниц, П. Вари-ньон. В конце XVII в. значительный вклад в постановку новых и модернизацию уже известных задач механики, в адаптацию к ним дифференциального и интегрального исчисления внесли известные швейцарские математики и механики братья Якоб и Иоганн Бернулли.

Якоб Бернулли (Jakob Bernoulli, 06.01.1655–27.08.1705) был профессором математики и физики Базельского университета (с 1687 г.), членом Парижской (с 1699 г.) и Берлинской (с 1701 г.) академий наук, одним из основателей математического анализа, вариационного исчисления, аналитической геометрии, комбинаторики, теории вероятности и теории чисел.

Будучи студентом Базельского университета, Якоб изучал богословие, французский, итальянский, английский, латинский, греческий языки, в 1671 г. получил ученую степень магистра философии. В студенческие годы начал самостоятельное изучение математики. После университета он путешествовал по Франции, Италии, Нидерландам, Англии, где познакомился со многими учеными, в частности, с Гюйгенсом, Бойлем, Гуком. Вернувшись в Базель, начал читать в университете лекции по физике и математике.

Познакомившись с первой публикацией Лейбница по анализу (1684), начал самостоятельное освоение нового исчисления и приобщил к этому младшего брата Иоганна. Позднее между Лейбницем и братьями завязалась многолетняя и очень плодотворная переписка. В 1690 г. Якоб решил задачу Лейбница о форме кривой, по которой тяжелая точка опускается за равные промежутки времени на равные вертикальные отрезки. Лейбниц, исходя из своего принципа сохранения

живых сил v² –v 0 ² = 2g(y – y 0 ), и Гюйгенс, используя геометрическое решение, установили, что это полукубическая парабола. Однако Якоб получил этот результат средствами нового анализа, выведя и проинтегрировав дифференциальное уравнение. Так впервые появился термин "интеграл".

Принцип, заложенный Гюйгенсом в решение задачи о центре колебаний, некоторым ученым казался сомнительным и поэтому Я. Бернулли предложил свое решение, основанное на идее компенсации движущих сил силами инерции, получившей дальнейшее развитие у Германна, Эйлера, Даламбера и, благодаря Лагранжу, вошедшей в теоретическую механику под названием "принцип Даламбера". Современный вид принцип Даламбера принял после выхода в 1856 г. "Трактата рациональной механики" Ш. Делоне (1816– 1872).

Решение Якобом Бернулли задачи о центре качаний (колебаний), опубликованное в "Acta eruditorum" (1691) и "Мемуарах" Парижской академии наук (1703), сводится к следующему.

Пусть в точках a и a (рис. 1) жесткого невесомого стержня Aa , совершающего колебания около неподвижной точки A, укреплены две точечные массы m и m . Необходимо найти длину изохронного математического маятника или расстояние l₀ = Aa₀ до точки a ₀, в которой сосредоточена масса m ₀ = m_x + m ₂, если Aa_x = l j, Aa₂ = l₂ .

пройдет путь ab > aO, точка a0 - путь ab « a0N, точка a2 - путь a2b2 < a2Q Пока точка a не достигла положения c , все точки "падали" свободно. Но в положении c , как говорит Я. Бернулли, "действие веса точки a истощилось" [1, c.150] и она продолжает свое движение к точке b за счет веса точки a .

За время прохождения точкой a дуги c b точка a пройдет меньшую дугу c b , то есть точка a действует на a замедляющим образом. Таким образом, точка a своей инерцией (силой инерции) замедляет вращение стержня, а точка a – его ускоряет, точка a не вносит никакого вклада, оставаясь в данный момент как бы неподвижной. В таком случае стержень Aa можно отождествлять с рычагом второго рода с точкой опоры в А, находящимся в равновесии под действием сил инерции m c b и m c b грузов m и m , направленных в противоположные стороны. Уравнение равновесия рычага mj^ ■ cb = m2l2 ■ c2b2, из-за малости дуг cb = li (a — a ),

Oa cb = l2 (a2—a0) и углов a ~ tga = —1;

l 1

Qa      Na a2 =---— ; a0 =---0, после преобразований

2       _{l 2}        0       _{l 0}

приводит к искомому выражению:

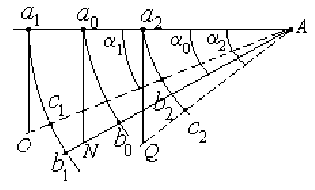
Рис. 1

Если бы стержень свободно падал под действием тяжести грузов m, и m ₂, то за Д t точки a , a , a переместились бы в положения O , N , Q , причем Oa = Na₀ = Qa₂ . Но стержень поворачивается вокруг точки А и через Д t займет положение AN , точка a

_ mJ— + m2lf ml + m2l2

.

Для случая нескольких масс решение будет аналогичным. Кроме идеи сведения изучения движения тела к изучению его равновесия с учетом сил инерции, Я. Бернулли высказал мысль о возможном определении реакции связи. Истинное движение ac ( a₂b₂ ) он разложил на свободное aO ( a₂Q ) и движение Oc ( Qb — ) вдоль стержня. Каждому движению он ставит в соответствие силу. Вертикальному движению aO ( a₂Q ) , естественно, соответствует сила тяжести, а сила, соответствующая движению вдоль стержня,

уравновешивается опорой А . По современным

представлениям – реакцией связи.

Ученик Я. Бернулли – первый академик Петербургской академии наук Якоб Герман (Jakob Hermann, 1678–1733), дал иную интерпретацию идеи использования сил инерции. В наиболее из- вестном сочинении "Форономия или две кни- ги о силах и движениях твердых и жидких тел", решая задачу о нахождении центра колебаний физического маятника, он разлагает силу тяжести каждой материальной точки на две составляющие: одна направлена по линии подвеса, другая – перпендикулярно первой. Первая из сил уравновешивается реакцией связи (опора А), вторая – силой инерции, равной массе точки, умноженной на касательное ускорение (по закону ускоряющих сил Ньютона). Это рассуждение относится к каждой точке маятника, то есть к маятнику в целом и, в современной трактовке, приводит к следующему принципу: в каждый момент времени движущие силы (вес), реакции связи и силы инерции уравновешиваются.

Воспользовавшись этим принципом для решения своей задачи, Герман не придал ему всеобщего статуса. Это сделал позднее другой академик Петербургской академии наук, ученик И. Бернулли – Леонард Эйлер, использовавший сформулированный принцип (в своей интерпретации) для решения многих задач, в том числе и не связанных с колебаниями тел. Интерпретация Эйлера была такова. Пусть тело движется по плоскости под действием силы F , приложенной к центру масс тела. Разложим F на касательную F τ и нормальную F n составляющие. Сила F n уравновесится реакцией плоскости, сила F τ вызовет ускоренное движение или силу инерции m a . Если силу инерции направить противоположно ускорению a , то можно считать, что она "уравновешивает" F τ . Иначе говоря, в каждый момент времени F , m a и реакции поверхности уравновешиваются.

Исключительно важен вклад Я. Бернулли в основы механики сплошных сред. Им сформулирована так называемая гипотеза плоских сечений, используемая в теории балок. Эта гипотеза утверждает, что поперечные сечения балки, которые до деформации были ортогональны упругой линии, после дефор- мации остаются ортогональными деформированной упругой линии. Во второй половине XX в. было теоретически доказано, что для тонких стержней эта гипотеза выполняется с очень высокой степенью точности.

В 1673 г. французский математик и механик, последователь Декарта и критик ньютоновской теории света Гастон Парди (Gaston-Ignace Pardis, 1636–1673) сформулировал принцип затвердевания применительно к гибким нитям (подвесным мостам, цепным линиям и т.д.): форма любой выделенной части нити не изменится, если отброшенную часть нити заменить подходящими силами, приложенными к концам выделенной части нити и направленными вдоль касательных к нити в концевых точках. Именно в такой форме принцип был использован Якобом Бернулли в его исследованиях по гибким балкам и нитям. В 1691 г. Я. Бернулли вывел дифференциальные уравнения равновесия гибких нитей при действии произвольной распределенной нагрузки, уравнения изгиба балки (консольной, закрепленной по концам).

Как математик Якоб Бернулли внес существенный вклад в разработку основ дифференциального и интегрального исчислений, аналитической геометрии, теории вероятности и вариационного исчисления. Он решил проблему Лейбница об изохронной кривой, исследовал логарифмическую спираль, ввел полярные координаты. В 1685 г. сформулировал, а в 1687–1689 доказал закон больших чисел (названный так позднее Пуассоном). Его главный труд "Искусство предположений", посвященный теории вероятностей, был опубликован лишь в 1713. Умер Якоб Бернулли в Базеле 16 августа 1705 г.

Своим интересом к математическим проблемам Якоб увлек и своего младшего брата Иоганна Бернулли (Johann Bernoulli, 27.07.1667– 01.01.1748). В 1683 г. Иоганн, как ранее и его старший брат, по-

ступил в Базельский университете, где, после завершения учебы, последовательно защитил бакалаврскую и магистерскую диссертации.

С 1685 г. он, по совету брата, начал са- мостоятельно изучать математику, механику (труды древнегреческих ученых, "Геометрию"

Декарта, публикации Лейбница) и медицину. В 1690 г. он защитил диссертацию на степень лиценциата медицины и, по семейной традиции, отправился в путешествие по Европе. В Париже Иоганн познакомился с известными учеными, в частности, с маркизом де Лапита-лем. По просьбе нового друга, Бернулли рассказал ему о первых работах по дифференциальному и интегральному исчислению.

В 1692 г. Иоганн вернулся в Базель, где продолжил занятия математикой и медициной. В 1694 г. он защитил диссертацию на степень доктора медицины, женился и вскоре переехал в г. Гронинген (Нидерланды), где следующие 10 лет работал профессором математики и экспериментальной физики Гронингенского университета. За годы работы в Гронингене И. Бернулли создал этому университету славу одного из главных математических центров Европы. А после смерти старшего брата Якоба, в 1705 г. Иоганн вернулся в Базель и следующие 43 года был профессором математики (8 раз избирался деканом и дважды ректором) Базельского университета.

У Иоганна было четыре дочери и пять сыновей, трое из которых (Николай, Даниил, Иоганн) стали известными математиками и механиками. Николай и Даниил были в числе первых академиков Петербургской академии наук. Любовь к математическим наукам Иоганн Бернулли привил не только сыновьям, но и своему знаменитому ученику Леонарду Эйлеру.

Лейбниц и братья Бернулли были инициаторами решения нескольких задач (о цепной линии, о брахистрохроне, о геодезической, …), привлекших внимание многих европейских ученых (Гюйгенса, Ньютона, Ла-питаля, …), ставших своеобразным полигоном для использования нового математического анализа и создания новых разделов математики (дифференциальные уравнения, вариационное исчисление, аналитическая и дифференциальная геометрия,…).

Одной из самых известных задач, сформулированных и решенных И. Бернулли, была задача о брахистохроне (1696), то есть о линии, по которой тело проходит от одной точки до другой за кратчайшее время. В своем решении Бернулли исходил из принципа Ферма: "...луч света, проходящий из более редкой cреды в более плотную, отклоняется к перпендикуляру таким образом, что за данный промежуток времени луч (который по предположению проходит последовательно от точки, испускающей свет, до освещае- мой точки) совершает кратчайший путь" [1, c. 169].

До Эйлера под синусом угла понималась длина перпендикуляра, опущенного в единичном круге из конца подвижного радиуса на неподвижный. Ферма показал, что синус угла падения относится к синусу угла преломления как разреженности сред, или в обратном отношении их плотностей, или в отношении скоростей луча (точки) в средах. Этот результат был подтвержден Лейбницем (Acta eruditorum, 1682) и Гюйгенсом ("Трактат о свете"). Считая, что среда имеет переменную плотность, Бернулли разбивает ее на бесконечно большое количество горизонтальных слоев с постоянной плотностью. При этом луч (шарик), перемещаясь от слоя к слою, будет описывать некоторую ломаную, каждое звено которой является траекторией быстрейшего перемещения точки внутри отдельного слоя (от точки к точке). Эта линия будет траекторией точки, проходящей через среду, с разреженностью пропорциональной скорости вертикального падения точки (с соответствующим ускорением).

Пусть точка движется из положения А (рис. 2) по искомой кривой АМ , со скоростями, задаваемыми кривой AH, AC = x , CM = y , Cc = dx , mn = dy , Mm = dz , CH = t (скорость (пропорциональная времени) в положении M ), a = const (скорость за время перехода из M в m, т.е. по dz, считается постоянной, равной a), sin а ~ dy , sin а ~ dz .

На основании принципа Ферма dy dz ta

Но dz = ^ (dx)2 + (dy)2 , поэтому полу- ченное равенство приводит к уравнению a2 (dy )2 = t2 (dx )2 +12 (dy )2, из которого следует дифференциальное уравнение для траектории АМ dy =

tdx

22 v a — t

По закону Галилея, кривая AH является параболой t ² = ax .

В таком случае полученное дифференци- альное уравнение принимает вид dy = J x dx.

\ a — x

Решение этого уравнения и является искомой кривой АМ – брахистохроной.

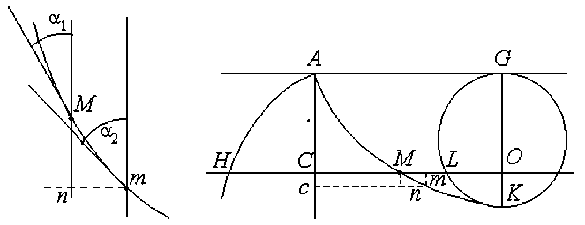
Рис. 2

В таком случае полученное дифференци-

альное уравнение принимает вид

dy =

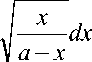
Решение этого интеграла и является искомой кривой АМ – брахистохроной.

Но Бернулли обращает внимание и на то, что брахистохрона является той же самой кривой, которая была получена Гюйгенсом при исследовании колебаний маятника. Это циклоида. Действительно, если считать, что круг GLK диаметром a катится без проскальзывания по линии AG , то можно показать, что

точка K его окружности будет описывать кри-

вую (циклоиду)

y = \

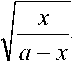
dx + C ,

где

x = AC , y = CM . Это совпадение, отмечает автор, "вытекает только из основного положения Галилея; уже из этого можно было бы заключить, что это положение находится в согласии с природой. Природа всегда действует простейшим образом, – так и в данном случае она с помощью одной и той же линии оказывает две различных услуги" [1, c. 171].

Отметим, что решение задачи о брахистохроне было чисто кинематическим, основанным на законах Ферма и Галилея, и использовало идеи нового математического анализа. Оно было традиционным, но сама постановка задачи – определение движения, отвечающего некоторому экстремальному критерию, – оказалась чрезвычайно перспективной. Перспективной и с точки зрения формирования нового раздела математики – вариационного исчисления, как метода постановки и решения экстремальных задач, так и с точки зрения перспективы открытия новых принципов движения тел природы. Мысль о том, что "...природа всегда действует простейшим образом" , стала отправной в по-

исках критериев движения и равновесия тел (минимум времени, пути, действия, высоты центра тяжести, потенциальной энергии,...), играющих роль законов природы. И аппарат вариационного исчисления, а позднее и теории оптимального управления, стал одним из основных методов аналитической механики.

Важнейшую роль в формировании идеологии и методологии механики сыграли многочисленные работы Иоганна Бернулли, принесшие ему мировую известность. Эти работы начинались как развитие идей математического анализа и динамики Лейбница и вылились в обширный цикл задач, сформулированных Галилеем, Гюйгенсом, Лейбницем, Ньютоном, им самим, как правило, решаемых методами дифференциального и интегрального исчисления (термин И. Бернулли) на основе принципов и законов механики XVII в.

Для истории теоретической механики наибольший интерес представляет сочинение "Рассуждение о законах передачи движения", представленное в 1724 г. на конкурс Парижской академии наук. Знакомство с содержанием этой работы позволит получить представление о состоянии механики в первой трети XVIII в. Вопрос, предложенный для конкурсного решения, состоял в следующем: "Каковы те законы, согласно которым совершенно твердое движущееся тело приводит в движение другое такое же, находящееся в покое или в движении, тело, которое оно встречает в пустоте или же в среде?" [1, c. 156]. По-видимому, подобная постановка проблемы свидетельствовала о некотором недоверии принципам механики Декарта, Ньютона, Гюйгенса, Лейбница и должна была стать стимулом для поиска новых принципов и более убедительных доказательств.

Разъяснение своей позиции ("Философ и геометр, обязанные соблюдать в своих доказательствах ясность и очевидность, должны за-

ботливо избегать какой бы то ни было двусмысленности в выражениях" [1, c. 156–157]) автор начинает с традиционного определения понятия "твердость": "Обычно тело считают твердым, если его части, оставаясь в покое одна относительно другой, таковы, что их связи могут быть разрушены лишь какой-либо внешней силой, и считают, что эта твердость тем более совершенна, чем большую силу необходимо применить, чтобы отделить части этого тела друг от друга. В соответствии с этим понятием, тело будет совершенно твердым, в смысле абсолютного совершенства, когда его части не смогут быть разделены никаким конечным усилием, каким бы большим мы это усилие ни предположили" [1, c. 157].

Но И. Бернулли не может принять такое определение, считая его нереальным. Он называет его химерой, противоречащей основному закону природы – "закону непрерывности, в силу которого все, что выполняется, выполняется через бесконечно малые изменения. Здравый смысл, кажется, диктует то, что никакое изменение не может осуществляться скачками: Natura non operatur per saltum, ничто не может перейти от одной крайности к другой, не переходя через все промежуточные ступени" [1, c. 157]. Мысль о том, что "Природа ничего не делает скачком" была одним из основных положений философии Лейбница.

Реальные тела не могут отвечать требованиям "совершенной твердости", они разрушаемы, деформируемы. Но их разрушение не является мгновенным, скачкообразным, оно является непрерывной последовательностью стадий, протекающих некоторое (пусть малое!) время. Поэтому все твердые тела по своим физическим свойствам ассоциируются с телами деформируемыми (мяч, наполненный воздухом; пружина).

В итоге автор приходит к следующему определению: "...тело будет твердым..., если его чувственные части с трудом меняют свое положение и если части этого тела, сдвинутые вследствие удара другого тела, в незаметный промежуток времени очень быстрой и упругой пружинистостью приводятся в свое первоначальное положение. Эта упругость совершенна, если все сдвинутые части восстанавливают свое первоначальное состояние; она несовершенна, если некоторые из них в него не возвращаются. Совершенную упругость можно назвать тугостью" [1, c. 157]. Таким образом, понятию "совершенной твердо- сти" соответствует "бесконечная тугость", по Бернулли ("...тело будет бесконечно тугое, если нужно бесконечное давление для конечного сжатия этого тела или если нужно конечное давление для бесконечно малого сжатия его" [1, c. 157]).

В основу теории передачи движения И. Бернулли полагает законы инерции и равенства действия – противодействия абсолютно упругих тел. Обсуждая физическую сущность соударения тел, он предлагает модель трубки, закрытой с одного конца, внутри которой перемещается поршень. Перемещение поршня под действием внешней силы (удара) приводит к увеличению внутреннего давления воздуха, гасящего удар по поршню и далее возвращающего поршень в начальное положение. Это своеобразный аналог пружины, упругие свойства которой определяются ее геометрическими размерами (длиной). И сила пружины по своему действию аналогична силе веса.

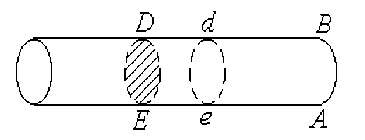
Рис. 3

Опыты показали, что упругость воздуха пропорциональна его плотности. Для трубки постоянного диаметра это означает, что сила упругости воздуха обратно пропорциональна длине eA = x (рис. 3).

Пользуясь законом  du = Fdt, где dx                           1 dx dt = —, Бернулли получает du =--или u                       x и dx udu = — и далее интегрирует это диффе-x ренциальное уравнение с учетом начальных условий. Обратим внимание на то, что полученное выражение устанавливает пропорциональность живой силы активной силе и является, говоря современным языком, аналогом теоремы об изменении кинетической энергии.

Поведение поршня в трубке фактически является моделью движения снаряда в стволе пушки. Это обстоятельство позволяет Бернулли дать несколько полезных рекомендаций по поводу свойств пороха и оптимальной длины ствола для получения наибольшей скорости снаряда в момент его вылета.

В третьей главе работы вводятся основные понятия и принцип равновесия, впервые сформулированный автором в письме Вари-ньону (26 января 1717 г.) и получивший позднее высокую похвалу Лагранжа.

" Определение I . Виртуальной скоростью я называю ту скорость, которую приобретают две или несколько сил, находящихся в равновесии, когда им сообщают небольшое движение. Или, если эти силы уже находятся в движении, то виртуальная скорость есть элемент скорости, на который увеличивается или уменьшается скорость каждого тела, за бесконечно малое время, если считать направление этого элемента совпадающим с направлением скорости" [1, c. 158].

Понятие виртуальной скорости является одним из основных в современной аналитической механике. Оно формировалось на протяжении всей истории механики, но впервые получило четкое определение в работах Бернулли. В уже упомянутом письме Вариньону он пишет: "Представьте себе несколько различных сил, которые действуют по различным направлениям, чтобы держать в равновесии точку, линию, поверхность или тело; представьте также, что всей системе этих сил сообщают малое движение или параллельно самой себе по какому-нибудь направлению, или же вокруг какой-нибудь неподвижной точки. Вам будет легко понять, что при этом движении каждая из сил продвинется или отступит по своему направлению, за исключением тех, которые направлены перпендикулярно к направлению малого движения. В этом последнем случае эти одна или несколько сил не продвинутся вперед и не отступят назад, так как эти продвижения или отступления, называемые мною виртуальными скоростями, суть не что иное, как то, на что увеличивается или уменьшается линия направления каждой силы при этом малом движении; эти увеличения или уменьшения можно определить, если из конца линии направления какой-либо силы опустить перпендикуляр на линию направления, взятую в соседнем ее положении после малого движения, на которой он (перпендикуляр) отсечет маленькую часть, которая и будет мерой виртуальной скорости этой силы" [1 с. 159]. Эта конкретизация понятия виртуальной скорости ясно показывает и представление Бернулли о силе как о направленном отрезке ("линия направления"), произведение которого на виртуальную ско- рость характеризует состояние тела. Эта характеристика названа им "энергией".

Дав определения живой силы ("...та сила, которая пребывает в равномерно движущемся теле") и мертвой силы ("...та, которую получает тело без движения, если оно побуждается и принуждается к движению, или же, которая побуждает двигаться быстрее или медленнее, если тело уже находится в движении"), автор формулирует основной принцип: "Два фактора находятся в равновесии, то есть имеют равные моменты, когда их абсолютные силы находятся в обратном отношении к своим виртуальным скоростям, - безразлично, находятся ли действующие одна на другую силы в движении или в покое" [1, с. 159]. По сути, этот принцип - прообраз общего уравнения динамики, сформулированного Лагранжем через 60 лет.

Отметим, что требование равномерности движения в определении живой силы не является обременительным, так как речь идет о бесконечно малом движении, фактически о мгновенной скорости. Бернулли утверждает, что "это - обычный принцип статики и механики", поэтому он не нуждается в доказательствах. Однако следует иметь в виду, что этот старейший принцип ранее применялся для изучения только равновесия тел. Но, возможно, именно этот принцип навел Декарта на мысль о законе сохранения количества движения, подтверждающем всеобщность принципа. Для Бернулли же закон Декарта является следствием общего принципа.

Исходя из галилеевых законов падения тел, Лейбниц установил, что живая сила тела равна произведению его массы на квадрат скорости. Бернулли приходит к такому же выводу исходя из других соображений. Если рассмотреть взаимодействие двух тел А и В, соединенных пружиной (это его модель взаимодействия), то центр тяжести С тел А и В всегда будет покоиться. Это означает, что "живая сила тела В (А) является полным результатом действия части СВ (СА) пружины". Результат же действия пружины пропорционален ее удлинению (длине). Если обозначить f (F) - живую силу тела А (В), a (b) - скорость тела А (В), то f  CA  CAa

— = —; — = —.

F  CB CBb

Из закона сохранения количества движения aA = bB (массу тела А (В) Бернулли, как это было общепринято, ассоциирует с самим телом).

В таком случае f   a aA  Aa2

— = —--=--— .

F  b bB  Bb ²

После введения меры живой силы как произведения массы на квадрат скорости подробно обсуждаются природа и свойства живых сил, способы их измерения, приводится аналог теоремы об изменении кинетической энергии, который используется как метод решения задач, но не объявляется в качестве возможного принципа механики.

Законы соударения тел (определения скоростей после удара) Бернулли получает, основываясь на идее относительности движения в стиле Гюйгенса. Для этого он добавляет достаточно очевидную аксиому ("предложение II") о том, что относительные движения тел в результате удара не зависят от движения плоскости, в которой происходит удар (движение). При этом вводится понятие "количество направления", позднее вошедшее в механику как "количество движения центра масс". Полученные результаты, по мнению автора, обобщают результаты Гюйгенса в теории удара.

Современное понятие кинетической энергии тела по своей математической форме мало чем отличается от понятия живой силы. Поэтому история формирования понятия живой силы, трансформация его физического содержания не просто любопытна, а является способом освоения понятия кинетической энергии, его роли в современном понимании природы и описании движения тел. Бернулли указывает, что мертвая сила оказывает давление, она производит движение или вызывает "сопротивление препятствия", называемое ныне реакцией связи. Эта реакция связи всегда равна и противоположна действующей силе.

Примерами мертвой силы являются силы тяжести, упругости пружины.

Природа живой силы совершенно иная. Эта сила возникает и исчезает не мгновенно, а за некоторое время; она непрерывно производится в теле и может в нем сохраняться после прекращения действия вызвавшей ее причины; "она эквивалентна той части причины, которая израсходовалась, производя ее, ибо всякая действующая причина должна быть равна своему действию, полностью выполненному. Тело, получающее эту силу, если оно не задерживается никаким препятствием, не оказывает никакого противодействия этой силе за исключением того, которое зависит от инерции, всегда пропорциональной массе; ...по мере того как тело воспринимает новые доли силы, причина их производящая должна их в той же степени терять… Именно эту силу, передаваемую телу, приведенному в движение посредством истощения давления пружины, и нужно называть собственно "живой силой". Благодаря ей тело и переносится с одного места в другое с известной скоростью, большей или меньшей в соответствии с энергией пружины" [1, c. 161]. А далее автор добавляет, что живая сила может быть израсходована на производство мертвой силы, например, на сжатие пружины. И величина ее сжатия будет равна той, которая была нужна для получения этой живой силы.

Обращаясь к вопросу о математическом выражении живой силы, И. Бернулли, используя второй закон Ньютона, получает выражения

1    u 2 = I pdx, udu = pdx где p – сила действия пружины, x – ее деформации, v– скорость поршня.

Сравнение и измерение живых сил Бернулли сводит к сравнению и измерению упругих сил соответствующих пружин – сил, пропорциональных удлинению пружин.

Далее автор приводит теоретические следствия и экспериментальные доказательства полученных результатов. Он рассматривает случаи абсолютно неупругого удара шара и поверхности, абсолютно упругого косого удара двух шаров, удары шаров о пружины.

Возвращаясь к законам прямого удара абсолютно упругих тел, Бернулли демонстрирует как из закона сохранения количества движения до и после удара получить соответствующий закон сохранения живых сил, впервые установленный, но не осознанный Гюйгенсом. Он предлагает считать эти законы единым законом, имеющим разные математические выражения. По-видимому, именно так отнесся к ним Гюйгенс, не придав своему равенству статуса нового закона сохранения – сохранения живой силы как основной меры движения. Для Бернулли законы сохранения, как математический, теоретический аналог философского закона равенства действующих причин и их результатов, являются залогом стабильности природы, ее порядка.

Эта мысль чрезвычайно важна для статуса законов сохранения (как основополагающих принципов теории и методов решения задач) в последовательном развитии физики и теоретической механики.

Задачу о движении тела в среде Бернулли сводит к задаче об ударе одним телом нескольких (системы) тел, представляя среду как множество шариков-молекул (отождествляет силу сопротивления среды с суммарной силой последовательных ударов тела о шарики-молекулы). Решение приводит автора к следующим результатам: предлагаемая теория позволяет определить "абсолютные действия сопротивления среды"; среда "оказывает движущимся в ней телам сопротивление, пропорциональное квадратам их скоростей"; "можно найти средство точно определить, сколько в действительности тело... потеряет в своей скорости после того, как им будет пройдено данное расстояние"; "исследование этого нового вопроса столь же любопытно, сколь и полезно на практике. Оно может привести к законам различных явлений, и тем достойнее было бы в него углубиться, что никто еще этим не занимался"; "величина потери скорости зависит и от формы движущегося тела" и от отношения плотности тела к плотности среды. Сделанные выводы используются для получения расчетных данных движения в воздухе свинцовой пули (коноида), куба, прямого конуса. Выводится закон движения тела по траектории для случая квадратичного закона сопротивления, определяются кривые остаточных скоростей и времен. Задача обобщается для случая сопротивления среды пропорционального произвольной степени скорости.

Последняя глава книги называется "Новый способ определения центра качания сложного маятника при помощи теории живых сил...". Задача об определении центра качания физического маятника, сформулированная в первой половине XVII столетия и привлекшая внимание всех видных механиков, наряду с задачами о падении тяжелых тел и ударе стала своеобразным полигоном для формулировки новых принципов механики и проверки – эффективности новых методов решения задач. Поэтому обращение И. Бернулли к этой задаче было вполне естественным. Используя принцип сохранения живых сил, И. Бернулли повторяет результат, полученный ранее его братом.

Продолжением "Рассуждения о законах передачи движения" стала работа И. Бернулли

"Об истинном значении живых сил и их применении в динамике", где уточняется понятие живой силы: "Живая сила состоит не в действительной работе, а в способности к действию: она существует и тогда, когда не действует и когда не имеет объекта, на который она могла бы действовать. Так, например, натянутая пружина или же, скажем, тело с установившимся движением имеют в себе способность к действию, хотя бы вне их и не было ничего такого, на чем они могли бы проявить эту способность..." [1, c. 168]. Он считает, что живую силу "лучше было бы называть "способностью к действию", вкладывая в нее энергетический, потенциальный смысл. Из живой силы "ничего не может пропасть без того, чтобы мы снова не нашли эту потерю в произведенном действии; ...живая сила всегда сохраняется..., находившаяся до действия в одном или нескольких телах..., после действия обязательно встретится нам в другом теле или в других нескольких телах, если только она не останется неизменной в прежних телах. Это и есть то, что мы называем сохранением живых сил" [1, c. 168].

Дальнейшее обращение Бернулли к идее сохранения живых сил показывает, что сохранение полной механической энергии тел было осознано им не только на физическом уровне, но и получило свое математическое воплощение: PdS = VdV , где P – "ускорительная сила", dS – элемент пройденного пути, V – скорость. Записанное уравнение автор использует для решения нескольких задач и называет очень распространенным принципом динамики, "в правильности которого никто не сомневается". Этот принцип далее используется для доказательства уже упоминавшегося принципа Торричелли–Роберваля–Гюйгенса о высоте центра тяжести системы тел: "В настоящее время я полагаю, что истинность этой аксиомы Гюйгенса доказана и подкреплена теорией живых сил, так что на будущее время она законно должна занять место среди тех предложений динамики, которые считаются наиболее достоверными" [1, c. 168].

К задаче о брахистохроне И. Бернулли возвращался многократно. Искал новые решения, ставил вопрос о единственности решения. Так, в "Мемуарах Парижской академии наук" за 1706 г. вышла работа "Решение задачи... об изопериметрических", посвященная решению задачи (1697) Я. Бернулли, которая стала примером классической постановки вариационной задачи.

В августе 1697 г. в "Journal des Sçavans" он опубликовал постановку еще одной экстремальной задачи, обсуждавшейся им в переписке с Лейбницем, – о геодезических линиях: найти кратчайшую траекторию между точками на выпуклой поверхности. Задача оказалась непростой. Бернулли опубликовал свое решение только в 1742 г., хотя основная идея метода была высказана в письме Лейбницу в 1715 г. Первым же решение этой задачи опубликовал Эйлер ("Комментарии Петербургской академии наук", 1732).

В процессе решения этой задачи И. Бернулли ввел понятия пространственных координат и уравнения поверхности: "Под данной кривой поверхностью я разумею такую, отдельные точки которой (подобно точкам данной кривой линии) определяются тремя ординатами x , y , z , отношение между которыми выражается данным уравнением; эти же три координаты суть не что иное, как три перпендикулярных отрезка, проведенных из какой-либо точки поверхности к трем плоскостям, данным по положению и взаимно пересекающимся под прямыми углами" [1, c. 172].

За прожитые 80 лет И. Бернулли внес значительный вклад в развитие новой механики и ее практических приложений (принцип сохранения живых сил, теория удара, внутренняя и внешняя баллистика, гидравлика, теория корабля, ввел обозначение g для ускорения свободного падения).

Особо следует отметить вклад И. Бернулли в формулировку принципа виртуальных скоростей и в формирование современного понятия кинетической энергии (само понятие и термин появились только в XIX веке) – одной из основных мер движения в теоретической механике.

Однако трудно дать объективную оценку заслуг И. Бернулли в механике, не обращаясь к его математическому творчеству. Специфика теоретической механики состоит в том, что математические приемы решения задач, математический аппарат механики не есть нечто внешнее для механики, а являются ее составной частью. Поэтому многие работы Бернулли-математика по своей сути имеют механическую направленность.

Это были работы, закладывавшие основы дифференциального и интегрального исчисления (ему принадлежит первое изложение исчисления), теории дифференциальных уравнений, вариационного исчисления, аналитической геометрии (в 1715 г. он дал определение пространственных координат). И. Бернулли развил теорию показательных функций, вывел правило раскрытия неопределенностей типа 0/0 (носящее имя Лопиталя), разработал методы интегрирования рациональных дробей, вычисления площадей плоских фигур, спрямления некоторых кривых, открыл ряд, родственный ряду Тейлора, дал определение функции как аналитического выражения, составленного из переменных и постоянных величин.

Его работы вызывали живой отклик не только современников, но и ученых следующих поколений. Он сформировал начальный круг научных интересов Леонарда Эйлера, своих сыновей Даниила и Николая. Даламбер считал, что своим знанием математики и механики он обязан И. Бернулли. В первой половине XVIII в. Иоганн Бернулли был одним из самых авторитетных математиков Европы.