О некоторых свойствах n-последовательносвязной цепи

Пусть G = (J,E ) — неориентированный граф с множеством вершин J и множеством ребер E . Пусть N(j ) - множество вершин графа G = (J,E ), смежных с вершиной j . Пусть 97(G) - плотность графа G. Далее будем предполагать, что на множестве вершин J введена нумерация и каждая вершина отождествлена с присвоенным ей номером.

Определение 1. Связный граф G = (J,E ) называется n-последовательносвязной цепью (n-sequential ly connected chain), если на множестве его вершин можно задать такую нумерацию, что для любой вершины графа G с номером j , имеет место включение

N^{( j} ) С ^{{ ( j} — n),..., ^{( j} — 1), ^{( j} + 1),..., ^{( j} + n ^{) }} : n = y ⁽ G) — 1.

В дальнейшем такие вершины i и k будем именовать крайними вершинами n-последовательносвязной цепи. Заметим, что такие вершины i и k будут симплициальные.

На рис. 1 для различных n представлены n-последовательносвязные цепи.

Рис. 1.  n-последовательносвязные  цепи:     a) 1-последовательносвязная цепь;

b) 2-последовательносвязная цепь; c) 3-последовательносвязная цепь

То есть 1-последовательносвязная цепь представляет собой простую цепь, т.к. для любых j | N (j) | <  2 и каждая вершина такой цепи связана не более чем с одной предшествующей вершиной. В 2(3)-последовательносвязной цепи каждая вершина связана не более чем с двумя (тремя) предыдущими вершинами соответственно.

На данный момент можно выделить два основных направления использования n-последовательносвязных цепей.

Первое – задачи размещения, в частности, задача Вебера в дискретной постановке [1], так как структура некоторых производственных процессов представляет собой n-последовательносвязную цепь. Например, в работе [2] предложен точный квази-полиномиальный алгоритм для решения задачи Вебера для неориентированной n-последовательносвязной цепи и конечного дискретного множества мест размещения.

Второе направление – решение задач выбора оптимального поведения в системах, описываемых управляемыми марковскими процессами, когда цепь Маркова является n-сложной, так как структура n-сложной марковской цепи представляет собой n-последовательносвязную цепь.

Основные характеристики и свойства n -последовательносвязной цепи

Приведем характеристики п-последовательносвязной цепи G = (J, E ).

• 1.    Число ребер графа G равно:

  о чⁿ ;■))■

  
  

• 2.    Размер максимальной клики графа G равен п + 1, причем существует | J | — п таких максимальных клик;

• 3.    Граф G имеет 2 симплициальные вершины;

• 4.    Число вершинной связности ξ G графа G равно n , т.е. любая n -последовательно-связная цепь является n -связным графом;

• 5.    Хроматическое число X G графа G равно п + 1;

• 6.    Цикломатическое число C G графа G равно:

| E I = ( I J I — п) • n + ^ (п — i) = ( I J I — п) • n + n 2 n = n i=1,n

Cg = п • (и — (^-2^)) — I J | +1 = ( | J I — п — 1) • (п — 1).

Рассмотрим некоторые свойства п-последовательносвязной цепи G = (J,E ).

Теорема 1. В п-последовательносвязной цепи G = (J,E) ни один из порожденных подграфов не является простым циклом длины l >  4 .

Доказательство. В пронумерованной п-последовательносвязной цепи G = (J, E ) рассмотрим две цепи L i = ( Jli,Eli ) и L 2 = ( Jl2,El2 ) , номера вершин которых принадлежат множествам N L1 и N L2 соответственно, причем

m

NL1 = {j,j + ki,j + ki + k2,--,j + ^ki}, i=1

где j E { 1, 2,..., | Jli |} и для любых i = 1, 2,..., m целые числа k i E { 1, 2,..., п } , при том, что j + E m=i k i < I Jli I ;

w

NL2 = {j",j" - hi,j" - hi - h2, •••,j" - E ht, j}, t=i где j" = j + Ei=Tm ki и Для любых t = 1,2, ..., w целые числа ht E {1, 2, ..., n}, при том, что j - EW=i ht > j. Пусть L = Li U L2 — простой цикл длины m + w + 1 > 4.

Пусть некоторая вершина цепи L 2 с номером j " - Et =i h t , где ^ E { 1, 2, ..., w } , находится «между» вершинами цепи L i с номерами j + E p=i k i и j + E P="i k i , где P E { 1, 2, ..., m } и k p +i >  2. Очевидно, что

• p           w         p+i

j + E k i h t i =i             t =i            i =i

Для такой вершины цепи L 2 с номером j" - Et =i h t найдется хотя бы одно ребро (хорда) (j + E iE k i , j" - E tE h t ) E E либо (j" - E t=_i h t , j + EE k i ) E E, которое не принадлежит множествам ребер цепей L i и L 2 , т. к. цикл L = L i U L 2 по определению простой и

(Vj E {1, 2, •••, | J|}) N(j) C {(j - n), ••, (j - 1), (j + 1), ••, (j + n)}, и для любых i E {1, 2,..., m} и t E {1, 2,..., w} справедливо неравенство 1 < ki, ht < n. Исходя из этого, в графе G ни один из порожденных подграфов не является простым циклом длины l > 4. Теорема 1 доказана.                                                               □

Использованные в доказательстве теоремы 1 простые цепи L i и L 2 , а так же хорды, соединяющие несмежные вершины простого цикла L в 3-последовательносвязной цепи представлены на рис. 2.

Рис. 2. bsd

Исходя из теоремы 1 n-последовательносвязная цепь при любых значениях параметра n является триангулированным (хордальным) графом [3–6]. Несмотря на справедливость теоремы 1 имеют место следующие свойства n-последовательносвязной цепи.

Теорема 2. В n-последовательносвязной цепи G = (J, E) при n > 2 с количеством вершин | J | >  2n + 1 существует порожденный подграф, являющийся циклом длины l >  4 .

Доказательство. Для доказательства теоремы 2 необходимо и достаточно найти в графе G такой цикл L длины l >  4, для которого в графе G не существует ребра соединяющего две несмежные вершины цикла L.

Пусть L = ( Jl , El ) ^: | El | >  4 цикл в графе G, номера вершин которого принадлежат множеству N L , причем

Nl = {j, j + n,j + 2n, •••j + kn, j + kn - 1, j + (k - 1)n, j + (k - 1)n - 1,j + (k - 2)n, •••j}, при условии, что целое число к = 2, 3,..., при том, что j + kn < | Jl |.

Очевидно, что для любой вершины l G Jl не существует таких ребер (l, m) G E : m G Jl , которые бы не принадлежали множеству ребер E L цикла L, так как известно, что для любых j G { 1, 2,..., | J |} множество N(j ) C { (j — n),.., (j — 1), (j+1),.., (j+n) } . Теорема 2 доказана. □

Такой цикл L в n-последовательносвязной цепи при n = 3,4 представлен на рис. 3.

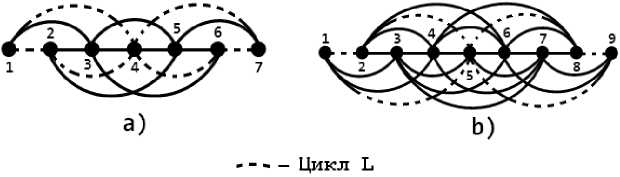
Рис. 3. csd

Теорема 3. В любой n-последовательносвязной цепи G = (J, E) при n >  4 существует порожденный подграф, являющийся циклом длины l >  4 .

Доказательство. Положим, что A = ( Ja,Ea ) - подграф n-последовательносвязной цепи G = (J, E ) при n >  4, образующий клику размера к + 1, где 4 <  к <  n : k(mod 2) = 2.

Так как степени всех вершин такой клики A четны, то подграф M индуцированный множеством вершин клики A является эйлеровым графом, а значит найдется такой цикл L = M , который включает в себя все вершины и ребра порожденного графа M G G.

Исходя из этого, в графе G существует порожденный подграф L, являющийся циклом длины l >  4. Теорема 3 доказана.                                                     □

Несмотря на справедливость теорем 2 и 3 имеет место следующая теорема.

Теорема 4. В n-последовательносвязной цепи G = (J, E) при n = 2 ни один из порожденных подграфов не является циклом длины l >  4 .

Доказательство. Пусть L = ( Jl , El ) : | El | >  4-циклвграфе G, где Jl = { j, i i , i 2 ,..., i t , j } : j ∈ J.

Рассмотрим два случая цикла L : первый случай – когда вершина i 1 есть вершина с номером j + 1, второй случай - когда вершина i 1 есть вершина с номером j + 2.

Рассмотрим первый вариант первого случая цикла L , когда

JL = {j,j + 1^2,-Л ,j',j + 1,j — Mr+4, -litd} : j' G {j + 2,j +3}.

В данном варианте при любых j ' G { j + 2, j + 3 } в графе G имеется ребро (j,j + 2) G E , соединяющее две несмежные вершины цикла L (рис. 4, a – b), т.к. вершина с номером j +2 при любых j содержится в цикле L и цикл заканчивается в вершине с номером j. В дальнейшем такое ребро будем называть хордой.

Во втором варианте первого случая цикла L вершина it = j + 2. Здесь, в свою очередь, возможны два случая: первый, когда i2 = j + 3 - с хордой (j + 1, j + 2) G E, т.к. для любых it-i G {j + 3, j + 4} ребро (j + 1, j +2) G E не принадлежит циклу L (рис. 4, c), второй, когда i2 = j + 2 и i3 G {j + 3, j + 4} - с хордой (j + 1, j + 3) 6 E, т.к. при i3 = j + 3 вершина it-1 = j + 4, а при i3 = j +4 вершина it-i = j + 3 и во всех случаях ребро (j + 1, j + 3) G E не принадлежит циклу L (рис. 4, d – e).

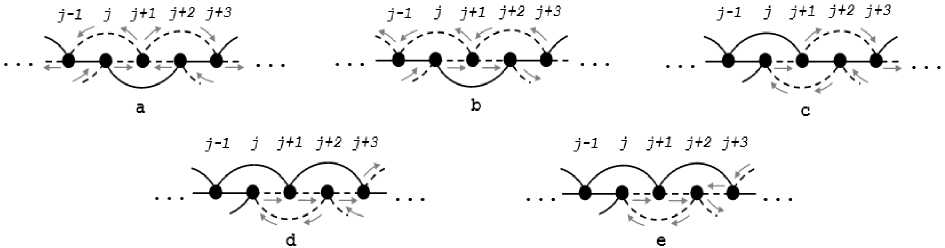
Рис. 4. Первый вариант построения цикла L в 2-последовательносвязной цепи Рассмотрим первый вариант второго случая цикла L , когда

J L = ^{{ j,j +2 ,}i 2 , -Vir ^{,j +3 ,j + 1 ,j /} ,i r+4 , ...,i t ,^{j } :} j ^{G { j,j - 1 }} .

В данном варианте при j ' = j — 1 в графе G содержатся две хорды (j, j + 1) G E и (j + 1, j + 2) G E (рис. 5, a), а при j ' = j - хорда (j + 1, j +2) G E (рис. 5, b).

Во втором варианте второго случая цикла L , когда

JL = {j,j +2,i2, ...,ir,j +2,j + 1,j/,ir+4, ...,it,j} : j' G {j,j — 1}, при j' = j — 1 в графе G содержится хорда (j,j + 1) G E (рис. 5, c), а при j' = j, когда i2 G {j + 3, j +4} - хорда (j + 1, j + 3) G E (рис. 5, d - e).

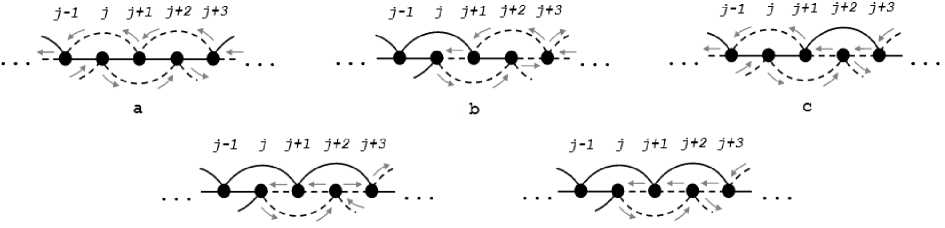
d                                       e

Рис. 5. Второй вариант построения цикла L в 2-последовательносвязной цепи

Так как цикл L во всех возможных случаях содержит хорду, то в n-последовательносвязной цепи G = (J, E) при n = 2 ни один из порожденных подграфов не является циклом длины l >  4. Теорема 4 доказана.                         □

Так как согласно теореме 1 любая n -последовательносвязная цепь является триангулированным графом, свойства n -последовательносвязной цепи повторяют свойства хордального графа. В частности справедливы

Свойство 1. Любая n -последовательносвязная цепь является совершенным графом.

Свойство 2. Любое разделяющее множество вершин n -последовательносвязной цепи, минимальное относительно включения, есть клика.

Свойство 3. Если n-последовательносвязная цепь отлична от полного графа, то в ней имеется две симплициальные вершины.

Свойство 4. Каждая часть n-последовательносвязной цепи относительно разделяющего множества вершин, являющегося кликой – совершенный граф.

Свойство 5. Неориентированная n-последовательносвязная цепь имеет дерево клик, причем древовидная ширина n-последовательносвязной цепи равна n + 1.

Отношение класса n-последовательносвязных цепей к другим классам графов представлено графически на рисунке 6.

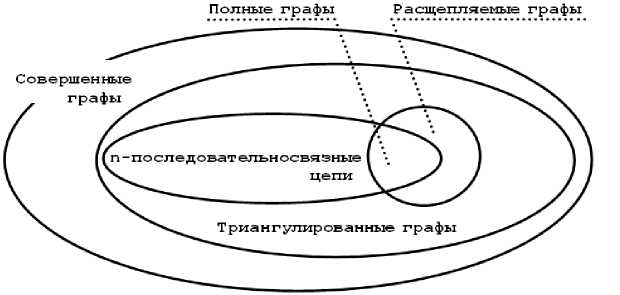
Рис. 6. Отношения классов графов

Т.е. класс n-последовательносвязных цепей принадлежит классам совершенных и триангулированных графов, при том, что n-последовательносвязные цепи с числом вершин | J | = n + 1 принадлежат классу полных графов, а n-последовательносвязные цепи с числом вершин | J | = n + 2 - классу расщепляемых графов.

Заключение

В работе введено понятие неориентированной n-последовательносвязной цепи. Обозначены области применения n-последовательносвязных цепей. Рассмотрены основные характеристики n-последовательносвязной цепи.

Доказано, что в n-последовательносвязной цепи при любых значениях параметра n ни один из порожденных подграфов не является простым циклом длины l >  4, из чего следует, что класс n-последовательносвязных цепей принадлежит классу триангулированных графов.

Так же доказано, что в n-последовательносвязной цепи при n >  2 с количеством вершин | J | >  2n + 1 ив любой n-последовательносвязной цепи при n >  4 существует порожденный подграф, являющийся циклом длины l >  4, при том, что в n-последовательносвязной цепи при n = 2 ни один из порожденных подграфов не является циклом длины l >  4.

Определено отношение класса n-последовательносвязных цепей к классам совершенных, триангулированных, полных и расщепляемых графов.