О нелокальном использовании результатов локального анализа динамических систем

В настоящее время при построении законов движения динамических систем [1], т. е. при решении задачи Коши («начальная» задача) [2, 3] или при построении периодического решения [3] дифференциальных уравнений движения динамических систем, как правило, авторы используют «численное» решение. При этом анализируется лишь одна точка пространства параметров динамической системы. Однако в завершении исследования, никак это не обосновывая, авторы пытаются обобщить полученные выводы на всё пространство параметров динамической системы. В общем случае это, конечно же, недопустимо. Такой переход к «нелокальному использованию результатов локального анализа» возможен лишь в том случае, когда исследуемая динамическая система обладает некоторыми специальными свойствами [4].

Поскольку данная проблема общеизвестна [4] и возникает всякий раз при «численном» построении законов движения динамических систем, т. е. несомненно актуальна, рассмотрим более подробно ее решение на примере построения законов движения автомобиля с адаптивной подвеской по непрямолинейному профилю дорожного покрытия.

• 1 . Расчетная схема автомобиля с адаптивной подвеской, принятые допущения

Итак, рассмотрим динамическую модель переднеприводного автомобиля с адаптивной подвеской [5], движущегося по непрямолинейному дорожному покрытию (см. рисунок).

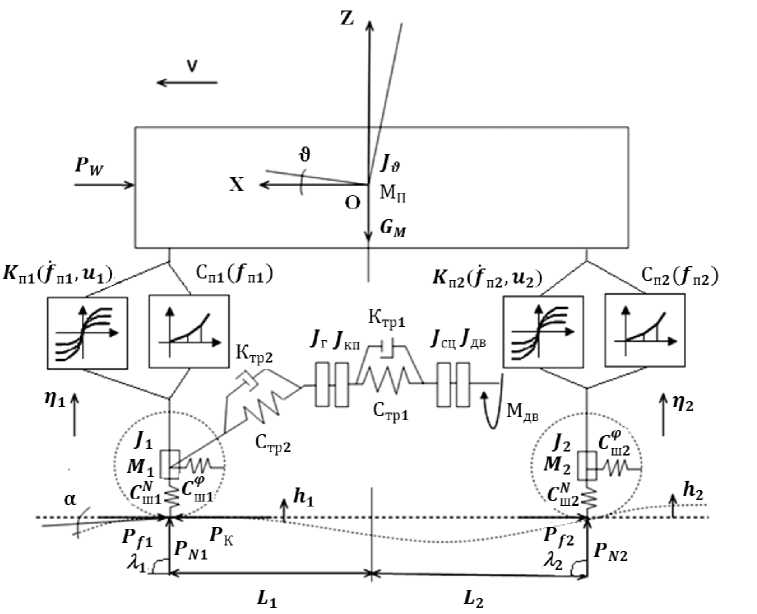
Расчетная схема транспортного средства с адаптивной подвеской

На рисунке введены следующие обозначения: J ДВ - маховик, имитирующий вращающиеся детали и звенья приводного двигателя; J СЦ - маховик, имитирующий вращающиеся детали диска сцепления и приведенные к нему ведущие звенья коробки передач; J КП - маховик, имитирующий вращающиеся детали ведомых звеньев коробки передач; J Г - маховик, имитирующий вращающиеся детали от синхронизатора включенной передачи до их колес автомобиля; С П1 (f П1 ), С П2 (f П2 ) - функциональные аналоги упругих элементов с нелинейной рабочей характеристикой передней и задней подвесок, соответственно; K П1 (f П1, u 1 ), K П2 (f П2 , u 2 ) - функциональные аналоги адаптивных амортизаторов передней и задней подвесок соответственно; f П1 , f П2 - деформация передней и задней подвески соответственно; u 1 , u 2 - управляющие воздействия на адаптивные амортизаторы передней и задней подвески соответственно; С ТР1 , С ТР2 , K ТР1 , K ТР2 - коэффициенты жесткости и демпфирования соответствующих участков трансмиссии; C^N ш1 , C^N ш2 , C ^ϕш1 , C ^ϕш2 - коэффициенты нормальной и угловой жесткости шин колес передней и задней осей соответственно; α - угол спуска                                                                                    (подъема);

ϑ - угол поворота подрессоренной массы в плоскости XOZ ; M П - масса подрессоренная; М 1 , М 2 - массы неподрессоренные, передняя и задняя соответственно; η 1 , η 2 - перемещения вертикальные соответствующих неподрессоренных масс; h 1 , h 2 - высота неровностей дорожного профиля под соответствующими колесами; P k - сила тяги; P f1 , P f2 - силы сопротивления качению соответствующих колес; P N1 , P N2 - реакции нормальные соответствующих колес; λ 1 , λ 2 - углы наклона нормальных реакций; P W - сила сопротивления воздуха.

При составлении динамической модели автомобиля приняты следующие допущения:

• –    движение плоское (в поперечной плоскости движение отсутствует), т. е. высота неровностей дороги под левыми и правыми бортами одинаковая и перемещение неподрессоренных масс

происходит только перпендикулярно плоскости дороги, в продольном направлении вместе с подрессоренной массой;

• –    рассматриваются легковые автомобили среднего класса сегмента B длиной до 4,2 м;

• –    рассматриваются переднеприводные автомобили;

• –    проскальзывание в точке контакта колеса с опорной поверхностью отсутствует;

• –    не учитывается диссипация энергии в пружинах подвески, сайлентблоках и т. п.;

• –    не учитывается деформация сайлентблоков и подобных элементов подвески.

• 2 . Математическая модель транспортного средства с адаптивной подвеской

При разработке динамической модели за основу была взята модель, предложенная авторами В.А. Умняшкиным, Н.М. Филькиным, Р.С. Музафаровым [6]. Новизна нашей модели заключается в рассмотрении переднеприводного автомобиля с адаптивной подвеской, а также наличии разработанных функциональных аналогов упругих элементов с нелинейной рабочей характеристикой и адаптивных амортизаторов, характеризующихся семейством нелинейных рабочих характеристик, математическое описание которых представляет собой функцию двух переменных - скорости перемещения штока и управляющего параметра.

С учетом принятых допущений исследуемая динамическая система имеет десять степеней свободы. Запишем вектор обобщенных координат:

q= COI{X Z ^fl ^ 1    ф^ ф^ ф^ ф г ф к J.

Здесь: X - продольное перемещение автомобиля; Z - перемещение подрессоренной массы вертикальное; ϑ - угол поворота подрессоренной массы в плоскости XOZ ; η 1 , η 2 - перемещения вертикальные соответствующих неподрессоренных масс; ϕ дв , ϕ сц , ϕ кп , ϕ г - углы поворота деталей соответствующих участков трансмиссии.

Следует отметить, что исследуемая динамическая система содержит неголономные связи. Поэтому составление математической модели движения автомобиля на основе уравнений Лагранжа второго рода в данном случае неприемлемо. Для составления математической модели движения исследуемой динамической системы воспользуемся особой формой уравнений Лагранжа второго рода – уравнениями Лагранжа второго рода с избыточными координатами [7]:

d фТТ \ ФТ , дП , ФФ _А    V ₂ , ,

• “ ад^ )^- д^ ⁺ д^ ⁺ д^ ^-^ ⁺ ^=^{1 Я}^                               (1)

Здесь: Т – кинетическая энергия системы; П – потенциальная энергия системы; Ф – диссипативная функция Рэлея, характеризующая скорость рассеяния механической энергии; Q k – обобщенная сила, соответствующая к -й обобщенной координате q_k; q - оператор - оператор дифференцирования по переменной t ; A - множители Лагранжа [10]; h_ik - дополнительные функции «Лагранжа»; k ∈ {1, 2, …, 12}.

Избыточные координаты не являются независимыми. Поэтому к уравнениям (1) следует добавить уравнения, связывающие избыточные координаты с независимыми обобщенными коор- динатами:

d^ Nl = 0; ^dX N2 dt ; dt .

Здесь: “d ^¹ , ^d ^ ² - проекции векторов скоростей точек N 1 и N 2 на ось OX .

Рабочий режим движения исследуемой динамической системы – переходный процесс, пред- ставляющий собой «наезд автомобиля на неровность и последующий её проезд». В математической постановке реализация этого процесса [8–11] соответствует решению задачи Коши с задан- ными начальными условиями:

Х(О)=Х о ; Z(O)=Z o ; fl(0) - fl₀; ^ i (0) - ^1_O; ^ 2 (0) - ^2₀;

ϕ д_в (0)= ϕ д_в0 ; ϕ _сц (0) = ϕ _сц0 ; ϕ _кп (0)= ϕ _кп0 ;                                                           (3)

ϕ 2 (0)= ϕ 20 ; ϕ k1 (0)= ϕ k10 .

Для использования в математической модели движения автомобиля [12–14] разработанных функциональных аналогов упругих элементов и регулируемых амортизаторов необходимо вычислить частные производные потенциальной энергии П и диссипативной функции Ф системы по обобщенным координатам и скоростям. Вычисление частной производной слагаемых потенциальной энергии системы, связанных с упругими элементами подвесок, по обобщенным координатам проводится по соотношению

а( П п 1 + П п ₂ )   _ - Р ^п Чп 1 (f M^g^df, 1 . d$ Q ^{п 2}С п ₂(f n ₂(Z,V^ _{V 2}))df n ₂

dq                    dq                          dq           "

Деформация упругих элементов С_п1 , С_п2 есть функция вертикального перемещения подрессоренной массы Z , угла поворота подрессоренной массы 5 и вертикальных перемещений непод-рессоренных масс ^ ^₂. Выполним следующие преобразования:

d( П п 1 + П п ₂ ) _ -Г ^{п 1}С пi (f,M-Q.qiVjdf n 1 . d ]/ ^{п 2} С п2 n 2 ₂ ))df, 2 _ d ]/ ^{п 1} С п 1 (f i (Z,S,4 i ))df _n 1 df 1 + dZ ""           dZ                         dZ                        df ₁            ' dZ

. d$ Q^{п 2}С п2 (f п2 (Z,d,q2)')df п 2 df 2

ния, получим d( П п 1 + П п 2 )

dZ

локального анализа, т. е. возможность распространения результатов анализа единственной (непосредственно «просчитанной») точки пространства (5) на все пространство (5).

Таким образом, для решения вопроса о возможности «нелокального использования результатов локального анализа динамических систем» достаточно привести уравнения движения исследуемой динамической системы к нормальному виду и далее убедиться в том, что в расширенном пространстве конструктивных параметров исследуемой динамической системы правые части упомянутой выше нормальной формы удовлетворяют условиям Липшица.

Выводы

В статье рассмотрен вопрос о правомерности нелокального использования результатов локального анализа при численном решении систем дифференциальных уравнений, описывающих движение динамических систем. Показано, что для обобщения решения, полученного в одной точке пространства параметров, на все определенное пространство необходимо, чтобы правые части системы, приведенной к нормальной форме, удовлетворяли условиям Липшица.

Обсуждение и применение

Актуальность проведенного в статье исследования не вызывает сомнений, так как проблема использования результатов «локального» эксперимента в нелокальной области параметров часто возникает при анализе динамических систем различной природы и назначения. Более конкретно полученные в статье результаты могут быть широко использованы при проектировании узлов автомобилей, например, при проектировании адаптивных подвесок с нелинейными упругими элементами и управляемыми амортизаторами с гипершироким семейством характеристик [5]. При этом возможно разработать адаптивные подвески, обеспечивающие высокий уровень комфорта водителя и пассажиров, высокий уровень плавности движения автомобиля, резкое снижение в конструкции динамических нагрузок на узлы и детали автомобиля, перевозимый груз, членов экипажа и пассажиров. Вместе с тем, разработанные подвески будут отличаться безопасностью движения транспортных средств, хорошей управляемостью и защитой от перегрузок в экстремальных условиях вождения. Все эти свойства очень важны с учетом далеко не идеальной дорожной сети России. Заметим, что доказательство возможности использования результатов «локального» эксперимента на нелокальную область параметров имеет универсальный характер и позволяет избежать многих ошибок при попытках обобщения результатов анализа конкретных конструкций динамических систем на все конструкции этих систем в области расширенного множества семейства этих конструкций [18–20].

Статья выполнена при поддержке Правительства РФ (Постановление № 211 от 16.03.2013 г.), соглашение № 02.A03.21.0011.