О нелокальных краевых задачах для квазилинейного уравнения с вырождением порядка и типа

Рассмотрены вопросы существования и единственности решения квазилинейного уравнения с вырождением порядка и типа.

В работах А. В. Бицадзе [1, 2] отмечено, что для уравнения y2m^. + у2-1^ + аД, ди. + ЬД, ди, + ф, ДП = О,

где m и п натуральные числа, с вырождением типа и порядка классические краевые задачи не являются корректно поставленными. Там же для модельного уравнения у2™^ + yUyy + XU, = О, А = const.

указана методика постановки аналогов классических краевых задач.

Представляет интерес исследование нелокальных краевых задач для более общих уравнений, сохраняющих основные свойства этого уравнения и установление структурных свойств решений. На этом пути встречаются принципиальные трудности (см. [2]).

Рассмотрим квазилинейное уравнение

y^2mU_xx + yU„ + XUy + y^2mU² + yU² — О

в области D, ограниченной нормальным контуром ст:

( —-—) y2m+1 = О V2m + i;

при у > О

и характеристиками

АС : х-

2     , х 2т±1_

-------~У 2

2m У 1

ВС : х +

2771 + 1

(-у)

2т+1

2   = 1

уравнения (1) при у < 0.

Пусть Р+ kp-^ — эллиптическая (гиперболическая) части области D, т г           ,    „ , х х / 2m + 1 А 2™+1

I = {0 <  х < 1}, 0_о(ж) = --г(----- х\

_ , .    1-Х    / 2771 + 1        \ 2т + 1

точки пересечения характеристик уравнения (1), выходящих из точки ж G I с характеристиками АС и ВС соответственно.

Задача 1. Найти функцию U^ = U^x,^ со следующими свойствами: U^ G C^D^U C\D⁺ П D^-Y U^ — регулярное в D⁺ П D^- решение уравнения (1), удовлетворяющее условиям

П(ж,у) = <^(ж,у),   (ж,у) Ger,(2)

а(ж) ехр И(0о(ж)) + /Дж) ехр И(02(ж)) = 7(ж)

ИЛИ

—- ехр П(0о(ж)) + Ь— ехр [ДОДж)) = у(ж), ажаж lim yXUy ехр U(x, у) = lim (— y)XUy ехр(ж, у) = «(ж).(4)

улОДул-0-

Предположим, что функция «(ж) G С²)/) и при ж = 0, ж = 1 может обращаться в бесконечность порядка меньше 1 — 2е, где е = ^Д¹^²'’¹ ’

а(ж) = хра*(Х), р > 2s, а*(ж), /Дж), 7(ж) G С'3(7),(5)

(а*(ж)жр-Д1 — ж)е —/Дж) cos тге)2 +/12(ж) sinvrE Д О (Уж G 7).(5')

Единственность решения задачи 1 вытекает из принципа экстремума [2], который формулируется так: решение U^x,y) задачи 1, когда 7 = 0, положительный максимум и отрицательный минимум в замкнутой области D принимает на дуге о.

Для доказательства существования решения задачи 1 трансформируем уравнение (1) по формуле U = Ф(Е), где Ф(и) и У(ж,у) пока произвольные функции.

+ ’"1 + + уУ_уу + АУДФу + <у^ + уУ^_от + Ф²) = 0.

Отсюда видно, что уравнение (1) будет удовлетворено, если разрешимы нелинейное обыкновенное дифференциальное уравнение

Фет + Фу = 0, Фу(У) Д 0(6)

и уравнение

?mV«« + уУуу + ХУу = 0.(7)

Нетрудно видеть, что решением уравнения (6) является функция Ф = In V(х, у), а для определения У(х, у) имеем линейное уравнение (7). При переходе от функции И(ж,у) к У(ж,у) условия (2)-(4) переходят в условия

У(ж,у) = е*’= у?(ж,у), (ж,у)бсг,(2')

а(ж)У(0о(ж)) + /?(ж)У(01(ж)) = 7(ж),(8)

-^-Е(0о(ж))+ 6-^(0^)) =7(ж),(8')

ажаж lim улУ„(ж,у) = lim (—у)лУ„(ж,у) = «(ж).

ую0+             ул-0-

Рассмотрим сначала случай, когда m = 1, А = 0. Тогда уравнение (7) переходит в уравнение Трикоми относительно V

IjVxx + Гуу — 0,

(Ю)

а краевые условия принимают вид

ГДж, у) = Дж,у),   (ж,у) Е ст, lim (ж, у) = у(ж).                   (9')

у^0+

Регулярное в области 1) решение задачи выписывается в виде [2]

ГДж,у)=-/ v(t)G(t,0'x,y) dt -    ^(s)p(s-,x,y)ds.

Jo                      Jo

Здесь Дз;ж,у) есть решение некоторого интегрального уравнения, С(Ду;ж,у) — функция Грина.

В случае нормального контура ст функция Грина С(Ду;ж,у) выписывается в явном виде. Полагая в этой формуле у = 0, с учетом свойств функции Грина и гипергеометрической функции, имеем

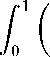
ж — t\ з

^^^^^^^™

(ж + 1-2ж1)1

)yW

dt = Дж),

где к = const, ф^ — аналитическая относительно ж функция, зависящая от Дж, у). Это есть основное соотношение между т(ж) и Дж) принесенное из D⁺.

Формула Дарбу, дающая решение задачи Коши для уравнения (10) с начальными данными

V(x, 0) = т(ж), lim ГДж, у) = Дж)

у^0- имеет вид

ИД = ГДж,у) = ух / т^ж + |(-у)2(21 - 1)^) (Д1 - Д) в dt

+ (Д 72У^ у(у + |(-у)Г21 - ШМ1 - t))~^ dt, где 71 = Г(1/3)/Г2(1/6), 72 = (3/2)2/3Г(5/3)/Г2 (5/6).

Подставляя в (11) z = ©о(ж) и z = 0Дж) будем иметь

• 2 Гж                    е            Г^1

ГД0о(ж)) = 71ЖЗ r(t)(t(x — Д)-ё dt — 72 v(t)(t(x — t))~s dt, JoJo

• У(01 (ж)) = 71(1 — ж) з [ r(t)((t — ж)(1 — ДДё dt — 72 [ ж(Д((1 — ж)(1 — I))^-e dt.

J XJ X

Удовлетворяя краевое условие (8), получим т^ dt (Дж - 1))1 „ fl

^^^^^^^™

Г u^dt А Jo (Дж — Д) ё / т(Д dt

((1 - ж)(1 - 1))б

^^^^^^^™

¹       ж(1) dt

⁰ ((1 -ж)(1 - 1^6

) = 7(ж).

Равенство (12) еств основное соотношение между т(ж) и «(ж), принесенное из области D^- на линию вырождения типа и порядка.

Исключая т(ж) из соотношений, связывающих т(ж) и «(ж), принесенных из эллиптической и гиперболической частей области D на линию у = О, после некоторых тождественных преобразований получим интегральное уравнение

и(ж) + /K(x,t)v(t) dt = 7(ж), Jo где К^х,^ и 7(ж) известные функции, обладающие свойствами обеспечивающими фред-гольмовость этого уравнения исходя из условий (5) и (5'), наложенных на заданные функции.

Найдя и(ж) и восстанавливая по ней У(ж,у), находим решение И(ж,у) нелинейной задачи 1.

Рассмотрим случай, когда А = | — т. Регулярное в области Р⁺ решение У (ж, у) уравнения (7), удовлетворяющее условиям

У(ж,0) = т(ж), У (ж, у) = <р(ж,у),   (ж,у) Е ст, lira уЛУу = «(ж).

имеет вид [2]

т(ж) = — (In \t — ж — \t + ж — 21ж|)и(1) dt.                    (13)

Jo

Регулярное в D- решение уравнения (7), удовлетворяющее условиям У(ж,0) = т(ж), lim (—у)АУу = и(ж), выписывается в виде х х 1         2   , .мА . 1     .    2   , .мА

^ ^ = У ж,у = -т ж--—— -у ²  +-т ж + -—— -у ²

2 V     2 771 + 1           /    2 V 2 777 + 17

2   .         Г1 /    2(1-21).   .2т±1А

-д—^{-у 2 у ж}++1— l^dt-

2т + 1          Jo \     2?7z + 1/

Подставляя в (14) z = 0о(ж) и z = 01(ж) получим

У(0_о(ж)) = ^т(О) + т(ж) - ^ x^dt^, У(01(ж)) = ^^т(1) + ^Т^ “ j v^ dt^ .

Удовлетворяя краевое условие (8), после некоторых преобразований будет иметь рХpl

а(ж) / v(t) dt + /3(ж) / v(t) dt = 71(ж), JO                 J х

где

71(ж) = т(0)а(ж) + т(1)^(ж) + т(ж)(а(ж) + /3(ж)) - 2д(ж).

Исключая т(ж) из (13) и (15) получим интегральное уравнение эквивалентное задаче (7)-(9). Учитывая, что без ограничения общности можно считать, что <р(ж,у) = 0, а следовательно т(0) = т(1) = 0, имеем рх               pl

а(ж) / v(t) dt + /3(х) / v(t) dt =

JO                Jx

а(ж) + /?(ж)

7Г

f (In \ t — ж| — In \ t + ж — 21ж|)«(1) dt — 2y(ж), о

Исследование этого уравнения проводится по схеме предложенной в [4, 5]. По найденному и(ж) находим У(ж,у), а затем решение основной задачи (1)-(4).

Когда 1—^ < А < 1, решение У(ж,у) уравнения (7), удовлетворяющее условиям У (ж, у) = <р(ж,у), (ж, у) Е ст, lim уЛ = «(ж) в области Г) выписывается в квадратурах у^0+ по формуле [2]

У(ж,у)= /\(£)G(^M+                            ^Ест' (16)

У о                У о     V ^Э^ dr//

G^hM^k'"^ g^HH^klW- ^Ц Y

1 / 4 V2' Г2(/3)         2771 - 1 + 2А

4тг \ттг + 2/ Г2(2/3) ’ * - 2(2777 + 1)

2г

777 + 2

•2

< = £ +

27 - т + 2

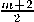
F — гипергеометрическая функция, сто ^— нормальный контур. При у щ 0 из (16) получаем основное соотношение между т(ж) и и (ж), принесенное на линию вырождения из

Регулярное в области D^- решение уравнения (7), удовлетворяющее условиям

У(ж,0) = т(ж), lim (—у)Л V^ (ж, у) = и(ж),   0 < ж < 1, существует, единственно и выписывается в виде [1]

У (г) = У (ж, у) = f т(х+ 2^ ^ (~у) ^) (1(1 - 1))е 1 dt 1 Уо \          + 1/

2   Г(1 — 2е) ,i_a Г1 /    2(1 -21), .тт+гА,

---л;-----г(^—у)        и(жН--(—у) 2 1(1(1 —1)) dt.

^т + ХГ^Д-еД Уо V 2m+ 1 k"

Из последнего равенства, при z = 0о(ж) и z = 01(ж), после некоторых преобразований, аналогичных [4, 5] и подстановки в (8) имеем

Г v(t) , _т , Г¹ и(ж) ,     /2т + 1А Г²(1-е)Г(2е)

тх -----—У1 + /5(ж)    —----—---- — dt = 2 ( ------ ]—------ —777 't-

Уо ^t^-t^^£ Jx ((1 - t^t - ж))^£      \ 4 у Г(1 - 2е)Г²(е)

( /*Ж        / \                                            с 1               ( \                \

а(ж)ж^{1-2е Т Ж} У1 + /?(ж)(1 - ж)^1-2е   — ------—-—dt\   (17)

Уо Wx-W ^{М М} ’ J_$ ((1-1)(1-ж))1"^£ j ^{k ;}

У 2777 + 1 ^ ^2е Г(1 — е)

у 4 У Г(1 - 2е) ^{П ;}

Это основное соотношение между т(ж) и «(ж), принесенное из области D^- на линию изменения типа и порядка у = 0.

Исключая т(ж) из системы (16), (17), связывающей т(ж) и «(ж), получим обобщенное уравнение Абеля относительно «(ж)

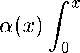
(1(ж - 1))£

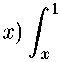
((1 - t^t - ж))^£

dt = Х(ж),

Р(ж) = I* ki^x,t)u^t) dt + f k2(x,t)v(t) dt + су(х), Jo                  Jo где кл\хЛ\ = c-\a\x\x —----—-—at,

Jo W-W-E

эквивалентное задаче (7)-(9).

Уравнение (18) по схеме предложенной в работах [4, 5] сводится к сингулярному интегральному уравнению, для которого указываются достаточные условия разрешимости. Имея и(ж), решая соответствующие задачи, находим У(ж,у), а затем решение И(ж,у) исходной задачи.

Случай краевых условий (3'), (8') рассматривается аналогично. Заметим, что когда А не принадлежит полусегменту (| — т, 1), исходную задачу можно рассмотретв используя результаты, полученные в [6].