О необходимости функционирования инфраструктуры поддержки малого инновационного предпринимательства

В настоящее время известно множество химических реакций, инициируемых лазерными импульсами. Под воздействием мощных лазерных импульсов во многих средах происходит нарушение равновесного состояния, которое сопровождается химическими реакциями (см.: [3; 6–11]). Это явление впервые было открыто и исследовано в работах Дж. Портера, М. Эйгена и Р. Норриша в 50–60-е гг. XX века. Временное разрешение при измерении длительности импульсов составляло 10-3 с. Несколько позднее для инициирования химических реакций стали применять короткие лазерные импульсы (см.: [9; 11]). Позднее мощность импульсов росла и их длительность сокращалась; появилось новое направление, называемое фемтохимией [11]. В настоящее время известно множество химических реакций, протекающих под воздействием электромагнитного излучения (см.: [3; 6–11]). С помощью фемтосекундных импульсов исследуются процессы фотосинтеза [10], фотодиссоциации гемоглобина [6], кинетики зрения [3]. По изменению формы лазерных импульсов можно судить о наличии химической реакции в биологических средах [3]. Известны сотни реакций горения и взрыва в неорганических газовых смесях, которые вызываются лазерными импульсами длительностью 10-5 с [8]. При помощи импульсов электромагнитного поля молекулы возбуждаются до энергии активации данной химической реакции, поэтому можно управлять реакцией, «указывая» ей необходимое направление. Поскольку концентрации химических веществ в составе среды зависят от времени, это должно отразиться как на ее линейных оптических свойствах, так и на нелинейных. Изучение влияния скорости реакции на диэлектрическую проницаемость и нелинейную восприимчивость среды, а также пре- образование формы огибающей оптического импульса как результат взаимодействия с реагирующей средой составляют цель настоящей работы.

В работах [4; 5] была найдена математическая модель оптических свойств реагирующей среды, взаимодействующей с электромагнитными импульсами. Выражения для диэлектрической проницаемости и нелинейной восприимчивости получены путем решения кинетического уравнения методом последовательных приближений по полю [2]. Вектор электрической индукции D определяется свойствами среды:

D = E + 4п P ,              (1)

где P = х E .

Если напряженность электрического поля падающей на среду электромагнитной волны сравнима с напряженностями полей, действующих между частицами среды, то эта связь уже не будет описывать происходящих в среде явлений. В этом случае поляризацию среды можно представить в виде *            *                *

P = pL + pNL.(2)

P^NL – нелинейная часть поляризации, ее можно представить в виде

PNL = p(2) + p(3) +...,(3)

где каждое из слагаемых в нелинейной части пропорционально указанной в скобках степени напряженности поля E :

P (2}= X^EpEk.(4)

Пусть в среде имеется n типов носителей зарядов – положительных и отрица- тельных ионов и электронов. Многокомпонентная среда при отсутствии электромагнитного излучения находится в равновесном состоянии и химических реакций в ней не происходит. Тогда для каждого типа зарядов i массой mi в любой момент времени t справедливо распределение Максвелла:

/       Л /2 - m i V

f ( t , r,v ) = f o ( r,v ) = N l /\ I e 2^   (5)

( 2П К Т )

где v - скорость частиц;

r - радиус-вектор;

N – концентрация зарядов -го сорта в точке ^r , причем

+и

J f ( , r, v ) dv = N .              (6)

—to

При взаимодействии со средой сверхкороткого оптического импульса заряженные частицы среды будут двигаться в переменном электромагнитном поле, равновесие в среде нарушится, изменятся функции распределения частиц по скоростям. Это изменение можно записать в виде: f (t,r,v) = f 0 + f, + f2. Первое слагаемое вычисляется по формуле (5), второе – изменением функции распределения скоростей зарядов под действием переменного электрического поля, а третье определяется движением частиц в переменном магнитном поле. Кроме того, в среде происходит химическая реакция. Число частиц каждого сорта будет меняться, но при этом должен выполняться закон сохранения электрического заряда ^Niqi = const и закон сохранения количества вещества ^Nimi = const. Первое приближение f .1 по полю в случае двухкомпонентной среды было найдено решением системы кинетических уравнений для реагирующей среды [1]. Неравновесные части f 1 функций распределения частиц по скоростям были применены для нахождения вычисления тока смещения, а затем диэлектрической проницаемости среды:

i — N j ( q + L 22 ^m

£ ( © ) = 1 + Л 7----------------

N2 T N. т Л .q2\

— Lj2 +--L j I + z — N2 (to +1L j) m 2 mj )

2 • to ( to — Q j )( q — q₂ )

В последней формуле введены обозна-λ1

чения: ®i = —, ш2 = —, A12 - собственные , значения матрицы кинетических коэффициентов реакции [4; 5].

Формула (7) справедлива как для одиночного импульса, так и для периодических импульсов, при этом форма огибающей может быть произвольной [5].

Пусть плоская электромагнитная волна частоты о с огибающей, произвольным образом зависящей от времени, с линейной поляризацией с азимутом 45° падает на многокомпонентную среду под углом 0 _z (рис. 1). В среде под воздействием излучения происходит химическая реакция.

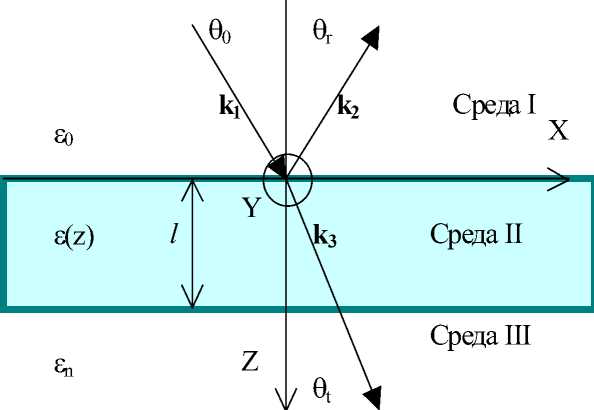
Рис. 1. Распространение света в плоской неоднородной среде толщины d ( k₁, k₂, k₃ – волновые векторы падающей, отраженной и прошедшей волн соответственно)

Найдем решение уравнений Максвелла для такой среды. Возникающие под действием электромагнитной волны коллективные процессы в среде учтем, подставив в уравнения Максвелла формулу (17) в работе [5] для тока смещения. Будем учитывать, что исходя из закона Снеллиуса — A ■ ik। • A ■ ia—• A, а из dx               c d ,      , , „ симметрии задачи следует, что —A ■ ik A ■ 0. dy

Из уравнений для роторов получим систему дифференциальных уравнений для проекций полей E и H в частных производных:

( e, ( — ) I    (           0

d dz

H - ( — )

h , ( — )

—

■ ic

I E - ( — ) J    I

- - Z q i q j N j K , !—) 2ω i , m

I-(

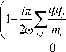
α

1 - in Z q i q j NK ^—) - a²

2ω i , m

| E y ( — ) I

⁰           I

⁰             H x ( — )

■ H y ( — )

^[ E x (—L

Введем обозначение

- 1

dEy  1 dH yx dz    c d t ’

^H ■ ikH

|| z

+ cE + ' jZ ;   ( t - T E №T,

<

^d H y = d z

¹ I ^Et" ^{+ П}I Z qq Nh ^{( t - T} ) E y ^{( t ) d T} I , c ( 5 t 2 0j m ,                J (8)

d e    1 a H y

—- ■---- + ikE ,

5 z       c a t       ¹¹ z ’

1 d H. c 6 t

= ^- ik l ^E y ,

—| —- + — [V — -N.h..(t - t ) E ( T ) d t I = ikH .

I                                                                  j i                                                 I 1 y c V d'    2o i,j mj                       )

= ( — ) ■ 1- in- Z q^q j N . K , ( — ) .

2ω i , m

Тогда система (11) примет вид, аналогичный описывающей распространение плоской электромагнитной волны в плоской однородной изотропной среде [1]. Система кинетических уравнений [2] реагирующей среды была решена во втором приближении по полю [4; 5]; получено выражение для тензора третьего ранга нелинейной восприимчивости многокомпонентной среды:

X^^{) (} — ) ■ ^ X

Здесь h_i ( t ) – импульсная реакция системы кинетических уравнений реагирующей среды. Выполним преобразование Фурье над системой (8). При интегрировании производные по времени дают множитель i м , останется только дифференцирование по переменной z :

^dEy ^(—) i —   / X

—j= —H-(—), dz c dH^ ■ ik |Hz (—)+ i— Ey, (—)+A Z qiqjNyK^—)Ey, (—), dz                  c          2c i, m dHy(—)    i— „ / x П gig,, x

—,  = Ey (—)-^-Z jNKj(—)Ex (—), dz c          2c i, j mj                             (9)

dE, (—) i — „ / x ,      ( x

—^==-—H1,(—)+ik lEz(—), i— Hz(—)=- ikEy(—), i— Ez (—) + ;П Z qiqjN^t (—) Ez (—) = ik|Hy (—).

c            2 c i , j m_j

Обозначим:

a ² =| k l I = e sin ² ( 9, ) .            (10)

I k 0 1

Исключим из уравнений (9) проекции H_Z и E_Z , получим систему из четырех обыкновенных дифференциальных уравнений:

X

Nq- ( — + iL 22 )( — + i ( L 22 - L 21 )) - N 2 ^{q 2} ( — + i"L 1X — + i ( L 11 - L 12 )) + m 1                         m 2

+ q i q ^⁽⁽ gN 2 + g , ^{N )} L 2 L 21 + i ( gN 2 L _c ^(— + // ,2 ) + g 2 N , L ,1 ^{( —} + /L 1 )))

I mm>                                             J

x a , i,k

Здесь a , _k - тензор третьего ранга, символ А ² обозначает

А ² ■ ( — - —₁ )( — - —₂ )( 2— - —₁ )( 2— - —₂ ) . (13)

Решение задачи о распространении света в реагирующей среде для линейного случая сводится к уравнениям (9) и (11) и расчету коэффициента отражения. Отраженное поле первой гармоники имеет в спектральном представлении вид

E R ( — ) ■ R ( — ) E ? I ( — ).             (14)

Во временном представлении связь (14) имеет вид

t

E R ^{( t} ) = j ^{R (} t ^{- t ) e} i ^{( t ) d T} .           (15)

Формула (13), также как и (7), была получена методом импульсной реакции и с по- мощью преобразований Фурье. Формула (7) позволяет рассчитать изменение формы оптического импульса, имеющего несущую частоту, близкую к действительной части одной из собственных частот го12 системы кинетических уравнений, при отражении его от реагирующей среды. Огибающая импульса – аб- солютно интегрируемая функция времени произвольной формы.

Рассмотрим гауссов радиоимпульс (см. рис. 2, 3). Зависимость вектора электрического поля от времени имеет вид

E i ( r ,t ) = E 0 exp{ikr - e ( t - t ) ² ) cos ( m _ct ) . (16)

E rs (t), E rp (t), отн. ед.

0.3

Ep Es

0.2

0.1

0.0

-4

-2      0      2      4      6       8      10     12     14

-0.1

10 ^-13

c

-0.2

V

-0.3

Рис. 2. Отраженный одиночный гауссов радиоимпульс при го _с = го 1

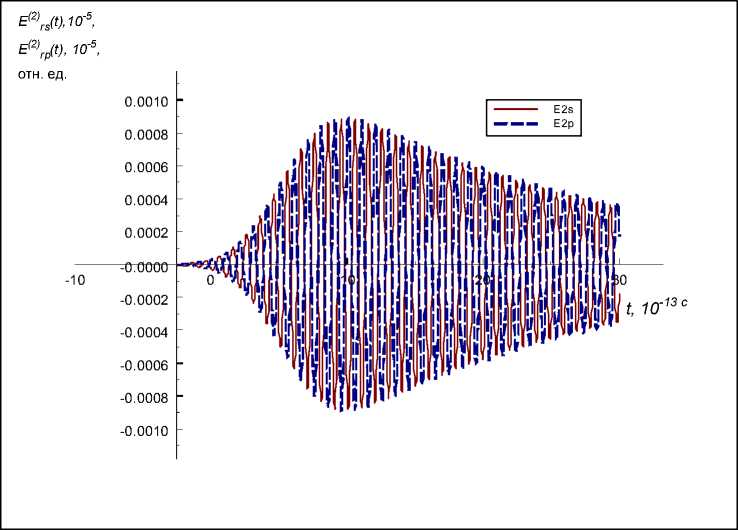
Рис. 3. Отраженный одиночный гауссов радиоимпульс второй гармоники при го _с = го 1

Рассмотрим прямоугольный радиоимпульс той же частоты и длительности т c (рис. 4,5). Зависимость сигнала от времени имеет вид

E i ^{( r}, ^to) = E 0 ^exp ( * ^? ) c°s ( to c t ) ^ t + 2- У ^ t — ^2 ^ .(17)

В случае пилообразного радиоимпульса зависимость вектора электрического поля от времени имеет вид

E ( r , t ) = Al ₀exp ( zk r ) at cos ( to _ct ) [ o ( t ) - o ( t - т ) ] . (18)

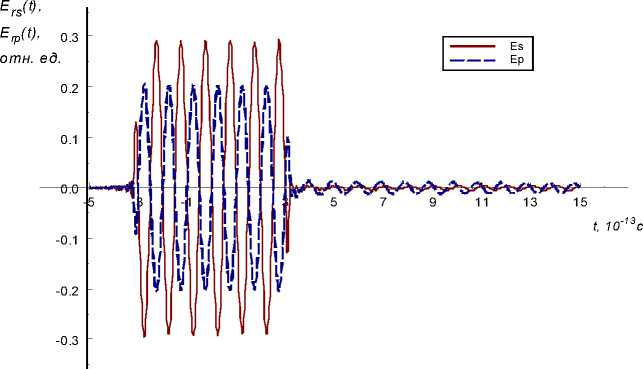
Рис. 4. Отраженный одиночный прямоугольный радиоимпульс при ю c = ю 1

A rs (t),

A rp (t),

0.001 5

E2s

E2p

10-5 отн. ед.

0.001 0

0.0005

-0.0005

-0.001 0

0.0000

-1 0.0

0.0

t, 10-13c

-0.001 5

Рис. 5. Отраженный одиночный прямоугольный импульс второй гармоники при частоте сигнала лазерного импульса ю _с = ю 1

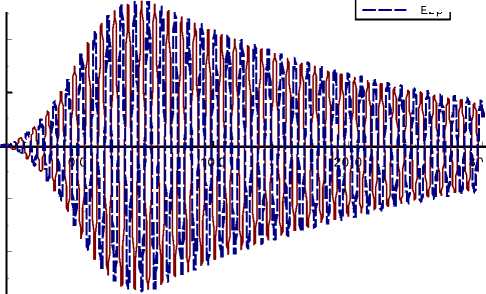
Зависимость от времени отраженных сигналов первой и второй гармоники для волн s - и p -поляризаций показаны на рисунке 6.

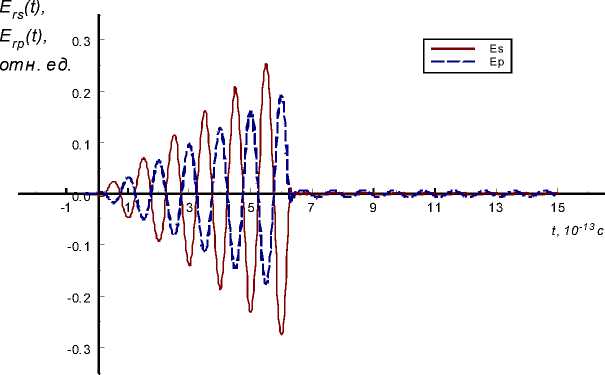
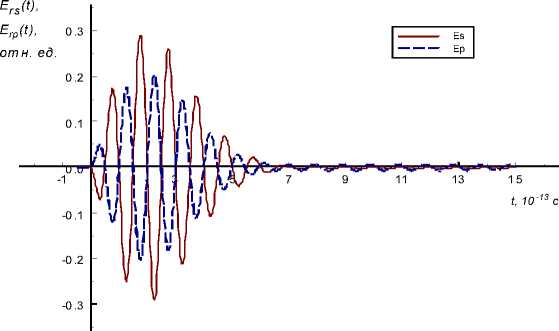
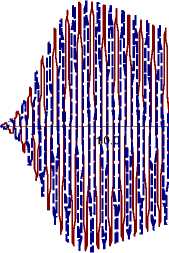
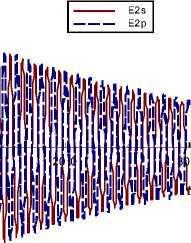
Рассчитаем форму отраженного гигантского радиоимпулься (рис. 7). Зависимость от времени вектора напряженности электрического поля имеет вид

E ( t ) = at exp( - e t 2 )sin(® _ct ) .        (19)

а

E⁽²⁾ rs (t),

E(2)rp(t), 10-5, отн. ед.

0.0 00 4

0.0 00 3

0.0 00 2

0.0 00 1

-0.0000

-0.0001

-0.0002

-0.0003

-0.0004

t, 10-13c

б

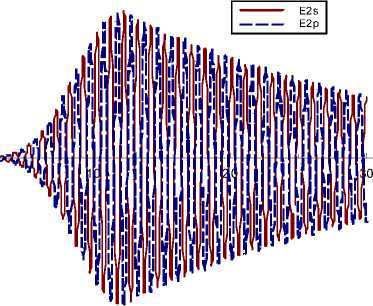
Рис. 6. Отраженный одиночный радиоимпульс пилообразной формы: а - первой гармоники при ю _с = ю 1 ; б - импульс второй гармоники при частоте сигнала лазерного импульса ю _с = ю .

а

E(2)rs(t),

E⁽²⁾ rp (t), 10^-5 отн. ед.

0.0 00 5

0.0 00 4

-10.0

0.0 00 3

0.0 00 2

0.0 00 1

0.0 00 0

0.0

-0.0001

-0.0002

-0.0003

-0.0004

, 10-13

-0.0005

б

Рис. 7. Отраженный одиночный гигантский радиоимпульс: а - первой гармоники при ю c = « 1 ; б - импульс второй гармоники при частоте сигнала лазерного импульса ю c = « 1

Для сигнала любой формы E ( t ), падающего на среду, отраженного или прошедшего, можно рассчитать его спектральную плотность. Тогда энергетический спектр отражения связан со спектрами падающей и отраженной волн формулой:

g^z \ Er (ю), Er (to)             (20)

^Л(ю)       W*   .         ^{( )}

Ei(®),Ei (ю)

Особенности спектра отражения несут информацию о скорости процессов, происходящих в нестационарной среде.

Индуцируемые лазером химические процессы приводят к изменению оптических свойств реагирующей среды. Диэлектрическая проницаемость среды и нелинейная восприимчивость должны иметь резонансы на частотах, определяемых системой кинетичес- ких уравнений химической реакции. При взаимодействии со средой импульсов специальной формы наибольшее искажение формы сигнала и возрастание амплитуды сигнала второй гармоники наблюдается на этих частотах.