О непараметрическом моделировании безынерционных систем с запаздыванием

Введение. Идентификация многомерных стохастических процессов является довольно актуальной проблемой для многих технологических производственных процессов дискретно-непрерывного характера. В многочисленных многомерных реальных процессах выходные переменные доступны измерению не только в различные моменты времени, но и через длительное время.

На практике это часто означает, что контроль некоторых компонент вектора выходных переменных значительно превышает постоянную времени объекта. Это приводит к тому, что динамические по своему характеру процессы вынуждены рассматриваться как безынерционные с запаздыванием.

Настоящая статья посвящена задачам идентификации процессов, выходные переменные которых стохастически зависимы заранее неизвестным образом. Такого рода процессы в дальнейшем и называются Т -процессами [1]. А задача идентификации в данном случае состоит в построении Т -моделей многомерных статистических объектов.

Следует обратить внимание на то, что термин «процессы» ниже рассматривается не как процессы вероятностной природы, например, изложенные в [2], такие как стационарные, гауссовские, марковские и др. Ниже речь пойдет о Т -процессах, реально протекающих или развивающихся во времени. В частности, это технологический процесс, производственный, экономический процесс, процесс выздоровления человека и многие другие.

Данные процессы впервые были упомянуты А. В. Медведевым [3].

Т -модели. Система уравнений, описывающая Т -процессы, в общем виде может быть представлена следующим образом [4]:

F j ( u ( t ) , x ( t ) ) = 0, j = 1, n , (1) где u ( t ) - вектор входных переменных; x ( t ) - вектор выходных переменных. Но на практике часто имеет место ситуация, когда на основании априорной информации система уравнений (1) может быть представлена в виде

Fj(u(t), x(t)) = 0, j = 1n, (2) где u(t), x(t) - составные векторы. Составной вектор – это вектор, составленный из некоторых ком- понент соответствующего вектора, в частности x (t) = (u2 (t),u5 (t), x2 (t), x7 (t)), либо другой набор.

При этом основной особенностью моделирования подобного процесса в условиях непараметрической неопределенности является тот факт, что вид функций (1) неизвестен. В этом случае система уравнений (1) может быть представлена в следующем виде:

F j ( u < j > ( t ) , x < j > ( t ) , x s , u s ) = 0, j = 1, n , (3) где x s , u s - временные векторы (набор данных, поступивший к s -му моменту времени), в частности, x_s = ( x 1 , ..., x_s ) = ( x_m x ^, ..., x s , ..., x 21 , x 22 , ..., x _{2 s} , …, x_{n 1}, x_{n 2}, …, x_ns ) , но и в этом случае F j ( ' ) , j = 1, n , продолжают оставаться неизвестными. В теории идентификации подобные задачи не только не рассматриваются, но и не ставятся. Чаще всего идут по пути выбора параметрической структуры (1), но, к сожалению, преодоление этого этапа затруднено из-за недостатка априорной информации [5; 6], и требуется длительное время для определения параметрической структуры, т. е. представления модели в виде

F j ( u < j > ( t ) , x < j > ( t ) , a ) = 0, j = 1, n , (4) где a - вектор параметров. Далее следует процедура оценки параметров по элементам обучающей выборки u_z , x i , i = 1, s , с последующим решением системы нелинейных взаимосвязанных соотношений (4). Успех построения модели в данном случае будет зависеть от качественной параметризации системы (4) [7; 8].

В дальнейшем рассмотрим задачу построения Т -моделей в условиях непараметрической неопределенности, т. е. в условиях, когда система (3) не известна с точностью до параметров [4; 9].

Вычислительный эксперимент. Для вычислительного эксперимента был взят простой многомерный объект с пятью входными переменными u (t) = (u1 (t), u2 (t), u3 (t), u4 (t), u5 (t)), принимающими случайные значения в интервале u (t)е[0;3], и четырьмя выходными переменными x(t) = (x1 (t), x2 (t),x3 (t), x4(t)), принимающими зна- чения в следующих интервалах: x1(t) €[-2; 15], x2(t)€[-0,8; 33], x3(t)е[-0,7; 28], x4(t)€[-12; 47]. Для данного объекта сформируем выборку входных и выходных переменных исходя из системы уравнений (уравнение выбрано произвольно, но для алгоритма идентификации они неизвестны):

x 1 ( t ) - 2 u ₂ ( t ) + u ₅ ( t ) - 0,3 x ₂ ( t ) = 0;

x 2 ( t ) - u 3 ( t ) - 0,3 u 3 ( t ) - 0,5 x ( t ) = 0;

^x 3 ( t ) ^- u 4 ( t ) ^- V u 5 ( t ) ^{- 0,2} x 4 ( t ) = 0; x ₄ ( t ) - u 2 + u ₃ ( t ) - 0,4 x ₃ ( t ) = 0.

Система уравнений (5) не является описанием реального процесса, она принята только в данном вычислительном эксперименте. Данная система вводится для того, чтобы провести вычислительный эксперимент и сравнить результаты оценок компонент вектора выхода, которые получатся с помощью Т -модели, с истинными значениями, известными из системы (5). Данная система приведена только для исследования. Если бы мы имели дело с реальной задачей, то обучающая и тестовая выборка были бы получены при многочисленных опытах, проводимых с изучаемым объектом [10].

Таким образом, решая систему (5) относительно x(t) = (x1 (t), x2 (t),x3 (t), x4(t)), получим обучающую выборку u, x, i = 1,5 . Далее необходимо решить систему (5). Для этого необходимо решить ее относительно x (t) при известных значениях u (t), при этом значения u (t) могут быть сформированы случайным образом из указанных выше интервалов:

F x 1 ( ^x 1 ( t ) , ^x 2 ( t ) , u 2 ( t ) , u 5 ( t ) ) = 0;

F x 2 ( ^x 1 ( t ) , ^x 2 ( t ) , u ( t ) , u 3 ( t ) ) = 0;

F x 3 ( x 3 ( t ) , x 4 ( t ) , u 4 ( t ) , u 5 ( t ) ) = 0; _ F x 4 ( x 3 ( t ) , x 4 ( t ) , u 2 ( t ) , u 3 ( t ) ) = 0.

Таким образом, при известных значениях u ( t ) = ( u 1 ( t ) , u ₂ ( t ) , u ₃ ( t ) , u ₄ ( t ) , u ₅ ( t ) ) необходимо дать оценку значений выходных переменных. Это является основным итогом решения задачи идентификации. Конечно, хотелось бы назвать систему уравнений (5) моделью исследуемого процесса, но это не так, по той простой причине, что функции F ( x ) неизвестны. Именно поэтому в качестве Т -модели выступает цепочка соответствующих непараметрических статистик.

Для начала вычисляются невязки для каждого компонента вектора выхода по следующей формуле [4]:

8j (i) = F (u, xj (i)) = xj(i)-

5         <  П >

I j i П Ф i = 1           k = 1

uk^kti

c

V     5uk    7

5 <  П >

1П Ф

i = 1 k = 1

^u k ^{- u} k ^[ i ^]

V c u  7

где j = 1, n, , < m > - размерность составного вектора uk, < m > < m , в дальнейшем это обозначение ис- пользуется и для других переменных. Колоколооб- разные функции

Ф

^u k ^{- u} k ^[ i ^]

v      ^5u k    7

и параметр размыто-

сти c_suk удовлетворяют некоторым условиям сходимости и обладают следующими свойствами:

Ф (■) < ^;

c ;¹ J Ф ( c ;¹ ( u ^{- u}i)^d^u = 1;

Q ( u )

lim 5 ^„ ^с - ^1ф ( c - ¹ ( u ^{- u} i ) ) = 8 ( ^{u - u} i ) ;

^lim 5 ^„ c 5 = 0, ^lim 5 ^„ ⁵c 5 =* ^[H]-

Также можно представить невязки в виде следующей системы:

• ⁸1    ( i ) = F x 1 ( x i ( t ) , x 2 ( t ) , u 2 ( t ) , u 5 ( t ) ) ;

• ⁸2    ( i ) = F x 2 ( ^x i ( t ) , ^x г ( t ) , ^u l ( t ) , ^u 3 ( t ) ) ;

• ⁸3    ( i ) = F x 3 ( ^x 3 ( t ) , ^x 4 ( t ) , ^u 4 ( t ) , ^u 5 ( t ) ) ;

• ⁸4    ( i ) = F x 4 ( ^x 3 ( t ) , ^x 4 ( t ) , ^u 2 ( t ) , ^u 3 ( t ) ) .

Соответственно, каждая невязка соответствует конкретному выходу объекта.

Для данного эксперимента будем менять параметр размытости c_s . Параметр размытости будет лежать в интервале c₅ € [0,3; 1,2]. Объем выборки зададим 5 = 1000. Для каждого выхода объекта x 1 ( t ) , x ₂ ( t ) , x ₃ ( t ) , x ₄ ( t ) приведем графики прогнозных значений.

Так как объем выборки большой и чтобы наглядно было видно, приведем на графике прогнозные значения выхода модели с частотой через каждые 50 точек выборки.

На рис. 1–4 точками обозначен объект, а крестиками обозначена модель объекта.

Приведенные рис. 1–4 показывают истинные значения выходных переменных и их прогнозные значения. Как видно, истинные значения и прогнозные значения компонент вектора выхода дают довольно точный результат. Это свидетельствует о высокой точности Т -модели.

Второй эксперимент проведем с помехой 10 %. При этом помеха будет накладываться на значения компоненты вектора выхода объекта. Для данного эксперимента, как и в первом случае, будем менять параметр размытости c _s и процент помехи. Объем выборки зададим 5 = 1000 . Для каждого выхода приведем графики x 1 ( t ) , x ₂ ( t ) , x ₃ ( t ) , x ₄ ( t ) .

На рис. 5–8 точками обозначен объект, а крестиками обозначена модель объекта.

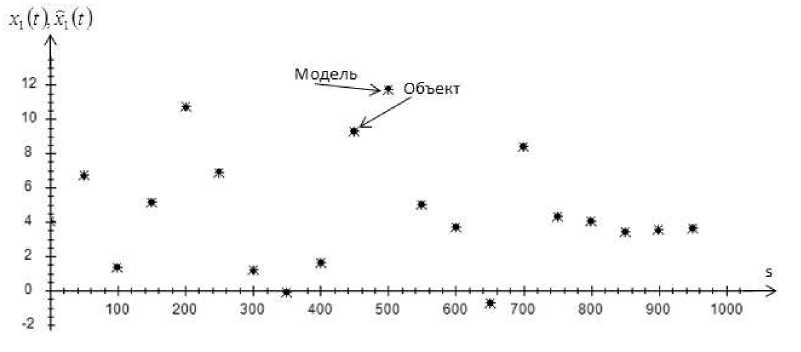
Рис. 1. Прогноз значений выходной переменной x ₁ без помех, при s = 1000 и c_s = 0,3

Fig. 1. Prediction of values of output variable x ₁ , without interference, at s = 1000 and c_s = 0,3

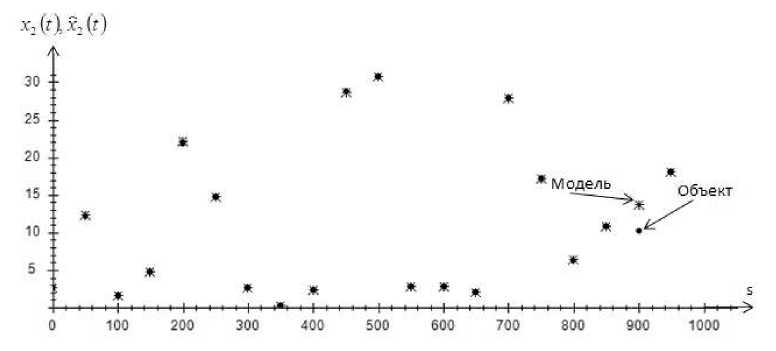
Рис. 2. Прогноз значений выходной переменной x ₂ без помех, при s = 1000 и c_s = 0,3

Fig. 2. Prediction of values of output variable x ₂ , without interference, at s = 1000 and c_s = 0,3

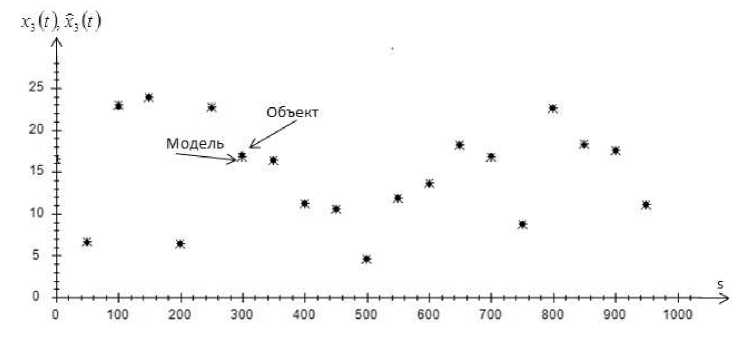
Рис. 3. Прогноз значений выходной переменной x ₃ без помех, при s = 1000 и c_s = 0,3

Fig. 3. Prediction of values of output variable x ₃ , without interference, at s = 1000

and c_s = 0,3

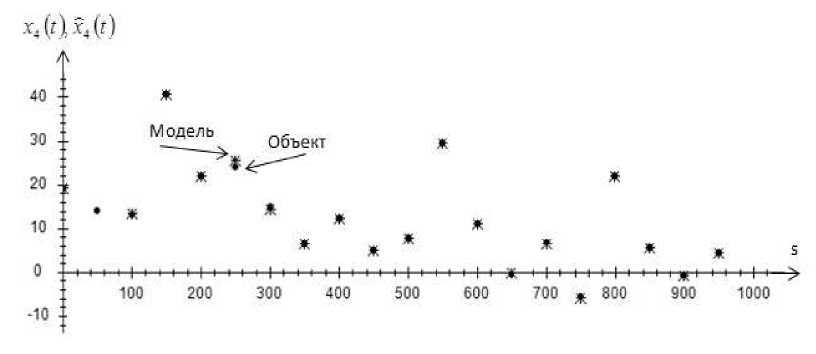
Рис. 4. Прогноз значений выходной переменной x4 без помех, при s = 1000

и c_s = 0,3

Fig. 4. Prediction of values of output variable x ₄ , without interference, at s = 1000 and c_s = 0,3

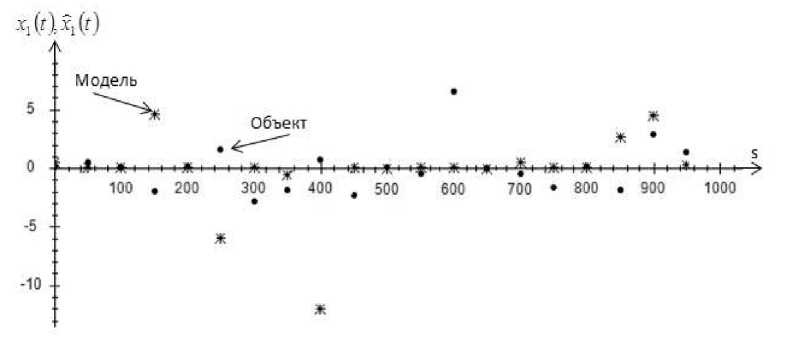
Рис. 5. Прогноз значений выходной переменной x ₁ при s = 1000 и c_s = 0,3 , помеха 10 %

Fig. 5. Prediction of values of output variable x ₁ , at s = 1000 and c_s = 0,3 , interference 10 %

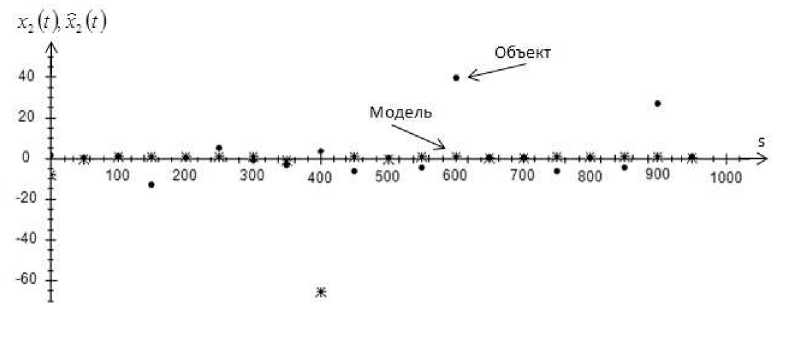
Рис. 6. Прогноз значений выходной переменной x ₂ при s = 1000 и c_s = 0,3 , помеха 10 %

Fig. 6. Prediction of values of output variable x ₂ , at s = 1000 and c_s = 0,3 , interference 10 %

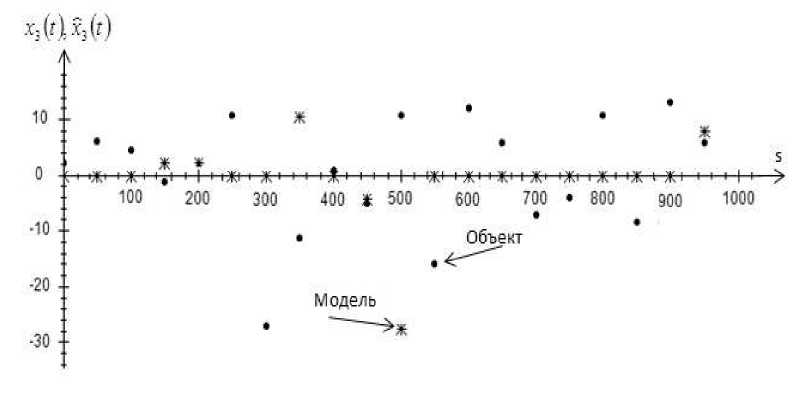
Рис. 7. Прогноз значений выходной переменной x 3 , при s = 1000 и c s = 0,3, помеха 10 %

Fig. 7. Prediction of values of output variable x ₃ , at s = 1000 and c s = 0,3, interference 10 %

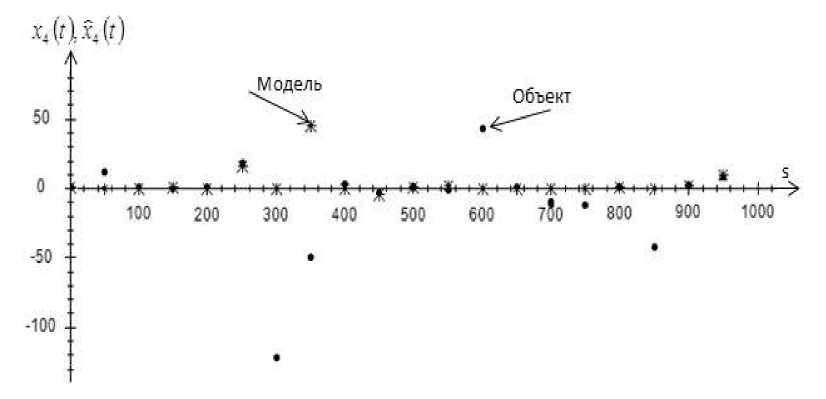
Рис. 8. Прогноз значений выходной переменной x 4 , при s = 1000 и c s = 0,3, помеха 10 %

Fig. 8. Prediction of values of output variable x 4 , at s = 1000 and c s = 0,3, interference 10 %

На рис. 5–8 показаны истинные значения выходных переменных и прогнозные значения выходных переменных. Как можно заметить из графиков, при помехе 10 % некоторые точки выборки отклоняются от истинных значений. Возможно, это происходит из-за того, что присутствует 10 %-я помеха и на вход могут поступать некорректные значения.

Также для сравнения увеличим объем выборки s = 2000. Как и в предыдущих экспериментах, будем менять параметр размытости c_s . Параметр размытости будет лежать в интервале c s е [0,3; 1,2].

Также для наглядности для каждого выхода приведем графики x 1 ( t ) , x ₂ ( t ) , x ₃ ( t ) , x 4 ( t ) . И то же проделаем с помехой 10 % для каждого из выходов.

На рис. 9–16 точками обозначен объект, а крестиками обозначена модель объекта.

Как можно заметить из приведенных графиков, с увеличением помехи до 10 % объект отклоняется от модели. А при увеличении объема выборки точность прогноза увеличивается.

Заключение. В данной работе была рассмотрена задача идентификации безынерционных многомерных объектов с запаздыванием при неизвестных стохастических связях компонент вектора выхода [12–14].

Проведенные вычислительные эксперименты показали высокую эффективность Т -моделиро-вания. Также при моделировании были произведены эксперименты с различным объемом выборки и помехами [15].

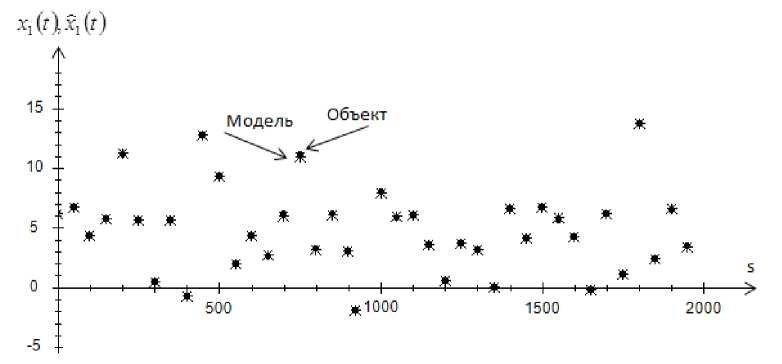
Рис. 9. Прогноз значений выходной переменной x ₁ без помех, при s = 2000 и c_s = 0,3

Fig. 9. Prediction of values of output variable x ₁ , without interference, at s = 2000 and c_s = 0,3

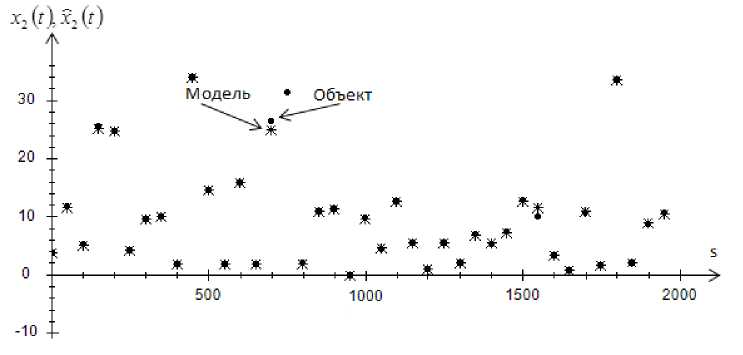
Рис. 10. Прогноз значений выходной переменной x ₂ без помех, при s = 2000 и c_s = 0,3

Fig. 10. Prediction of values of output variable x ₂ , without interference, at s = 2000 and c_s = 0,3

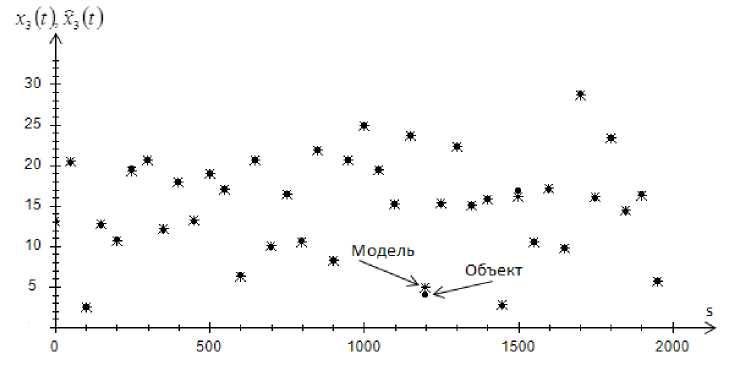
Рис. 11. Прогноз значений выходной переменной x ₃ без помех, при s = 2000 и c_s = 0,3

Fig. 11. Prediction of values of output variable x ₃ , without interference, at s = 2000 and c_s = 0,3

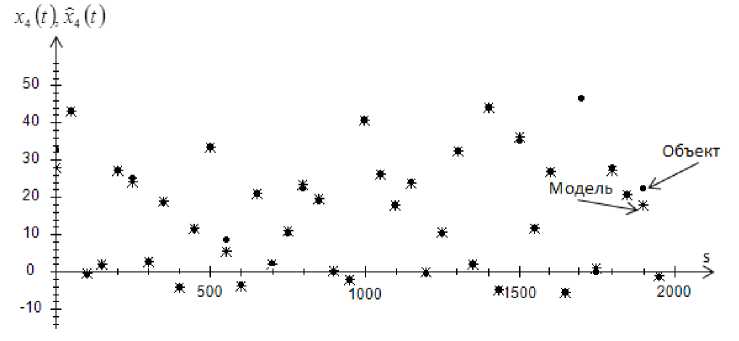
Рис. 12. Прогноз значений выходной переменной x ₄ без помех, при s = 2000 c_s = 0,3

Fig. 12. Prediction of values of output variable x ₄ , without interference, at c_s = 0,3

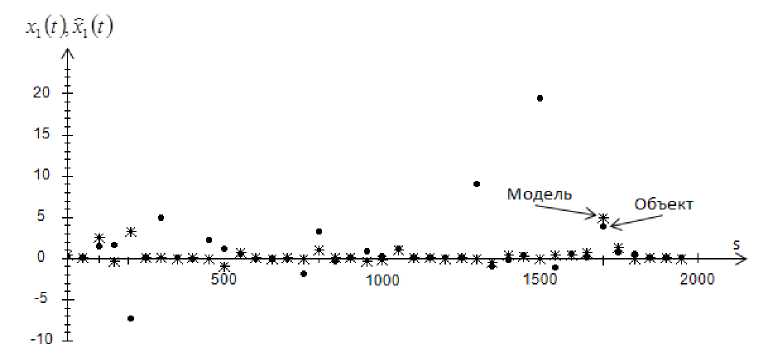
Рис. 13. Прогноз значений выходной переменной x ₁ при s = 2000 и c_s = 0,3 , помеха 10 %

Fig. 13. Prediction of values of output variable x ₁ , at s = 2000 and c_s = 0,3 , interference 10 %

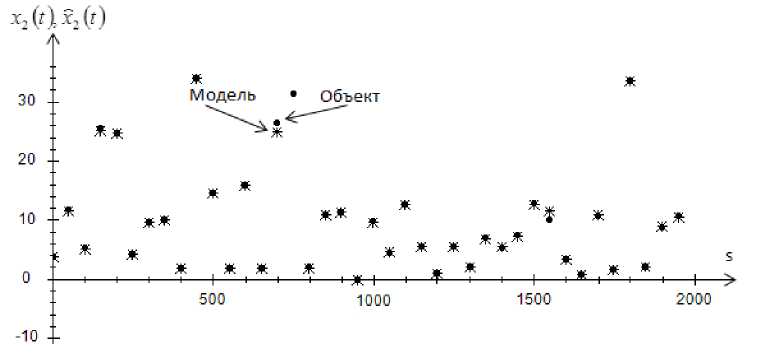
Рис. 14. Прогноз значений выходной переменной x ₂ при s = 2000 и c_s = 0,3 , помеха 10 %

Fig. 14. Prediction of values of output variable x ₂ , at s = 2000 and c_s = 0,3 , interference 10 %

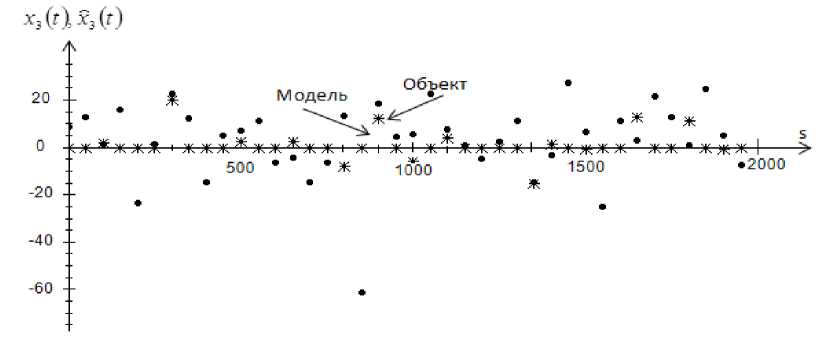
Рис. 15. Прогноз значений выходной переменной x ₃ при s = 2000 и c_s = 0,3 , помеха 10 %

Fig. 15. Prediction of values of output variable x ₃ , at s = 2000 and c_s = 0,3 , interference 10 %

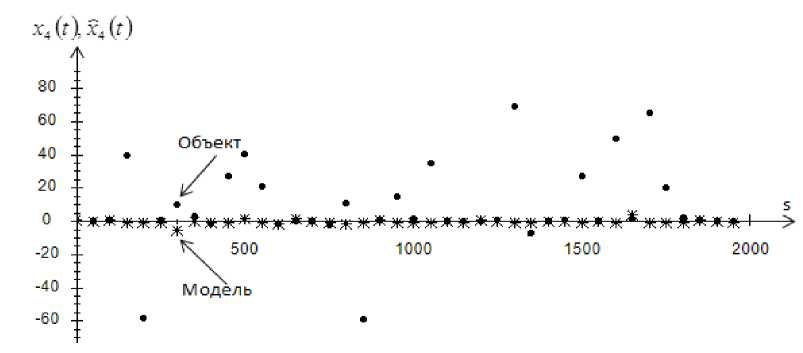
Рис.16. Прогноз значений выходной переменной x ₄ , при s = 2000 и c_s = 0,3 , помеха 10 %

Fig. 16. Prediction of values of output variable x ₄ , at s = 2000 and c_s = 0,3 , interference 10 %