О неприводимых коврах аддитивных подгрупп типа F4

Пусть Ф — приведенная неразложимая система корней ранга 1, Ф(К) — группа Ше-валле типа Ф над полем K. Группа Ф(К) порождается своими корневыми подгруппами xr (K) = {xr (t) : t E K}, r E Ф.

Подгруппы xr(K) абелевы и для каждого r E Ф и любых t,u E K справедливы соотношения xr (t) xr (u) = xr (t + u).

Мы следуем определениям В. М. Левчука из [2]. Назовем ковром типа Ф ранга 1 над K всякий набор аддитивных подгрупп A = { A r : r E Ф } кольца K с условием

C ij,rs A r A s С A ir+js ,  r,s,ir + js E Ф, i,j> 0,

^# Работа выполнена при финансовой поддержке Российского научного фонда, проект № 22-21-00733.

где А Г = { a i : a E A r } , а константы C ij, _rs = ± 1, ± 2, ± 3 определяются коммутаторной формулой Шевалле

[Xs (u),X r (t )] = Ц X ir + js (C ij,rs ( - t) i U^j) , r,s,ir + js E Ф. i,j> 0

Всякий ковер А типа Ф над K определяет ковровую подгруппу

Ф( A ) = ( x r ( A r ) : r E Ф )

группы Шевалле Ф(К) , где ( M ) — подгруппа, порожденная подмножеством M группы Ф(К) . Ковер А называется замкнутым, если его ковровая подгруппа Ф( А ) не имеет новых корневых элементов, т. е.

Ф( А ) П X r ( K )= X r ( A r ), r E Ф.

Назовем ковер A неприводимым , если все A _r ненулевые. Примеры незамкнутых неприводимых ковров типа A _l (матричных ковров) указаны в [3], а в [4] указаны примеры таких ковров любого лиева типа над коммутативными кольцами.

Основным результатом статьи является

Теорема. Пусть A = { A _r : r E Ф } — неприводимый ковер типа F 4 над полем K, все аддитивные подгруппы которого являются R-модулями, где K — алгебраическое расширения поля R. Тогда с точностью до сопряжения диагональным элементом либо A _r = P при всех r E Ф , для некоторого подполя P поля K, либо char K = 2 и

A = ^P, r _Q,

если r — короткий корень, если r — длинный корень, для двух различных подполей P и Q поля K , удовлетворяющих включениям

P ² С Q С P.

Кроме того, ковер A является замкнутым.

При p >  2 утверждение теоремы установлено в [1], и в этом случае ковер A параметризуется только одним полем.

• 2.    Предварительные результаты

Наряду с группой Ф(К) рассматривают расширенную группу Шевалле Ф(K) , которая является расширением группы Ф(К) при помощи всех диагональных элементов h(x) , где X — K -характер целочисленной решетки корней Z Ф , т. е. гомоморфизм аддитивной группы Z Ф в мультипликативную группу K * поля K [5, §7.1]. Любой K -характер х однозначно задается значениями на фундаментальных корнях и для любых r E Ф , t E K ,

^h(X^)x r (tNx) ¹ = x r ⁽X^(r)t).

Отметим, что в нашем случае, при Ф типа F 4 , группа Ф(К) совпадает с расширенной группой Шевалле Ф(К) .

Для доказательства основной теоремы нам необходимы следующие леммы.

Лемма 1 [6] . Сопрягая диагональным элементом h(x) ковровую подгруппу Ф( А ) , получим ковровую подгруппу

h(x)Ф(A)h(x)-1 = Ф(А‘), определяемую ковром

A ’ = { A ’ r : r Е Ф } , где A ’ r = x ( r ) A r .

Лемма 2 [5] . Любой положительный корень r Е Ф + может быть представлен в виде суммы фундаментальных корней r = p i + p 2 + ... + p k таким образом, что r = Р 2 + Р 2 + ... + P s является корнем для всех s ^ k.

Следующая лемма является частным случаем следствия 3.2 из [1] для системы корней типа A 2 .

Лемма 3. Пусть { a, b } — фундаментальная система системы корней Ф типа A 2 , A = { A r : r Е Ф} — неприводимый ковер над полем K, причем все A r являются R-модулями над полем R, где K — алгебраическое расширение поля R и 1 Е A _{- a} П A - b . Тогда A r = P, r Е Ф , для некоторого подполя P поля K.

Хорошо известна (см., например, [7])

Лемма 4. Пусть K — алгебраическое расширение поля R и подкольцо A поля K является R-модулем. Тогда A — поле, причем R С A С K.

Из теоремы 3.1 [8] вытекает следующий результат в случае Ф типа F 4 .

Лемма 5. Пусть K — алгебраическое расширение несовершенного поля R характеристики 2, и M — группа, лежащая между группами Шевелле Ф(R) и Ф(К) типа Ф = F4. Тогда M является ковровой подгруппой Ф(A). Ковер A = {Ar : r Е Ф} является замкнутым, и

A = ^P, r _Q,

если r — короткий корень, если r — длинный корень, для некоторых подполей P и Q поля K с условиями

R,P 2 С Q С P С K.

• 3.    Доказательство теоремы

Далее П = { r i ,r 2 , г з ,Г 4 } — фундаментальная система корней типа F 4 , причем r i , r 2 — короткие корни, г з , r 4 — длинные корни и сумма { r 2 + г з } также является корнем (см. рис. 1).

r 1            r 2            r 3             r 4

о--с^--о

Рис. 1.

Согласно определению фундаментальной системы корней, r = ar i + er 2 + Yr 3 + ^4 , где все a,e,Y,^ либо неотрицательные, либо неположительные, и r Е Ф ⁺ . По определению, h(r) = a + в + Y + ^ — высота корня. Все фундаментальные корни, очевидно, имеют высоту 1.

В системе корней типа F 4 имеются только две подсистемы корней ранга 2 — это подсистемы A 2 и B 2 (см. рис. 2, 3).

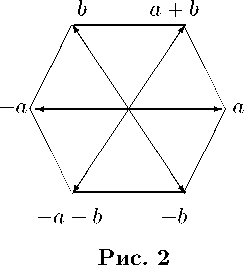
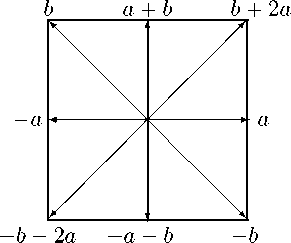
Рис. 3

Коммутаторная формула Шевалле для типа A 2 имеет вид

[x a (t),^x b (^u)] = x (a₊b) ( ± tu).

Данная формула дает условие ковровости

A a A b С A a + b .                                    (1)

Для типа B 2 справедливы коммутаторные формулы Шевалле

^[x a ^(t),x b ^(u)] = x (a+b) ⁽ ± t^u)x (2a+b) ⁽ ± t ² u ) ,

[Xa(t),Xa+b(u)] = X(2a+b) (±2tu), из которых получаем следующие три условия ковровости:

AaAb С Aa+b,

AaAb С A2a+b,

2AaAa+b С A2a+b.

По лемме 1 с точностью до сопряжения диагональным элементом, можно считать, что 1 G A r , r G П . Для любых двух неколлинеарных корней r,s через Ф(г, s) обозначим подсистему корней, порожденную этими корнями. В силу леммы 3 1 G A r для всех r G Ф(г 1 ,Г 2 ) U Ф(г з ,Г 4 ) (см. рис. 1). В частности, 1 G A r при h(r) = 1 . Индукцией по высоте корня h(r) покажем, что 1 G A _r для всех r G Ф ⁺ .

Согласно лемме 2, любой положительный корень r G Ф ⁺ может быть представлен в виде суммы фундаментальных корней r = p i + ... + p k + p k+i , где сумма p i + ... + P k является корнем. Обозначим ее через s , а фундаментальный корень p k+i через p . Высота r больше или равняется 2 . По предположению индукции 1 G A s П A _p .

Для системы корней типа F 4 становятся возможными только следующие три случая, когда сумма корней s и p является корнем:

• 1)    { s,p } — фундаментальная система типа A 2 ;

• 2)    { s,p } — фундаментальная система корней типа B 2 ;

• 3)    | s | = IpI = 1 , | s + p | = V 2 .

В случае 1), 2) из условий ковровости (1) и, соответственно, (2) получаем включение A s A p С A r , следовательно, 1 G A r .В случае 3) из условия ковровости (3) следует включение A 2 A p - s С A 2s+( _{p - s} ) = A r , следовательно 1 G A r . Аналогично индукцией по модулю высоты корня получаем, что 1 G A r , r G Ф ^- .

Итак, мы установили включения 1 G A r для всех r G Ф . Поскольку группа Вейля действует транзитивно на корнях одинаковой длины, а любой фундаментальный корень лежит в подсистеме корней типа A 2 , то в силу леммы 3 каждая аддитивная подгруппа A r является полем и, более того, A _{- r} = A r . Покажем, что A r = P для всех коротких корней и A r = Q для всех длинных корней, причем мы не исключаем совпадения полей P и Q .

По лемме 2 любой положительный корень r G Ф + представим в виде r = s + p , где p — простой корень и h(p) = 1 , h(s) = h(r) — 1 . Возможны три случая:

• 1)    { s,p } — фундаментальная система типа A 2 ;

• 2)    { s,p } — фундаментальная система типа B 2 ;

• 3)    s,p — короткие корни и они порождают подсистему корней типа B 2 .

В каждом из этих трех случаев по отдельности индукцией по высоте корней покажем, что A _r совпадает с P или Q в зависимости от длины корня r .

В случае 1) сразу получаем равенство A _r = A _p в силу индуктивного предположения и леммы 3, где A _p совпадает с P или Q .

В случае 2) корень p может быть как коротким, так и длинным. Пусть p — короткий корень. Тогда из условий ковровости A p A s С A r и A r A _{- s} С A p получаем включения P С A r и соответственно A r С P . Отсюда A r = P . Случай, когда p — длинный корень, рассматривается аналогично, нужно только поменять местами корни p и s .

В случае 3) разность s — p является корнем, p — короткий корень и { p, s — p } — фундаментальная система типа B 2 . Поэтому в силу индуктивного предположения A p = P , а A _{s - p} = Q . Сейчас из условий ковровости A p A _{s - p} С A r и A - p A r С A _{s - p} получаем включения Q С A _r и соответственно A _r С Q . Отсюда A _r = Q .

Таким образом, мы установили, что A совпадает с P или Q в зависимости от длины корня r . Если char = 2 , то ковер определяется одним полем и, следовательно, определяемые им ковровые подгруппы совпадают с группой Шевалле, и поэтому он является замкнутым. Действительно, из условий ковровости A a A b С A a + b и 2 A a A a + b С A 2a+b (условия (3) и (4) соответственно) вытекают включения PQ С P и соответственно 2 PP С Q . Так как P и Q поля char = 2 , то из последних двух включений, очевидно, следует равенство P = Q . Если char = 2 , то из условия ковровости A ² _a A _b С A _{2 a + b} получаются только включения P ² С Q С P. Отсюда, ковровая подгруппа Ф( A ) является промежуточной между группами Шевалле Ф(Q) и Ф(Р) над полями Q и соответственно P . Поэтому в силу леммы 5 ковер является замкнутым. Теорема доказана.