О несуществовании простого варианта полиномиального алгоритма извлечения корня из языка

Настоящую статью можно рассматривать как продолжение [1] . В ней (а также в более ранней статье [2] ) рассматривалась задача извлечения корня из заданного языка.

При этом корень — как и в других областях алгебры — является обратной операцией к операции возведения в степень и, также (так же) как и в других областях алгебры, определяется, вообще говоря, неоднозначно. При этом, конечно, последняя операция (возведение в степень) стандарнтым образом определяется через операцию умножения, которой в теории формальных языков обычно называют конкатенацию. Какой-либо пример неоднозначности извлечения корня легко конструируется даже для случая 1-буквенного алфавита: квадрат языка

B = {е, a, a2, a3, a4} равен

A = B2 = {е, a, a2,..., a7, a8}, и из языка A извлекается не только корень B, но и

B ' = { e, a, a ³ , a ⁴ } .

Повторим информацию, уже приведенную в [1] , более подробно. Несмотря на простоту формулировки задачи, автор не смог найти в литературе (а также в Интернете) какого-либо ее описания, в том числе даже ее постановки. Но, несмотря на это, возникает впечатление, что весь материал [1] и настоящей статьи является очень легким, и вызывает недоумение тот факт, что в известных автору монографиях нет хотя бы формулировок подобных задач.

Вообще, всюду в настоящей статье будет рассматриваться случай 1-буквенного алфавита и 2-й степени для корня; при этом на основе материала статьи [1] создается впечатление, что получаемые при таком упрощении результаты на более сложные ситуации обобщаются всегда ; но, конечно, строго доказать сформулированное в этом абзаце предположение вряд ли возможно.

Задачу извлечения корня можно рассматривать в нескольких вариантах (см. подробности далее) — но в статье будет рассматриваться задача построения за полиномиальное время хотя бы одного подходящего корня. При этом, конечно, всюду в настоящей статье полиномиальность понимается относительно размера входных данных — что в нашей ситуации можно считать суммарной длиной слов заданного языка (в примере выше — A).

Для формулировки результатов очень важно понятие «потенциальный корень» — и, в отличие от корня (являющегося языком), последний объект является словом: потенциальные корни нужной степени для заданного языка A — это те слова, у которых такая степень принадлежит языку A. Множество потенциальных корней строится за полиномиальное время; отметим, что это не очень сложное утверждение — однако тривиальным его назвать нельзя: алгоритмы, решающие эту задачу «в лоб», полиномиальными не являются, а полинмиальность похожих алгоритмов была показана, например, в [3] .

А экспоненциальные алгоритмы извлечения корня из языка описываются тривиальным образом : надо просто перебрать все подмножества множества потенциальных корней. К последнему стоит добавить, что при наличии проверяемого множества потенциальных корней — в литературе алгоритм его выбора часто называется оракулом, [4 –8] и др. — саму проверку того, является ли рассматриваемое подмножество корнем нужной степени, можно выполнить за полиномиальное время. Отметим еще, что в отличие от предыдущей проверки, полиномиальность этой проверки очевидна. Однако при этом надо осознавать, что степень полинома не может не зависеть от требуемой в задаче степени для извлечения корня.

Потенциальные корни используются и в другом классе задач — по-видимому, более сложном, чем задачи извлечения корня из языка. Это — задачи, которые условно можно назвать «раскодированием», или «построением инверсного морфизма», см. [3] и ссылки из этой работы. При этом, несмотря на б´oльшую сложность задач «раскодирования», описать полиномиальный алгоритм построения инверсного морфизма — при некотором специально сделанном предположении теории формальных языков, — в отличие от рассматриваемой здесь задачи извлечения корня из языка, уже удалось.

Итак, полный перебор всех подмножеств множества потенциальных корней (“brute-force algorithm”) считается невозможным. Но основным результатом статьи [1] была теорема о том, что если известен некоторый корень, то при выполнении специальных несложных условий к этому корню (как к подмножеству) можно добавить еще один потенциальный корень (как элемент); заранее отметим, что далее в настоящей статье будет приведено более подробное доказательство этой теоремы. Поэтому может возникнуть предположение, что можно осуществить следующую схему алгоритма:

\bullet некоторым образом описать все такие подмножества множества потенциальных корней, к которым заведомо нельзя добавить ни одного нового элемента (еще одного потенциального корня);

\bullet проверить все такие подмножества: не является ли какое-либо из них корнем, — и все это должно дать решение основной задачи (т. е. построение полиномиального алгоритма извлечения корня). Однако основной предмет настоящей статьи заключается в том, что подобные простые действия не могут привести к желаемому описанию полиномиального алгоритма, поскольку существуют примеры (и они ниже описаны), в которых число подмножеств, необходимых для подобной проверки, от размерности задачи зависит экспоненциально.

Но важно отметить, что при этом вовсе не утверждается несуществование полиномиального алгоритма извлечения корня: пока говорится лишь о том, что не может сработать подобный простой способ, то есть если и существует полиномиальный алгоритм решения рассматриваемой задачи, то в нем должна использоваться более существенная информация, чем та, которая формулирует возможность добавления нового элемента (потенциального корня) в некоторое подходящее под ответ множество потенциальных корней.

Отметим еще, что предмет настоящей статьи может быть охарактеризован и по-другому: в ней формулируются те утверждения, которые можно получить рассмотрением только таких пар потенциальных корней, оба элемента которых не могут одновременно входить в решение задачи.

Приведем содержание статьи по разделам. Раздел 1 — предварительные сведения и обо-значния, частично стандартные, а частично введенные ранее в предыдущих публикациях. Специальные обозначения, связанные с гиперкубами, вынесены в отдельный подраздел 1.2; там же приведены и соответствующие примеры.

В разделе 2 приводится дополненное доказательство теоремы о возможном увеличении одной координаты имеющегося корня: в опубликованном в [1] варианте доказательства этой теоремы не были рассмотрены все возможные ситуации.

Продолжение рассмотрения гиперкуба — применительно к N-мерному гиперкубу потенциальных корней — приведено в разделе 3. В основном, в этом разделе рассматриваются множество простых путей в этом гиперкубе — между «максимальной» и «минимальной» его вершинами. Уточняется формулировка гипотезы о множестве т. н. важных потенциальных корней.

В разделе 4 показывается возможность применение оптимизационных задач на графах — для решения некоторых подзадач, связанных с задачей извлечения корня из языка; в частности, рассматривается применение задачи 2-SAT.

Основные результаты статьи приведены в разделе 5: показана возможность конструирование примеров на тему несуществования простого алгоритма извлечения корня степени 2 — причем примеров для сколь угодно большой (но заранее известной) размерности; как и всюду в настоящей статье, простыми называются те алгоритмы, которые основаны лишь на информации о табуированных парах потенциальных корней.

В разделе 6 очень кратко рассмотрен частный случай для степени 3; при этом есть основания полагать, что на основе приведенного примера можно построить примеры для степени 3 сколь угодно большой (но, конечно, заранее известной) размерности — примеры, показывающие несуществование простого алгоритма извлечения корня 3-й степени.

В заключении повторены основные результаты статьи и приведены возможные направления дальнейших исследований по рассматриваемой тематике — описанию алгоритмов извлечения корня из заданного языка.

1.    Теоретическиие основы 1.1.    Общие обозначения

Приведем основные обозначения — частично стандартные, частично введенные ранее в [1] , а частично новые.

Смысл слова «умножение» для всех рассматриваемых объектов — обычный для теории формальных языков: это просто результат произведения (приписывания, конкатенации) двух слов (двух языков). Для иллюстрации рассмотрим такой пример для 1-буквенного алфавита — основного объекта настоящей статьи: если

C = { a i | i G I } и D = { a j | j G J }

(I и J — некоторые конечные подмножества целых неотрицательных чисел), то

C • D = { a ^k | ( 3 i G I, j G J ) ( k = i + j ) } .

Слово «умножение» будем в дальнейшем применять без кавычек: в нашем случае оно обладает не только обычными полугрупповыми свойствами (которые практически всегда необходимы при рассмотрении моделей теории формальных языков), но и, дополнительно к ним, коммутативностью.

Среди конечных подмножеств множества целых неотрицательных чисел, рассматривавшихся в предыдущем абзаце, особую роль будут играть множества вида

{ K,K + 1,...,L — 1,L } для некоторых K,L G N, L ^ K.             (1)

Множество вида (1) будем обозначать записью K, L.

На основе умножения (произведения) естественным образом определяется степень языка. Далее нам необходимо ввести описание операции извлечения корня — однако сначала зафиксируем несколько соглашений о терминах и о применяемых константах, которых будем всегда придерживаться при описании задач и рассматриваемых к ним примеров.

\bullet Первое соглашение. Всюду далее, если не сказано иного, решается задача поиска языка X, являющегося корнем уравнения

X 2 = A,                                    (2)

где язык A заранее задан. Отметим, что в [1] рассматривалось уравнение X M = A для различных M \geqslant 2, а в настоящей статье в разделе 6 кратко рассматривается случай M = 3.

\bullet При этом потенциальный корень — это некоторое слово u \in Σ ^\ast , такое что u ² \in A. В отличие от них (т. е. слов) — множество (язык) X будем называть корнем (без прилагательного «потенциальный»), если выполнено условие (2) . Как уже отмечалось, найти все потенциальные корни можно за полиномиальное время с помощью несложных алгоритмов.

\bullet Второе соглашение: N — количество потенциальных корней, будем их нумеровать от 1 от N; можно сказать, что здесь используется «обычная индексация Паскаля».

\bullet Третье соглашение. Если, как в приведенном во введении примере, «задача формируется» возведением во 2-ю степень некоторого языка (пусть это язык B; считаем что при решении получаем язык X), то представление этого языка (как множества, B или X) выполняем перечислением разрядов, от 0 до некоторого заданного n; здесь, наоборот, используется «индексация Си-подобных алгоритмических языков».

• •    Таким образом, размерность каждого из языков B и X равна n + 1 — и можно рассматривать только такие ситуации, когда и старший, и младший разряды равны 1. При этом 2 - n + 1 будет размерностью исходного языка A (т. е. для его задания нужно некоторым способом определить разряды от 0-го до 2n-го, причем также можно считать, что старший и младший разряды равны 1).

Для того, что выше названо «третьим соглашением», во всех случаях (т. е. как для A, так и для B / X) будут применяться 4 варианта обозначения множества слов:

\bullet во-первых, «самый обычный»: например,

{ £ = a 0 , a = a ¹ , aaa = a ³ , aaaaaa = a⁶ } .                     (3)

А остальные три варианта записи (см. далее, они описаны в виде примеров) будут применяться как для подмножеств множества потенциальных корней, так и для нескольких элементов множества

ε, a, aa, . . . a ^K-1 , a ^K

(при этом обычно будет либо K = n, либо K = 2n). Выше уже было сказано, что множество потенциальных корней считается зафиксированным, причем их число равно N. Будем также считать, что зафиксирована и их нумерация. Итак, приведем примеры других вариантов записи — для конкретного языка (3) :

• •    [ 0 13 6 ] — множество используемых степеней записываем в квадратных скобках в порядке возрастания;

\bullet 1001011 — двоичное число, в котором разряды предыдущего списка отмечены 1; разряды двоичного числа нумеруем начиная с 0 справа налево, каждые 10 разрядов (при наличии) отделяем небольшим пробелом;

\bullet 75 — число, принадлежащее \BbbN 0 , представляющее собой десятичную запись предыдущего пункта.

Как уже отмечалось, те же самые обозначения будут использоваться и для K = N, и при этом рассматриваются подмножества множества потенциальных корней; однако в этом случае разряды двоичного числа удобнее записывать слева направо и нумеровать начиная с 1. Например, пусть всего 5 элементов, а подмножество — { 2,5 } :

• •    [ 2 5 ] , иногда просто 2 5, даже иногда 25 — неоднозначности это не вызовет; пустое множество обозначается обычно, т. е. \varnothing;

\bullet 01001; пустым множеством здесь является последовательность нулей;

\bullet 9; пустое множество — 0.

Отметим, что что недоразумений (неоднозначности прочтения) в статье возникнуть не должно.

• 1.2.    Обозначения и примеры, связанные с гиперкубами

В нескольких приведенных выше варантах записи уже были использованы подмножества; при этом подмножества множества потенциальных корней (напомним, что ранее сделано предположение о том, что число их равно N) будем рассматривать как вершины N-мерного гиперкуба. Определим несколько связанных с подобным гиперкубом вспомогательных понятий.

• •    Определение максимальной вершины гиперкуба естественное — это ( 1,1,..., 1,1 ) .

\bullet Для дальнейшего — в случае рассмотрения задачи извлечения корня 2-й степени — часто будут использованы пары потенциальных корней; в частности, т. н. табуирован- ные пары (о них подробности далее). Для примера — если:

– принимается «третье соглашение» (напомним, что для него возможен только случай 1-буквенного алфавита)

— и при этом рассматривается множество [ 0 1 2 3 6 ] (оно действительно будет подробно рассмотрено в примерах в дальнейшей части статьи),

— а пара — { 2, 6} (конечно, порядок элементов пары несущественен), то возможны еще и такие обозначения этой пары:

– 2, 6 (это просто их по значениям); это то же самое, что и 6, 2 ;

— # 3, ^ 5 (это их по номерам, считаем номера начиная с 1).

• •    Для некоторой табуированной пары табуированная гиперплоскость — это такая N — 2-

• мерная гиперплоскость N-мерного гиперкуба, для которой обе координаты элементов пары равны 1.

\bullet Обобщением табуированной пары и табуированной гиперплоскости для степеней извлекаемого корня 3 более (продолжаем работать с 1-буквенным алфавитом) являются гиперплоскости соответствующих размерностей — но мы, однако, в настоящей статье подробно эти вопросы рассматривать не будем, это нужно только для примера, кратко рассматривающегося в разделе 6. Однако уже здесь стоит отметить, что в случае больши´х размерностей (пусть k) нужно рассматривать гиперплоскости не только размерности N—k, но и больших размерностей: среди элементов подмножества множества потенциальных корней, необходимого для формирования одного элемента исходного языка, могут быть совпадающие потенциальные корни.

\bullet Примеры обозначний для степени 3 —

^^^^     ^^^^

• 2,    5, 6 и 2, 6 .

В первом случае элементы, которых не должно быть в исходном языке — это

[ 6 9 10 12 13 14 16 17 18 ] ,

(поскольку каждый из элементов исходной табуированной тройки может входить в формируемую сумму более одного раза); а во втором случае —

[ 6 10 14 18 ] .

\bullet Отметим, что максимальная вершина этого гиперкуба входит в пересечение любого (ненулевого) количества любых табуированных гиперплоскостей — независимо от их размерностей (т. е. от размерности рассматриваемой задачи, иными словами — от степени извлекаемого корня).

\bullet На рисунках будем изображать гиперкуб «в обычном виде» в тех случаях, когда он приводится полностью; иначе (в частности, при больших размерностях) будем необходимую его часть изображать как подграф графа булеана.

• •    Для некоторой точки гиперкуба ( b 1 b ₂ .. .b _N ) обозначение ( b 1 b ₂ .. .b _N ) + k означает вершину, полученной из предыдущей путем замены k-й координаты на 1.

Перейдем к уточнению непосредственной постановки решаемой задачи. Как отмечалось в [1] (и ранее в [9] ), рассматривая для некоторого заданного конечного языка задачу извлечения корня заданной степени — либо максимально возможной степени — фактически имеется в виду не с одна задача, а целая группа задач , поскольку имеется несколько вариантов для требуемого ответа:

\bullet найти любой (корень из языка);

\bullet найти все

\bullet найти минимальный (по некоторой метрике),

\bullet и т. п.

Однако ниже всегда будет иметься в виду только задача построения любого корня.

Повторим рисунок из предыдущей статьи (ранее он был опубликован как [1, рис. 9]) — с некоторыми новыми комментариями.

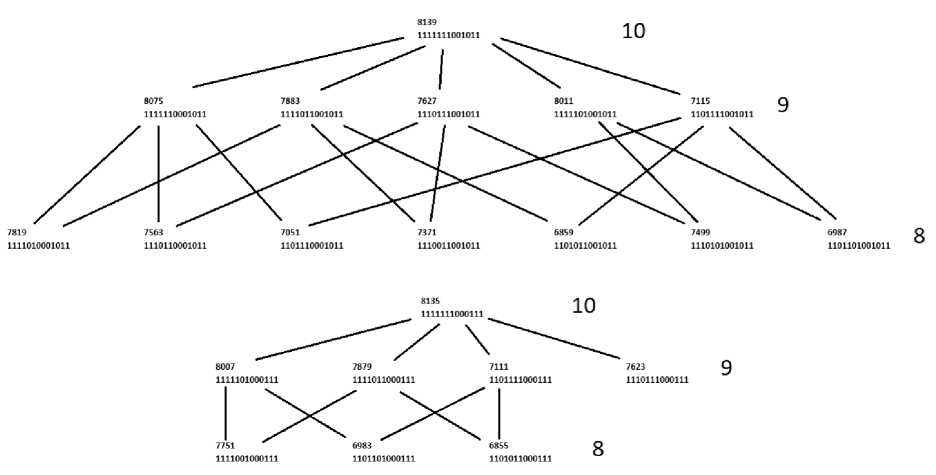
Рис. 1. Подграф графа булеана размерности 13

Как было сказано в [1] , на рисунке показан подграф графа булеана размерности 13 со всеми квадратными корнями квадрата слова

1101011000111 [ 0 1 2 6 7 9 11 12 ] ( 6855 ) .

Справа от элементов показаны уровни булеана — количества потенциальных корней, входящих (в качестве элементов) в рассматриваемый корень из языка. Сразу отметим, что всего существует С1з = 1287 вариантов подмножеств из 8 потенциальных корней, но лишь 10 из них являются квадратными корнями из заданного языка.

Также повторим в новых обозначениях пример с несколькими возможными корнями: у языка [ 01 2345678 ] имеется не только очевидный корень [ 0 1 2 3 4 ] , но и корень [ 0 1 3 4 ] . Понятно, что конструировать подобные примеры совсем несложно — гораздо сложнее обратная операция, о ней в настоящей статье и идет речь.

В заключение раздела отметим, что существуют примеры, когда (квадратные) корни есть — но ближайший к максимальной вершине корень находится от нее на сколь угодно большом (но заданном заранее) расстоянии. В [1] такой пример был приведен для расстояния 4 — но при этом был приведен с опечаткой, одна из форм записи рассматриваемого языка (квадрат которого и поступает на вход задачи) — это

[ 0 1 4 6 8 ]

(в [1] была опечатка: ошибочно было указано [ 0 2 4 7 8 ] , но при этом остальные возможные варианты записи рассматриваемого языка были приведены верно).

Более важно, что на основе такого примера для любого заданного L \in \BbbN можно построить пример языка, когда ближайший к максимальной вершине корень находится от нее на расстоянии L — в то время как общая размерность исходной задачи не превышает 2 \cdot L . Эти примеры очень простые, поэтому не будем приводить их общего описания (т. е. описания для произвольного заданного L), а рассмотрим только минимальный пример для следующего значения, L = 5 (как и ранее в [1] , минимальность понимается для исходного значения, взятого для возведения в квадрат — причем именно этот квадрат подается на вход рассматриваемой задачи). Итак,

\bullet язык, взятый для формирования примера, — 1363; в других вариантах записи его же получается

[ 0 1 4 6 8 10 ] или 10101010011 ;

тогда:

\bullet его квадрат (считаем именно его исходным языком для этой задачи) —

101010101111111110111     ( т.е. 1400823 );

• •    потенциальные корни — [ 0 1 2345678910 ] (т. е. все возможные значения в заранее известном промежутке, здесь — от 0 от 10), в другой записи — 2047.

2.    О возможном увеличении координаты имеющегося корня

Перебором на компьютере можно убедиться, что на расстояниях от максимальной вершины от 0 до 4 корней нет; ближайший корень — [ 0 1 4 6 8 10 ] , находящийся на расстоянии 5.

Вообще, приведенный ваше способ дает возможность конструировать такие примеры, в которых ближайший корень находится на любом заданном заранее расстоянии от максимальной вершины гиперкуба. При этом если расстояние должно быть равно L, то размерность примера (т. е. значение максимального потенциального корня) равна, как несложно убедиться, 2 \cdot L .

В этом разделе приводится дополненное доказательство теоремы о возможном увеличении одной координаты имеющегося корня. Вариант теоремы был опубликован в [1] — однако приведенное там доказательство нельзя назвать полным. Конкретно: с формальной точки зрения возможна такая ситуация, когда выбирается одно значение i1 (i в обозначени- ях приведенного в [1] доказательства) — в то время как условие k, i2 G Т(A) выполняется не для ii, а для некоторого i2 = ii. Понятно, что конкретных примеров в принципе привести невозможно — поскольку доказательство теоремы ведется от противного, т. е. показывается именно невозможность подобных ситуаций.

Теорема 1. Пусть

Пусть также для каждого i G 1, N \ { k } , такого что b i = 1, выполнено условие

^^^^

k, i G Т ( A ) .

Тогда

B+k = (b b2 . ..bN )+k также является корнем уравнения (2).

Доказательство. Очевидно, что B2 С ( B + k ) ² . Поэтому из выполнения неравенства ( B ₊ k ) ² = A следует обязательное выполнение условия ( B + k ) ² D A и существование по крайней мере одного разряда i G 1,N \ { k } , для которого выполнены следующие условия:

• • bi = 1,

3.    О путях в N-мерном гиперкубе потенциальных корней

bullet и при этом при возведении в квадрат у произведения появлялся бы новый разряд, равный 1 («новый» — отсутствовавший в B, т. е. принимающий в B значение, равное 0).

Отметим, что единственность такого значения i не утверждается, поэтому множество, состоящее из всех таких i, будет обозначаться как I.

А поскольку к B был добавлен только один разряд, а именно k-й, то последний факт возможен только при условии

(3 i G I)(1^ GT (A)) , что противоречит условию теоремы.                                                    \Box

В этом разделе рассматриваются вопросы, связанные с возможными путями в N-мерном гиперкубе потенциальных корней. Как и ранее, будем рассматривать 1-буквенный алфавит — хотя, как и многие вопросы настоящей статьи, материал этого раздела может быть обобщен на случай произвольного конечного алфавита. Отметим, что материал этого раздела связан с возможным описанием эвристических алгоритмов задачи извлечения корня из языка.

Итак, у нас есть N-мерный гиперкуб, каждая его точка (а их всего 2 ^N ) — это некоторое подмножество множества потенциальных корней. Придадим самим точкам следующие значения:

\bullet значение 1 — это корень (в примере на рис. 1 их всего 21);

\bullet значение 2 устанавливаем в том случае, когда квадрат этого языка включает в себя требуемый (исходный) язык как собственное подмножество ; отметим, что таковой (имеющей значение 2) должна являться максимальная точка гиперкуба, т. е. [ 1 N ] = ( 1,1,..., 1) — в противном случае рассматриваемая задача неинтересна:

– если это значение равно 1, то искомый корень известен;

– если это значение равно 0 (см. ниже), то и все значения вершин гиперкуба равны 0 и корней нет;

– значения, равного \varnothing (также см. ниже это обозначние), у максимальной точки гиперкуба быть не может — это несложно доказывается а основе введенных определений.

\bullet значение 0 устанавливаем в том случае, когда квадрат этого языка является собственным подмножеством требуемого (исходного) языка аналогично предыдущему пункту, таковой (имеющей значение 0) должна являться минимальная точка гиперкуба, т. е. [ 0 N ] = ( 0,0,..., 0 ) ;

\bullet значение \varnothing — оставшийся вариант: ни одно из рассматриваемых двух множеств (квадрат языка, соответствующего точке гиперкуба, а также исходный язык) не является подмножеством другого; отметим, что вариант совпадения этих множеств уже был рассмотрен: в этом случае значение равно 1, то есть это один из возможных корней.

Будем рассматривать все простые пути по ребрам гиперкуба из точки [ 1 N ] в точку [ 0 N ] ; отметим по этому поводу, что всего имеется N ! таких путей — поэтому вряд ли для какой-либо задачи представляют интерес варианты алгоритма, связанного с их полным перебором (brute force method).

У любого такого пути:

\bullet сначала несколько значений, установленных для вершин, равны 2;

\bullet затем, возможно , равны либо 1 либо \varnothing (одновременное включение в путь как 1, так и \varnothing, невозможно — этот факт можно несложно доказать аналогично сказанному выше;

\bullet в конце пути несколько значений равны 0.

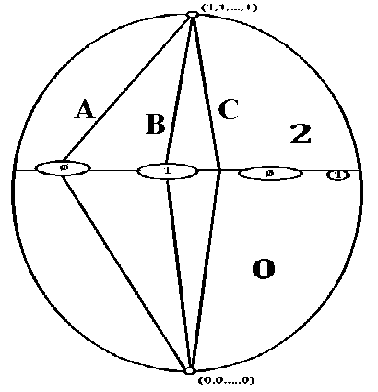
Рис. 2. Схема различных путей в графе булеана

На приведенном рис. 2:

\bullet при наличии вершин со значениями \varnothing путь помечен A;

\bullet при наличии вершин со значениями 1 путь помечен B;

\bullet при отсутствии вершин как со значениями \varnothing, так и со значениями 1, путь помечен C.

Далее будем рассматривать только пути вида C (если таковые имеются). Переход из значения 2 в значение 0, как и любое другое единичное движение, осуществляется удалением из рассматриваемого множества какого-либо из имеющихся в нем потенциальных корней; такой потенциальный корень (для которого существует хоть один подобный путь по вершинам гиперкуба) назовем важным . Заметим, что задача, заключающаяся в поиске всех важных потенциальных корней, конечно, может быть решена простым переборным алгоритмом (brute force method) — но в настоящей статье формулируется задача, заключающаяся в описании быстрых эвристических алгоритмов для нее.

В [1] была кратко сформулирована гипотеза, заключающаяся в том, что множество всех важных потенциальных корней (рассматриваемое как язык) — это один из корней из исходного языка. Пример, опровергающий эту гипотезу, может быть получен на основе модификации примера, приведенного на рис. 1. Действительно, как уже было отмечено, всего существует 1287 вариантов подмножеств из 8 потенциальных корней, но лишь 10 из них являются квадратными корнями из заданного языка. И можно считать, что горизонтальная линия на рис. 2, прерываемая несколькими овалами — подмножествами со значениями 1 и \varnothing, это и есть множество вершин гиперкуба, каждая из которых имеет ровно 8 таких координат, каждая из которых равна 1.

4.    О применении оптимизационных задач на графах

Рассматривавшийся выше в разделе 1.2 пример с 13 потенциальными корнями (в этом примере — все возможные значения в заранее известном промежутке от 0 от 12), по-видимому, малоинтересен:

\bullet в нем имеется только одно невозможное значение возможной суммы потенциальных корней (а именно, значение 5);

\bullet при этом, в отличие от материала следующего раздела, непонятно, как обобщить этот пример на произвольную размерность; отметим, что при возможном таком обобщении нам интерсны:

– во-первых, существование решения (в нашем примере оно есть),

• – и, во-вторых, линейная зависимость числа табуированных пар от размерности задачи.

В связи с этим рассмотрим сначала тривиальные определения, потом — построения, связанные с применением задачи 2-SAT, и уже после этого более сложный пример.

Итак, для очевидным образом определяемого графа табуированных пар , в котором:

\bullet множество вершин V является множеством потенциальных корней,

\bullet а множество ребер E соответствует всем табуированным парам.

Несложно убедиться, что такой граф является дополнением к графу, рассматривавшемуся в [1, разд. III], один из примеров приведен на [1, рис. 3].

Рассмотрим тривиальный пример графа табуированных пар — соответствующий языку, приведенному в разделе 1.2, см. рис. 3. Однако важно отметить, что тривиальным пример является с точки зрения материала настоящего раздела, а также с точки зрения теории графов вообще, — но, как уже понятно, не с точки зрения материала раздела 1.2.

Далее в N-мерном гиперкубе рассматриваются «нетабуированные» точки булеана — т. е. такие точки, в координаты которых не входит ни одна табуированная пара; стоит

1 0       2

|      | 6 7 8 9 10 11 12

5 4 3

Рис. 3. Очень простой пример графа табуированных пар отметить, что для каждой табуированной пары размерность получаемой «табуированной гиперплоскости» равна N — 2. На основе результатов теоремы 1 можно утверждать, что для поиска решения исходной задачи можно искать «нетабуированные» точки булеана, лежащие ближе всего к максимальной вершине. Решение — если хотя бы одно имеется — обязательно будет среди тех «нетабуированных» точек, для которых не существует соседней «нетабуированной», лежащей при этом ближе к максимальной вершине.

Однако простой подсчет даже при закреплении каких-то конкретных значений элементов табуированной пары дает общее число элементов табуированной плоскости 2 ^N-2 ; интуитивно понятно — даже без проведения точных подсчетов возможного числа соседних элементов — что подобное знчение вряд ли может дать полиномиальный алгоритм. И, по-видимому, такой подсчет вообще не может являться доказательством несуществованя простого (полиномиального) алгоритма, заключающегося именно в переборе точек, лежащих рядом (т. е. на расстоянии 1) с точками, соответствующими табуированным плоскостям. А следует такое несуществование из примеров, приведенных в разделе 5.

Дальнейшие построения связаны с формированием на основе графа табуированных пар задач дискретной оптимизации: задачи построения независимых множеств вершин графа (в том числе максимальных множеств), а также, в упрощенном случае, задачи 2-SAT — см. [7] и мн. др. При формировании соответствующих задач (2-SAT в первую очередь) отметим, что все входящие в получающуюся 2-КНФ переменные не содержат отрицаний. Поэтому возможный переборный алгоритм, сформированный на основе такой 2-SAT, представляет собой:

\bullet во-первых, поиск всех максимальных независимых подмножеств множества вершин V ;

\bullet и, во-вторых, рассмотрение всех точек N-мерного гиперкуба, соответствующих уменьшению какой-либо координаты какой-либо вершины одного из этих подмножеств.

Отметим, немного забегая вперед, что примеры следующего раздела показывают, что количество соответствующих вершин (необходимых для рассмотрения) может быть экспоненциально — относительно размера исходной задачи.

Рассмотрим более интересный пример. В качестве исходного языка выберем

[ 0 13 6 10 ];

квадрат этого языка ( входной язык рассматриваемой задачи) —

[ 01234679 10 11 12 13 16 20 ], множество потенциальных корней —

[ 0 1 2 3 5 6 8 10 ] .

Несложно получаемое множество табуированных пар сразу изобразим на графе, см. рис. 4.

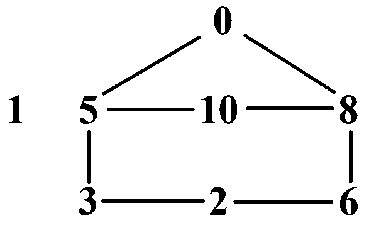
Рис. 4. Более сложный пример графа табуированных пар

Из предыдущего материала следует, что существуют две «максимальные» вершины N-мерного куба (т. е. такие вершины, увеличение любой равной 0 координаты которых приведет к появлеию хотя бы одной табуированной пары); они являются решениям как задачи построения максимального независимого множества вершин графа, так и задачи 2-SAT. Записи этих вершин приведем подробные (выше в настоящей статье такой способ записи не использовался), обозначая координату, соответствующую потенциальному корню q, записью x q .

Итак, координаты двух вершин следующие:

X o = 1, Х 1 = 1, X 2 = 0, X 3 = 1, X 5 = 0, X 6 = 1, X 8 = 0, X io = 1

и X o = 0, X i = 1, X 2 = 1, X 3 = 0, X 5 = 1, X 6 = 0, X 8 = 1, X io = 0.

Таким образом, в рассматриваемом примере для поиска «максимальных» корней достаточно проверить только 2 точки 8-мерного гиперкуба; первая из них в точности соответствует исходному языку, а вторая при проверке дает ошибку: квадрат построенного языка не равен языку исходному.

Важно, что в рассмотренном примере специально не отмечена разница между двумя оптимизационными задачами на графах, т. е. между 2-SAT и существенно более сложной задачей построения независимых множеств вершин графа. Причина такова. Основная цель получения необходимых условий для задачи извлечения корня заключается в том, чтобы на примерах показать невозможность краткого решения основной задачи, т. е. невозможность построения полиномиального алгоритма, использующего лишь информацию о табуированных парах потенциальных корней. А показать это можно и на очень простых графах — которые, однако, соответствуют экспоненциально большому числу вершин гиперкуба, которые необходимы для перебора; см. следующий раздел.

А в завершение этого раздела приведем очевидную формальную запись задачи 2-SAT — которая выше фактически была решена; для входящих в задачу переменных будем пользоваться теми же обозначениями.

( X o | X 5 ) & ( X 5 | X 3 ) & ( X 3 | X 2 ) & ( X 2 | X 6 ) & ( X 6 | X ₈ ) & ( X 8 | X o ) & ( X 5 | X io ) & ( X io | X 8 ) .

Понятно, что реальные примеры решения задачи построения независимых множеств вершин графа существенно сложнее, чем приведенные в этом разделе. Однако нам нет необходимости рассматривать такие более сложные примеры: нам достаточно существование таких примеров, в которых при рассмотрении только решения 2-SAT требуется перебор вершин N-мерного гиперкуба, число которых от размерности задачи зависит экспоненциально; это сделано в следующем разделе.

5.    Примеры про несуществование простого алгоритма: сколь угодно большая размерность для степени 2

В этом разделе приведены основные результаты статьи: показана возможность конструирование примеров на тему несуществования простого алгоритма извлечения корня степени 2 — причем примеров для сколь угодно большой (но заранее известной) размерности; как и всюду в настоящей статье, простыми здесь считаются алгоритмы, основанные только на информации о табуированных парах потенциальных корней.

Для осуществления описания подобных примеров возникают следующие вопросы. Первый, более простой (но, видимо, неочевидный) — про существование описания задачи, для которой построенное число «максимальных» точек от размерности этой задачи зависит экспоненциально . Второй, более сложный, — когда дополнительно к этому сформулированная таким образом задача должна иметь решение (т. е. для заданной задачи корень нужной степени должен извлекаться). Описанный в этом разделе пример (на самом деле — целое семейство примеров) дает положительный ответ сразу на оба эти вопроса.

Итак, сначала рассмотрим следующий пример. Исходный язык такой:

[ 0 1 3 5 8 9 10 ], его квадрат (заданный, входной язык) —

[ 0 1 2 3 4 5 6 8 9 10 11 12 13 14 15 16 17 18 19 20 ] = 0,6 U 820

(т. е. все значения от 0 до 20, за исключением 7), язык потенциальных корней —

[ 0123456989 10 ] = 0JO

(т. е. все возможные значения для рассматриваемой размерности входного языка, равной 20), в наших обозначениях N = 11. Формулировку задачи можно изобразить в виде таблицы, приведенной на рис. 5.

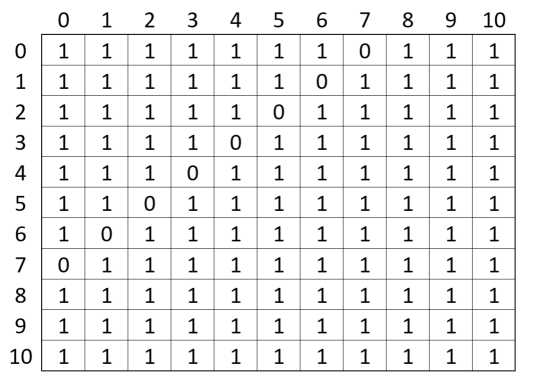
Рис. 5. Возможная формулировка задачи для M = 2, n = 10

А решение задачи — фактически приведенное выше в качестве исходного языка — можно изобразить в виде таблицы, приведенной на рис. 6; в ней (в ее клетках) имеются все числа от 0 до 20, кроме 7.

О 1   3   5   8   9 10

0	1	3	5	8	9	10
1	2	4	6	9	10	11
3	4	6	8	11	12	13
5	6	8	10	13	14	15
8	9	11	13	16	17	18
9	10	12	14	17	18	19
10	11	13	15	18	19	20

Рис. 6. Решение приведенной задачи для M = 2, n = 10

В рассмотренном примере граф табуированных пар содержит ребра

<^'^<' ^^^^ <^^Х ^^^'.

0,7, 1,6, 2,5, 3,4 , которые удобно обозначать так же, как и сами пары. Итак, если размерность входной задачи считать равной 20 (что естественно), то число этих ребер равно 4 = 240 — 1. Поэтому число «максимальных» точек N-мерного гиперкуба (как уже было отмечено, в рассматриваемом примере N = 11), необходимых для проверки наличия корня, равно 24 = 16:

\bullet для 3 координат 11-мерного гиперкуба, не входящих в табуированные пары, нужно установить значения 1 (иначе будет нарушено требование максимальности для формируемой точки гиперкуба),

\bullet а для остальных 4 пар координат (отметим, что каждая координата входит в единственную табуированную пару) нужно рассмотреть по 2 возможности (пары значений (0,1) и (1,0)), которые можно устанавливать независимо от остальных значений пар.

Покажем, как для ранеее использованного обозначения n (в примере выше было n = 10) получать необходимые примеры решаемых задач при задании больших значений n. Для простоты будем считать n четным, причем n ^ 10; пусть n = 2q. Входными языками примеров будут

0, n — 4 U n — 2,2n.

Для некоторого конкретного n = 2q граф табуированных пар содержит ребра

{ 0,n—3, 1,n—2 ..., q—3, q, q— 2 q—1 } , причем только их; всего таких ребер q — 3. Поэтому в получаемых примерах для любого выбранного четного n \geqslant 10 из-за независимости рассмотрения пар существует

2 ^{n 2-3}                                                         (4)

вариантов значений точек n + 1-мерного гиперкуба, необходимых для переборного поиска решения — в случае, когда такой поиск основан только на информации о табуированных парах.

6.    Пример для степени 3

Совершенно аналогично [1, разд. VIII], здесь частный случай для степени 3 рассматривается очень кратко; однако есть основания полагать, что:

\bullet во-первых, на основе приведенного далее примера можно построить примеры для степени 3 сколь угодно большой (но, конечно, заранее известной) размерности — примеры, показывающие несуществование простого алгоритма извлечения корня 3-й степени 1 ;

\bullet во-вторых, примеры обобщаются и на произвольную степень M > 3.

Итак, пусть исходное множество степеней буквы таково:

[ 0 1 4 7 10 16 17 18 ] .

На его основе приведем разложения чисел от 0 до 54 в виде суммы трех чисел, входящих в исходное множество (если вариантов несколько, то приводим только один):

0 = 0 + 0 + 0	1 = 0 + 0 + 1	2 = 0 + 1 + 1	3 = 1 + 1 + 1	4 = 0 + 0 + 4
5 = 0 + 1 + 4	6 = 1 + 1 + 4	7 = 0 + 0 + 7	8 = 0 + 1 + 7	9 = 1 + 1 + 7
10 = 0+0+10	11 = 0+1+10	12 = 1+1+10	13 ...	14 = 0+4+10
15 = 1+4+10	16 = 0+0+16	17 = 0+0+17	18 = 0+0+18	19 = 0+1+18
20 = 0+10+10	21 = 1+10+10	22 = 0+4+18	23 = 1+4+18	24 = 4+10+10
25 = 0+7+18	26 = 1+7+18	27 = 0+10+17	28 = 0+10+18	29 = 1+10+18
30 = 10+10+10	31 = 7+7+17	32 = 7+7+18	33 = 0+16+17	34 = 0+17+17
35 = 0+17+18	36 = 10+10+16	37 = 10+10+17	38 = 10+10+18	39 = 1+10+18
40 = 4+18+18	41 = 7+17+17	42 = 7+17+18	43 = 7+18+18	44 = 10+17+17
45 = 10+17+18	46 = 10+18+18	47 . . .	48 = 16+16+16	49 = 16+16+17
50 = 16+16+18	51 = 17+17+17	52 = 17+17+18	53 = 17+18+18	54 = 18+18+18

Таким образом в рассмотренном примере получаются 2 «пропущенных» значения для входного языка — что дает основания предполагать возможность описать на основе этого примера примеров сколь угодно большой размерности для этой же степени 3. Однако оценок, аналогичных (4) , мы в настоящей статье делать не будем.

Заключение

Итак, в настоящей статье заканчивается рассмотрение тех вопросов, связанных с извлечением корня 2-й степени из языка над 1-буквеным алфавитом, которые можно получить на основе одних лишь табуированных пар потенциальных корней. В частности, мы показали, что на основе информации лишь о потенциальных корнях — и рассмотрении специальных вершин гиперкуба потенциальных корней — нельзя построить полиномиальный алгоритм извлечения корня из языка. Однако при этом не утверждается несуществование такого алгоритма: возможно, такие алгоритмы и существуют, но они долждны получаться на основе более полной информации об исходной задаче.

В качестве одного из направлений развития темы, рассмотренной в настоящей статье, укажем связь между рассмотренными выше вершинами гиперкуба потенциальных корней (0, 1, 2 и \varnothing) — и практически такими же обозначениями, применявшимися в нескольких относительно недавних статьях Г. Г. Рябова 2 для задач, связанных с ДНФ и проблемами их минимизации; упомянем статьи [10–12]. На вершинах гиперкуба потенциальных корней, как и на т. н. кубантах в этих статьях, может быть построена специальная алгебра, которую можно использовать в дальнейших построениях и задачах — как чисто теоретических, так и вычислительных.

Работа частично поддержана грантом научной программы китайских университетов “Higher Education Stability Support Program” (раздел “Shenzhen 2022 — Science, Technology and Innovation Commission of Shenzhen Municipality”).