О новом подходе к разработке математической модели формирования поверхности детали при выполнении операции вибрационной очистки
Автор: Бабичев Анатолий Прокофьевич, Мишняков Николай Тимофеевич, Эссола Дьедонне
Журнал: Advanced Engineering Research (Rostov-on-Don) @vestnik-donstu
Рубрика: Краткие сообщения
Статья в выпуске: 3 (64) т.12, 2012 года.
Бесплатный доступ
Рассмотрены вопросы, связанные с математическим описанием модели формирования поверхности детали при вибрационной очистке. Приведены расчеты вероятности того, что определенная точка внутри конкретной площади была очищена, а также математическое ожидание случайной площади детали частицами обрабатывающей среды.
Вибрационная обработка, деталь, обрабатываемая поверхность, математическая модель, поверхностный слой
Короткий адрес: https://sciup.org/14249833
IDR: 14249833 | УДК: 621.9.048.6
On new approach to developing mathematical model of workpiece surface forming under vibration cleaning
The issues on the mathematical description of the workpiece surface forming pattern generation under the vibration cleaning are considered. The probability that the predetermined point within the specific area has been cleaned is calculated. The mathematical expectation of the workpiece random area by the particles of the processing medium is presented.
Текст краткого сообщения О новом подходе к разработке математической модели формирования поверхности детали при выполнении операции вибрационной очистки
Введение. Вибрационная обработка (ВиО) охватывает широкий спектр технологических операций -отделочно-зачистные, моечные, упрочняющие, покрытия и др. [1].
В ряде работ рассмотрены математические модели формирования поверхности и поверхностного слоя при выполнении некоторых операций ВиО [2]. В излагаемой статье рассматривается вариант подготовки решения такой задачи на основе представления обрабатываемой поверхности в виде фиксированного круга, покрываемого случайными кругами.
Математическая модель формирования поверхности детали. Предположим, что имеется N кругов радиусом а и что их центры независимо и равномерно распределены по области, состоящей из всех точек плоскости, расстояния до которых от круга радиусом R (назовем его Л) не превышают a.
Случайное множество X определяется как общая часть круга А радиусом R с теоретико-множественным объединением N кругов радиусом а. Площадь Т равна ^(Л + я)2, а площадь каждого круга С равна ла2 . Вероятность того, что любая точка внутри А покрывается одним кругом С, равна:
а
Р = ~---7^ ^ = 7--- л^К + а^ ^R + a^
Вероятность того, что любая точка внутри А покрывается по крайней мере одним кругом С, равна р^М(х>Х^Ц1-р^ =1- —-— .
ЦЛ + а) )
М(8) =
Математическое ожидание случайной величины площади S, покрытой хотя бы одним кругом С, равна
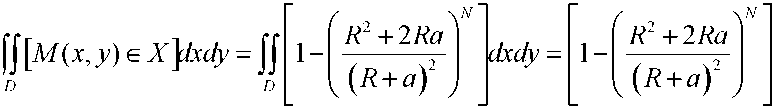
лК2
где D - область внутри круга радиусом А.
Итак,
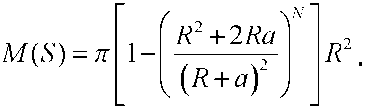
Для получения второго момента Л/(52) рассмотрим внутри А две точки: Рх и Р^.
Вероятность того, что ни одна из этих точек не окажется покрытой, равна qN(r), где q(r) есть доля Т, лежащая вне объединения кругов радиусом а с центрами в Рх и Р2. По скольку Рх и Р^ лежат в круге А, эта доля зависит только от г (расстояния между Рх и Р2\ Очевидно, 0 R M(S2) = I*qN(r)(p(r)dr. (3) о Обозначим через Q(r) площадь пересечения двух кругов радиусом а, центры которых разделяет расстояние г. Тогда О, если г >- 2а; Q(r) = j 2а2(0-sin9cos0), если г <2а. где 9 = arccos ,a y(r) = 1-2/2 + v л^Р + а) лР2 + ла2 + Q(r) л^Р + а) To есть л(р2 + аЛ + Р1(г) ^) = ——;—— ' л(Р + а) где r = 2Rcosa; a- arccos — Выводы. Предложенная математическая модель процесса ВиО плоского круга R частицами обрабатывающей среды в заданных допущениях позволяет вычислить вероятность того, что любая точка внутри А покрывается одним кругом С (формула (1)), а также определить среднее значение площади круга R, покрытой хотя бы одним кругом С (формула (2)), и второй момент M^S2^ обработанной площади круга R (формулы (3), (4)) [2-4]. С учетом полученных результатов возможно определение продолжительности вибрационной обработки детали при заданных параметрах. Методика и уравнения расчета продолжительности обработки представлены в работах [5, 6].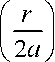
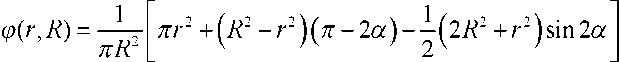
Список литературы О новом подходе к разработке математической модели формирования поверхности детали при выполнении операции вибрационной очистки
- Бабичев А.П. Основы вибрационной технологии/А.П. Бабичев, И.А. Бабичев; изд. 2-е, перераб. и доп. -Ростов н/Д: Издательский центр ДГТУ, 2008. -694 с.
- Кендаля М. Геометрические вероятности/М. Кендаля, П. Моран. -М. Наука, 1972.
- Бабичев А.П. Определение среднего значения площади обработанной плоской детали при виброобработке в случае наиплотнейшей упаковки/А.П. Бабичев, Н.Т. Мишняков//Вопросы вибрационной технологи: межвуз. сб. науч. тр. -Ростов н/Д, 2003.
- Бабичев А.П. К расчету некоторых параметров вибрационной обработки на основании теоретико-вероятностной модели процесса/А.П. Бабичев, Н.Т. Мишняков//Вопросы вибрационной технологии: межвуз. сб. науч. тр. -Ростов Н/Д, 1999.
- Бабичев А.П. Решение вопросов продолжительности виброобработки по новой теоретико-вероятностной схеме процесса виброобработки/А.П. Бабичев, Н.Т. Мишняков//Отделочно-упрочняющая механическая обработка, качество поверхности и эксплуатационные свойства деталей машин: сб. статей/РИСХМ. -Ростов н/Д, 1978.
- Бабичев А.П. Определение площади множества точек на плоскости, образованных ровно т кругами радиуса r (на примере вибрационной обработки)/А.П. Бабичев, Н.Т. Мишняков//Вопросы вибрационной технологии: межвуз. сб. науч. ст. -Ростов Н/Д: Издательский ДГТУ, 2007 -С.109-110.
