О новых возможностях метода эллипсометрии, обусловленных "нулевой" оптической схемой. Эллипсометрия реальных поверхностных структур. 6. Эллипсометрия многослойных поглощающих систем. Основные положения

Основной целью настоящей работы является рассмотрение общих положений эллипсометрии поглощающих сред, непосредственно связанных с решением обратной задачи. Сюда относятся:

• •    исследование углов полной поляризации для однослойной системы с поглощающей пленкой произвольной толщины;

• •    подробное рассмотрение основного уравнения эллипсометрии для N -слойной системы с выделенным произвольным j -м слоем, базирующегося на использовании рекуррентных соотношений;

• •    обобщение метода Холмса на случай многослойных сред;

• •    общая характеристика метода решения обратной задачи эллипсометрии для многослойных поглощающих систем, включающего в себя новые критерии выбора оптимального решения, основанные на использовании основных формул обобщенного на N -слойные системы метода Холмса.

• 1 . ОБ ОСОБЕННОСТЯХ ПОВЕДЕНИЯ УГЛОВ ПОЛНОЙ ПОЛЯРИЗАЦИИ ДЛЯ СЛУЧАЯ ПОГЛОЩАЮЩЕЙ ПЛЕНКИ ПРОИЗВОЛЬНОЙ ТОЛЩИНЫ НА ОДНОРОДНОЙ ПОДЛОЖКЕ

В предыдущей работе [1] на основе предложенного общего подхода изучены основные закономерности в поведении углов полной поляризации для однослойной поглощающей отражающей системы. Предложена также схема, на основе ко- торой легко доказывается, что поляризационный угол А на углах полной поляризации ф0 = ф0p(s) при соответствующих значениях толщины пленки, как и в случае прозрачных сред, испытывает скачок величиной 180°, т. е. имеет вид ступеньки

А ( Ф о p ( , ) — 0) = 180 ° , А ф p ( , ) + 0) = 0(360 ° ), (1) причем при любых значениях коэффициентов поглощения подложки и пленки, при которых углы полной поляризации еще существуют. Сохраняется также при появлении поглощения и характер поведения угла А в процессе перехода (при увеличении толщины пленки) от одного вида ступеньки высотой 180 ° к другому (от нижней к верхней или наоборот) [2].

Случай "поглощающая подложка—прозрачная пленка" на первый взгляд практически не отличается от случая прозрачной системы [2]. Прежде всего это относится к сохранению факта периодичности по толщине пленки с периодом D ₀ эффекта полной поляризации и самих поляризационных углов А и Т . В то же время для данной системы наблюдается огромное разнообразие в зависимостях А ( ф ₀) и Т ( ф ₀), обусловленное дополнительным и очень сильным влиянием коэффициента поглощения подложки к ₀ на поведение углов полной поляризации ф ₀ p и ф ₀ s , определяемых уравнениями [1]

F p ( ф 0 ) = 0, F s ф) = 0. (2)

Функции F p ( ф ₀) и F s ( ф ₀ ) зависят, очевидно, и от оптических постоянных подложки ( n ₀, к ₀), и пленки ( n 1 , к 1 ). С увеличением к ₀ (при заданных n ₀, п 1 и к , = 0) кривые F p ₍ s) ( ф ₀), определенные на угловом интервале (0,90 ° ), смещаются вниз. Происходит это в основном за счет смещения вниз крайнего левого конца кривых, т. е. за счет уменьшения значения F p ₍ s ) (0) (подробнее см. [1]). Все это сказывается не только на количестве и поведении углов ф ₀p ( s ) . От к ₀ очень сильно зависят и значения толщины пленки, при которых реализуются углы полной поляризации. Именно это и определяет интерес к системе "поглощающая подложка—прозрачная пленка".

Особый интерес представляет случай поглощающей пленки на прозрачной или поглощающей подложке. Для поглощающей пленки функции Fp (ф0) и Fs (ф0) зависят также и от целого числа m, определяющего максимальное число полных периодов D0, содержащихся в толщине пленки d 1 [1]. Последовательно увеличивая m начиная от значения m = 0 и проверяя при этом уравнения (2) на наличие решений, устанавливаем то значение m = m 0, при котором первый раз не проявляется ни один из углов полной поляризации (ни одно из уравнений (2) не имеет решения). Определим период, в котором находится толщина пленки d1 , интервалом

( mD U m + 1) D 0 ), ( m = 0,1,2,...), (3) где ( m + 1) определяет номер периода (номер соответствующего интервала (3)), начинающийся со значения 1. Тогда можно сказать, что самый нижний период (нижний интервал) для d 1 , начиная с которого не проявляются углы полной поляризации, определится как ( m ₀ + 1)-й период

( m 0 D 0 ,( m 0 + 1) D 0 ). (4)

Это, очевидно, означает также, что самым верхним периодом, в котором еще определяются углы полной поляризации, будет m ₀ -й период, определяемый интервалом (( m ₀ - 1) D ₀, m ₀ D ₀). Если m ₀ = 0, то, следовательно, углы ф ₀ p ₍ s ) не проявляются ни в одном периоде.

Для устранения некоторой неопределенности необходимо сделать уточняющее замечание относительно интервала (3), определяющего (m + 1)-й период. Величина D0 , а значит, и интервал (3) зависят от угла падения ф0 , т. е. заданная толщина пленки d1 при изменении ф0 может принадлежать периодам с разными номерами. Однако принадлежность d 1 (m + 1)-му периоду означает здесь совсем другое. При заданном номере периода уравнения (2) определяют углы ф0p(s), а еще одно уравнение (см. [1]) — отвечающие им значения толщины d 1 p(s) [1]. И вот эти значения d 1 p(s) как раз и принадлежат периодам (интервалам) (3), которые всегда определяются одним и тем же заданным номером и соответствующими и разными фоp(s). Это можно выразить соотношением d 1 p(s) Е (m D0 (ф0p(s))> (m + D D0 (ф0p(s) )) (5)

(см. также соотношения (13), приведенные ниже).

Описание поведения углов полной поляризации для случая однослойной системы с поглощающей пленкой, данное в работе [1], носит слишком ограниченный характер и связано прежде всего с предельным переходом d 1 ^ ^ ( m ^ ” ). В частности, замечание относительно невозможности определения из уравнения F p ( ф ₀) = 0 угла Брюстера для прозрачной подложки, на которой находится поглощающая пленка, также связано с отличными от 0 значениями m ( m >  0). Таким образом, есть необходимость дать более общее и, по возможности, детальное описание поведения углов полной поляризации ф ₀ p _{( s} ) для системы с поглощающей пленкой.

Рассмотрим сначала ситуацию, когда поглощением обладает только пленка, т. е.

к 0 = 0, к 1 > 0. (6)

Здесь, в первую очередь, обращает на себя внимание следующее обстоятельство. Если в предыдущем случае прозрачной пленки на поглощающей подложке с увеличением к ₀ кривые F p ( s ) ( ф ₀) смещаются вниз, то в данном случае, определяемом условиями (6), те же кривые с увеличением уже к ₁ смещаются, наоборот, вверх (опять-таки за счет увеличения значения F p _{( s} ) (0)). Однако здесь есть одна особенность, связанная с зависимостью функций F p _{( s} ) ( ф ₀) от числа m . В связи с этим данные функции и соответствующие уравнения будем представлять в более общей форме:

F p ( s ) ( ф 0 , m ) = 0, m = 0,1,2,..., m 0 - 1. (7) При этом углы ф _{0 p} ( _s ) , следующие из уравнений F p ( s ) ( ф ₀, m ) = 0, и отвечающие им толщины d 1 _{p ( s} ) относятся к ( m + 1)-му периоду (интервалу (3)).

При m = 0, когда толщина пленки d 1 принимает любое значение в пределах первого периода начиная от 0, уравнение F p ( ф ₀, 0) = 0 определит угол Брюстера ф ₀ b для прозрачной подложки, а соответствующая формула из работы [1] покажет, что этому углу отвечает нулевая толщина пленки ( d 1 = 0). Это очевидный результат, но важно, что он следует из уравнения (7) (при m = 0) при любых оптических параметрах поглощающей пленки. Отсюда вытекает и специфика в поведении кривой F p ( ф ₀, 0). При увеличении k кривая F p ( ф о , 0) действительно смещается вверх, но так, что при любом k _j она пересекает ось ф ₀ в двух точках, определяющих углы p -типа ф _{0 p} :

ф 0 = ф 01 p = ф 0 b и ф 0 = ф 02 p .

Первая из этих точек, представляющая угол Брюстера, остается неподвижной, а вторая с ростом k ₁ приближается к углу Брюстера ( ф _{02 p} ^ ф ₀ b ) Это означает, что точка минимума кривой F_p ( ф ₀, 0) приходится на интервал ( ф ₀ b ф _{02 p} ), а сам минимум кривой поднимается при k _j ^ ^ к оси ф ₀, но всегда остается ниже этой оси.

Кривая F s ( ф ₀,0) ведет себя иначе. Пусть при некоторых k <  k j⁰⁾ она пересекает ось ф ₀, что означает существование угла полной поляризации s-типа ф _{0 s} . Если k _j увеличивается, проходя значение kj ° , то кривая F s ( ф ₀,0) буквально поднимается над осью ф ₀, нигде не пересекая и не касаясь ее. В этом случае начиная с kj^o) угол ф _{0 s} перестает существовать. Ему на смену приходит второй угол p -типа ( ф _{02 p} ), и возникает описанная выше картина с кривой F_p ( ф ₀, 0).

Таким образом, при m = 0 независимо от оптических параметров поглощающей пленки на прозрачной подложке углы полной поляризации не исчезают. А это означает, что для системы "прозрачная подложка—поглощающая пленка" всегда m ₀ >  0.

Совсем иначе ведет себя кривая F_p ( ф ₀, m ) для той же отражающей системы, но при m >  0 . При заданном m >  0 и росте k ₁ , как и при заданном k ₁ и росте m , эта кривая поднимается вверх, так что в конце концов полностью оказывается над осью ф ₀. Точно так же ведет себя и кривая F s ( ф ₀, m ), но это проявляется, как указано выше, уже при m = 0.

Рассмотрим теперь самую общую ситуацию, когда поглощающими являются и пленка, и подложка к0 > 0, kj > 0. (8)

В данном случае коэффициенты поглощения подложки ( к ₀) и пленки ( k _j) в своем влиянии на кривые F_p ( ф ₀, m ) и F s ( ф ₀, m ) играют противоположную роль. По этой причине можно ожидать новых результатов. При m = 0 уравнение F_p ( ф ₀, 0) = 0 определит эффективный угол Брюстера ф _{0 Ьэ} ф и, если уравнение F s ( ф ₀, 0) = 0 не определяет угол ф _{0 s} , еще один угол p -типа ф _{02 p} . С ростом k _j (при фиксированных n ₀, к ₀ и n _j) кривые F_p ( ф ₀,0) и F s ( ф ₀ , 0) поднимаются вверх. При этом сначала кривая F s ( ф ₀ , 0) перестает пересекать ось ф ₀ (если при k = 0 она ее пересекала), оказываясь над ней, а затем и кривая F_p ( ф ₀, 0), пересекая вначале (после подъема ^Fs ( ф 0 , ^{0) )} ось ф 0 в точках ф 01 p = ф 0 Ьэф и ф 02 p , под нимается над осью. В результате при определенном значении к ₁ углы полной поляризации перестают существовать. Это означает, что для системы, определяемой условиями (8), предельное число может принимать значение m ₀ = 0.

Рассмотрим теперь зависимость предельного числа m ₀ от коэффициента поглощения к ₁ пленки, имея в виду широкий диапазон изменения к ₁ . Совершенно очевидно, что число m ₀ растет с уменьшением k _j, точнее: при k _j ^ 0 m ₀ ^ ^ . Введем функцию m ₀ ( k _j) и опишем ее поведение.

При монотонном увеличении к ₁ от некоторого малого значения к ₁ ⁽⁰⁾ предельное число m ₀ последовательно и скачкообразно уменьшается на 1. Иными словами, существует возрастающая последовательность

л⁽⁰⁾ £^(j) к)¹ ) kN^N ) 191 k j , k j , ... , k j , ... , k j , ⁽⁹⁾

на каждом элементе которой m ₀ уменьшается на 1

m0(kj1) + 0) = m0(kj( 1) - 0) - 1, (10) а в каждом 1 -м интервале (kj1 -j), кj1)) (1 = 1, 2, ... , N) m0 остается постоянным, причем m0(kj1 -j) + 0) = m0(kj1) -0). (11)

При этом важно отметить, что величина 1-го интервала Skj1) = kj1) - kj1 -j) с возрастанием индек- са i увеличивается. Заметим также, что последний элемент kjN) последовательности (9) является предельным, т. е. для любого k1 > kjN) имеем m 0 (kj) = m 0 (kj N) + 0) = 0 или 1.

Введем величины 3р _{0 p} и 3 d _{j p} , представляющие собой разности углов полной поляризации р ₀₂ p и р _{01 p} и отвечающих им толщин пленки d j²_р ^{и d} p ^:

³Р 0 p ⁽ k j , ^j — ^j) >  ³Р 0 p ⁽ k j , ^j X 3 d j p ( k j , j - 1) >  3 d j p ( k j , j ),

j = m 0 ( i ),..., 3,2.

При j >  m ₀ ( i ) углы полной поляризации уже не проявляются, и величины (j2) теряют смысл.

2. ОСНОВНОЕ УРАВНЕНИЕ ЭЛЛИПСОМЕТРИИ ДЛЯ N -СЛОЙНОЙ СИСТЕМЫ С ВЫДЕЛЕННЫМ ПРОИЗВОЛЬНЫМ СЛОЕМ

³Р 0 p ⁽ k j , ^j ) = Р 02 p ⁽ k j , ^j ) - Р 01 p ⁽ k j , ^j X

³ d J p ( k j , j ) = d J^{( 2}p ( k j , j ) - d Ip ) ( k j , j ).

Все величины в (12) зависят от коэффициента k _j и номера периода j (см. рассуждения, связанные с

формулами (3) и (4)); в частности, для и d™ имеют место соотношения d£ (kj, j)e ((j-1)D0(Р01 p), jD0Р01 p)), d 1(?(k1, j)e ((j — 1)D0(Р02p), jD0Р02p)).

d j⁽ p ²⁾

Предполагая, что k _j принадлежит i -му интервалу, определимся и с величинами j и m ₀:

k j e ( k j ' ^{- j)} , k j ' ) ),     m 0 = m „ ( k j ) = m 0 ( i ),

1 < j < m0('X

В пределах j -го периода уравнения (7), определяющие P 0J p ( k j , j ) и р 02 p ( k j , j ), приобретут соответствующий вид, если в них положить m = j - 1.

Представляет интерес поведение величин (j2) для случая предельного верхнего периода с номером j = m ₀ ( i ). Величины 3р _{0 p} ( k _j, m ₀ ( i )) и 3 d _{j p} ( k _j, m ₀( i )) достигают некоторых максимальных значений на левом конце ( k j ' ^{- j)} + 0), а с возрастанием k _j уменьшаются, обращаясь в ноль на правом конце ( k j ' ) - 0) i -го интервала. Можно еще сказать, что при прохождении возрастающей последовательности (9) на каждом ее i -м элементе величины 3р _{0 p} и 3 d _{j p} испытывают скачок от 0 (в конце i -го интервала) до некоторых значений (в начале i + 1-го), причем, высота скачка для каждой из этих величин увеличивается с ростом индекса i .

Снова рассмотрим величины (12) для любого заданного k _j из i -го интервала, но уже для периодов с номерами j <  m ₀ ( i ). Здесь следует отметить, что с уменьшением номера периода j эти величины увеличиваются:

Основное уравнение эллипсометрии для N -слойной отражающей системы, приведенное в работах [2, 4], уже содержит выделенный слой, причем в одном случае это верхний ( N -й) слой [2, 4], в другом же выделенным является произвольный j -й слой [4]. Эти уравнения построены на использовании простых рекуррентных соотношений, позволяющих легко описать любую многослойную систему. Данные рекуррентные соотношения, записанные в работах [2, 4] без вывода, первоначально были получены на основе результатов работы [5], в которой установлена закономерность перемножения любого количества матриц однородных слоев и найдены выражения для элементов полной матрицы N -слойной системы. Однако такой путь довольно сложен, и мы не будем его воспроизводить. Кроме того, полученное в результате данного подхода основное уравнение не имеет вполне законченного очень простого вида.

В настоящей работе мы дадим полный и довольно простой вывод основного уравнения эллипсометрии с выделенным j -м слоем, определяющего поляризационные углы Т и А для N -слойной системы через рекуррентные соотношения. При этом будем использовать простые исходные выражения, не прибегая к аналитическому выражению для полной матрицы N -слойной системы.

Основное уравнение эллипсометрии для отражающей системы "подложка— N однородных слоев" (см. рисунок) в его наиболее общей форме выражается через элементы полной матрицы Абелеса M _p ( _s ) (0, z ₀), представленной в виде произведения матриц отдельных слоев [6]:

M p ( , ) (0, z 0 ) = M™ ) ( d j ) М <Д > ) ( d 2 )... M p^N >( d N ). (16)

Для матриц удобно использовать новые обозначения

M p ( ₄ ) (0, z 0 ) - M p ( ₄ ) [1, N ],

M ⁽ p)_s ) ( d_k ) - M p ( ₄ ) [ k ],   ( k = 1,2,

с учетом которых (j6) запишется:

..., N ),

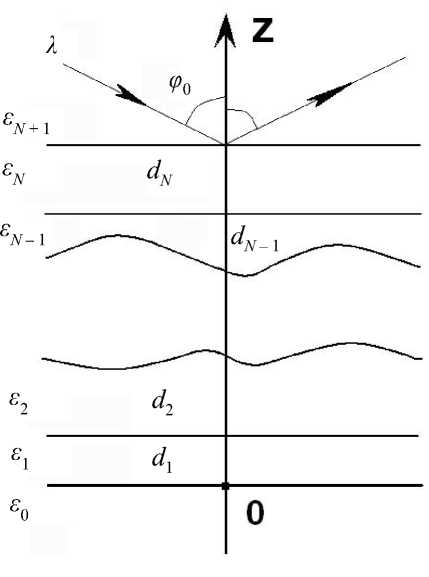
Схематическое изображение N -слойной отражающей системы

где

M p ( , ) [ k ]

∼

a

h p ( s ) ^{[ k ]} a

a h p ( s ) [ k ] a k ⁺⁾

,

h p [ k ] = —, h s [ k ] = g k , ^E k

-En+1 sin2Фo, (k = 0,1,...,N,N +1), a^ = exp(-2i8k) ± 1,

5 _k = ^П d k g k ,   ( k = 1,2,..., N ).

A

В формулах (20) e0 и en+1 — диэлектрические проницаемости подложки и внешней среды, Ek и dk (k = 1, 2, ... , N) — диэлектрическая проницаемость и толщина k-го однородного слоя (см. рисунок). Будем также иметь в виду, что комплексные амплитудные коэффициенты отражения Френеля для p- и s-волн на границе k-й и (k + 1)-й сред определяются формулами r [k + 1 k] = hp(s)[k + 1] - hp(s)[k]

p ⁽ s )        ’       h p ( s ) [ k + 1] + h p ( s ) [ k ],        (21)

(k = 0,1,..., N), а для матриц выполняются очевидные соотношения:

M p ( s ) [ k , N ] =

= M p ( s ) [ k ] M p ( s ) [ k + 1]... M p ( s ) [ N ], k <  N ;

M p ( s ) [ k , N ] =                                    ⁽²²⁾

= M p ( s ) [ k ] M p ( s ) [ k + 1, N ],    k <  N ;

M p ( s ) [ N , N ] = M p ( s ) [ N ].

Элементы матрицы M _{p ( s} ) [ k , N ] будем обозначать через m_{p ( s} а [ k , N ] ( а , в = 1,2). В новых обозначениях исходное основное уравнение эллипсометрии для N -слойной системы имеет следующий вид [6]:

R              K ^{( + )}

tg Т exp( i А ) = -p ,     R p ( s ) ~ -Np l s l ,      (23)

R s                 K N , p ( s )

где

K^ p ( s ) = G p ± )) [1, N + 1] - h p ( s ) [0] Q p ± )) [1, N + 1], (24)

G p ± )) [1, N + 1] =

= m p ( s )₂1 [1, N ] ± h p ( s ) [ N + 1] m p ( s )₂₂ [1, N ],         (25)

Q p ± )) [1, N + 1] =

= m p ( s )_П [1, N ] ± h p ( s ) [ N + 1] m p ( s )1₂ [1, N ].          (26)

В формуле (23) для R_{p ( s} ) опущен отрицательный экспоненциальный множитель, общий для R_p и R_s , и, следовательно, не проявляющийся в основном уравнении.

Характер нижеследующих преобразований таков, что выражение (24) для K N_p ( _s ) целесообразно представить в виде

K'^ p ( s ) = A p ( s ) [0]( G p ± )) [1, N + 1] +

+ h p ( s ) [0] Q p ± )) [1, N + 1]) +

+ B p ( s ) [0] ( G p ± )) [1, N + 1] - h p ( s ) [0] Q p ± >) [1, N + 1]). (27)

Коэффициенты A_{p ( s} ) [0] и B_{p ( s} ) [0] в (27), очевидно, должны иметь такие значения, чтобы сохранялось выражение (24):

A p ( s ) [0] = 0,      B p ( s ) [0] = 1.                (28)

Преобразуем формулы (25) и (26). Для этого представим полную матрицу в виде (см. вторую формулу из (22) при к = 1)

M p ( , ) [1, N ] = M p ( , ) [1] M p ( , ) [2, N ].          (29)

Учитывая формулы (19) и (29), найдем:

G p ± Р[1, N + 1] =

= a + G p ± )) [2, N + 1] + h p ( s ) [1] a ( ^{- )} Q p ± )) [2, N + 1], (30)

QA S ) [1, N + 1] =

= a ( ^{+ )} Q p ± )) [2, N + 1] + -L- a ( ^{- )} G < ± >> [2, N + 1], (31) h p ( s ) ^[1]

где величины Gp±S)[2, N +1] и Q\±S)[2, N +1] определяются формулами (25) и (26), в которых надо сделать переход mp(sа [1, N] ^ mp(sw [2, N],   (а, в = 1,2).   (32)

Теперь подставим (30) и (31) в выражение (27) для K N¹*_p ( _s ) и сделаем элементарные преобразования, в результате которых появятся коэффициенты отражения Френеля и общий множитель

(hp (s )[1] + hp (s )[0]) hp (s)Ш       ’ который можно опустить как не имеющий значения ни для Rp(s), ни для основного уравнения. В итоге величина KN±)p(s) запишется:

K N ± p ( s ) ~ A p ( s ) [1]( GA )) [2, N + 1] +

+ h p ( s ) [1] QA s ) [2, N + 1]) +

+ B p ( s ) [1] ( GA )) [2, N + 1] - h p ( s ) [1] Q p ± )) [2, N + 1]). (33)

В формуле (33) появились новые величины A_p ( _s ) [1] и B_p ( _s ) [1], которые определяются через A p ( s ) [0] и B p ( s ) [0] (см. (28)):

a p ( s ) [1] =

= ( A p ( s ) [0] + r p ( s ) [1,0] B p ( s ) [0]) exp( - 2 / Д),         (34)

B p ( s ) [1] = r p ( s ) [1,0] A p ( s ) [0] + B p ( s ) [0].                (35)

Как видим, выражение (33) имеет точно такую же структуру, как и исходное выражение (27) для K N¹*_p ( _s ) . Принимая во внимание (34) и (35), можно утверждать, что это первый шаг в направлении движения от подложки к верхней границе системы.

Если затем воспользуемся представлением

M p ( s ) [2, N ] = M p ( s ) [2] M p ( s ) [3, N ]         (36)

и выражением (33) для K N ^t) _{p ( s} ) , то точно такие же преобразования позволят сделать следующий шаг в определении величины K N’_p ( _s ) . Используя метод математической индукции, легко показать, что на к -м шаге величина K N ± ) _{p ( s} ) определится выражением

K N ± p ( s ) ~ A p ( s ) [ к ] x

x ( G p ± )) [ к + 1, N + 1] + h p ( s ) [ к ] Q )) [ к + 1, N + 1] ) +

+ B p ( s ) [ к ] x

x ( G p ± )) [ к + 1, N + 1] - h p ( s ) [ к ] Q p ± )) [ к + 1, N + 1] ) , (37) в котором основные величины определятся формулами, аналогичными (25), (26) и (34), (35):

G p ± )) [ к + 1, N + 1] =

= m p ( s )21 [ к + 1, N ] ± h p ( s ) [ N + 1] m p ₍ , ) ₂₂[ к + 1, N ], (38)

QA )) [ к + 1, N + 1] =

= m p ( s )11 [ к + 1, N ] ± h p ( s ) [ N + 1] m p ₍ , ) ₁₂ [ к + 1, N ],   (39)

A p ( s ) [ ^к ] =

= (Ap(s)[к -1] + rp(s)[к, к -1] Bp(s)[к - 1])x x exp(-2 iЗk),                                  (40)

B p ( s ) [ к ] = r p ( s ) [ к , к - 1] A p ( s ) [ к - 1] + B p ( s ) [ к - 1], (41) где 1 <  к <  N - 1.

Используя (37), определим K^ N^_p ( _s ) на ( N- 1)-м шаге:

KN±p(s) ~ Ap(s)[N-1]x x (Gp±s) [N, N +1] + hp(s) [N -1] Qp±s) [N, N +1]) +

+ B p ( s ) [ N - 1] x

x ( G p ± )) [ N , N + 1] - h p ( s ) [ N - 1] Q p ± )) [ N , N + 1] ) . (42)

Здесь A_{p ( s} ) [ N - 1] и B_{p ( s} ) [ N - 1] очевидно определяются соотношениями (40) и (41), а величины G p ± )) [ N , N + 1] и Q p ± )) [ N , N + 1] - формулами (38) и (39), в которых при к = N - 1

m p ( s) ав [ N , N ] = m p ( ,) а _Р [ N ],   ( а , в = 1,2).    (43)

Учитывая (43), а также формулу (19), определяющую (при k = N) матрицу N -го однородного слоя, т. е. элементы m_{p ( s w} [ N ], найдем

G Р ± )) [ N , N + 1] =

= h p ( - ) [ N ] a N " ± h p ( - ) [ N + 1] a N ,              (44)

Q p ± )) [ N , N + 1] = a N ) ± h p ( ^{- ) [} N + ^1] a N .      (45)

h p ( - ) ^{[ N ]}

Подставляя (44) и (45) в (42) и привлекая формулы (20) и (21), получим окончательные выражения для K Np ( - ) ^и K N - ) p ( - ) ^:

K^ p ( - ) ~ A p ( - ) [ N ] + Г р ( - ) [ N + 1, N ] B p ( - ) [ N ],    (46)

K -^ ( - ) ~

~ ( - 1) ( r p ( - ) [ N + 1, N ] A p ( - ) [ N ] + B p ( - ) [ N ] ) ,      (47)

где r_p ( _- ) [ N + 1, N ] — коэффициенты отражения Френеля на границе внешней среды и верхнего слоя (см. рисунок), а величины A_{p ( -} ) [ N ] и B_{p ( -} ) [ N ] удовлетворяют соотношениям (40) и (41), распространенным на случай k = N . Множитель (-1) из (47) переходит в выражения для R_p и R_- (после подстановки (46) и (47) в (23)), но в основном уравнении он сокращается, поэтому окончательный вид основного уравнения эллипсометрии будет следующим:

tg Т exp( i А ) =

Ap [ N ] + rp [ N +1, N ] Bp [ N ] x rp [ N +1, N ] Ap [ N ] + Bp [ N ]X x r- [ N +1, N ] A- [ N ] + B- [ N ] A- [ N ] + r- [ N +1, N ] B- [ N ]"   (48)

определенные формулами (28). Уравнение (48) совместно с (49) и (50) позволяет легко рассчитать поляризационные углы Т и А для любой многослойной системы, что особенно важно для математических программ, связанных с расчетом Т и А .

При N = 0 уравнение (48) в соответствии с (28) переходит в уравнение для чистой подложки r [1,0]

tg Т exp( i А ) =        .            (51)

r - [1,0]

Перейдем теперь к выводу основного уравнения эллипсометрии с выделенным произвольным j -м слоем

1 < j < N, точнее, выделим в основном уравнении величину exp(-2iSj), отвечающую этому слою. Основой для такой процедуры являются рекуррентные соотношения (49) и (50). Величины Ap(-)[m] и Bp(-)[m], в которых m = 1, 2, ... , j-1, определим данными соотношениями, не прибегая ни к какой модификации этих величин. Для величин Ap(-)[j] и Bp(-)[j], определенных теми же соотношениями, сделаем элементарные преобразования:

Ap (-)[ j ] = A p (-)[ j ]exp(-2 iSj),(52)

A p ( - ) [ j ] =

= Ap(-) [ j -1] + rp(-) [ j, j -1] Bp(-) [ j -1],(53)

Bp (-)[ j ] - B0 p (-)[ j ],(54)

B 0 p (-)[ j ] =

= r p ( - ) [ j , j - 1] A p ( - ) [ j - 1] + B p ( - ) [ j - 1].

Основное уравнение (48) базируется на использовании рекуррентных соотношений, совпадающих с (40) и (41), но имеющих более широкую область применения, поэтому перепишем их в законченной форме:

a p ( - ) ^{[ m ]} =

= ( Ap (-)[ m -1] + rp (-)[ m, m -1] Bp (-)[ m -1])x x exp(-2 ism x                                (49)

B p ( - ) ^[ m ^] =

= r p ( - ) ^{[ m} , ^{m - 1]} A p ( - ) ^{[ m - 1] +} B p ( - ) ^{[ m - 1]} ,      (50)

Величины A_{p ( -} ) [ m ] и B_{p ( -} ) [ m ], в которых m = j , j +1, „., N , определим теперь в другом более удобном виде, используя (49), (50) и (52-55) и выделяя в явной форме экспоненту j -го слоя — exp( - 2 i S j ). В результате для данных величин придем к выражениям с коэффициентами, определяемыми рекуррентными соотношениями другого вида. Чтобы получить эти выражения и соответствующие рекуррентные соотношения, запишем величины A_p ( _- ) [ m ] и B_p ( _- ) [ m ] в наиболее общей форме:

^A p ( - ) ^[ m ^] = / p ( - )11 ^[ m ^{] e} xp ^{( - 2 i S} j ) ^{+ f} p ( - )12 ^{[ m ]} ,     ⁽⁵⁶⁾

где m = 1,2,..., N - 1, N .

Начальными значениями для рекуррентных соотношений являются величины A_{p ( -} ) [0] и B_{p ( -} ) [0],

^Bp ( - ) ^{[ m ]} =

= ^f p ( - )21 ^[ m ^{] e} xp ^{( - 2 i S} j ) ^{+ f} p ( - )22 ^[ m 1» где ( m = j , j + 1,..., N ).

Коэффициенты f_{p ( s ) ар} [ m ] ( а , в = 1,2) удовлетворяют рекуррентным соотношениям. Чтобы найти эти соотношения, рассмотрим сначала выражения (56) и (57) для случая m = j :

A p ( , ) [ j ] = f p ( , )ii [ j ] exp( - 2 i S j ) + f p ( , )12 [ j ],       (58)

B p ( , ) [ j ] = f p ( , )2i [ j ] exp( - 2 i S j ) + f p ( , ₎₂₂[ j ].       (59)

Сравнивая (58) и (59) с (52) и (54), находим fp (, )ii[ j ] = A, p (,)[ j ],

f p ( , )21 [ j ] = 0,

fp (, )12[ j ] = 0, fp (, )22[ j ] = B0 p (,)[ j ],

где A_{p ( s} ) [ j ] и B _{0 p ( s} ) [ j ] определяются выражениями (53) и (55).

Затем рассмотрим формулы (56) и (57) для случая m = j + 1. Чтобы определить коэффициенты fp(s)ар [j +1] из этих формул, воспользуемся рекуррентными соотношениями (49) и (50), записанными для m = j + 1. Подставив в них (58) и (59) для Ap (s)[ j ] и Bp (s)[ j ], найдем выражения для Ap(s)[j +1] и Bp(s)[j +1]. Представив данные выражения в форме (56) и (57) (при m = j + 1), найдем для коэффициентов fp(s)ар [j +1] следующие вы ражения:

f p ( s )!> [ j + 1] =

= (fp(s)11[j] + rp(s)[j + 1, j] fp(s)21[j]) X x exp(-2 isj+1X fp (s )12[ j +1] =

= (fp(s)12[ j] + rp(s)[ j + 1 j] fp(s)22[ j]) X x exp(-2 isj+1),

fp(s)21[ j + 1] = rp(s) [ j + 1 j] fp(s)11 [ j] + fp(s)21 [ j] , fp (s )22[j + 1]   rp (s)[ j + 1 j] fp(s)12 [ j] + fp(s)22 [ j] .

Аналогичным образом получаются коэффициенты f_p ( _s ) _а р [ j + 2] и все следующие коэффициенты вплоть до f_p ( _s ) _а р [ N ]. Учитывая характер данной последовательности и используя метод математической индукции, легко показать, что коэффициенты f_p ( _s ) _а р [ m ] удовлетворяют следующим рекуррентным соотношениям:

^f p ( s )11 ^[ m ^] =

= (fp(s)11[m — 1] + rp(s) [m, m — 1] fp(s)21 [m — 1]) X x exp(-2 iSm), fp (s )12[ m ] =

= (fp(s)12[m — 1] + rp(s)[m, m — 1] fp(s)22[m — 1]) X x exp(-2 iSm ), fp (s )21[ m ] =

= r p ( s ) ^[ m , m — ^{1] f} p ( s )11 ^[ m — ^{1] + f} p ( s )21 ^[ m — ^1] ,

^f p ( s )22 ^[ m ^] =

= rp(s) [m, m — 1] fp(s)12[m — 1] + fp(s)22 [m — 1], где m удовлетворяет условию m = j+1, j+2, _ , N.

Полученные рекуррентные соотношения (62) предполагают предварительное использование рекуррентных соотношений (49) и (50) (для m = 1, 2, „., j- 1) и формул (60), определяющих начальные коэффициенты f_p ( _s ) _ар [ j ] для соотношений (62).

Теперь можем определить основное уравнение эллипсометрии для N -слойной отражающей системы с выделенным j -м слоем. Для этого представим входящие в основное уравнение (48) величины A_{p ( s} ) [ N ] и B_{p ( s} ) [ N ] в виде выражений (56) и (57), положив в последних m = N :

A p ( s ) [ N ] = f p ( s )11 [ N ] exp( - 2 i S j ) + f_p ( , )1 ₂[ N ],   (63)

B p ( s ) [ N ] f p ( s )21 [ N ]exp( - 2 i S j ) + f p ( s )22 [ N ].   (64)

Коэффициенты f_p ( _s ) _а р [ N ], входящие в формулы (63) и (64), определяются с помощью рекуррентных соотношений (62).

Подставив (63) и (64) в уравнение (48), после несложных преобразований придем к основному уравнению эллипсометрии для N -слойной системы с выделенным j -м слоем:

tg Т exp( i А ) =

X1 p[N]exp(-2 iSj) + Z1 p[N] x X2 p [ N ]exp(-2 iSj) + Z 2 p [ N ]X x X2s[N]exp(-2 iSj) + Z2s[N]

X X1 s[N]exp(-2iSj) + Z1 s[N], где

X 1 p ( s ) [ N ] =

= fp (s )11 [ N ] + rp (s) [ N +1, N ] fp (s )21 [ N ],(66)

Z 1 p ( s ) [ N ] =

= fp (s )12[ N ] + rp (s)[ N +1, N ] fp (s )22[ N ],(67)

X 2 p ( s ) [ N ] =

= fp(s)11 [N] rp(s) [N +1, N] + fp(s)21 [N],(68)

^Z 2 p ( s ) ^{[ N ] =}

= f p ( s )12 [ N ] r p ( s ) [ N + 1, N ] + f p ( s )22 [ N ].           (69)

Если выделенным является верхний слой j = N , то, согласно (60) и (66–69):

^X 1 p ( s ) ^{[ N ] = A} 0 p ( s ) ^{[ N ],}

Z 1 p ( s ) [ N ] = r p ( s ) [ N + 1, N ] B 0 p ( s ) [ N ],            (70)

X 2 p ( s ) [ N ] = r p ( s ) [ N + 1, N ] A 0 p ( s ) [ N ],

Z2p(s)[N]=B0p(s)[N], и уравнение (65) запишется:

tg Ψ exp( i ∆ ) =

₌ A 0 p [ N ]exp( - 2 i δ N ) + r p [ N + 1, N ] B 0 p [ N ] _× r p [ N + 1, N ] A 0 p [ N ]exp( - 2 i δ N ) + B 0 p [ N ]

_× r s [ N + 1, N ] A 0 s [ N ]exp( - 2 i δ N ) + B 0 s [ N ]      ₍₇₁₎

A 0 s [ N ]exp( - 2 i δ N ) + r s [ N + 1, N ] B 0 s [ N ] ^.

Уравнение (71), очевидно, можно получить также, используя (48), (52), (54), полагая в последних j = N .

• 3.    МЕТОД ХОЛМСА ДЛЯ N -СЛОЙНОЙ СИСТЕМЫ. ОСНОВНЫЕ ФОРМУЛЫ

Способ записи основного уравнения эллипсометрии для N -слойной системы, выделяющий в явной форме экспоненту отдельного j -го слоя, позволяет обобщить на случай многослойных поглощающих сред метод Холмса [7]. Здесь мы ограничимся только приведением основных формул.

Преобразуем уравнение (65), сведя его к квадратному относительно exp(-2 iδj ) уравнению. Это уравнение с учетом новых обозначений x ≡ exp(-2 iδj ),    ρ= tgΨexp(i∆)(72)

запишется aNx2 +bNx+cN=0,(73)

где aN=ρX1s[N]X2p[N]-X1p[N]X2s[N],(74)

b_N =

= ρ ( X 1 s [ N ] Z 2 p [ N ] + X 2 p [ N ] Z 1 s [ N ]) -

-(X1p[N]Z2s[N]+ X2s[N]Z1p[N]),(75)

cN=ρZ1s[N]Z2p[N]-Z1p[N]Z2s[N].(76)

Из (73) находим выражение для экспоненты j -го слоя:

-b±b2 -4ac x12≡(exp(-2iδj))12=NNNN.(77)

^{,                      ,}                2 a N

На выборе знака перед корнем в данном выражении остановимся ниже. А пока представим выражение (77) в удобном для дальнейшего виде:

exp( - 2 i δ j ) = F N ,               (78)

где F_N определяется правой частью формулы (77) с правильно выбранным знаком перед корнем.

С другой стороны, экспонента j -го слоя (через величину δ _j в показателе экспоненты) зависит от оптических постоянных и толщины j -го слоя, а также от показателя преломления внешней среды (см. (20) при k = j ). Используя это первичное представление экспоненты, запишем (78) в следующем виде:

4 π exp( - id_jg_j ) = F_N .          (79)

λ

Затем преобразуем уравнение (79), применяя процедуру, аналогичную использованной в работе [1]. Выразим комплексные в общем случае величины ε _j и g_j через оптические постоянные ( n_j , k_j ) j -го слоя:

εj=(nj-ikj)2=εj1-iεj2,

εj1=n2j-k2j,εj2=2njkj, gj=εj-εN+1sin2ϕ0=gj1-igj2,

2gj1gj2=εj2, g=× j1

× ( ε _{j 1} - ε _{N + 1}sin ² ϕ ₀) ² + ε ² _{j 2} + ( ε _{j 1} - ε _{N + 1}sin ² ϕ ₀). ⁽⁸²⁾

В (81) интерес представляет вторая формула, связывающая величины g_{j 1} и g_{j 2} . При ε _{j 2} = 0 , что имеет место при k_j = 0, g_{j 2} = 0 .

Используя (80–82), приведем уравнение (79) к виду exp(-i ξj) exp(-ηj) = FN,          (83)

где

4 π d_j ξ j ⁼ _λ ^g j 1 ^,

4 π d_j ^η j ⁼ _λ ^g j 2 ^,

или

^ j

2ndj

D0 j ,

n

^{2 n d} j g j 2 _ ^{n d} j ^£ j 2 _ ,  ^£ j 2

2 j 2 ^, 0 j ^g j 1       0 j ^g j 1           ^g j 1

большую толщину. Как увидим ниже, понятие относительно большой толщины здесь точно такое же, как и для прозрачных слоев, описанных в работе [3].

Подставив в уравнение (87) выражение (85) для ^ _j , получим формулу для толщины пленки:

^D 0 j =

X

. 2 g j 1

Представим также комплексную правую часть уравнения (83) в экспоненциальном виде:

exP ⁽ - i ^ j ) eM-B j ) = ^F 0N exP ⁽ - i P n ) ,       ⁽⁸⁶⁾

где F_{0 N} — модуль, а ( - P _N ) — аргумент комплексной величины F_N , принадлежащий интервалу (0, - 2 п ). Комплексное уравнение (86), очевидно, разделяется на два действительных

^j_ Pn + 2п m,   (m _ 0,1,2,...),(87)

d j_\ eL D 0j + mD 0         ( m _ 0,1,2,...). (91)

I 2 n j ^J

Запишем эту формулу в виде dj_ d0j+ mD0j,(92)

где d0j_\eN D0j.(93)

I 2 n j

Поскольку PN изменяется в пределах интервала (0,2п), то величина d0j удовлетворяет условию exp!-'/ ) = F0 N

0 <  d 0j < D 0 j .

Из уравнения (88) непосредственно следует условие на модуль величины F_N :

F N <  1,                        (89)

в котором знак равенства отвечает случаю прозрачного j -го слоя, для которого

^:' _ 0, n j _ 0.                   (90)

Условием (89) определяется выбор знака перед корнем выражения (77), однако надо иметь в виду, что данное условие строго выполняется, если точно известны все параметры N -слойной системы.

В данной работе метод Холмса не интересует нас в плане непосредственного определения параметров многослойной системы. В то же время приведенные в этом разделе уравнения (87) и (88) представляют большой интерес, но уже несколько другого характера в связи с решением математически некорректной обратной задачи эллипсометрии для многослойных систем с поглощающими слоями, особенно, если один из поглощающих слоев имеет относительно большую толщину.

• 4.    ОБЩИЕ СВОЙСТВА РЕШЕНИЯ ОСНОВНОГО УРАВНЕНИЯ ЭЛЛИПСОМЕТРИИ ДЛЯ МНОГОСЛОЙНОЙ СИСТЕМЫ

С ПОГЛОЩАЮЩИМ СЛОЕМ ОТНОСИТЕЛЬНО БОЛЬШОЙ ТОЛЩИНЫ. МЕТОД РЕШЕНИЯ ОБРАТНОЙ ЗАДАЧИ

Рассмотрим N -слойную систему, в которой j -й слой обладает поглощением и имеет относительно

В случае прозрачной пленки величина D _{0 j} , определяемая формулой (85), играет роль периода по толщине d_j для поляризационных углов Т и А . В случае же поглощающей пленки углы Т и А уже не обладают периодичностью по толщине, однако и в том, и в другом случае периодичностью по толщине d_j с периодом D _{0 j} обладает величина P _N , зависящая от толщины пленки через углы Т и А . С учетом (91-93)

• d, - mDn,d

Pn (d) _ 2n j     0j _ 2n    _ Pn (d0j)(95)

D0j и, следовательно,

Pn (d0j+ mD0j) _ Pn (d0j) .(96)

Таким образом, независимо от характера пленки (прозрачная или поглощающая) полная толщина d _j представляется формулой (92), в которой выделяется целое число (начиная от 0) периодов D _{0 j} и остаток d _{0 j} , меньший величины периода (см. (94)). Период D _{0 j} , а следовательно, и остаток d _{0 j} зависят от угла падения ф ₀.

Относительно толстой мы называем пленку, толщина которой удовлетворяет условию dj> D0j,                     (97)

т. е. dj содержит в себе несколько (как минимум, один) периодов. При исследовании многослойных систем с такими пленками определение числа периодов, т. е. определение целого числа m из формулы (92) является важнейшей задачей.

В данной работе нас интересуют относительно толстые поглощающие пленки. В принципе, для определения числа периодов, содержащихся в полной толщине d_j поглощающей пленки, можно было бы использовать уравнение (88). Это уравнение после несложных преобразований, связанных с использованием формул (85) и (87), приобретает вид

г exp -(3N + 2пт)^Т = F 2 gn

0 N ^.

Уравнение (98) в общем случае многослойной поглощающей среды, очевидно, не позволяет определить все неизвестные параметры, включая целое число m , а это означает, что необходимо использовать систему уравнений (98), отвечающих некоторому набору углов падения ф 0 . В этом случае предполагается, что толщина d _j определится из формул (92) и (93).

Однако такой подход, представляющий собой обобщение метода Холмса на многослойные среды, по определенным причинам не является удовлетворительным. Обратная задача эллипсометрии для многослойных сред с поглощающими относительно толстыми слоями обладает выраженной математической некорректностью. Особенно это проявляется при исследовании нарушенных слоев на поглощающих материалах, например на полупроводниках. В этом случае приходится учитывать также естественную окисную пленку на поверхности материала. Очень малая толщина окисной пленки, большая протяженность и оптическая неоднородность (по толщине) нарушенного слоя, а также слабое отличие оптических постоянных нарушенного слоя от объемных значений превращают поверхность поглощающих материалов в сложный для исследования объект. Обратную задачу эллипсометрии для таких систем приходится решать с учетом большого числа неизвестных параметров, а это выдвигает жесткие требования к методам решения обратной задачи.

Для решения обратной задачи, как и в работе [3], посвященной исследованию многослойных систем с относительно толстыми прозрачными пленками, будем использовать измерения поляризационных углов Т и А на многих углах падения, рассматривая в качестве целевой функции соответствующую среднеквадратичную невязку. Набор углов падения должен быть таким, чтобы на нем проявлялись характерные особенности в поведении поляризационных углов, связанные с углами полной поляризации.

Анализ ситуации, связанной с зависимостью от угла падения величин d _{0 j} , и D _{0 j} , и целого числа m , определяющих полную толщину d _j поглощающего слоя (см. (92)), носит точно такой же характер, как и в работе [3]. Данный анализ показывает, что при решении обратной задачи определению подлежат величины d _{0 j} и m , отвечающие только какому-то одному углу падения из используемого набора, например минимальному углу. Это означает, что в основное уравнение эллипсометрии при расчете углов Т и А для всего набора углов падения подставляется выражение (92), отвечающее выбранному углу падения.

Для решения обратной задачи в случае многослойной поглощающей системы, как и в работе [3], нами использован комплексный метод Бокса [8]. Этот метод, если использовать процедуру пошаговой минимизации, подробно описанную в той же работе [3], дает неплохие результаты при поиске неизвестных параметров системы, число которых не превышает 7–8. При определении большего числа параметров математическая программа, разработанная на основе прямого использования метода Бокса, дает уже неудовлетворительные результаты. Как раз такая ситуация и возникает при исследовании нарушенных слоев на поглощающих материалах, когда приходится учитывать еще и прозрачный слой естественного окисла. В связи с этим мы существенно модифицировали метод Бокса. Использование метода Бокса приобретает гораздо более сложный характер. Это относится и к набору точек комплекса, и к выбору начальной точки, но и в том, и в другом случае соответствующие процедуры по-прежнему основаны на статистическом подходе. Особое значение при исследовании сложной поглощающей системы, один из слоев которой имеет произвольную толщину (может быть относительно толстым), является разработка новых критериев выбора оптимального решения обратной задачи. Для данного сложного случая критерий выбора, использованный в работе [3], уже не является достаточным. Поэтому разработаны новые критерии выбора оптимальной точки, основанные на использовании формул метода Холмса, обобщенного на многослойные системы. Именно поэтому в настоящей работе мы подробно остановились на данном обобщении метода Холмса.

На всех этих вопросах, касающихся решения обратной задачи эллипсометрии для сложных поглощающих систем, мы подробно остановимся в отдельной работе, посвященной исследованию конкретных объектов. При этом важные выводы будут сделаны и на основе численного эксперимента.