О параллельном алгоритме перечисления триангуляций многоугольника на плоскости

DOI:

1.    Задача построения всех триангуляций многоугольника на плоскости © Попов В.В., 2016

Вопрос о построении триангуляций множества точек на плоскости рассматривался многими авторами (см., например, [5–8]). В работе [1] предложен алгоритм построения всех триангуляций конечного множества на плоскости. Соответствующий алгоритм для трехмерного пространства описан в [2]. В работе [8] изучается граф, вершинами которого являются триангуляции конечного набора точек Р С R ² , причем две триангуляции связаны ребром в том и только том случае, когда найдутся четыре точки множества Р , являющиеся вершинами выпуклого четырехугольника, такие, что в одной триангуляции этот четырехугольник разбит на два треугольника одной диагональю, а в другой триангуляции — другой диагональю (все остальные треугольники в этих триангуляциях одинаковы). Переход от одной триангуляции к другой в этом случае называется перестроением (или флипом, flipping). В работе [3] строится другое дерево, вершинами которого являются триангуляции (а также другие прямолинейные геометрические графы) с вершинами в заданном конечном подмножестве плоскости.

В данной статье рассматривается следующая задача.

На плоскости дан замкнутый многоугольник F и конечное множество точек Р = = { р 1 ,р ₂ , ... ,P n } , включающее все вершины этого многоугольника. Необходимо перечислить все триангуляции многоугольника F относительно набора точек Р .

Ниже предлагается параллельный алгоритм решения этой задачи. Часть результатов объявлена в [4].

Под многоугольником понимается область плоскости, ограниченная замкнутой неса-мопересекающейся ломаной. Триангуляция Т многоугольника F относительно набора точек Р — это набор треугольников S 1 , S 2 , ... , S _m , удовлетворяющий следующим условиям:

• (1)    Каждая точка р ^ Е Р является вершиной хотя бы одного из треугольников S j .

• (2)    Вершины любого треугольника S j лежат во множестве Р .

• (3)    Если г = з , то треугольники S t и S j или не пересекаются, или имеют только общую вершину, или только общее ребро.

• (4)    Объединение треугольников S 1 , S 2 , ... , S _m совпадает с многоугольником F .

Через Тr(F,Р ) будем обозначать множество всех триангуляций набора точек Р , удовлетворяющих условиям (1)–(4). Таким образом, необходимо перечислить все триангуляции Т Е Тr(F,Р ) . При построении параллельного алгоритма решения этой задачи используется понятие перегородки.

Пусть I — прямая, пересекающая многоугольник F и не содержащая точек множества Р . Назовем перегородкой, определяемой тройкой F , Р , / , набор треугольников П , который удовлетворяет таким условиям:

• (а)    Вершины любого треугольника S Е П лежат во множестве Р.

• (b)    Различные треугольники S, S‘ Е П или не пересекаются, или пересекаются по общей вершине или по общему ребру.

• (c)    Объединение всех треугольников S Е П содержит множество F П I и само содержится в F.

2.    Последовательный алгоритм построения триангуляций многоугольника F относительно набора точек Р

На рисунке 1 слева изображен многоугольник F , множество Р и прямая / , в центре — одна из триангуляций Т Е Тr(F,Р ) , а справа — соответствующая этой триангуляции перегородка П (треугольники, составляющие перегородку, изображены серым цветом).

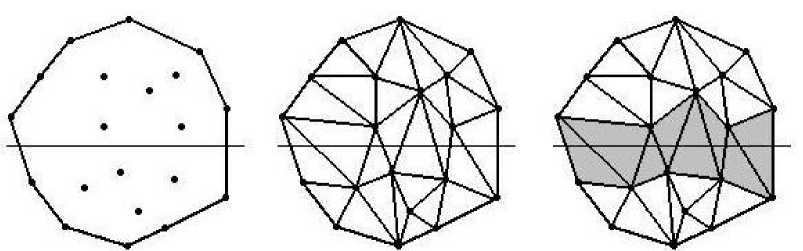
Рис. 1. Многоугольник F , множество Р и прямая I ( слева ), одна из триангуляций ( в центре ) и соответствующая этой триангуляции перегородка Π ( справа )

Как уже указывалось выше, в [1] описан алгоритм перечисления всех триангуляций конечного множества на плоскости. Опишем более компактный алгоритм, который можно применять не только к многоугольникам, но и к объединениям конечного числа многоугольников. Последнее важно для построения параллельного алгоритма.

На каждом шаге алгоритма будет определен набор треугольников

S i ,S 2 ,...,S _k - i ,                                     (1)

который можно достроить до некоторой триангуляции многоугольника F относительно набора точек Р . Через a _i , b i и c _i будем обозначать номера точек множества Р , являющихся вершинами треугольника S _i , i = 1, 2,..., к — 1 .

Будем использовать также следующие обозначения:

(i,j ) — ребро (прямолинейный отрезок), соединяющее вершины множества Р с номерами i и j . Ребра считаем неориентированными, поэтому ребро (i, j ) совпадает с ребром (j, i) ;

к — номер строящегося треугольника;

т — число треугольников в любой триангуляции множества Р l. Это число определяется после того, как построена первая триангуляция;

ktr — число всех триангуляций множества Р относительно многоугольника F , то есть ktr = | Tr(F,Р ) | . В начале работы алгоритма ktr = 0 .

Функция Df (i, j ) позволяет узнать — является ли (i, j ) стороной (граничным отрезком) многоугольника F или нет. В первом случае Df (i,j) равно 1 , а во втором 0 . Если (i, j ) — некоторое ребро, то будем называть его кратностью число треугольников в последовательности (1), для которых это ребро является стороной. Если кратность ребра (i, j) равна 1 и Df(i,j ) = 0 , то будем называть это ребро граничным. Если граничное ребро появилось при добавлении треугольника S _k , то оно будет запоминаться как ребро (u _k , r _k ) . Если же при добавлении треугольника S _k граничное ребро не появилось, то переменной u _k присваивается значение 0 . Если е = (u _k ,r _k ) — граничное ребро (возникшее при добавлении треугольника S _k ) и в дальнейшем к последовательности (1) был добавлен треугольник S / , I > к , для которого ребро е является стороной, то е перестанет быть граничным. Этот факт фиксируется путем присвоения переменной r _k значения / . Для граничного ребра r _k = 0 .

На каждом шаге работы алгоритма будет определено базовое ребро (i 1 , i ₂ ) , к которому будет подыскиваться число j такое, что треугольник с номерами вершин i 1 , i ₂ и j можно добавить к последовательности (1) в качестве S _k . Это будет осуществляться с помощью функции f (i 1 ,i ₂ ,i ₃ ) , которая и возвращает нужное j c дополнительным условием i ₃ < j <  N . Если такого j не найдено, то возвращается значение 0 .

Функция у(к) находит наименьшее целое число j , для которого 1 <  j < к и (u j ,V j ) является граничным ребром для последовательности (1). Если такого j не найдено, то у (к) возвращает значение 0 .

Алгоритм построения списка триангуляций

ДАНО:       многоугольник F на плоскости (не обязательно выпуклый);

множество Р из N точек плоскости, лежащее в F и содержащее все вершины многоугольника F ;

базовое ребро (i 1 ,i ₂ ) , являющееся стороной многоугольника F .

ПОЛУЧИТЬ: список всех триангуляций многоугольника F относительно множества Р .

• 1)    Полагаем к = 1 , т = 0 и ktr = 0 . При всех i,j = 1, 2,..., N кратность ребра (i, j) полагаем равной 0 . Полагаем также а 1 = i 1 и b 1 = i ₂ .

• 2)    Полагаем с _к = 0 .

• 3)    Полагаем j = / (а _к ,Ь _к ,с _к ) . Если j <  0 , то идем на пункт 8.

• 4)    Полагаем с _к = j . Кратности ребер треугольника S _k (номера вершин которого а _к , b _k и с _к ) увеличиваем на 1 .

• 5)    Если т >  0 и к >  т , то идем на пункт 10.

• 6)    Полагаем и _к = 0 .

• 7)    a) Если D/(а _к ,с _к ) = 0 и кратность ребра (а _к ,с _к ) равна 1 , то полагаем а _к+1 = а _к и Ь _к+1 = с _к . Если, дополнительно, D/(Ь _к ,с _к ) = 0 и кратность ребра (Ь _к ,с _к ) равна 1 , то полагаем и _к = Ь _к , ^ _к = с _к и г _к = 0 .

Увеличиваем к на 1 и идем к пункту 2.

• b)    Если D/(Ь _к ,с _к ) = 0 и кратность ребра (Ь _к ,с _к ) равна 1, то полагаем а _к+1 = Ь _к и Ь _к+1 = с _к . Увеличиваем к на 1 и идем к пункту 2.

• c)    Увеличиваем к на 1 (и переходим на пункт 8).

• 8)    Полагаем j = у(к) . Если j <  0 , то идем на пункт 10.

• 9)    Полагаем а _к = u[j] , Ь _к = v[j] , с _к = 0 , r[j] = к и идем на пункт 3.

• 10)    Если ккг = 0 , то полагаем т = к — 1 .

Увеличиваем ккг на 1 . Записываем список троек номеров вершин треугольников из последовательности (1), образующих полученную триангуляцию, в общий список триангуляций (под номером кЪг ).

• 11)    Уменьшаем на 1 кратности ребер треугольников S_m и S_m-1 и полагаем к = т — 1 (тем самым эти треугольники удаляются из списка (1)).

• 12)    При каждом г = 1,2,..., к, при котором г[г] > к, полагаем г[г] = 0.

• 13)    Полагаем j = /(а_к,Ь_к,с_к). Если j > 0, то идем к пункту 4.

• 14)    Если к = 1, то завершаем работу алгоритма.

• 15)    Уменьшаем к на 1. Уменьшаем на 1 кратности ребер треугольника S_k.

3.    Параллельный алгоритм построения триангуляций многоугольника

Идем на пункт 12.

При компьютерной реализации описанного алгоритма необходимо хранить в памяти 8 одномерных массивов и 2 двумерных. Поэтому требуемая память — O(N 2 ) . Однако можно уменьшить эту оценку до O(N ) (за счет некоторого снижения быстродействия).

Пусть F — многоугольник на плоскости; Р С F — конечное множество, содержащее все вершины F, а I — прямая, не содержащая точек Р и пересекающая F. Пусть Т Е Tr(F,P) — триангуляция многоугольника F относительно множества Р. Обозначим через П множество треугольников S Е Т, пересекающих /, а через П — объединение этих треугольников. Тогда П является перегородкой, определяемой тройкой F, Р и /. Прямая I разбивает плоскость на две полуплоскости Н1 и Н2. При г = 1,2 обозначим через Т множество треугольников S Е Т, лежащих в Н^ и не входящих в перегородку П. а через Fe — объединение треугольников, входящих в Т. Тогда Т — триангуляция Fj относительно множества Р П Ft. Таким образом, если задана некоторая триангуляция Т Е Tr(F,P), то можно однозначно определить перегородку П и триангуляции Т1, Т2 многоугольников F1 и F2 относительно множеств F1 ПР и F2 ПР соответственно. Наоборот, по триангуляциям Т1 и Т2 однозначно восстанавливается триангуляция Т — достаточно взять все треугольники, входящие в Т1, Т2 и П.

Следовательно, для построения всех триангуляций Т Е Tt ( F, Р ) можно поступить так: выбрать прямую Z , пересекающую F и не пересекающую Р , а затем перебрать все перегородки, определяемые тройкой F , Р , Z , и для каждой такой перегородки П построить все триангуляции многоугольников F 1 и F 2 (определяемых по F и П ) относительно множеств F 1 П Р и F 2 П Р соответственно. Триангуляции многоугольников F 1 , F 2 можно перечислять независимо друг от друга по описанному выше последовательному алгоритму. Осталось описать алгоритм построения всех перегородок, определяемых тройкой F , Р и Z . Сделаем это.

Заметим, что прямую Z следует выбирать так, чтобы по обе стороны от нее находилось приблизительно одинаковое число точек множества Р . Кроме того, расчеты упрощаются, если эта прямая — горизонтальная или вертикальная. Остановимся на случае горизонтальной прямой.

На каждом шаге алгоритма будет определен набор треугольников вида (1), который можно достроить до перегородки, определяемой многоугольником F , множеством Р и горизонтальной прямой Z . Через крт будем обозначать число всех перегородок. В начале работы алгоритма крт = 0 .

Многоугольник F может быть невыпуклым и потому может пересекать прямую Z по нескольким отрезкам. Нам потребуется список всех ребер многоугольника F , пересекающих прямую Z , отсортированный по возрастанию ж -координаты точки пересечения ребра с прямой Z :

e i ,e 1 ,e 2 ,e 2 ,... ,e _q ,e' _q .                                          (2)

Здесь q — число отрезков, на которые распадается пересечение F П Z . Через t будем обозначать порядковый номер такого отрезка. Если точка движется слева направо по прямой Z , то после пересечения ребра е * она попадает в многоугольник F , а после пересечения ребра е * выходит из него. Остальные обозначения — такие же, как в предыдущем алгоритме.

Алгоритм построения списка горизонтальных перегородок

ДАНО:       многоугольник F на плоскости (не обязательно выпуклый);

множество Р из N точек плоскости, лежащее в F и содержащее все вершины многоугольника F ;

горизонтальная прямая Z , пересекающая многоугольник F и не содержащая точек множества Р .

ПОЛУЧИТЬ: список всех перегородок, определяемых тройкой F , Р и Z .

• 1)    Составляем список ребер (2).

• 2)    Полагаем к = 1, t = 1 и крт = 0.

• 3)    Полагаем a_k = г1 и b_k = г₂, где г1, г₂ — номера вершин ребра е*.

• 4)    Полагаем c_k= 0.

• 5)    Полагаем j = f (a_k,b_k,c_k).

• 6)    Полагаем c_k = j. Если ребро (a_k,c_k) пересекает прямую Z, то полагаем a_k+1 = a_k и b_k+1= c_k. В противном случае полагаем a_k+1 = c_k и b_k+1= b_k.

• 7)    Если ребро (a_k+1,b_k+1) не совпадает с ребром е*, то увеличиваем к на 1 и идем к пункту 4.

• 8)    Если t < q, то t увеличиваем на 1, к увеличиваем на 1 и идем к пункту 3.

• 9)    Увеличиваем крт на 1. Записываем список троек номеров вершин треугольников, составляющих полученную перегородку, в общий список перегородок (под номером крт).

• 10)    Полагаем j = /(a_k,b_k,с_к). Если j > 0, то идем к пункту 6.

• 11)    Если к = 1, то завершаем работу алгоритма.

• 12)    Если ребро (a_k,bk) совпадает с ребром e_t, то уменьшаем t на 1, уменьшаем к на 1 и идем к пункту 10.

• 13)    Уменьшаем к на 1 и идем к пункту 10.

4.    Сравнение параллельного и последовательного алгоритмов

При реализации описанного алгоритма необходимо хранить в памяти только 3 одномерных массива длины N каждый (и список ребер (2), размер которого обычно существенно меньше N ). Поэтому требуемая память — O(N ) .

Рассмотрим вопрос об объеме памяти, необходимой для хранения списка всех триангуляций Т Е Тт(F,Р ) многоугольника F относительно конечного множества Р . Прежде всего надо описать F и Р , для чего можно, например, указать число N элементов множества Р , а затем выписать набор координат ж _г , у точек этого множества, после чего привести список номеров вершин многоугольника F . Информацию же о триангуляциях можно записывать различными способами. Один из них таков. Для каждой триангуляции будем хранить список номеров вершин треугольников, составляющих эту триангуляцию. Тогда список всех триангуляций будет содержать ккг • (3 • N ) чисел в промежутке от 1 до N (напомним, что ktr = | Tt ( F, Р) | — число всех триангуляций многоугольника F относительно множества Р , а m — число треугольников в любой такой триангуляции).

Другой способ заключается в следующем. Пусть П — некоторая перегородка, определяемая многоугольником F , множеством Р и некоторой (заранее выбранной) прямой / . Тогда П однозначно определяет две части F 1 и F 2 многоугольника F (см. начало предыдущего раздела). Нам потребуется разделяющий символ, который обозначим R (за R можно принять, например, число N + 1 ). Фрагмент записи, кодирующий список всех триангуляций Т Е Тт(^Р ) , до которых можно достроить перегородку П , имеет такой вид:

• 1)    Список номеров вершин треугольников, составляющих перегородку П , а затем разделяющий символ R .

• 2)    Число m 1 треугольников в любой триангуляции первой части F 1 многоугольника F .

• 3)    Список триангуляций первой части F 1 многоугольника F . Для каждой триангуляции записывается список номеров вершин треугольников, составляющих эту триангуляцию.

• 4)    Символ R .

• 5)    Число m 2 треугольников в любой триангуляции второй части F 2 многоугольника F .

• 6)    Список триангуляций второй части F 2 многоугольника F (как в пункте 3).

• 7)    Символ R .

Пусть при г = 1, 2 часть F _i многоугольника F имеет t _i триангуляций. Пусть также перегородка П состоит из т _п треугольников. Тогда имеется t 1 • t ₂ триангуляций Т Е Е Tr(F,P ) , до которых можно достроить перегородку П . При этом любая триангуляция состоит из т = т 1 + т _п + т ₂ треугольников. Поэтому для записи этих триангуляций по первому способу необходимо V 1 = (t 1 • t ₂ ) • (3т) = 3t _i t ₂ т чисел в диапазоне от 1 до N . Второй же способ требует

V 2 = (3т п + 1) + (1 + t i • (3т 1 )) + 1 + (1 + t 2 • (3т 2 )) + 1 = 3т п + 3+т 1 + 3t 2 т 2 + 5

чисел. Разность V 1 — V 2 можно записать в виде

V i — V 2 = 3m п (t i t 2 — 1) + 3т 1 t 1 (t 2 — 1) + 3т 2 t 2 (t i — 1) — 5.

Если t 1 t ₂ >  1 и т _п >  2 , то V 1 — V 2 > 0 , поэтому второй способ записи списка триангуляций требует меньше памяти, чем первый. Если же t 1 = t ₂ = 1 , то второй способ требует запомнить на 5 чисел больше, чем первый. Однако это бывает только тогда, когда части F 1 и F 2 многоугольника F допускают только одну триангуляцию каждая. Подобные ситуации случаются, но достаточно редко (см. ниже примеры 2 и 3). В подавляющем большинстве случаев (когда t 1 t ₂ >  2 ) V 2 меньше V 1 :

Утверждение 1. Пусть перегородка П и целое число п >  4 таковы, что каждая из частей F 1 , F 2 многоугольника F содержит по п точек множества P, которые являются вершинами выпуклого п-угольника. Тогда ^ < ^-^ + ₃(_{2 п - 4})5( _С —^2 , где C _k = k+i C _2k — число Каталана (см., например, [9]). В частности, при п = 4 верно ^ 2 <  ⁵ , а при п = 5 выполнено -Я <  ¹ .

V i 8                                         V i      4

Доказательство. Так как части F 1 и F 2 многоугольника F не имеют общих точек, получаем, что N = | Р | >  2п , поэтому число треугольников т в любой триангуляции Т Е Tr(F,P ) не меньше 2п — 4 . Так как выпуклый п -угольник допускает ровно C _n-2 триангуляций (см.: [8; 9]), несложно заключить, что t _i >  C _n-2 при г = 1, 2 . Пусть для определенности 1 <  t 1 <  t ₂ . Тогда V 2 <  3t ₂ (m _п + т 1 + т ₂ ) + 5 = 3t ₂ т + 5 . Поэтому

V 2  3t ₂ т + 51    5      1         5

V i “ 3тt 1 t 2     t i ⁺ 3тt 1 t 2 “ C _n - 2 ⁺ 3(2п — 4)(C _n-2 ) ^{2 .}

Остановимся теперь на вопросе о сравнении быстродействия последовательного и параллельного алгоритмов. Чтобы перечислить все триангуляции Т Е Tr(F,P ) , до которых можно достроить перегородку П , параллельный алгоритм должен построить t 1 и t ₂ триангуляций частей F 1 и F 2 многоугольника F соответственно, а перед этим — саму перегородку П . Таким образом, надо найти 1 + 1 1 +1 ₂ триангуляций отдельных частей многоугольника F . Последовательный же алгоритм должен строить t 1 • t ₂ триангуляций всего многоугольника F . Если t 1 ,t ₂ >  2 , то первое число меньше второго, то есть параллельный алгоритм работает быстрее последовательного.

Если части F 1 и F 2 , определяемые горизонтальной перегородкой П , достаточно велики, то каждую из них можно разбить на две части вертикальной перегородкой и перечислить триангуляции получившихся четырех частей многоугольника F . Ниже (в примере 1) приведены результаты численных экспериментов.

Приведем теперь результаты, полученные с помощью описанных алгоритмов.

Пример 1. Рассмотрим на плоскости множество из п • т точек:

Lm,n = {(м) : г = 1, 2,...,п, ] = 1, 2,...,т}, где п, т > 1 — целые числа. Пусть F — выпуклая оболочка множества Р = Lm,n. Число триангуляций в Tr(F1 Р) при некоторых п и т подсчитывалось тремя способами: с помощью последовательного алгоритма (алгоритм 1), по алгоритму с одной горизонтальной перегородкой (алгоритм 2), а также по алгоритму с одной горизонтальной и двумя вертикальными перегородками (алгоритм 3). Получены следующие результаты:

п	3	4	4	4
т	6	4	5	6
Алгоритм 1	12	6	3963	Более 2 · 10 5
Алгоритм 2	7	3	85	3 511
Алгоритм 3	2	2	40	1 231
Число триангуляций	182 132	46 456	2 822 648	182 881 520

В таблице указано время работы компьютерной программы (в секундах).

Рассмотрим теперь примеры перегородок, для которых числа t 1 , t ₂ малы и потому параллельный алгоритм не дает существенного преимущества по сравнению с последовательным (примеры 2 и 3), или же, наоборот, эти числа велики и преимущество очень существенно (пример 4).

Пример 2. Пусть F и Р — такие, как в примере 1. Выберем прямую I с уравнением у = 5/2 . При г = 1, 2,... ,п — 1 проведем отрезки, соединяющие точки с координатами (г, 1) и (г + 1,т) . Эти отрезки можно единственным образом дополнить другими отрезками так, чтобы получилась триангуляция многоугольника F отноcительно множества Р . Соответствующая этой триангуляции перегородка изображена (при п = 4 и т = 5 ) на рисунке 2 слева (входящие в нее треугольники заштрихованы). Для этой перегородки t 1 = t 2 = 1 .

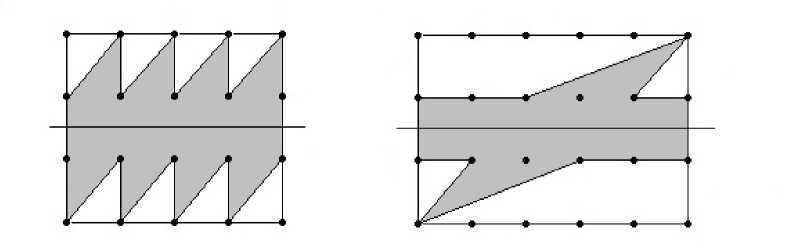
Рис. 2. Многоугольники из примера 2 ( слева ) и примера 3 ( справа ), а также перегородки, соответствующие описанным в этих примерах триангуляциям

Пример 3. Пусть снова F и Р — такие, как в примере 1, причем т = 4, а п имеет вид п = 6к или п = 6к + 2, где к > 1 — целое. Пусть I — прямая с уравнением у = 5/2. Пусть также I — отрезок, соединяющий точки q1 и q2 с координатами (1,1) и (п, 4) соответственно. Пусть 11 — множество отрезков с концами q1 и р, где точка р принадлежит множеству Р и лежит ниже отрезка I. Пусть также 12 — множество отрезков с концами q2 и р, где р Е Р и точка р лежит выше отрезка I. Тогда множество отрезков Z1 U Z2 U {7} можно единственным образом дополнить другими отрезками так, чтобы получилась триангуляция многоугольника F относительно множества Р. Пусть Π — соответствующая перегородка и Π — объединение треугольников из Π. Если начать обход границы многоугольника Π (против часовой стрелки) из вершины q1, то встретятся вершины с координатами (^ + 1, 2), (п, 2), (п, 3), ([2у1] , 3)), q2 = = (п, 4), ([^+1] , 3)), (1, 3), (1, 2), ([^j2] , 2)), после чего мы вернемся в вершину q1. Соответствующая этой триангуляции перегородка изображена (при п = 6) на рисунке 2 справа (входящие в нее треугольники заштрихованы). Для этой перегородки t1 = t2 = 1.

Пример 4. Пусть F и Р — такие, как в примере 1, причем п = 5 и т = 6 . Пусть П — перегородка, заполняющая горизонтальную полосу 3 <  у <  4 . Тогда части F 1 и F 2 многоугольника F будут иметь по 12 170 триангуляций каждая и отношение р 2 будет меньше числа 0 , 0001 .

Пример 5. Пусть т, п >  1 — целые числа, а F и Р — многоугольник и множество из примера 1 для этих т и п . Пусть V 1 и V 2 — количество целых чисел (в границах от 1 до N + 1 , где N = т • п ) при первом и втором способе записи списка всех триангуляций многоугольника F относительно множества Р . В следующей таблице указаны приближенные значения V 1 и V 2 (а также их отношение) при некоторых т и п :

п	3	4	4	4
т	6	4	5	6
Число триангуляций	182 132	46 456	2 822 648	182 881 520
Число V 1	10, 93 • 10 6	2,51 • 10 6	203, 23 • 10 6	164,6 • 10 8
Число V 2	0,82 • 10 6	0, 29 • 10 6	9,18 • 10 6	2,67 • 10 8
̃︁ Отношение 2 и	0,075	0,115	0, 045	0,016

Пример 6. При перечислении триангуляций можно учитывать только те из них, в которых нет треугольников с длинными сторонами или же треугольников с маленькими углами (задача фильтрации). Укажем число триангуляций многоугольника из примера 1, для которых длины всех сторон треугольников не больше заданного числа L :

п	3	4	4	4
т	6	4	5	6
L = 2	1 024	512	4096	32 768
L = 3	84 592	28 608	1 168 516	47 733 448
L = 4	163 330	46 456	2 700 598	159 422 068