О периодических решениях функционально-дифференциального уравнения третьего порядка

Рассмотрим периодическую краевую задачу        для         функционально дифференциального уравнения: 2

^{x ( t} ) + ⁽ RX ⁾⁽ t ) + j g i ⁽ t ) X⁽ i ) (^T i ⁽ t ) ) = f ⁽ t )  ⁽¹⁾

x(0) = x(l), X(0) = x(l), x(0) = x(l)      (2)

где R: Wp 3 ^ Lp - линейный ограниченный оператор,      Ti : [0, l] ^ [0, l],      t e L^, gi, f: [0;lb R , gi, f eLp, i = 02.

Введем в рассмотрение пространства.

Пусть L p = L p [ 0; l ] - пространство суммируемых в p -ой степени функций x :[0, l ] ^ R ; W_p ,3 = W p ,₃ [ 0; l ] - пространство абсолютно непрерывных вместе с третьей производной функций x :[0, l ] ^ R 1 , таких, что x '"e L p , с нормой

II4,, =| x (0)1 +1 x (0)l +l x («) +1 x iL .

p ,3                                                               p

Определение. Под решением задачи (1), (2) будем понимать всякую функцию x e Wp,3 [0; l ], удовлетворяющую почти всюду на

[0; l] уравнению (1) и периодическим краевым условиям задачи (2).

Обозначим через W °₃ пространство: W p ⁰3 = { x e W p ,3 [ 0; l ] / x ( 0 ) = x ( l ), x ( 0 ) = x ( l ), x ( 0 ) = x ( l )} .

Запишем задачу (1), (2) в пространстве W °₃ в виде операторного уравнения

Lx = Fx ,             (3)

где операторы L , F : W_p ’₃ ^ L_p определяются следующим образом: Lx = x ,

^Fx = ^{- (} Rx ⁾⁽ t ) — j g i ⁽ t ) x ⁽ i ) ⁽ t ⁽ t ) ) ^{+ f (} t ) .

i =0

Вспомогательные утверждения.

Приведем необходимые в работе вспомогательные утверждения.

Для линейного оператора L : X ^ Y через imL и ker L соответственно обозначим образ и ядро оператора L .

Лемма 1. Ядро и образ оператора L : Wp 3 ^ Lp определяются равенствами ker L = {x e Wp’3 / x (t) = C, C e R},

l

imL = {y e Lp / j y(t^t = 0}.

Доказательство. Справедливость первого равенства леммы проверяется непосредственно.

Проверим справедливость второго равенства. Для этого воспользуемся представлением решения уравнения в виде x (t) = C,t2 + C2t + C3 +1 j (t - s )2 y (s )ds.

Применив периодические краевые ус-l ловия, получим j y (tyr = 0.

Лемма доказана.

• 1)    LK_p = 1 ₀ , где I _o : imL ^ Y - естественное вложение;

• 2)    K p Lx = P^cx для любого x g X ;

• 3)    P c K p = K p .

Лемма 3. Обобщенно обратный для оператора ( Lx ) ( t ) = x ( t ) , ассоциированный с проектором P (6), имеет вид

Определение. Линейный оператор P : X ^ X называется проектором , если P ² = P .

Нам потребуются проекторы на ядро и образ оператора L .

Лемма 2. Операторы P : W_p ’₃ ^ W_{p 3} и Q : L p ^ L p , определяемые равенствами

Px = x (0) ,             (4)

l

^Qy = У -y f У ^{( s} )d^s ,         ⁽⁵⁾

l 0

являются проекторами соответственно на ядро и образ оператора L .

Доказательство. Справедливость равенства P ² = P очевидна.

Для доказательства второго утверждения достаточно проверить, что оператор (дополнительный проектор) Q C = I — Q , определенный равенством

l

^Q С y = yf y ^{( s} ) d^{s ,} l 0

является проектором. Действительно, ll qCQCy)=yf yfy(s)ds dt = QCy.

l 0 у l 0           у

Это означает, что оператор Q C является проектором, называемым дополнительным к Q .

Равенство imQ = imL очевидно.

Лемма доказана.

Определение     [1].     Оператор

K_p : imL ^ X будем называть обобщенно обратным к оператору L : X У Y , ассоциированным с проектором Р, если справедливы равенства:

^K P y = ¹ f ^{( t — s )2} y ^{( s} )d^{s +}

² 0

^—yy f ^{s 2} y ^{( s} ) ds .

²¹ 0

( t ² t

— +- _ч2/ 2

—

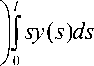
Доказательство. Проверим равенство LK p = I :

d ³ (I t-

LK p у = У1 2 ^{f ( t} - s ' ^{y (} sds

—

—

у

у

t ¹              1

— f ^{s 2} y ⁽ s ) ds 1 = y ⁽ t ).

² l 0            J

Проверим выполнение равенства

K_pLx = P^cx .

K_PLx =— j ( t — s )² x' ( s ) ds + 20

(t2    t yy+y If sx (s )ds— у 2 l 2 J 0

—

t ^l

— j s x s ) ds = 2 1 0

2 t\f

+ 2/ ⁺ 2

у ^{2 1  2} Д

—

l

— | ( t — s ) ² x ( s )| + 2J" ( t — s ) x ( s ) ds | +

² у                ¹⁰     0                  J

l

\

^sx(s )| 0 ^—f ^{x ( s} )d^{s —} yy ^{( s 2 x ( s} ) л              ² l

J

l

—

\

² f ^{sx ( s} ) ^ds = ⁽ t ^{— s} ) ^{x ( s} )l 0 +

J

у

t

\

J

+

t

+- l

l

\

J

= P C x .

Выполнение равенства P^cK_p = K_p очевидно. Лемма доказана.

Лемма 4. Для оператора K_P справедлива оценка:

II ^K P ^y W °, ^р ,-

<

(,   ( l           ¹      l      ¹   1

1 + 1+ 1 Iq1q у у 2 J'y q +1  2]2 q +1J

y _{L P}

Доказательство. Имеем

l

C

+i bt И

к

l f s4ds + — q

1       2l^

+-- l

l

I s ² y ( s ) ds +

I s2 qds+1 14, =

⁰            J

1+

к

l j i

--+ 1 Iq--+ q

l }

2 Л q + 1  p q + 1 J

y LP

Лемма доказана.

Соответствующее выбранным проекторам P и Q разложение пространств представим в виде

W_p, ₃ = ker L Ф X _o, L_p = imL Ф Y .

Оператору L поставим в соответствие линейный ограниченный сюръективны1й оператор

L _o : W_P ’,з ^ imL , Lx = Lx, x g W_p и обозначим через L * сопряженный к L оператор.

Для определения условий разрешимости уравнения (3), а следовательно, и задачи (1), (2) воспользуемся следующей теоремой.

Теорема 1 [3]. Пусть выполнены условия:

• 1)    L - нетеров;

• 2)    F - вполне непрерывен;

• 3)    существуют такие числа у , 8 >  0 , что для каждого элемента х 0 g Х 0 существует элемент u g ker L , удовлетворяющий требованиям F ( x ₀ + u ) g imL , | u || <  /|| x ₀1| + 8 ;

• 4)    b ( F )(1 + у ) <  q ( L ) .

Тогда уравнение (3) имеет хотя бы одно решение.

Лемма 6. Для любого элемента x(t ) g W 0₃ справедливы неравенства

Определение [2]. Относительным коэффициентом сюръективности оператора L назовем число q ( L ) , определяемое равенством

L Ml q (L) = infVir, z g (imL) .

^{z #0}    \\^z\\

I ^{x (} t ) <  k o| W W V ^p ,³

I ^{x (} r ⁽ t Bl <  k o|| x || 0 p •

I x ( ^T ( t ))| <  k J| x | 0.

p ,-

I ^{x ( T (} t B| <  ^k 2 || x || 0

p ,

где

l ² l ² k_n = max<1; l ;—;— q ⁰       \    2  2^2 q + 1

l

f ,

Для оценки коэффициента сюръективности оператора L нам потребуется

Лемма 5 [2]. Пусть L : X ^ Y - линейный ограниченный нормально разрешимый оператор, ядро которого дополняемо. Для любого ограниченного проектора P : X ^ X на ker L обобщенно обратный K_P : imL ^ X к оператору L ограничен, причем норма оператора K удовлетворяет неравенству

I K p | r' <  q ( L ) .

Определение [2]. Если оператор F : X ^ Y ограничен на ограниченных подмножествах и

b ( F ) = lim       Y < да ,

¹xx - H x

то он называется квазиограниченным , а число b ( F ) - квазинормой оператора F .

l

k, = max \ 1; l ; l q

[     q ++1

> , k₂ = max

Доказательство. Докажем первое неравенство, используя представление

21B x (t) = —x (0) + tx(0) + x (0) + — [(t - s )2 x (s )ds.

2                       2J0

Имеем

I x ( t )| < -| x (0)| + lx (0)| + | x (0)| +

f t-                   1 q 2²

+ -|| x • ( s )| \_L \ | ( t - s )² q ds f <  Lx (0)| + lx (0)| + | x (0)| + ²         p Л                  ²

где

+

l2 qL

2 q/ 2 q + 1

I^{1 x} ' ^{( s} ) L <  ^k o| l ^x L0 , p                     ^p ,³

l ² l ²

X = max^ 1; l; —; — q----->.

⁰         [     2  2\2 q + 1 J

Аналогично доказываются остальные неравенства. Лемма доказана.

Лемма 7. Для оператора F справедлива оценка Fx ^ <  a + bx W где а = | ff ( t )|| L , 2

b = Ё Mgx t) L +1 HL • i =0

Выразим u из уравнения, в результате

получим

^u = =---- z j I ^{f (} t ) ^{- (} Rx ^{)( t} ) ^- Ё g i ⁽ t ) ^{x (}) ^{T (} t ) ) I ^dt .

g 0 + r 0 I                    i = 0                  J

Таким образом, в качестве оператора

Доказательство. Действительно,

I FA,, <

-(Rx)(t) - Ё gi(t) x(1’T (t))+ i=0

Т: W°д ^ W0 д возьмем оператор p,3

1    l/

^Tx = ^— =----z J I ^{( Rx )( t} ) ⁺ Ё g i ⁽ t ) ^{x (}) ^{т (} t ) ) I ^dt .

g 0 + r 0 k           i=0

p ,3

—

Найдем оценку Tx

+ ^{f (} t )i _L ^{f (} t )i _L + ⁽tM g ,⁽ t )i _L +i R L ) x i w ₃.

p                  p        ■ n                   p             p          p ,3

i = 0

Лемма доказана.

i TxW, =     '

p     |g 0 ⁺ r|

l

W

J ^{(( Rx} )⁽ t ) ⁺ Ё g i ⁽ t ) ^x(i ) ^{T (} t ) ) dt <

i = 0

Для проверки выполнения третьего условия теоремы 1 рассмотрим уравнение

Q^CF ( x + u ) = 0, где u e ker L , x - некоторый элемент X _o. Если при каждом фиксированном x e X_o данное уравнение имеет решение, то существует оператор T , удовлетворяющий условию F ( x + Tx ) e imL .

<^-- 1

I g 0 ⁺ r

где

\

IRL +Ё Ш(' X L x|| p     i=0               p J

q y=Л IIRl,

I g 0 ^{+ r} | ^k

Лемма доказана.

p

W p., = ^Y Щ,, ’

+ E ki||gi(*)llL i=0                   ‘

\

' p J

Лемма 8. Пусть выполнены условия ll j f (t)dt = 0 и J (R(1)(t) + go(t))dt ^ 0, тогда 0                       0

оператор Т : W °₃ ^ W_p ’₃ , удовлетворяющий условию F ( x + Tx ) e imL , имеет вид

Теорема 2. Пусть выполнены следующие условия: l

1) j f ( t ) dt = 0;

l

2) j ( R(1)(t ) + g ₀( t))dt ^ 0 ;

Tx =—=—z j I ^{( Rx)(t} ) ⁺Ё g , ⁽ t ) ^{x (}’ ^{т (} t ) ) I ^dt , g 0 + r 0 Л            i = 0                   J

3) b(1 + у)k < 1, где b = £ki||gi(t)|Il +|RL , 7 = JlL i=0              p          p          |g 0 + r|

где g 0 =j g0(t)dt, r =j R(1)(t)dt. Причем 0

справедлива оценка

IITxWf3 < Yx W 3, p,3

где y = ⁽ R L ^{+ k} 'I g ⁽ t ) L )

Ig 0 + r| pp

l ² l ²

k_n = max; I; l ; —; — q        _f,

⁰         [     2  2^2 q + 1 ’

l

^k 1

l

= max< ! 1; l ; l ^q

.      q + ^{+ 1}

g 0 =

l

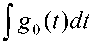
> , k₂ = max

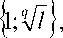
l

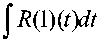
Доказательство. Рассмотрим уравнение

l

QF (x + u) = - j (f (t) - (Rx)(t) - uR (1)(t) - l 0

k = 1 + | l + 1 | q

1 2 A

lll --1—q----- q +1  2 Y 2 q +1

.

2                 Л

^- ug 0 ⁽ t ) ^-Ё g i ⁽ t ) ^x(i ) ^Т(t ) ) ^dt = 0.

i = 0                     J

Тогда задача (1), (2) имеет хотя бы одно решение в пространстве W_p ,₃ .

Доказательство. Выполнение первых двух условий теоремы 1 очевидно.

Справедливость условия 3) следует из леммы 8.

Пользуясь леммами 4 и 5, получим

(          Г^Т1

q ( L ) >   1 +1 —+ 1 | q 1 q .

^  12 Д/ q +1  2pq +1 J

Из леммы 7 следует, что b ( F ) = b .

Таким образом, выполнение условия 4 теоремы 1 автоматически следует из условия 3 данной теоремы. Теорема доказана.

В качестве примера рассмотрим задачу:

xY ) + ¹ x⁽ t) ^{+ 1} x ⁽ t) ^{+ 1} x ^ t J = f ⁽ t) ,

x

(o)=x IП), x(0)=4 П) x(0)=4 П где f (t) = ^cos(4t)+ ^^ sin(8t)-ycos(8t).

Данная задача удовлетворяет условиям теоремы 2 и имеет периодическое решение x ( t ) = cos ( 8 t ) .