О периодических решениях обыкновенного дифференциального уравнения третьего порядка

Рассмотрим периодическую краевую задачу для обыкновенного дифференциального уравнения:

x '"( t ) = f ( t , x ( t ), x '( t ), x "( t)) + g(t ),     (1)

x ( 0 ) = x(l ), x '( 0 ) = x'll ), x "( 0 ) = x"(l ), (2) где t g [ 0; l ] , функция g : [ 0; l ] ^ R ограничена в существенном, f : [ 0; l ] x R ³ ^ R¹ удовлетворяет условию Каратеодори.

Введем в рассмотрение пространства.

Пусть Lp = Lp [0; l ]  - пространство суммируемых в p -ой степени функций x :[0, l] ^ R ; Wp,3 = Wp,3 [0; l] - пространство абсолютно непрерывных вместе с третьей производной функций x :[0, l] ^ R', таких, что x"' g Lp , с нормой

II x r, = x (0)1 + x ’(0)1 + x '(0)1 +1 x "( t 1 . p ,3                                                                             p

Определение. Под решением задачи (1), (2) будем понимать всякую функцию

x g W p ,3 [ 0; l ] , удовлетворяющую почти всюду на [ 0; l ] уравнению (1) и периодическим краевым условиям задачи (2).

Обозначим через W ⁰ пространство:

Wp03 = {x g Wp,3 [0; l]/x(0) = x(l), x'(0) = x'll\ x "(0) = x"(!)}.

Запишем задачу (1), (2) в пространстве W ⁰ в виде операторного уравнения

Lx = Fx ,              (3)

где операторы L, F : W_p ’₃ ^ L_p определяются следующим образом:

( Lx )( t ) = x '"( t ) ,

( Fx )( t ) = f ( t , x ( t ), x '( t ), x "( t )) + g ( t ).

Приведем необходимые в работе вспомогательные утверждения.

Для линейного оператора L : X ^ Y через imL и ker L соответственно обозначим образ и ядро оператора L .

Определение. Линейный оператор P : X ^ X называется проектором , если P ² = P .

Лемма 1 . Ядро и образ оператора

L : W_p 0з ^ L_p определяются равенствами:

ker L = { x е W ° ₃ / x ( t ) = C , C e R } ,

l imL = {y e Lp / j y(Cd? = 0}.

Операторы     P: Wp’3 ^ Wp’3

Q : L p ^ L p , определяемые равенствами

Px = x (0),(4)

l

Qy = У-yf У(s )ds , l 0

являются проекторами соответственно на ядро и образ оператора L .

Доказательство. Справедливость первого равенства леммы очевидна.

Проверим справедливость второго равенства. Для этого воспользуемся представлением решения уравнения x (t) = У (t)

в виде:

x ( t ) = Ct ² + Ct + C + ¹ j ( t - s ) ² y ( s )ds .

2^J o

Определение     [1].     Оператор

K_p : imL ^ X будем называть обобщенно обратным к оператору L : X ^ Y , ассоциированным с проектором Р, если справедливы равенства:

• 1)    LK_p = 1 ₀, где 1 ₀ : imL ^ Y - естественное вложение;

• 2)    K p Lx = P^cx для любого x е X ;

• 3)    P c K p = K p .

Лемма 2. Обобщенно обратный для оператора ⁽ Lx ) ( t ) = x '"( t ) , ассоциированный с проектором P (4) имеет вид

^K P y =

1 Г           7

= yj ⁽ t ^{— s} ) y ^{( s} ) ^{ds +}

² 0

tl

^——j^{s 2} y ^{( s} ) ^ds .

^{2 1} 0

и справедлива оценка:

II KPyllw р, •

<

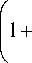
X 2 J \

l

—

Применив периодические краевые ус-

ловия, получим

l j y (t )dr = 0.

Справедливость равенства P ² = P проверяется непосредственно.

Для доказательства второго утверждения достаточно проверить, что оператор (дополнительный проектор) Q^c = I — Q , определенный равенством

l

Q С y=7 J y(s )ds, l 0

является проектором. Действительно,

'.     ‘.          ^

^Q ( Q y ) =~] yj y ^{( s} ) d^{s dt} = ^Q y .

l 0 у l 0           J

Это и означает, что оператор Q C является проектором, называемым дополнительным к Q . Равенство imQ = imL очевидно. Лемма доказана.

l

2 q + 1

) yk -⁽⁶⁾

Доказательство. Проверим справедли-

вость равенства

Имеем

LK_p у =

LK_p = I .

d3 (1 t die (2j (t—s)y(s d+

—

у

у

¹             ^

• ^— —j ^{s 2} у ^{( s} d ^s 1 = у ⁽ t ).

• ² l 0            J

Проверим выполнение равенства K p Lx = P^cx .

K_PLx =

t

f /2

x "'( s ) ds + — + -

У 2 1   2

A

J

j sx "'( s )ds — 0

l

^—i/| ^{s 2 x m( s} ) ^ds = 21 ⁽ t ^{— s ) 2 x}”^(s ^ ⁺

t                       ^

+ 2 j ( t — s ) x "( s )ds

0                 J

+

+

f t ² tУ _V ² 1 ^{+ 2} у

f sx (s)|o

V

У

-j x ( s )ds 0         J

~^f s ² X ”( s )| -

2 l V         ^7|o

l

- 2 j sx"(s ) ds

о           J

f

=   ⁽ t ^{- s} ) x '^{( s} )₀

V

+

У j x '( s ) ds 0          J

+

Лемма 3 [3]. Пусть L : X ^ Y - линейный ограниченный нормально разрешимый оператор, ядро которого дополняемо. Для любого ограниченного проектора P : X ^ X на ker L обобщенно обратный K_p : imL ^ X к оператору L ограничен, причем норма оператора K удовлетворяет неравенству

I Kp\ г¹ s q ( L ) .

+ -

t /              ¹           У

7 ( sx '⁽ s )| 0 ^- J x '⁽ s ) ds = P l

J

■ Cx .

Определение [3]. Если оператор F : X ^ Y ограничен на ограниченных подмножествах и

Выполнение равенства PcK_p = K_p очевидно.

Проверим справедливость оценки (6).

Имеем

b ( F ) = lim       ^Y

¹ xX "“ H x

< ^ ,

l

s 0

l

+

l

J s² y ( s ) ds +

⁺ l U p

V

f, f l

= 1 + 1 - + 1 I q -----+ q

l

V

q

² d

l

J ^{s 2} q ^{ds +1} U p

о

J

2 J^ q + 1 P q + 1 J

14 •

Лемма доказана.

Соответствующие выбранным проекторам P и Q разложения пространств представим в виде

W_p^ ₃ = ker L Ф X _o, L_p = imL © Y _o.

Оператору L поставим в соответствие линейный ограниченный сюръективный оператор

Lo : WP’,3 ^ imL, Lox = Lx, x e Wp\з и обозначим через Lo сопряженный к L оператор.

Определение [3]. Относительным коэффициентом сюръективности оператора L назовем число q ( L ) , определяемое равенством

L o M l             *

q ( L ) = inf^^, z e ( imL ) .

^{z #0} ll ^z ll

Для оценки коэффициента сюръективности оператора L нам потребуется следующее утверждение.

то он называется квазиограниченным , а число b ( F ) - квазинормой оператора F .

Для определения условий разрешимости уравнения (3), а следовательно, и задачи (1), (2), воспользуемся следующей теоремой.

Теорема 1 [2]. Пусть выполнены условия:

• 1)    L - нетеров;

• 2)    F - вполне непрерывен;

• 3)    существуют такие числа у , 5 >  0, что для каждого элемента х о e Х о существует элемент u e ker L такой, удовлетворяющий     требованиям      F ( x ₀ + u ) e imL ,

II u ll ^s M l ^x o|l ^{+ 5 ;}

• 4)    b ( F )(1 + у ) <  q ( L ) .

Тогда уравнение (3) имеет хотя бы одно решение.

Лемма 4. Для любого элемента

x ( t ) e W °₃ справедливы неравенства

Ix(t) '  kollxllwpV p ,3

Ix'(t)| '  k 11 IxWV p ,3

I ^x "⁽ t ) ' ^k 2I x w V ^p ,³

где

k 0

„       , l² l ²       l

= max^ 1; l ; —; — q ------>,

2 2p q + 1 J

k 1

l

= max< 1; l ; l q

V q+ + 1 J

> , k₂ = max

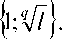
Доказательство. Докажем первое неравенство, используя представление

x ( t ) =

= -x "(0) + tx '(0) + x (0) + ¹ ( t - s )² x ^m( s ) ds .

2             -

Имеем

| x ⁽ t )|

/2

<-| x "(0)1 + l\x ‘ (0)1 + | x (0)| +

sign ( щ ). f ( ’ , щ 1 , щ 2 , щ 3 ) -1| д [_ >  0

⁽ sign ⁽ щ ) f ⁽ ’ , ^щ_р U 2 , U 3 ) ⁺ || g ^ < ⁰⁾ при | щ | >  щ *, щ , щ ₂, щ , щ ₄ е R ¹ и почти всех t е[0, l ] ;

+ —

t

।x '"⁽ s 4 И ⁽ t - s ^{) 2} q ds

<

3) e (1 + k ₀ /1 +( -+ 1 1 ^ ¹ + i q

⁰ \  1 2 Ц q + 1  2p q + 1

l

< 1 ,

p

где в = koa + kb + k2c ,

< -\x "(0)| + l\x ' (0)| + | x (0)| +

⁺w+r¹ x ’^{( s 1} L p <  k ⁰ x *’

l

l ² l ² где k_n = max; I; l ; —;— q ⁰       |    2 2p q + 1

> .

Аналогично доказываются остальные неравенства. Лемма доказана .

Лемма 5. Пусть существуют неотрицательные постоянные a, b, c и неотрицатель ная функция   h(•) е Lm [0, l],  такие, что

| f ( t , щ , u ₂, u ₃ )| <  ^щ | + Ь|щ₂ 1 + c|u ₃1 + h(t ) почти всюду при t е [0, l ] и щ , щ₂ , щ з е R 1 .

Тогда для оператора F справедлива оценка

II Fx L <  ^{а + в} x k г p                          ^p ,3

где а = p l (| h^_L +1| g ||_£ ), в = k ₀ a + k 1 b + k ₂ c .

Доказательство. Действительно,

II Fx^ < ( ax ⁽ t )|+ bx '( t ) + cx "( t )|+ h ( t ) + g ( t ) l <  <  p ^ ⁽l h L ⁺ 1 g L.^{) +( k} 0 ^{a + k} i ^{b + k} 2 ^c II x k , _s •

Лемма доказана.

Перейдем к формулировке основного результата статьи.

Теорема 2. Пусть выполнены следующие условия:

• 1)    существуют неотрицательные постоянные a , b , c и неотрицательная функция h ( • ) е L [0, l ], такие, что

• | f (t, щ, u2, щ )| < Ощ | + b|u21 + c|u31 + h(t) при щ, щ2, щ3 е R1 и почти всех t е [0,l];

• 2)    существует щ * >  0 , такое, что

  l

  
  

l ² l ²

k_n = max 1; l ; —; — q ⁰        [     2  2^2 q + 1

> , k₂ = max 1; q/l } .

l

• k, = max; 1; l ; l q

1 V q++1J

Тогда задача (1), (2) имеет хотя бы одно решение в пространстве W_p ,₃ .

Доказательство. Для доказательства теоремы проверим выполнение условий теоремы 1. Первые два условия выполнены. Действительно, оператор L - фредгольмов (лемма 1) и оператор F : W_p ’₃ ^ L_p , определенный равенством

( Fx )( t ) = f ( t , x ( t ), x '( t ), x "( t )) + g ( t ), вполне непрерывен.

Для проверки выполнения условия 3) теоремы 1 рассмотрим уравнение

QCF (x + щ) = 0, где щ е ker L, x - некоторый элемент Xo. Если при каждом фиксированном x е Хо дан- ное уравнение имеет решение, то существует элемент щ е kerL, удовлетворяющий условию F (x0 + щ) е imL .

Произвольно зафиксируем элемент x е X_o и определим непрерывное отображение Ф : R ¹ ^ R ¹ равенством

Ф( С) = ll

= j f (t, x (t) + C, x'(t), x"(t)) dt + j g (t) dt. 00

Далее мы воспользуемся следующим двойным неравенством

- ^k 0I x k \₃<  ^{x (} ’ ) <  ^k 0I x k у ’ ^{е [0, l ]}

(см. лемму 4). Положим C = щ * + k0||x|| p,3

Тогда для всех C >  C 1    справедливо

x(t ) + C >  u * , а следовательно Ф ( C ) >  0. Аналогично Ф ( C ) <  0 для всех

C < C 2 = -и * - ко| Щ .

Тогда в силу непрерывности функции ф существует константа С = C(x), удовлетво- ряющая неравенству

I C l <  max{ | C 1| , | C ₂| } <  к o|| x||      + и * ,

Wp ,3

такая, что Ф ( C ) = 0 .

Таким образом существует элемент ~

C = и e ker L , удовлетворяющий требованиям F ( x ₀ + и ) e imL , || u || <  Y|x ₀1| + 3 , причем Y = к 0 , 3 = и * .

В случае, когда выполнено условие sign ( и 1 ) f ( t , и 1 , и ₂ , и 3 ) + || g ||_£<  0 , доказательство проводится по той же схеме.

Выполнение четвертого условия теоремы 1 следует из условия 3) теоремы 2. Теорема доказана.

Замечание . Возможен и следующий вариант применения теоремы 2. Если отрезок [ 0; l ] не зафиксирован и требуется найти такое значение l , при котором существует решение задачи (1), (2), то за счет подбора (например, уменьшения значения l ) можно добиться выполнения условия 3) теоремы 2.