О подходе к генерации аналитических моделей на основе визуальных моделей бизнес-процессов

Эффективное управление предприятиями и организациями невозможно без использования информационных и аналитических систем, которые создаются и функционируют на основе разрабатываемых аналитиками моделей. Понятие моделирования включает две задачи: создание модели (ее описание в математических терминах или в нотациях языков моделирования) и ее исследование с помощью тех средств, которые отвечают потребностям аналитиков, позволяют решить задачи поддержки принятия решений.

В настоящее время существует множество различных нотаций, которые могут применяться для разработки графических моделей бизнес-процессов, применяемых для решения различных задач: IDEF0 – для отображения логических связей между операциями; DFD – для представления потоков данных; eEPC – для описания процессов, управляемых событиями, и т.д. Для разработки визуальных моделей используются различные инструментальные средства, графические редакторы.

Выбор средств моделирования чаще всего диктует и выбор языка, применяемого для построения моделей. Одни и те же систе-

мы, процессы могут быть описаны на разных языках – в зависимости от того, для решения каких задач строятся модели. При этом аналитики вынуждены, переходя от решения одной задачи к другой, заново строить модели исследуемых объектов.

Для проведения всестороннего анализа моделей с применением различных математических пакетов (Matlab, Maple, MathCAD и пр.) необходимо построить аналитические модели в соответствующих терминах и форматах, применяемых в этих системах. При этом построение аналитических или численных моделей для систем большой размерности с целью проведения их анализа с помощью математических пакетов может стать нетривиальной задачей: помимо масштаба модели другой возможной причиной затруднений перехода к аналитическому представлению графических моделей бизнес-процессов может стать недостаток необходимых для создания модели данных.

Если описана модель бизнес-процесса большой размерности, представленная в какой-либо графической нотации, то переход к соответствующей аналитической модели, которая будет применена для дальнейшего исследования, может быть автоматизирован.

Существуют частные решения задачи преобразования моделей процессов и систем, основанные на применении сетей Петри [3, 21], имитационных моделей [4], специальных механизмов преобразования графических моделей [16, 17, 18].

В данной работе представлены результаты решения следующих задач, связанных с преобразованием моделей для проведения многоаспектного анализа бизнес-процессов:

• 1)    разработка абстрактной графовой модели для промежуточного представления исследуемых бизнес-процессов, генерируемой на основе моделей, создаваемых аналитиками в нотациях применяемых ими визуальных языков моделирования бизнес-процессов;

• 2)    разработка алгоритмов трансформации абстрактной графовой модели, аналитические модели (в одноцветную сеть Петри и модель системы массового обслуживания);

• 3)    расширение возможностей математического пакета средствами генерации и анализа построенных моделей.

Построенные с помощью представленных средств модели дают достаточно полное представление об исследуемых бизнес-процессах. Их анализ может быть выполнен средствами различных математических пакетов.

Схема построения и анализа моделей

С учетом существующих методов преобразования графических моделей бизнес-процессов, разработанных в различных нотациях, предлагается общая схема получения графовых моделей бизнес-процессов, основанная на нормализации и формировании их универсального внутреннего представления, которое может быть преобразовано в различные аналитические формы.

Предлагаемый подход включает следующие шаги:

• 1)    разработка аналитиком графической модели бизнес-процесса в терминах используемого им визуального языка моделирования;

• 2)    выполнение проверки соответствия построенной модели требованиям, которые предъявляются к нормализованной модели;

• 3)    в случае несоответствия графической модели требованиям выполняется ее нормализация;

• 4)    формирование специального промежуточного представления бизнес-процесса на основе полученной нормализованной графической модели (экспорт модели);

• 5)    разбор и загрузка промежуточного представления модели бизнес-процесса в среду выбранного для анализа бизнес-процесса математического программного пакета;

• 6)    доопределение модели (в частности, определение управляемых параметров модели) в среде используемого математического пакета;

• 7)    перевод созданного промежуточного представления модели бизнес-процесса в систему уравнений в используемой среде математического пакета;

• 8)    численное или символьное решение системы уравнений, полученной на предыдущем этапе;

• 9)    формирование отчета о выполнении анализа бизнес-процесса (вывод и анализ результатов решения сформированной системы уравнений).

Данная последовательность действий опирается на реализацию алгоритмов получения графовых моделей в аналитической форме на основе исходных визуальных (графических) моделей, определенных с помощью какого-либо языка моделирования бизнес-процессов.

Выбор графической нотациидля моделирования бизнес-процессов

Для того чтобы разработать и провести апробацию метода трансформации графических моделей бизнес-процессов в аналитические, необходимо выбрать визуальный язык, с помощью которого аналитик может создавать модели бизнес-процессов.

При выборе нотации следует учесть:

• 1)    возможность получения формального описания бизнес-процессов в выбранной нотации;

• 2)    необходимость внесения изменений в построенную модель, ее доопределения для обработки средствами математических программных пакетов;

• 3)    возможность разработки понятного для конечного пользователя алгоритма доопределения модели (задания управляемых параметров моделирования бизнес-процесса).

Результаты проведенного сравнения по данным критериям приведены в табл. 1.

На основании результатов анализа выбрана нотация, описывающая потоки данных, – DFD [14]. Данная нотация выбрана еще и потому, что на данный момент она не являет- ся самой "популярной" при разработке моделей бизнес-процессов и имеющиеся средства визуального моделирования предлагают достаточно узкий спектр исследования моделей в данной нотации. В основном для анализа бизнес-процессов используются диаграммы UML [8, 9, 10, 11, 15], IDEF3 [12, 13, 19], eEPC [4, 7] и пр., отражающие динамику потоков работ, цепочки событий. Хотя, как показал анализ, из модели бизнес-процесса в нотации DFD также можно извлечь информацию, которая может быть полезна при принятии тех или иных управленческих решений на основе ее анализа.

Таблица 1. Сравнительный анализ нотаций моделирования бизнес-процессов

Нотация	Возможные показатели для исследования	Математический аппарат для исследования моделей
IDEF0	1)    время выполнения операций; 2)    временная загрузка исполнителей; 3)    стоимостные оценки операций; 4)    вероятностные оценки сценариев	системы алгебраических уравнений; системы дифференциальных уравнений
IDEF3	1)    время выполнения операций; 2)    стоимостные оценки операций; 3)    вероятностные оценки сценариев	средства имитационного моделирования; системы алгебраических уравнений; системы дифференциальных уравнений; вероятностные математические модели; экономические модели оценки затрат
DFD	1)    время выполнения операций; 2)    стоимостные оценки операций; 3)    количество и время обращений к базам данных; 4)    временная загрузка исполнителей и внешних сущностей; 5)    временные характеристики потоков данных; 6)    объем извлеченных/загруженных данных; 7)    вероятностные оценки сценариев (при их наличии)
BPMN	1)    время выполнения операций; 2)    стоимостные оценки операций; 3)    временная загрузка исполнителей; 4)    временные характеристики потока управления; 5)    вероятностные оценки сценариев
eEPC	1)    время выполнения операций; 2)    стоимостные оценки операций; 3)    временная загрузка исполнителей; 4)    вероятностные оценки сценариев

Определение основных показателей для выполнения расчетов при анализе моделей

Ниже перечислены основные параметры, значения которых могут быть заданы или рассчитаны для элементов DFD в ходе обработки аналитического представления модели бизнес-процесса:

• 1)    процесс характеризуют:

• a)    время выполнения, которое складывается из времени, затраченного всеми исполнителями данного процесса;

• b)    затраты ресурсов, которые складываются из постоянных затрат и переменных затрат, зависящих от количества задействованных исполнителей и затраченного ими времени;

• c)    количество запусков процесса, определяемое в общем случае результатами моделирования исходного бизнес-процесса при заданных значениях параметров;

• 2)    поток характеризуют:

• a)    скорость/время продвижения данных (запросов, заявок, результатов выполнения запросов и пр.) по потоку от одного процесса модели к другому либо от одного процесса модели к хранилищу данных и наоборот;

• b)    объем данных, который проходит по рассматриваемому потоку (актуально для потоков, которые соединяют процесс и хранилища данных);

• c)    затраты на работу потока, связанные с организацией канала передачи данных, которые включают в себя как фиксированные затраты, так и переменные;

• 3)    хранилище данных характеризуют:

• a)    количество запросов на выборку данных (заявок на получение данных), которые выполняются процессами модели;

• b)    количество запросов на добавле-ние/обновление данных, которые осуществляются процессами модели;

• c)    объем информации, которая загружается в хранилище данных процессами;

• d)    объем информации, которая извлекается из хранилища данных процессами.

Помимо численных показателей, характеризующих конкретные элементы модели бизнес-процесса, разработанной в нотации DFD, необходимо выделить показатели, которые могут быть рассчитаны на основе описанных выше характеристик (управляемых параметров), характеризующие рассматриваемую DFD-модель бизнес-процесса в целом:

• 1)    общее время выполнения одного экземпляра бизнес-процесса, рассматриваемого в рамках данной модели;

• 2)    общий объем информации, загруженной и извлеченной из хранилищ данных по запросам процессов в ходе реализации одного экземпляра бизнес-процесса;

• 3)    общие издержки, связанные с выполнением одного экземпляра бизнес-процесса, включая постоянные и переменные затраты.

Предметная область была выбрана с учетом использования при выполнении биз-нес-процессов, описанных в нотации DFD, информационных ресурсов.

При реализации приложения, предназначенного для анализа бизнес-процессов, учитывается, что часть характеристик рассматриваемого бизнес-процесса (управляемых параметров) необходимо явно определять пользователю. Зависимые показатели, характеризующие как отдельные элементы модели бизнес-процесса, так и все модели в целом, будут рассчитаны на основе математической модели, которая описана ниже.

Модель бизнес-процесса

Рассмотрим формальные определения основных элементов модели бизнес-процесса, разработанной в терминах графической нотации DFD.

Определение 1. Графическая модель бизнес-процесса M называется DFD-моделью , если она представляет собой ориентированный помеченный граф:

M = (P , D , F ),             (1)

где P = { p 1 ,p 2,..., p n } - множество вершин, представляющих процессы     модели ,

D = { d 1, d 2,..., dm}  - множество вершин, представляющих хранилища данных модели; а множество дуг F , представляющих потоки данных модели, является объединением двух множеств:

F = F _P и F d ,            (2)

где F_p = { f.^p , f , ^p , . , f p ^p } ^- множество дуг, соединяющих вершины-процессы между собой, F d = { f. d , f d , . , f d } ^- множество дуг, соединяющих вершины-процессы и вершины, представляющие хранилища данных модели.

Определение 2. Межпроцессным потоком данных DFD-модели M называется ориентированная дуга f ^р = ( p. , p j ) из подмножества F _P множества F такая, что p,p _} ^e P и p . * p j .

Таким образом, можно определить следующее характеристическое свойство для дуг – элементов множества F _P :

F P = { ( p , p j ) I p , p j ^{e P} , p . * p j ) ^{C P} 2 - ⁽³⁾

Определение 3 . Потоком данных "процесс–хранилище" DFD-модели M называется ориентированная дуга f .d = ( p . , d _j ) из подмножества F _D множества F такая, что p . e P , d _j e D .

Определение 4. Потоком данных "хранилище–процесс" DFD-модели M называется ориентированная дуга f .d = ( d .. ,p _j ) из подмножества F_D множества F такая, что p _j e P , d . e D .

Характеристическое свойство для дуг – элементов множества F _D – определяется следующим образом:

^Fd = { ( p,d j ) | p , ^{e P} , d j ^{e D v}( d , p j ) |

• |    p_j e P , d e d } c P x D и D x P     (4)

Определение 5. Вершина-процесс p из множества P DFD-модели M называется стартовой , если ее полустепень захода равна 0, т. е. d .n ( p. ) = 0. При определении стартового процесса рассматривается подграф M 1 = ( F p , P ).

Определение 6. Вершина-процесс p из множества P DFD-модели M является завершающей , если ее полустепень исхода равна 0, то есть d _out ( p. ) = 0. При определении завершающего процесса также рассматривается подграф M 1 = ( F_p , P ).

Определение 7. Сценарий реализации бизнес-процесса, определенного с помощью DFD-модели M , представляет собой путь в графе M , который соединяет стартовую и завершающую вершину-процесс. Таким образом, сценарий Si представляет собой упорядоченное подмножество (p1,p2,...,pk) множества всех вершин-процессов P, такое что между двумя соседними элементами множества Si проходит межпроцессный поток дан- ных, т.е. следующее множество

{ ( P 1 , P 2 ) , ⁽ P 2 , P 3 ),..., ⁽ P k - 1 , P k ) } является подмножеством множества всех межпроцессных потоков данных F _P .

На рис. 1 представлен пример бизнес-процесса, а на рис. 2 – пример графа DFD-модели M , соответствующий этой визуальной модели бизнес-процесса, построенной в нотации DFD до введения пометок для расчета показателей.

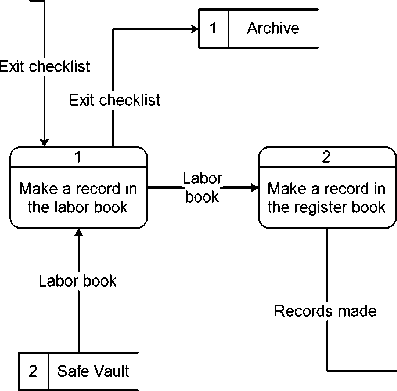
Рис. 1. DFD-модель процесса увольнения сотрудника

Employee's signature

Register book

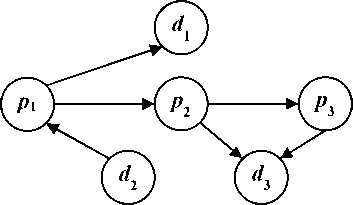
Рис. 2. Граф DFD-модели процесса увольнения сотрудника

Правила нормализации моделей

Как было отмечено, одним из этапов получения аналитического представления для графической модели бизнес-процесса является нормализация, в ходе которой выполняется так называемая валидация модели – проверка на соответствие модели определенным требованиям. Набор правил нормализации задает требования к модели бизнес-процесса в нотации DFD, гарантирующие возможность построения соответствующих аналитических моделей в нескольких форматах, перечислен- ных выше. Правила описываются в представленных выше терминах.

Правило 1. В DFD-модели M может существовать только одна стартовая вершина p_start . В противном случае данная модель M должна быть разделена на несколько моделей, имеющих единственные стартовые вершины.

Правило 2. В DFD-модели M должна существовать, как минимум, одна завершающая вершина p_finish ; в противном случае необходимо ввести дополнительную завершающую вершину-процесс в графе M . Отсутствие завершающей вершины в графе возможно при наличии циклов в графе, поэтому необходимо обеспечить возможность выхода (дуги) из цикла.

Правило 3. В DFD-модели M каждый процесс p_i должен иметь связь, как минимум, с одним другим процессом p_j , то есть ( P i , P j )^v( P j , P i )^G F P . В противном случае вершина-процесс, не имеющая связи с другими вершинами-процессами модели M , должна быть удалена.

Правило 4. В DFD-модели M каждый процесс p_i должен иметь связь, как минимум, с одним хранилищем данных d _j через поток "процесс–хранилище" или "хранилище– процесс", т. е. ( p. , d . ) v ( d j , p i ) e F P . В противном случае вершина-процесс, не имеющая связи с вершинами-хранилищами модели M , должна быть удалена.

Правило 5. В DFD-модели M каждое хранилище данных d_i должно иметь вход-ную/выходную связь (поток данных "процесс–хранилище" или "хранилище–процесс" соответственно) как минимум с одним процессом p_i . В противном случае вершина-хранилище, не имеющая связи с другими вершинами-процессами модели M , должна быть удалена.

Описанные правила составляют основу для программной реализации алгоритмов нормализации исходной модели бизнес-процесса в нотации DFD.

Механизм расчета показателей

Для того чтобы данная модель могла обеспечить процесс расчета основных показателей исследуемого бизнес-процесса, определенных выше, необходимо выполнить дополнительное преобразование графа DFD-модели M , введя пометки дуг и вершин. Формальные определения параметров и правила их доопределения в данной работе не рассматриваются.

При определении механизма расчета введенных выше показателей исходный граф модели необходимо разделить на два подграфа – граф межпроцессных потоков данных

M 1 = (Fp, P) и двудольный граф взаимодей- ствия процессов и хранилищ данных M2 = (FD, P). Пример разбиения графа представлен на рис. 3.

Граф межпроцессных потоков данных используется при анализе сценариев реализации бизнес-процесса, а граф взаимодействия хранилищ данных и процессов – при определении объемов обработанной информации.

Поскольку при реализации исходного бизнес-процесса возможно несколько сценариев, необходимо для каждого межпроцессного потока данных (pi, p.) ввести дополни- тельные пометки Pij , определяющие вероятность перехода по данной дуге.

Вероятность реализации каждого из сценариев Si исходного бизнес-процесса оп- ределяется как

р ( S ) = П P           ⁽⁵⁾

p i , p . с S i , p^ p .

С использованием введенной модели и численных показателей (характеристик процессов) разработан механизм расчета следующих общих показателей рассматриваемой DFD-модели M :

• 1)    T_total – общее время реализации биз-

• нес-процесса, рассматриваемого в рамках данной модели;

• 2)    I_total – общий объем обработанной и переданной по потокам информации в ходе реализации бизнес-процесса;

• 3)    C _total – совокупные издержки, связанные с выполнением рассматриваемого бизнес-процесса.

  

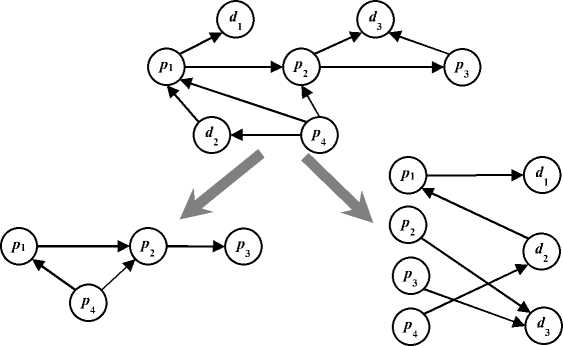
  Рис. 3. Разбиение исходного графа на подграфы

  
  

Прежде чем выполнять расчет данных показателей, выполняется расчет показателей реализации отдельных сценариев исходного бизнес-процесса, на основе которых определяются общие показатели реализации бизнес-процесса, соответствующего DFD-модели M .

Трансформация DFD-модели в сеть Петри

Для получения более точной картины возможных проблем в ходе реализации исход- ного бизнес-процесса, исследуемого с помощью DFD-модели, можно применить одноцветные сети Петри.

Для этого необходимо разработать правила преобразования DFD-модели бизнес-процесса в соответствующую сеть Петри.

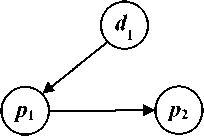
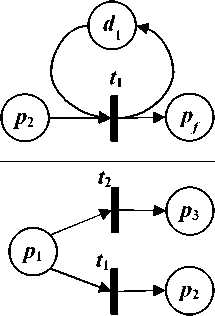
В основе этих правил – соответствие элементов этих двух типов моделей, показанное в табл. 2.

Таблица 2. Соответствие элементов DFD-модели и сети Петри

Интерпретация элемента

DFD-модель

Сеть Петри

Запрос информации из хранилища данных во время выполнения процесса

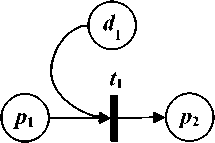
Выгрузка информации в хранилище данных во время реализации процесса

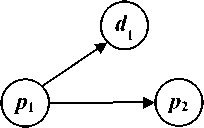
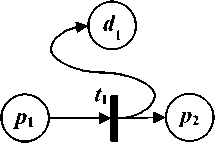
Запрос и выгрузка информации в хранилище данных во время реализации процесса

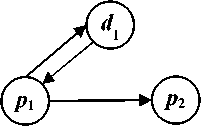
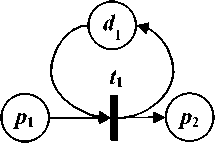
Запрос и/или выгрузка информации в хранилище данных во время реализации завершающего процесса

Альтернативный ход развития исходного бизнес-процесса

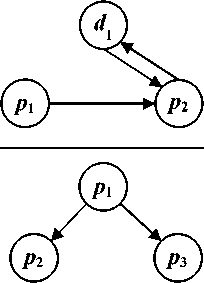
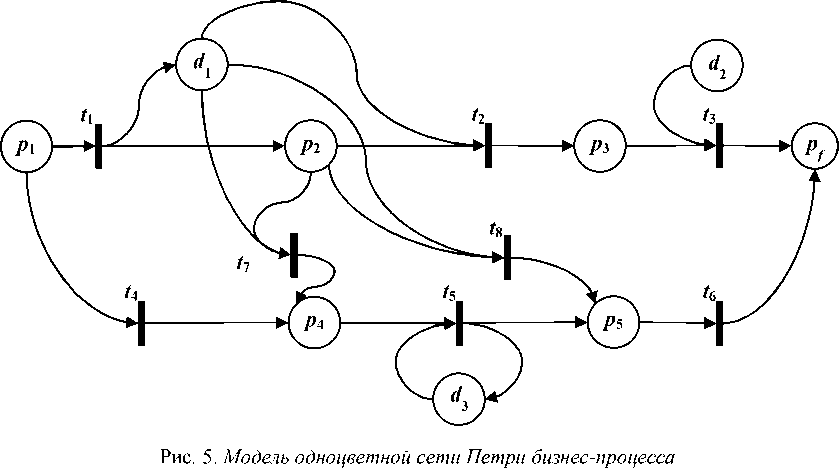
Результат применения правил преобразования DFD-модели, показанной на рис. 4, в одноцветную сеть Петри показан на рис. 5.

С помощью построенной сети Петри можно реализовать дополнительные возможности анализа бизнес-процесса, описанного аналитиком в нотации DFD.

Применение систем массового обслуживания

Описанные выше модели не решают всех задач анализа бизнес-процессов. Другие аспекты реализации процессов, описанных в нотации DFD, можно изучить, используя аппарат систем массового обслуживания (СМО), схемы " гибели " и " размножения " .

В рамках схемы " гибели " и " размножения " определяются вероятности нахождения рассматриваемой системы в одном из n состояний. Состояние системы массового обслуживания S i означает, что если система находится в данном состоянии, то занятыми являются i обслуживающих устройств из всех n доступных.

Разработан метод преобразования модели, который позволяет выполнить анализ бизнес-процесса как СМО, получив в результате вероятности нахождения бизнес-процесса в одном из нескольких состояний, характеризующихся числом занятых обслуживающих устройств.

Полученные результаты могут послужить основанием для принятия решения о проведении реинжиниринга бизнес-процесса, направленного, прежде всего, на калибровку интенсивности обслуживания устройств, в частности, для снижения простоев (в терминах теории СМО – уменьшения вероятности нахождения в состоянии, когда не заняты все или занята лишь малая часть обслуживающих устройств); для обеспечения перераспределения нагрузки между обслуживающими устройствами (более равномерного распределения вероятности нахождения системы в возможных состояниях).

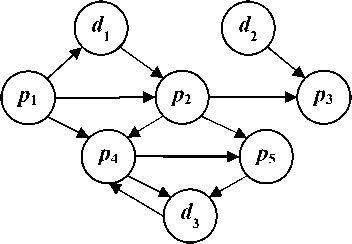
Рис. 4. Пример DFD-модели бизнес-процесса

Программная реализация

В исследовательском прототипе программной системы трансформации визуальных моделей бизнес-процессов реализованы следующие компоненты:

• 1)    компонент создания и обработки промежуточного представления графической модели бизнес-процесса (DFD-графа);

• 2)    компонент загрузки и обработки промежуточного представления модели в математический программный пакет Matlab.

При разработке компонента создания и обработки промежуточного представления графической модели бизнес-процесса использованы следующие инструментальные средства:

• 1)    интегрированная среда разработки (IDE) Microsoft Visual Studio 2012;

• 2)    средства языка программирования C# для обработки XML-файлов;

• 3)    CASE-средство автоматизированной разработки приложений CASEBERRY [1, 2, 5];

• 4)    средства технологии ASP.NET для разработки модуля доопределения модели.

При разработке компонента загрузки и обработки промежуточного представления модели в математический программный пакет Matlab использованы следующие средства:

• 1)    интегрированная   среда   разработки

(IDE) пакета Matlab;

• 2)    интегрированная среда разработки пользовательского интерфейса (GUIDE) Matlab;

• 3)    средства языка программирования Java для загрузки и обработки XML-файлов.

Заключение

Реализованный исследовательский прототип программной системы показал практическую значимость разработанного подхода. Открытая архитектура системы позволяет расширять функциональность за счет подключения новых программных компонентов, в которых, в частности, могут быть реализованы средства трансформации визуальных моделей в другие типы аналитических моделей для исследования различных аспектов реализации бизнес-процессов.

Для работы с визуальными моделями других типов могут быть использованы также средства трансформации моделей DSM-платформы MetaLanguage [6, 20].