О положительных решениях граничной задачи для нелинейного интегро-дифференциального уравнения на полубесконечном интервале

Рассмотрим следующую граничную задачу для нелинейного интегро-дифференциального уравнения первого порядка:

dE + д ^f K (т - t)h(t,E(t)) dt = 0, т е R⁺ := [0, +^),                              (1)

< т о

E(+ ro ) := lim Е(т ) = 0                                                            (2)

ч          т ^+f относительно искомой функции Е(т). Решение интегро-дифференциального уравнения (1) мы будем искать в следующем пространстве Соболева:

W1(R+) := {у : y(k) е Li(R+), к = 0,1}, где через у(к) обозыачеиа к-ая производная функции у.

В уравнении (1) д — положительный числовой параметр, а ядро K н нелинейность h удовлетворяют определенным условиям (см. ниже в формулировках основных теорем). Задача (1)—(2) возникает в кинетической теории плазмы (см. [1-3] и ссылки в них). В частности, задача (1)—(2) выводится из стационарного уравнения Больцмана и описывает стационарное распределение электронов в полубесконечной плазме, ограниченной плоскостью x = 0, при наличии чисто потенциального внешнего электрического поля. В уравнении (1) роль неизвестной функции E(x) играет первая координата электрического поля E(x) = (E(x), 0,0). Отметим, что задача (1)—(2) в линейном приближении достаточно подробно была исследована в работе [3]. В случае когда ядро K является вполне монотонной функцией и допускает определенное представление в виде суперпозиции экспонент при различных ограничениях на нелинейность h, задача (1)—(2) изучена в работах [4, 5].

В настоящей работе, при более слабых ограничениях на h и для общих консервативных ядер K, мы займемся построением однопараметрических семейств положительных решений в пространстве Соболева Wi1(R+). Будет изучено также асимптотическое поведение построенных решений в бесконечности в зависимости от значения свободного параметра, д.

В конце будут приведены частные примеры ядра K и нелинейности h, удовлетворяющие всем условиям доказанных теорем.

• 2.    Обозначения, вспомогательные факты и формулировка основных результатов

Пусть ядро K в уравнении (1) удовлетворяет следующим условиям:

• I)    K (x) > 0, x е R, K е L 1 (R) П C m (R), Jff K (x) dx = 1, где C m (R) — пространство непрерывных и ограниченных функций на R,

• II)    существует число a > 0 такое, что для всех а е (0, a)

  e αx

  
  

  ∞

  У K (t)dt

  
  

  е L i(R),

  
  

  x

  
  

• III)    характеристическое уравнение

∞

У K(t)(at — 1)e^atdt = 0

-∞ на интервале (0, а) имеет единственное решение, причем считается, что

∞ j \t\eatK(t)dt < +то.

-∞

Рассмотрим следующее семейство функций {Ta(x)}aG(o,a) :

Ta(x) := —e^ax

∞

У K (t) dt,

x Е R, a Е (0, a).

x

Из условия II) сразу следует, что T_a Е Li(R), a Е (0, a). Постараемся число a Е (0, а) выбрать так. чтобы

∞ bTahLi(R) := j \Ta(x)\ dx = 1.

-∞

В силу условия I) будем иметь

∞∞

µ

j e^axj K (.) dtdx=1.

-

∞

x

Используя теорему Фубини [6] с учетом I) и II) из (4), получим

∞

• ^— [ K(t)e^at dt = 1,    a Е (0,a).

  
  

α

-∞

Итак, для каждого параметра — >  0 мы должны найти число a Е (0, а) такое, что имело бы место соотношение (5).

С этой целью рассмотрим функцию

• —^(a) = —---^a------, ^{a Е (0,a)}-                           (^G)

J K (t)e^at dt

-∞

Заметим, что

—(+0) := lim —(a) = 0 a >0'

и

— t и а (0, ao ] 11 — ^ iia. [ao, a), где ao является единственным решением характеристического уравнения (3). Наибольшее значение функции —(a) равно rс КП antd, := — о- Итак, для a Е (0, а) имеет место ос ( )е

0 < —(a) ^ —о.                                       (7)

Обозначим через ai = ai(—) обратную функпню к <|>yiiKiiiiii —(a) на интервале (0, ao) и через a2 = a2(—) — обратную <|>ункнню к (функции —(a) на интервале (ao,a).

Зафиксируем числа аДц), ag и оДц) и относительно функции h предположим выполнение следующих условий:

• 1)    при каждом фиксированном значении t G R+ функция h(t,u) монотонно возраста от по и iiа. R+,

• 2)    (функция h(t,u) удовлетворяет условию Каратеодорп по аргументу ина множестве R+ х R+, т. е. при каждом (фиксированном и G R+ фушсиня h(t, и) измер! 1ма. по t п почти при всех t G R+ данная функпшi непрерывна по и на. R+,

• 3)    существует измеримая и неотрицательная функция e(t), определенная на R+, такая, что

  ∞

  
  

  e*(t) := e(t)e^a0t G L1(R⁺) П M (R⁺),

  
  

  т1(в*) := j 0

  
  

  te*(t) dt < +ro,

  
  

и функция h, удовлетворяющая следующему двойному неравенству:

и ^ h(t,и) <  и + e(t),   и G R⁺, t G R⁺.

Теперь мы готовы сформулировать основные результаты настоящей работы.

Справедливы следующие теоремы:

Теорема 1. Пусть ядро K и нелинейность h удовлетворяют условиям 1)-Ш) и 1)—3) соответственно. Тогда, при ц G (0, Цо) задача (1)—(2) в пространстве Соболева W₁¹(R⁺) обладает однопараметрическим семейством положительных решений {Ey(x)}yg(o,+^), причем для любого значения параметра y G (0, +то) имеет место следующее асимптотическое разложение для решения E y (x) :

E_y (x)e^ai(^^)x = y + o(1), x ^ +ro.

Теорема 2. При условиях I)—III), 1)—3), ec ли ц = цо, зад ача (1)—(2) в пространстве Соболева W1(R⁺) обладает также однопараметрическим семейством положительных решений {E_y (x)}Ye(o,+^), причем для любого y G (0, +то)

E_Y(x)e^a0x = yx + o(x), x ^ +ro.

ЗАМЕЧАНИЕ 1. Следует отметить, что в случае когда ц > Цо, вопрос существования положительных решений в пространстве W1(R⁺) для граничной задачи (1)-(2) до сих пор остается открытым.

• 3. Доказательство основных результатов

<1 Доказательство теоремы 1. Наряду с уравнением (1) рассмотрим следующие линейные однородные и неоднородные интегральные уравнения Винера — Хопфа:

∞

S(x) = j T_a(x — t)S(t) dt,  x ^ 0,

о

y(x)

∞

= g(x) + j T a (x

— t)^(t) dt,

x > 0,

относительно искомых функций S и ^ соответственно, где g(x) — неотрицательная ограниченная и суммируемая функция на [0, +то), причем

∞ mi(g) := У xg(x) dx <  + to .                           (11) о

Следуя обозначениям работы [7] через v(T_a) обозначим нервый момент ядра T_a :

∞ v(Ta) := У xTa(x) dx. -∞

Ниже убедимся, что v(T«1M) < 0, v (Tao )=0,

v(T«2M) > 0.

Действительно, из представления ядра T_a(x) в силу теоремы Фубини будем иметь

∞

∞

v (Ta) = Ц

xeαx

K (t) dt dx

-∞

x

∞t

=4K(t4

-∞   -∞

xe^a:x dx dt =

∞

[ K(t)(at — 1)e^at dt.

a2

-∞

С другой стороны, из (6) следует, что

∞

J K (t)(1 — at)e^at dt

^{Ц ( а )}

-∞

ОО                2

( J K (t)e^at dt\

a E (0, a).

Так как Ц (a₁) > 0, ц’(ао) = 0, ц‘(а₂) < 0 (см. §2), то из (15) сразу следует соотношения (12)—(14).

Из результатов работы [7], с учетом соотношений (12)—(13), немедленно следует, что

• А)    при a = а1(ц) уравнение (9) обладает положительным монотонно возрастающим непрерывным и ограниченным на R+ решением S*(x), а уравнение (10) суммируемым неотрицательным и ограниченным решением ^*(x);

• В)    при a = ao уравнение (9) обладает положительным монотонно возрастающим непрерывным и неограниченным на R+ решением S(x), причем S (x) имеет линейный рост S(x) = x + o(x), при x ^ +то, а уравнение (10) — ограниченным и неотрицательным решением <)5(x).

Рассмотрим теперь следующее вспомогательное нелинейное интегральное уравнение типа Гаммерштейна на полуоси:

∞

F (x) = yTM (x — t)e^aith(t,e^-a 1 tF (t)) dt,  x ^ 0,

о относительно искомой функции F(x), где

∞

Ta, (z) = ^e^a,Mz jK (t) dt, z e R, ai = аДд).                 (18)

z

Для уравнения (17) введем следующее семейство последовательных приближений: ∞

Fn_+i(x) = У Ta(х - t) e^a 1 th(t,^e-^a 1 tFn (t)) dt, x ^ 0,

0       *                                                               (19)

F0 ^ = SUDS'*Д) , n = ⁰, 1, 2, ■ ■ ■ , ^Y > °’ s Up S (x ) x>0

Индукцией no n сперва докажем, что при каждом y > °

Fn (x) t ^п° n                                  (20)

Действительно, учитывая условие 3), положительность ядра K, а также утверждение А), из (19) получим

∞

F1 (х) = j Ta i (х

- t)e^a 1 th t

e-ait YS *(t) sup S* (x) x>0

)

dt

∞

---Y— [ Ta, (x - t)S*(t) dt = -^^^У = f /(x).

sup S *(x)                           sup S *(x)     0

x>0        0                          x>0

Предположим теперь, что F„ (x) ^ FY-i(x) при пекотором n e N. Тогда с учетом монотонности функции h(t,u) (по u) и положительности ядра K из (19) будем иметь

∞

FY+i(x) >  j Ta, (x - t) e^ath(t,e^-atF_nLi(t)) dt = FY(x), 0

x > °, Y > °-

Теперь рассмотрим линейное неоднородное уравнение (10), в случае когда a = аДц) и

∞

g(x) = У T_a , (x — t)e^aite(t) dt, x > 0. 0

Очевидно, что g(x) ^ °, x ^ °. Убедимся теперь, что g e Li(R+) П M(R+), mi(g) < x.

Учитывая условие (4) и 3) из (21) для произвольного r > ° будем иметь

r

g(x) dx

r∞

У У Ta, (x — t) eaite(t) dt dx < r∞

У У Ta, (x — t)e*(t) dtdx

∞r

= У e*(t) У Tai (x

— t) dx dt

<

∞

У e*(t) dt < +x, 0

r

r∞

∞

r

У xg(x)dx ^ j x j Ta , (x - t)e*(t) dtdx = У e*(t) У T_a 1 (x — t)xdxdt

ибо

∞

r-t

∞

∞

∞

= I e*(t) У Ta, (y)(t + y) dydt ^ jt34td dt + j e*(f) dt I |y|Tai (y) dy< +~,

-t

-∞

∞

∞

∞

∞

t

j |y|Tai (y) dy = Д У |y|e^a1y Jk (t) dtdy = Д У K (t) У |y|e^a1y dy dt <  x.

-∞

-∞

y

-∞

-∞

(в силу того, что J—^ |t|e^a1tK(t) dt < +то). Устремляя r ^ +то, в последнем неравенстве приходим к следующим утверждениям:

g E Li(R⁺), mi(g) < +ro.

Ограниченность функции g нa R⁺ следует из оценки

∞

g(x) ^ sup e*(t) [ Tai (x t^0 J

— t) dt ^ sup e*(t) < +ro.

t>0

Теперь индукцией докажем, что

Fn^M< Д^ГТ ^⁽x)' sup S ( x ) x>0

x 3 0, y> 0, n = 0,1, 2,... ,

где у* является решением уравнеиия (10). в случае когда a = ai(p), а g(x) допускает представление (21).

При n = 0 неравенство (23) сразу следует из определения нулевого приближения и из неотрицательности функции y*(x). Предположим, что (23) имеет место при некотором натуральном п. Тогда, учитттвая условие 3), структуру (21) свободного члена g ii положительность ядра T_a1, из (19) будем иметь

∞

F,?+i(x) < Ca,(x — t)eaith t,e-ait    2ДтГ+ T*(t)    dt sup S (x)

0                     \         \ x>0                / /

<

∞

У Ta, (x — t)eait

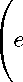
-α 1 t

YS*(t) sup S*(x) x>0

+ y*(t)   + e(t)   dt

γ sup S *(x) x>0

∞ j Ta, (x — t)S*(t) dt +

∞

У Ta, (x — t)y*(t) dt +

∞

У T_a, (x — t)e^a,te(t) dt

Y^S*^(x) sup S* (x) x>0

∞

+ [ Ta, (x — t)y*(t) dt + g(x)= ^yS 3x) + y*(x).

^,                           sup S^*(x)

0                                  x>0

Индукцией по n легко можно убедиться, что при всяком y > 0

FnY E C (R⁺),    n = 0,1,2,...

Действительно, непрерывность нулевого приближения сразу следует из непрерывности функции S*(x) (ем. утверждение А)). Если предполагать. что Fn (x) iienpepiявна по x при некотором n G N на. R⁺, то в силу непрерывности ядерной функции T_a 1 (x) ii a. R, свойств функции e(t) (см. условие 3)) н перавенства h(t, u) С u + e(t) u ^ 0. t ^ 0, из (19) следует непрерывность функции Fn^^) нa R⁺.

Таким образом, в силу (20) и (23) заключаем, что последовательность непрерывных функций {F„ (x)}^=o ПРИ каждом фиксированном y > 0 имеет поточечный предел, когда n→∞ lim FY(x) = FY(x), →∞ причем предельная функция удовлетворяет следующему двойному неравенству:

^YS ^(x)< FY(ir) < ^YS ^(x)__I- <р*(ж)    x 6 R⁺  7 > 0

supS*(x) c F (x) c supS*(x) + ^ (x),  x G R , Y > 0.

x>0                      x>0

Из непрерывности ядра T_a 1 нa R, свойств функции e(t) (см. условие 3)), неравенства h(t, u) С u + e(t)- u ^ 0. t ^ 0, ii опенки (25) сразу следует, что F ^Y G C (R⁺) при всяком Y > 0. И з ус.товия 2) в силу теоремы Б. Леви [С] следует, что при каждом y > 0 функция F ^Y(x) удовлетворяет уравнению (17).

Заметим теперь, что тогда функции вида

EY(x) := e

-

^a1^Mx f ^Y(x),   y > 0,

являются решениями уравнения

∞

E(x) = ц У T (x — t)h(t, E(t)) dt, x G R⁺, o

где

∞

T(z) := У K(t)dt, z G R.

z

Действительно, в силу непрерывности ядра K из (27) и (17) имеем

∞∞ ц У T(x — t)h(t,EY(t)) dt = ц У T(x — t)h(t,e

∞

-

^а1 ⁽^t F ^Y (t)) dt

= e^-a1⁽^^)x у Ta 1 (x — t)e^a1 ^Wh(t, e

-

^a 1 ⁽^ F ^Y (t)) dt = e

-

^а1 ⁽^^)xF ^Y(x) = E y (x),    y> 0.

o

Так как K G Li(R) П C m (R), to из (28) следует, что существует

T ‘(x) = — K (x) G Li(R) П C m (R).

С другой стороны, в силу неравенства h(t, u) С u + e(t), u ^ 0, t > 0, и условия 1) имеем ∞∞ ц j |T‘(x — t)|h(t, Ey(t)) dt С Ц j K(x — t)(EY(t) + e(t)) dt

∞

С ц У K (x — t) o

e ^a 1 tF ^y (t) dt + цs_Up e(t) c ц(sup F ^Y(x) + supв(х)) < +^,

t^o

x^0

x>0

∞∞

(JT ^,(x ^—

∞∞

t)|h(t,E_Y(t))dtdx ^ У У K (x

— t)(e ^a 1 tF ^Y(t) + e(t)) dtdx

∞    ∞    ∞∞

^ j e ^a tF ^Y(t) У K(y)dydt + У e(t) У K(x — t) dxdt ^

0           -∞            0     0

sup F ^Y (x) x>0

α 1

∞

+у e(t)

dt < +ro.

Следовательно, согласно теореме о дифференцировании под знаком интеграла (см. [8]), можем утверждать, что функции Ey € W11(R⁺), Y > 0, и удовлетворяют граничной задаче (1)—(2).

Заметим теперь, что задаваемая посредством формулы (21) функция g(x) обладает также следующим свойством:

lim g(x) = 0.                                      (29)

Действительно, так как в* € Li(R+) П M(R+), a Ta1 € Li(R) П Cm(R), из [9, лемма 5] следует, что limx ,. ^ g(x) = 0. Используя [9, лемма 5], соотношение (29) и тот факт, что у* € L1(R+) П M(R+), из (10) (при a = а1(ц)) получаем, что liin  y*(x) = 0.

Учитывая (29), (30), (25) и тот факт, что S*(x) f supS*(x), когда x ^ +то, можем x>0

утверждать, что Ey (x)e^a 1 x = y + o(1)- ^к°^гД^а x ^ + to. >

• <1 ДОКАЗАТЕЛЬСТВО теоремы 2. Для доказательства теоремы 2 нам понадобятся результаты пункта В) для уравнений (9) и (10) при a = ao. Доказательство осуществляется аналогичными рассуждениями с единственным исключением: вместо вспомогательного уравнения (17) рассматривается нелинейное интегральное уравнение вида

∞

• F (x) = у Ta₀ (x — t)e^a0th(t, e^-ao tF (t)) dt, x € R⁺,                 (31)

и вместо последовательных приближений (19) здесь берутся следующие итерации:

∞

Fn₊₁(x) = У Ta₀(x — t)e^aoth(t,e-^ao tFn(t))dt, x € R⁺ 0

F0(x) = YS(x), n = 0,1, 2,... , y > 0, где S(x) является решением однородного линейного интегрального уравнения (9) при a = ao (см. утверледение В)). >

ЗАМЕЧАНИЕ 2. Рассмотрим следующий частный пример: K(x) = 2 e^-|x|, x € R. Тогда характеристическое уравнение (3) принимает вид:

3a2 — 1 = 0, a € (0,1)

(a € (0,1) для выполиепня условии II)).

В данном случае ao = ^13 € (0,1), а функция ^(a) допускает следующее представле ние

[1(a) — a(1 — a^), a € (0,1).

Заметим, что д f 11г i ^0, —3) ид ^ 11a. (—3, 1) , причем до = д(ао) = 3—3.

В этом случае первый момент ядра Т_а допускает следующее преставление:

V (Та) =

д(3а2 — 1)

a2(1 — a)2(1 + a)2 '

где цe-(1-a)x,               x ^ o, цeax(1 — ex) + цeax, x < 0.

Та(х) = |

Ниже, в частном случае, когда

K (x) =

2 e

^|x|,   x G R, h(t, u) = u,

приведем явный вид решения граничной задачи (1)—(2).

Громоздкие, но простые вычисления показывают, что при д = до = 3—3

E(x) = c1xe V3x + c2e Vsx, x g R+, а при д < до = 3—3 решение задачи (1)—(2) допускает следующее представление

x

где

E(x) = c1e

+ C2e

A

2 x,

A = —= cos Va

(

aVa

- arccos---- д a2

.

Следует отметить, что при д > до мы получаем знакопеременные решения, которые не имеют физического смысла.

Заметим, что в случае д G ^0, 3^^) полученные функции удовлетворяют граничной задаче (1)-(2), если ci = — 1-^) С2, где

A а1(д) = —

-

Д2Н1Е, а2(д) = A

.

В том случае, когда д = до = 3^, конетанты ci и С2 должны удовлетворять соотношению c2 = VT ci"

Следовательно, в данном случае однопараметрическим семейством положительных и ограниченных решений служат функции:

• ^{а)    лр}”^{д G} (⁰- з5з) -

  E y (x) = Y (V^a1^Mx

  
  

  _-

  
  
  
  

  _-

  
  

  _-

  
  

  а2(д) а1(д)^е

  
  

  -

  
  

  ^а2^(ц)х) ,   x G R⁺, Y > 0,

  
  

• ^ь)    ИР” ^д = Л,

  E_y (x) = Ye

  
  

  √x3

  
  

  x+

  
  

  V3

  
  

  V3

  
  

  —1

  
  

  ^,

  
  

  Y > 0, x G R⁺

  
  

• 4.    Примеры ядра K и нелинейности h

Заметим также, что в этом случае, когда р ^ +0, число A ^ 1, а решение E^(x), при каждом фиксированном x G R+, стремится к Y, ибо ai(+0) = 0, a2(+0) = 1.

В приложениях часто встречаются следующие ядерные функции K [1-3]:

• I)    K (x) = 2 e^-|x|. x G R,

• II)    K (x) = ^f е^-1^ ds. x G R,

1 s

III) K (x) =

t= e 4a. a >  0. x G R. 4na

Легко можно убедиться, что для выше приведенных ядерных функций K выполняются все условия доказанных теорем. Подробно остановимся на функции III). В этом случае функция р(а) допускает следующее представление:

р(а) = ае =а2, а > 0, и ее точка максимума ад = ^2=. Кроме того, рд = ^ и ад = ai(p) является обратной функцией функции р(а) на интервале ^0, ^2=) •

Приведем также несколько примеров нелинейности h(t, u) и функции e(t):

• a)    h(t, u) = ^u(u + e(t))■ u ^ 0. t ^ 0,

• b)    h(t, u) = u + uu+l)• u ^ 0. t ^ 0,

• c)    h(t, u) = u 1 + U+. c > 0. u >  0. t >  0,

Ei) e(t) = e-l2. t G R+, e2) e(t) = e—(ao+$)1. t G R+. ж > 0, — параметр.

E₃) e(t) = te^-2a 0 t. t G R⁺.

Отметим, что для примеров а)-с) выполнение условий 1)—3) можно доказать прямой проверкой.