О порогах кавитации в высоковязкой ньютоновской жидкости при воздействии коротких импульсов

В работе [6] было получено аналитическое выражение для определения порога кавитации в высоковязкой жидкости на основании анализа уравнения Нолтинга - Непайраса для сферического пузырька [4,7-9]. Это уравнение было принято в виде [6]:

RR + 3 R2 + — - 1 (Ро — Рр +—) (—)3У + — R =Z0,      (1)Z

2     pR р V 0   rp   R0J\rJ     pR      0,

-1(Po-Pp-sin(^t)) ,(2)

где t - время, R - текущий радиус пузырька, R_o - начальный радиус пузырька, о - поверхностное натяжение, Р_о - гидростатическое давление, со = 2л/' - круговая частота, f - частота возбуждения.

Для случая воздействия прямоугольных импульсов растяжения и сжатия длительностью: T/2 , где T=2π/ω [6]:

^—^Р о —Р р —Р т ),          (3)

при условии, что время расширения пузырька: т < Т/2.

По оценкам, проведенным в работе [6, 417 c], критическая длительность импульса т_ст = pR²/n и соответственно частоты - f_CT = p/2pR² . где R -характерный размер радиуса пузырька при расширении пузырька [6]. Для глицерина при значениях R =500 мкм, f_CT = 25 кГц, f < f_CT и вязкий член больше инерционного [6].

Время расширения пузырька не будет превосходить T/2 при условии [6]:

R

Р т >Р о -Р р + ^fln — ,  (4)

где Р_т - амплитуда давления.

Аналитическое выражение для порога кавитации в вязком режиме Р ^ примет вид [6]:

R

P^P o — P p + Spfln- ,       (5)

Неравенство (4) будет справедливо и при значениях радиуса меньших характерного радиуса R , что справедливо и для максимального радиуса при расширении пузырька R_m . Используя условие (4) определим зависимость отношения R_m/R₀ от амплитуды давления:

Р т =Р о — Р р +8??fln -= ,       (6)

^к 0

И выражение для отношения:

Rm/R0 = exp^-^)       (7)

В работе [6] не было приведено сопоставления результатов расчета порога по аналитическому выражению (5) с результатами численных расчетов уравнения Нолтинга - Непайраса. Поэтому практический интерес представляет сравнение значений порогов кавитации, полученных по выражению (5) и значений отношения Rm/R0 (7) с соответствующими значениями, полученными при численных расчетах уравнения Нолтинга - Непайраса [4] и уравнения Флинна [3].

В уравнении Флинна для расчета пульсаций кавитационного пузырька, используется учет сжимаемости в первом приближении, при условии, что скорость движения жидкости вне пузырька - и_г меньше скорости звука - с₀: u_T/c_Q « 1.

В предлагаемой работе уравнение Флинна принято в виде:

p[r (1—iR) r+2 (1—_lr) R2] = (1+т^['(R) — '"I+ Д1 -^'(R)                       (8)

Давление на бесконечности при синусоидальном давлении [7-9] Р ^ = Р₀ —

Р_т51п()У Давление на поверхности пузырька:

P(R) = Р — 2^ —4^^^ , 9   R    R dt давление газа внутри пузырька с поправкой, следующей из закона Ван дер

Ваальса [10-11 ]:

^Р 9 = (^Р О ⁺^⁽ТШ,                        (9)

где, h = R 0 , а =8,54 для воздуха и 8,86 для аргона [10-11].

Если обозначить правую часть уравнения (8) - Qd (инерционные члены), а вязкий член - Q^ = ~~, то при значении их отношения Qr = ^ > 0,5 как показано ниже, реализуется коллапс пузырька.

Как показывают расчеты, учет сжимаемости в уравнении Флинна [3] позволяет более точно определять числа Маха в жидкости при сжатии пузырька, чем уравнение Релея - Плессета, которое точно описывает поведение газа внутри пузырька [10,11].

Сопоставление численных решений уравнения Флинна [3] с результатами численных решений уравнения Кирквуда - Бете - Джилмора [7-9], проведенное в [12] показало совпадение результатов расчетов пульсаций пузырьков в вязкой жидкости для ряда моделированных функцией Хевисайда импульсов давления. Следует отметить, что в [12] второй член в правой части уравнения Флинна приведен со знаком «-» вместо знака «+».

Выражение для давления на бесконечности:  Р» = Р0 — P(t) в случае би полярных прямоугольных импульсов примет вид [12]:

Р » =P o -P_mSH,                                 (10)

где SH = H(t) — 2H (t — | ) + H(t — Т) для биполярного импульса [12], H - функция Хевисайда. Как известно, функция Хевисайда относится к обобщенным функциям, дифференцируема и используется в моделировании сигналов различной физической природы [13]. Сопоставление результатов численных расчетов пульсаций пузырьков при воздействии импульсов, моделированных функцией Хевисайда, с численными расчетами и экспериментальными данными однопузырьковой сонолюминесценции приведено в тестовых примерах [12] .

Начальные условия при: t=0, "~^ = = 0, ^(0) = R 0 (11).

Как видно из рис.1 a,b в обоих случаях пузырек расширяется за полпериода t=T/2 (25 мкс ), но в фазе сжатия в случае биполярного импульса при t=T радиус пузырька R(T) <  R₀, а под действием однополярного импульса при t=T, R(T) >  R₀, и следовательно эффективность трансформации энергии, запасенной пузырьком за время его расширения, снижается за счет более длительной фазы сжатия t>T/2 .

a b

Рис. 1аб. Расширение и сжатие кавитационного пузырька в глицерине (выделено голубым цветом). a) под действием биполярного и b) однополярного коротких импульсов (выделены красным цветом). у = 4/3

Проведенные расчеты с использованием численных решений для слабых ультразвуковых полей <  2 бар показало, что значения отношения R_m/R₀ < 2,5 в этом случае слишком малы для возникновения кавитации в глицерине и в его растворах (95^99%) (табл.1).

Таблица 1. Вязкость глицерина и зависимость отношения радиусов пузырька R_m / R_o от вязкости п и концентрации глицерина в водном растворе при амплитуде Р_т = 2 бара, температуре t = 20 o C , f = 20 кГц [14 ].

C% вес	100	99	98	97	96	95
п Pa • c	1,49	1,194	0,971	0,802	0,659	0,543
ρ кг/м³	1261	1259	1257	1254	1252	1249
R m/ R o	1,62	1,76	1,91	2,0	2,34	2,54

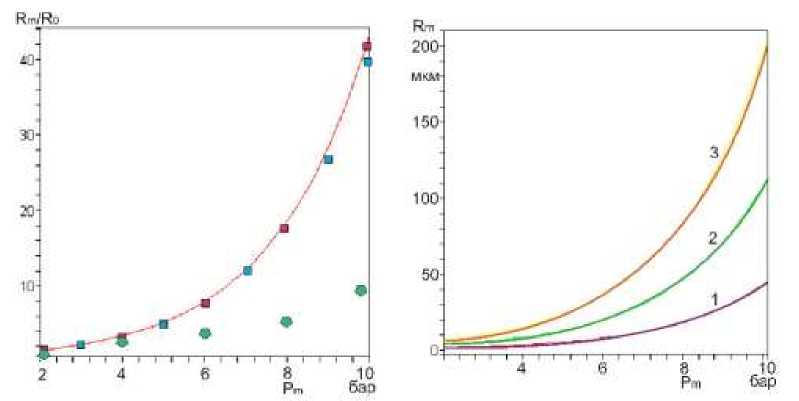
На рис.2а,Ь приведены результаты расчета значений отношения R_m/R₀ и порогов кавитации в глицерине, полученных по аналитическому выражению (7) и численных решений уравнения (8). Значения свойств: η=1,49, с=5,49• 10^-2 Н/м, у =1. Как видно из рисунка 2 a,b значения отношения R / R , определенных по формуле (7) и полученных при численном решении уравнений (1,8) для случая чистого глицерина п = 1,49 Pa • ^с и прямоугольных импульсов

a

b

Рис.2а,Ь а). Зависимость отношения - R _m / R_o от амплитуды давления - P <  10 бар.

Сплошная кривая рассчитана по формуле (7). Квадратами обозначены результаты численного расчета уравнения Нолтинга - Непайраса и уравнения Флинна для прямоугольных импульсов, многоугольниками – для случая синусоидальных импульсов.

b) Зависимость максимального радиуса - R от амплитуды давления - P по вы- ражению (7) - кривые 1, 2, 3 при величине Ro = 1,4,5, 10мкм соответственно.

в интервале умеренных ультразвуковых полей 2-10 бар совпадают с с точностью графического выполнения рис.2a. Для случая синусоидальных импульсов расхождения нарастают при превышении амплитуды р > 4 бар, а при амплитуде р > 10 бар величина Rm / Ro меньше в три раза. чем для случая прямоугольных импульсов (рис.2b). Это означает, что выражение (7) применимо только для случая прямоугольных импульсов.

Для определения порога кавитации в работе [6] использовалась характерная величина R% = 500 мкм , имеющая смысл критического радиуса.

Значение критического радиуса можно уточнить, если использовать известное из литературы выражение для критического радиуса пузырька, расширяющегося в высоковязкой жидкости:

Rcr = (3Ш)  [-1 + 1 + _42!^Ц        (12)

^CT \ 3у 7 Ро [      \     (-y-l^pj           ^{v 7}

Для глицерина при значениях параметров (табл.1) R_CT = 265 мкм.

Выражение для порога кавитации, полученное с учетом поправки (9), в данной работе имеет вид :

D3-h3 ^Y

P        '     :          .                        (13)

В фазе расширения пузырька при у=1, в выражении (13) R = R_CT .

a

b

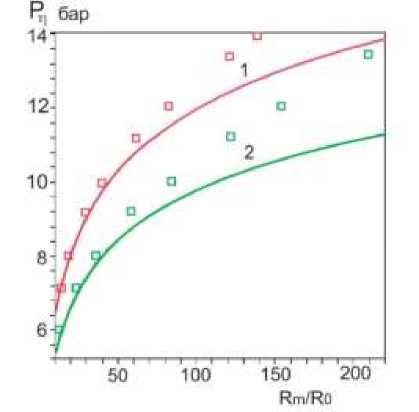
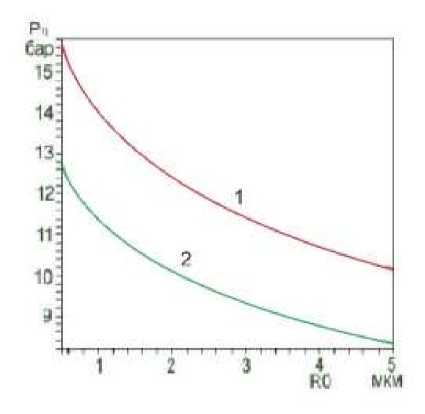
Рис.3 Пороги кавитации в глицерине для случая прямоугольных импульсов.

• а)    Кривые -1, 2 рассчитаны выражению (13), кривая 1- при значении вязкости п = 1,49 , кривая 2 при вязкости п = 1,194 Pa • c , результаты численных расчетов по уравнению (5) при у = 1 обозначены квадратами.

• b)    зависимость порогов кавитации от начального радиуса в пределах 0,5 –5 мкм, рассчитанные по выражению (13) кривая 1 п = 1.49 кривая 2 п = 1.194 Pa • c .

Анализ результатов (Рис. 3 a,b) показывает, что при снижении концентрации глицерина в водном растворе всего на 1% относительно исходной величины вязкости падение величины порога кавитации может составить 20–25%.

Величина порога кавитации также сильно падает с ростом начального радиуса пузырька (Рис. 3b). При увеличении значения начального радиуса на по- рядок падение величины порога кавитации составляет ~ 25%.

Дифференциальный критерий коллапса пузырька в вязкой ньютоновской жидкости был получен при аналитическом решении модифицированного уравнение Релея в форме [1]:

к^1 + -(^2 + dt:2    2\dt:/

4д dR

~   - ~

R dt

= 0 ,

с безразмерными переменными:

n            1

-------, a =    - 1 , p R o U 0       8%

R = R , % = tU o , д

R о        R о при начальных условиях [1 ]:  R%%= 0} = 1, —{%= 0} = -1

dt %

Условие коллапса кавитационного пузырька для случая гидростатического давления [1]: / %«1   и вязкого демпфирования / % > 1 ,

Для поля переменного давления коллапс пузырька скими значениями дифференциального критерия [1]:

определяется критиче-

%) = ( —

-R ( t ) p R ( t )

-t 8n ’

(16),

с текущими значениями в

фазе сжатия пузырька

% ) <- 1 и расширения

%) >  1 .

Текущие значения критерия

U p R ( t )                     U p R ( t )

<% t ) ^ ——— и величины Jee =       , изменя-

8n                           n ются в соответствии с пульсациями пузырька и зависят от давления, начального радиуса пузырька и вязкости, как параметров, а при фиксированном значении вязкости и начального радиуса определяются амплитудой давления Pm [1]. Их компоненты, соотношение и размерность находятся в том же соответствии, что и в гидродинамическом числе Рейнольдса - R = — —

, где U и L характерные величины скорости и размера потока соответ ственно. Закон подобия

Рейнольдса в вязкой несжимаемой жидкости определяет подобие течений, обтекающих геометрически подобные тела в отсутствии свободных поверхностей [15]. Текущие значения величин Re(t) и c(t) позволяют оценивать динамику отдельного пузырька и сравнивать динамику пузырьков разного радиуса в процессе их расширения и сжатия в вязкой ньютоновской жидкости. В связи с этим последовательность чисел этих величин, характеризую- щая динамику пузырька, можно назвать текущими значениями чисел Рейнольдса Re(t) для случая динамики пузырьков.

Величина дифференциального критерия может быть рассчитана при известной амплитуде давления - Рт при численном решении уравнения динамики пузырька [1]. Задача данной работы – определение амплитуды порогового давления Ртк = Рл  при условии c(t) > 1 и c(t) < — 1 для ряда значений начального радиуса R0. С этой целью использовался метод моделирования функцией Хевисайда последовательности прямоугольных импульсов с изменяющейся амплитудой [12]. Ниже будет показано, что при определении порога кавитации можно ограничиться положительным значением величины: c(t) = 1. Импульсы давления должны быть разнесены по оси времени. (Термин ортогональные сигналы или импульсы не используется, поскольку в рассматриваемых случаях их последовательность не обязательно организует линейное метрическое пространство [12,13]). Выражение для последовательности биполярных прямоугольных импульсов давления с паузами между ними т = T /2 и нарастанием амплитуды давления, задаваемой рациональной аналитической функцией, в данном случае по экспоненте [12]: n+1

Ps( t) = PK Z SHi( t)            (17), i=1

где SH = H ( t - т + т ) - 2 H ( t - T + T ) + H ( t - T + т ) , n - число коротких импульсов в последовательности импульсов, т = i (T + T ) , i -текущий индекс, T -длительность короткого импульса, т -величина паузы между короткими импульсами, т = T + т , т = т + т • т = т + т • k = exp( t / Ф ) Ф - величина, задающая степень нарастания амплитуды импульсов. В конкретном случае (рис. 4a,b) T = 50 мкс, т_р = 0.5 T , ф = 0.001 . Выражение для давления на бесконечности для этого случая: р = P _o - р ( t ) . Рис. 4-5 иллюстрируют принцип использования предлагаемого метода на основе численного решения уравнения Флинна (8).

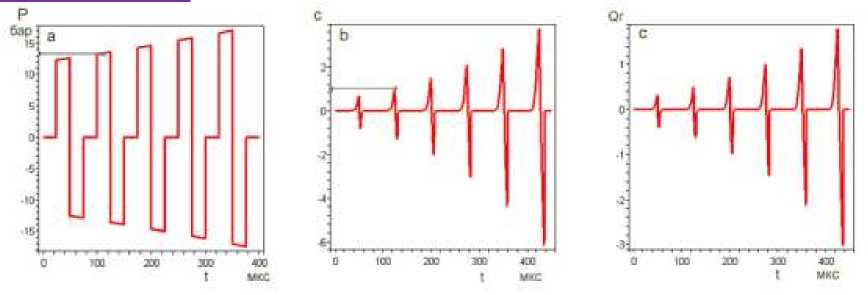
Рис.4 a,b.c. Определение порога кавитации P по критерию <%= 1 при длительности им пульса T = 50 мкс и паузе т = T /2, Ro = 1 мкм а) зависимость давления P от времени, b)

зависимость критерия С от времени, с) зависимость отношения Qx = Qd / Q — от време- ни.

В момент максимального расширения пузырька на втором импульсе при давлении Ртк = Р^ = 13,3 бара, величина отношения Qr = 0,5 , дифференциальный критерий принимает значение с (t) =1. В момент мак симального сжатия значение c(t) = -1,2 рис. 4 а,Ь,с Такие соотношения, как правило, соблюдается при определении порога Р^ в рассматриваемом интервале T=0.5–50 мкс.

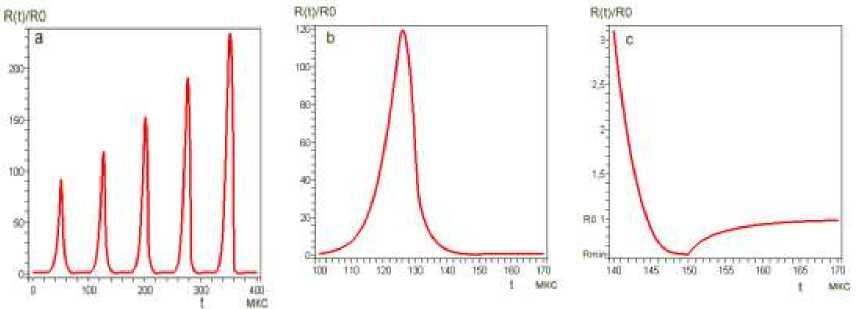
Рис 5 a,b,с. a) Зависимость отношения значений радиусов R(t) / R от времени. b) зависимость отношения R(t) / R для 2-ого импульса, с) определение минимального радиуса Rjп = R /6.

Использование критерия c(t) и величины Re позволяет получить зависимость величины - Р^ от длительности импульса T при численных расчетах уравнения (8). Величина порога кавитации в жидкости растет с уменьшением длительности импульса при воздействии коротких импульсов [16]. Результаты расчетов, проведенных в предлагаемой работе для глицерина, показали увеличение порога кавитации на порядок при сокращении длительности прямоугольного импульса от T=50 мкс до значения 5 мкс.

При разрушении жидкости зависимость порогового давления от длительности импульса [16] :

Р“Т = const,        (18)

для глицерина [16]:

РТ = const

Выражение (19) соответствует экспериментальным данным для микросе-кундного диапазона [16].

Аналитическое выражение Р - (Т), в интервале 30-50 мкс для прямо угольных биполярных импульсов, примет вид:

Р„ = Ро - Р„ + ^-InT^I-T3)       (19)

^-     0     ^р зт   С^-т³)

Следует отметить, что согласно выражению (20) при фиксированных значениях вязкости п и длительности T порог Р - уменьшается с увеличением начального радиуса R₀.

Анализ и сопоставление результатов численных расчетов по уравнению Флинна и аналитическому выражению (19) - показывает удовлетворительное соответствие результатов при значениях длительности импульсов в интервале 30-50 мкс , что определяется допущениями работы [6]. Наибольшие расхождения приходятся на интервал 0,5-2 мкс .

В этой связи практический интерес представляют упрощенные оценки порога кавитации Р - в более широких пределах 0,5-50 мкс при сокращении количества численных вычислений уравнения динамики пузырька. Модифицированное аналитическое выражение на основе (19) имеет вид:

Р , = P s (j) "                (20)

где t - длительность импульса, Ps - величина порогового давления при значении t=1 мкс, ks =1 мкс (для соблюдения размерности) , n -для уточнения зависимости порога Р^ от начального радиуса R0 . и формы импульса.

Ниже приведены примеры оценок порога Р ^ по выражению (20) для случая прямоугольных и синусоидальных импульсов при значениях радиуса R₀ = 1, 10 мкм и R₀=1, 5 мкм соответственно. Для прямоугольных импульсов рис. 8a:

R₀ = 1 мкм, P_s = 440 бар, п = 0,9; R₀ = 10 мкм, P _s = 180 бар, п = 0,78;

Для синусоидальных импульсов рис.8b;

R₀ = 1 мкм, P _s = 665 бар, п = 0.87;    R₀ = 5 мкм, P _s = 382 бар, п = 0.81;

Рис. 6. Зависимость порога кавитации P от длительности импульса t , в пределах 0,5–50 мкс, кривые - результаты расчета по аналитическому выражению (20), точками обозначены результаты численного решения. a) прямоугольные импульсы, кривая 1:

R0 = 1 мкм, кривая 2 - 10 мкм b) синусоидальные импульсы, кривая 1: R0 = 1, кривая 2: -5

мкм. c) пороги кавитации длительности t в пределах 0,5–5 мкс: кривая 1 – синусоидальные короткие импульсы, кривая 2 –прямоугольные.

Выражение для последовательности коротких синусоидальных импульсов с паузами т_р = Т /2 (при т_р = 4Т ke положительно) имеет вид [12]:

n

SH = £ SHi( t)     (21), i=1

ограничимся простым случаем n = 4 : SH = SH + SH + SH + SH , где

SH = - ke ( H ( t - т ) — H ( t — T )) sin( to t ) SH ₂ = ke ( H ( t - т ) — H ( t - T )) sin( to t ) SH₃ = - ke ( H ( t - т ) - H ( t - т )) sin( to t ) SH ₄ = ke ( H ( t - т ) - H ( t - т ))) sin( to t )

4 = тp = T/2, т2 = тх + T , т3 = т2 + тp, т4 = т3 + T далее аналогично.

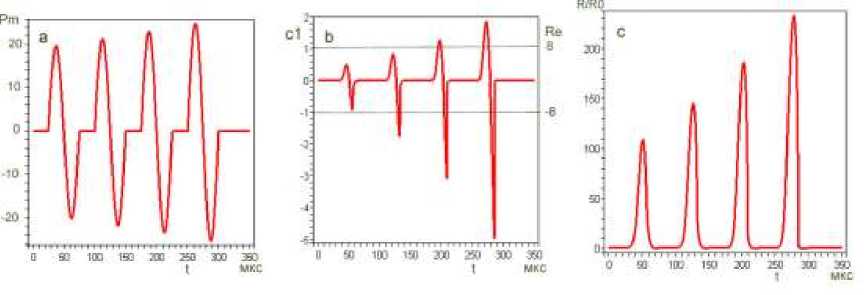
Рис. 7. Определение порога кавитации по критерию - c % и величине

при длительности синусоидальных импульсов T = 50 мкс и тр = T /2 а) Зависимость амплитуды давления от времени b) зависимость критерия С% от времени с) зависимость отношения R(t)/ R от времени. (На рис.7Ь обозначение с - с1).

Величина порога для синусоидальных импульсов в данном случае при значении с = 1 (на третьем импульсе) составляет Р ^ =22,5 бара, это больше порога кавитации для прямоугольных импульсов в 1,7

раза. Величина паузы должна увеличиваться с сокращением длительности импульса рис.8. На рис. 8 а,с величина паузы - тр = 4Т , порог кавитации

Р ^ = 665 бар при значении с = 1 на первом импульсе.

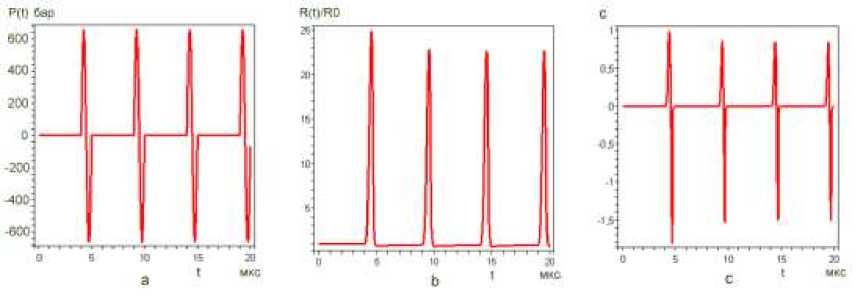
Рис. 8 Определение порога кавитации при воздействии короткого синусоидального импульса длительностью t =1 мкс.

Рис 9 a,b,c. a) Зависимость давления от времени в коротком импульсе из четырех колебаний без паузы при T= 1 мкс, b) Затухание колебаний - падение величины R (t)/R ₀ с) зависимость дифференциального критерия коллапса от времени.

Падение амплитуды колебаний – величины максимального радиуса пузырька - Rm при постоянной амплитуде переменного давления и фиксированных величин T=1 мкс, R0 = 1 мкм можно объяснить тем, что система в отсутствии пауз между колебаниями не успевает возвратиться в равновесное состояние. А поскольку движущая сила продолжает действовать, то сдвиговые явления в вязкой жидкости могут нарастать, и падение амплитуды уже со второго импульса при указанных фиксированных параметрах и свойствах полностью определяется вязкостью. Подобное явление было предсказано и объяснено исходя из гидродинамики в работе [17] .

При сравнении результатов данной работы с результатами ряда экспериментальных и теоретических работ [18-22] применительно к вязким жидкостям и в частности к глицерину, необходимо учитывать, что определение порога кавитации по дифференциальному критерию коллапса предполагает наличие в ограниченном объеме вязкой жидкости микроскопических пузырьков. а экспериментальное измерение давления разрыва жидкости в большинстве работ предполагает идеально однородную жидкость. В такой жидкости при экспериментальном измерении критических растягивающих давлений (напряжений) жидкости – TS наиболее часто предполагается гомогенное зарождение новой фазы в виде сферических зародышей, либо по механизму откола в твердом теле в виде поры [18-22]. С учетом этого следует ограничиться только сопоставлением порядка величин пороговых давлений и рассматривать эти сопоставления, как качественные оценки.

Величина измеренной датчиком величины TS в глицерине при расчетном интервале радиуса возникших из зародышей и растущих по вязкому закону пузырьков (0,01-10) мкм составила 250 бар [19]. В данной работе порог кавитации для пузырьков R₀ = 10 мкм случае прямоугольных импульсов составлял 300 бар, а в случае синусоидальных 440 бар при длительности импульса T=0,5 мкс.

При снижении температуры глицерина от 350 ° K до 220 ° K под действием импульсов 0,1-0,4 мкс величина TS однородно изменялось от 0,34 до 2,5 кбара, а при температуре ниже 220 ° K разрушение глицерина предположительно происходило по механизму откола (crack) [20]. Если принять линейную зависимость давления разрыва от температуры в указанном интервале, то при 293° K величина TS=1190 бар, а порог кавитации при радиусе R₀ = 1 мкм в случае синусоидальных импульсов 1200 бар – прямоугольных импульсов 840 бар. Эти оценки следует рассматривать как оценки на качественном уровне.

С увеличением объема жидкости возрастает вероятность гетерогенного образования кавитационных зародышей, поэтому в ряде экспериментальных работ измерение TS производят в пленках и микроканалах (microfluidics) [23]. Динамический разрыв глицерина и D.I. воды в микроканалах (dynamic rupture in microfluidics), реализованный при воздействии короткого импуль- са длительностью 7 наносекунд от мощного IK лазера, происходил с расширением возникшего сферического пузырька в интервале 30-50 мкм и распространением сферических ударных волн с давлением до 3500 бар. При этом у пузырька сохранялась сферическая форма вплоть до встречи с отраженной от свободной поверхности волной. Величина напряжения разрыва для глицерина составила – TS = 617 бар (61,7 мПа) [23].