О постановке граничных условий при решении задач гидродинамики в переменных завихренность - функция тока

Теории постановки граничного условия для завихренности посвящен ряд фундаментальных работ [1–3], существенный прогресс в данном направлении был достигнут в работе [4], где был установлен коэффициент аппроксимационной формулы для завихренности, оптимизирующий скорость сходимости численной процедуры с использованием такой формулы. Следующим шагом построения теории было доказательство того, что существующие различные способы и процедуры определения завихренности на стенке при решении уравнений завихренность – функция тока эквивалентны между собой [5] и сводятся к использованию аппроксимационной формулы общего вида. Это позволяет устранить различия в разностных схемах уравнений завихренность – функция тока, связанные со способом определения завихренности на стенке. Однако все данные подходы основаны на идее использования ряда Тейлора a i = 1, e i = 1 или его модификаций a i = 1, e i = 1 для функции тока

Ф(П) = Ф(h) + «(п - в1 h)^ + «2'^ + аз   / О + -’ дп         2    д'2         6 д'

в котором первая и вторая производные заменялись на функцию граничной скорости и завихренности соответственно. Здесь η – нормальная к границе координата, h - шаг дискретной схемы. Количество членов ряда и коэффициенты ( a i , e i ) определялись различными исследователями [1–4] в зависимости от точности получаемого дискретного аналога задачи. Однако изложенный здесь подход создания промежуточных граничных условий, несмотря на достигнутые значимые успехи, имеет два серьезных недостатка. Во-первых, он требует построения основанного на ряде Тейлора дискретного аналога, ортогонального границе в каждом граничном узле расчетной области, что существенно усложняет алгоритмы для задач с криволинейными границами. Во-вторых, он порождает дополнительный итерационный процесс даже для линейной задачи Стокса.

Использование метода конечных элементов для решения рассматриваемой задачи позволяет [6] избавиться от первого недостатка. Использование при решении задачи итерационных методов [7–9], позволяет переместить процесс вычисления промежуточных граничных условий в основной итерационный процесс, т. е. частично компенсировать второй недостаток, но не избавиться от него.

Ниже рассмотрен алгоритм, реализующий альтернативный подход формирования граничных условий для завихренности, который можно реализовать при решении задач в формулировке завихренность – функция тока при использовании метода конечных элементов.

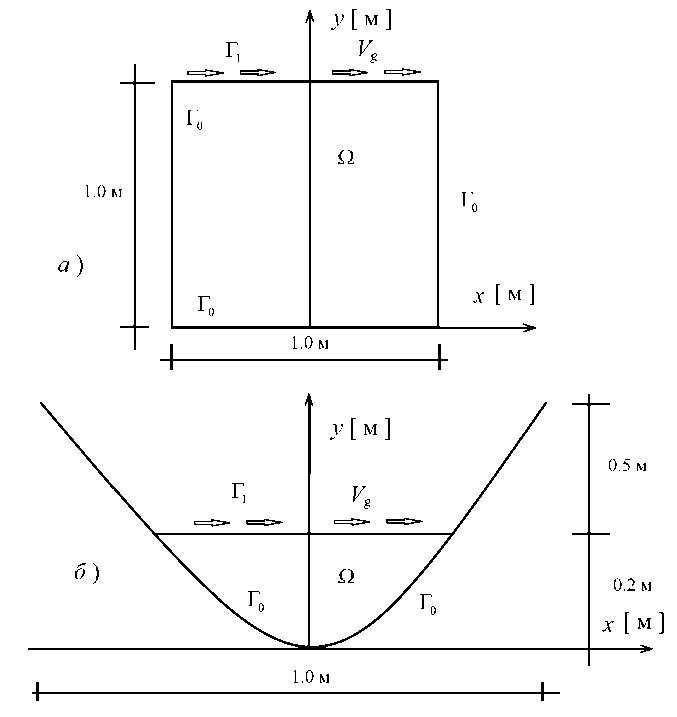
Рис. 1 . Геометрии расчетной области Q и их границ Г = Г 0 U Г 1 для прямоугольной каверны (а) и параболической каверны (б)

1. Постановка задачи

Рассмотрим вынужденное конвективное течение вязкой жидкости в полости с подвижной крышкой (каверне). Схемы геометрии расчетной области Q, ее границ приведены на рис. 1. Известные уравнения Навье – Стокса в переменных скорость– давление описывают движения вязкой жидкости и имеют вид dV  dp _ (d2 V  d2V \ dW  dp _ /

^ρ dt   ∂x ^µ ∂x ²    ∂y ^{2   , ρ} dt   ∂y ^µ

∂ ² W ∂x ²

∂ ² W

+        ,

dv +dW ^{= 0} , (1) ∂x ∂y

где ρ – плотность жидкости, µ – вязкость жидкости, V и W – компоненты скорости потока в декартовых координатах (x, y ), p - давление, t - время. Уравнения (1) замыкаются начальными условиями

V _0, W _ 0, (x, у) е Q (2) и граничными условиями V _0, W _ 0, (x, у) е Г0, (3) V _ Vg , W _ 0, (x, у) е Г1, (4) здесь Vg – скорость движения крышки.

Выберем новые переменные - функцию тока Ф и завихренность ш , определенные следующим образом через компоненты скорости V и W :

V _ ^, W _ ∂y

дФ

∂x .

Из определения Ф и ш следует д 2 Ф д 2 Ф

ax2 ⁺ аУ ^{2 ш _ _0} -

Из уравнений движения (1) с помощью перекрестного дифференцирования (первого уравнения (1) – по y, второго уравнения (1) – по x) и их последующего вычитания исключается давление p и получается уравнение переноса завихренности dω

г* ^{_ д}

/ д ² ш д ² ш \

∂x ² ∂y ^{2 .}

Переход от уравнений постановки задачи в естественных переменных (1) – (4) к постановке в переменных функция тока Ф и завихренность ш требует для уравнений (6), (7) постановки граничных условий для переменных ш, Ф. Преобразование условий (2) – (4) с использованием зависимостей (5) позволяет получить начальные ш _ 0,   (x, у) е Q

и граничные условия дФ      дФ

— _ 0, - _ 0,

∂y      ∂x

д Ф

(x, у ) е ^г о > gy ^{_ v} g >

д Ф

7- ^{_ 0} ,    ^{( x}, У ) ^е Г 1 ,

∂x

к которым добавляется условие нулевого потока через границу Г области

Ф _ 0,   (x, у) е Г.

Отметим, что граничные условия (9), (10) являются переопределенными для функции тока Ф и отсутствуют для завихренности ш . Перед переходом к процессу обсуждения граничных условий для завихренности сформулируем вспомогательную задачу

Стокса, которая содержит в себе линейное стационарное уравнение для завихренности и уравнение (6) для функции тока:

д²ш д ² ш

∂x ²    ∂y ²

д ² Ф д ² Ф    _

∂x ²    ∂y ²

Поскольку для уравнений (11), (12) задачи Стокса требуются граничные условия, аналогичные задаче Навье – Стокса (6), (7), то на них будет более удобно демонстрировать предлагаемый в работе подход по их реализации.

2. Слабая формулировка для задачи Стокса

Используем для общности получаемых дискретных конечно-элементных аналогов SUPG-метод [10], который будет избыточен при решении задачи (8) – (12), но необходим при решении задачи (6) – (10). Введем интерполяцию сеточных искомых функций Ф ^- , u h на конечном элементе

Ф ^- = N e Ф е , u h = N e u _s ,    в = 1, N.

где Ф д , ш в — узловые значения функций, N e — функции формы N p Е L 2 , N _k - количество узлов на конечном элементе. Используя весовые функции N _α ∈ L ₂ , получим слабую формулировку задачи Стока в дискретной области Q ^h :

[ ( N ^ + ^^ d_a - f N a Пха¥ + ny^) dr,     (14)

_Ω h    ∂x ∂x ∂y ∂y          _Γ h         ∂x ∂y

/ (

Ω ^h

3N_a д Ф ^h ∂x ∂x

+ д^дФ^) d^= / N_au^hd Q+ ! N_a(n _x d5 h + X y дФ^] dr, (15) ∂y ∂y          _Ω h             _Γ h         ∂x ∂y

где ( n _x , n y ) - компоненты вектора нормали к границе r ^h . Поскольку на границе области r ^h значение завихренности будет ш ^h определено, поверхностный интеграл в тождестве (14) можно приравнять к нулю [6, 11]. Учитывая граничные условия (9), (10) для функции тока Ф ^h , преобразуем (15) к виду

Ω h

8N_a дФ ^h ∂x ∂x

+ ГТ^Г-^ dQ = / N_au ^h dQ + [ NV g d r .

∂y ∂y           _Ω h              _{Γ 1}h

С учетом (13) получим алгебраический аналог задачи

K αβ

L0

-

M αβ

K αβ

] [ У - И ’

где K _α β – матрица жесткости, M _α β – матрица масс, Q _α – правая часть конечноэлементного дискретного аналога

К ав -[ (NTN^ + ^дГ^дТ^е) d Q , M ae -[ NN e d Q , Q a = [ N_aV g dT.

_Ω h    ∂x ∂x ∂y ∂y                  _Ω h                     _{Γ 1}h

Выполним сборку глобальной матрицы жесткости A ij и правой части F i для задачи Стокса, получив систему

A j X j - F i , i,j -0,..,N,                          (18)

где А -и FCa 0 1 [Kae -Mae 1 [j 0 1 Aj =Ue [ о CaJ [ о   Kae J [ о j ■ x-u 'C 0 Ж1 f-u R 0 1 [Qa1 Xj = Ue [ 0 Ciy [швJ ’ Fi = Ue [ 0 Ce,] [ 0 здесь Ue (*) — оператор сборки локальных дискретных аналогов в глобальную систему алгебраических уравнений задачи, Cieα – матрица кинематических связей для e-го конечного элемента, определяемая типом конечного элемента [11] и свойствами сеточной области Qh. Отметим, что система (18) учитывает граничные условия Неймана (9). Следовательно, если бы нам были известны все значения функции тока Фе в узлах расчетной сетки, из уравнений (16) мы смогли бы восстановить все узловые значения завихренности ωβ. Однако выполнение граничных условий Дирихле (10) для функции тока Фi на границе области rh приводит к потере в системе (18) информации о данных связях в граничных узлах. Основная идея работы заключается в сохранении данной информации и ее использовании для предотвращения вырождения системы (17) при выполнении граничных условий для функции тока. Потерянную информацию о данных связях в граничных узлах задачи (xi, yi) Е Г1 можно восстановить, используя слабую формулировку (15):

U e C f_a M De C je C ee ^ в = U e C ea^ j C ee Ф в — U f C fa Q a ,

^M α ^D β

=/

Ωh

N _a N^^std Q ,

для функции завихренности ω _i в каждом i -м граничном узле определяем тождество (19) с кусочно-постоянной функцией формы N eons = 1 для конечных элементов, дающих ненулевой вклад в i граничный узел. Использование выражения (19) для всех значений завихренности u i на границе области r h позволяет заменить условия Дирихле для функции завихренности ω i на границе с условием Неймана, которые в методе конечных элементов выполняются ≪ естественным ≫ образом [11]. Недостатком такого подхода является необходимость построения для каждого узлового значения ω _i на r h дискретных аналогов (19) отличающихся от (16) матрицами масс M _ae = M De • Однако выполненные численные исследования показали, что выполнение простых алгебраических операций над системой (18) позволяет достичь результата, аналогичного применению тождества (19). Для достижения данной цели выполним ряд операций над системой (18). Отметим, что для каждого узла дискретной области в системе (18) определены два уравнения. Для каждого граничного узла системы (18) приведем строку U e C f_a M _ae C ee первого уравнения к диагональному виду путем построчного суммирования компонент строки с установлением полученной суммы на главную диагональ матрицы U e C f_a M _ae C ee , совершив таким образом неявное преобразование U e C f_a M _ae C ee в U e C fa M De C jee • Полученным уравнением заменяется связное с граничным узлом уравнение для завихренности, неявно выполняя таким образом условие (19). После выполнения такой операции для всех граничных узлов в этих узлах производится выполнение граничного условия Дирихле (10) для функции тока. Отметим, что данный алгоритм без изменений может применяться при решении задачи Навье – Стокса (6) – (10) и легко модифицируется для решения других задач, например, при решении задач Навье – Стокса с потоком массы через границу области. В этом случае изменится только правая часть системы (18) на этапе выполнения условия Дирихле (10). Достоинством предлагаемого метода является отсутствие двух недостатков, указанных во введении, т. е. в необходимости создания промежуточных граничных условий [4, 5] и в построении на криволинейных границах [2, 3, 8, 9] дополнительных дифференциальных операторов, ортогональных контуру границы.

Несмотря на двукратное увеличение размера матрицы (18), практика ее решения показывает, что сходимость по нелинейности задачи на каждом шаге по времени существенно выше, чем при последовательном решении задач [7]. Точность восстановления значения функции завихренности ω в данном способе определения граничных условий в целом зависит от порядка и вида используемого конечного элемента, вида интерполяционных и весовых функций формы. И хотя точность граничного условия ω непосредственно связана с интерполяционными характеристиками конечного элемента, требуются дополнительные исследования для элементов высокого порядка по влиянию операции перехода от распределенной к диагональной матрицы масс при модификации уравнений (19).

3. Дискретный аналог для стационарной задачиНавье – Стокса

Используем метод конечных элементов в формулировке Петрова – Галеркина. Разобьем расчетную область Q на трехузловые конечные элементы Q e , Q h = U e Q e . Введем на конечном элементе функции формы [11] N α :

N _a = a _a + b _a x + c _a y

и их частные производные

∂Nα      ∂Nα ba     q ,   ca     q

∂x        ∂y коэффициенты которых выражаются как

<	x 2 y 3 - x 3 y 2		y 2 - y 3	x 3 - x 2
a 1 =	2S     ’	Ь 1 =	2S ’	c 1 =	2S
	x 3 y 1 - x 1 y 3		y 3 - y 1		x 1 - x 3
a 2 =	2S     ’	b 2 =	2S ’	c 2 =	2S
	x 1 y 2 - x 2 y 1		y 1 - y 2		x 2 - x 1
a 3 =	2S     ’	Ь з =	2S ’	C 3 =	2S

Г1 X 1 У 1

S = 1 X 2 У 2

L1 Х з Уз.

где x _k , y _k – координаты вершин (узлов) конечного элемента, S – площадь конечного элемента. Определим аппроксимацию искомых функций на конечном элементе

Ф ^h = N e Ф е , U h = N e и в ,    в = M,                    (22)

где Ф в , и в , V e , W e — значения искомых полей в узлах конечного элемента. Для противопоточной стабилизации дискретного аналога задачи воспользуемся методом Петрова – Галеркина (SUPG) [10] с весовыми функциями L _α ∈ H ₂ ¹ :

L a    N a + a^{h ( A} x b a + A y c a ),

где Ax = —       ^{a a}      =, Ay =-- ^{a a} =, h = 0, 5 ^ S, 0 <  a <  1.

У ( b a Ф a ) 2 + (C a Ф a ) ²             ^a) + (C a Ф a ) 2

Используя интерполяцию (20) – (23), преобразуем интегральные тождества слабой формулировки для уравнения Навье – Стокса

[ /dN a дФ ^h

_Ω h ∂x ∂x

dN _a dФ ^h ∂y ∂y

) dQ + / N a U ^h d Q + f N a V g dr = 0, Ω ^h                  Γ ₁ ^h

_{Ω h}   ρL α

dФ ^h du ^h ∂y ∂x

-

дФ ^ ^du h \ +   ( dL a du h

∂x ∂y µ ∂x ∂x

+"L dH d"

∂y ∂y

в дискретный аналог задачи

^{— К} ав

M αβ ^р C aeY ^ Y + ^рК ав

здесь

S Г 2 11

К ав = ( Ь а Ь в + С а С в ) S, М ав =     1 2 1

12 1 1 2

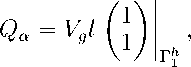
C aeY = ^{( Е} а + ^{ah (} A x b a + A y ^c a ))( c Y ^Ь в - b^Yc e ^{) S}, ^E a = ^{(1 /}3, 1/3, V³), где K _αβ – матрица жесткости/диффузии, C _αβ_γ – матрица конвекции, M _αβ – матрица масс, Q α – правая часть конечно-элементного дискретного аналога, l – длина граничного конечного элемента. Отметим, что метод сборки глобальной системы алгебраических уравнений из дискретного аналога для задачи Навье – Стокса (24) и предложенный способ выполнения граничных условий для функции завихренности одинаков с задачей Стокса, рассмотренной в разделе 3. Для восстановления поля скорости по формуле (5) на конечном элементе по узловым значениям функции тока определялись значения компонент скорости

Ve = СаФа,  We = -ba Фа, которые далее методом линейной интерполяции разносились в узлы расчетной области Qh.

• 4.    Результаты расчетов

Ниже приведены результаты расчетов, которые подтверждают эффективность предложенного метода удовлетворения граничного условия для завихренности при решении задач вынужденной конвекции в случае стационарной постановки (6) – (10).

Верификация расчетов была произведена путем сравнения с результатами других авторов для расчетной области Q h , представленной на рис. 1 а). Рассмотрим конвективное движение жидкости в прямоугольной каверне со сторонами 1 м. Горизонтальное движение верхней границы каверны происходит с постоянной скоростью V g = 1 м/с.

Жидкость в каверне имеет постоянную по области вязкость, величина которой определяется вариантом задачи и может принимать значение 1: ^ = 10 ; 2: ^ = 1 ; 3: ^ = 5/16 кг/мс. Соответственно, числа Рейнольдса для получаемых решений имеют следующие значения Re = 1: 100, 2: 1000, 3: 3200 и согласуются с работами [1, 3]. Расчеты для данной расчетной области выполнялись на сетках 125 x 125. На рис. 2 в качестве демонстрации выполненных расчетов приведено поле модуля скорости полученное для Re = 1000. На рис. 2 также приведены вертикальная линий 1 и горизонтальная линия 2, проходящие через геометрический центр каверны. Вдоль этих линий будет выполняться сравнение полученных расчетных данных с результатами других авторов. На рис. 3, 4 сплошными кривыми 1 приведены скорости для V вдоль вертикальных линий y (рис. 2, линия 1) и скорости W вдоль горизонтальных линий x (рис. 2, линия 2).

Нулевые оси этих графиков для различных значений Re были смещены для наглядности профилей. Из этих профилей видно, что с увеличением числа Рейнольдса происходит истончение пограничных слоев стенки, хотя скорость этого истончения невелика из-за малого диапазона изменения числа Re.

Пунктирными кривыми 2 на рис. 3 и рис. 4 представлены результаты вычислений, выполненных в работе [12] на сетках 129 x 129 скалярными разностными схемами

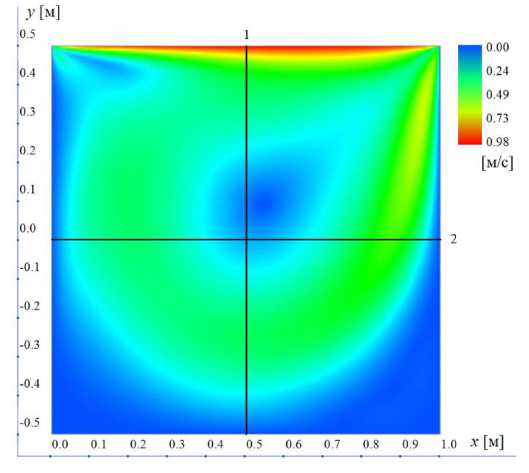
Рис. 2 . Модуль поля скорости, полученный в расчета при Re=1000; 1, 2 – вертикальная и горизонтальная линии, проходящие через геометрический центр каверны

3-го порядка. Для скорости V точечными множествами на рис. 3 приведены результаты, полученные Агарвалом [1] c помощью точных разностных схем третьего порядка на сетках 121 x 121. Для скорости W точечными множествами на рис. 4 приведены результаты, полученные Налласами и К.К. Прасадом в работе [12].

Из сравнения полученных результатов видно, что, несмотря на третий порядок разностных схем, использованных в работах [1] и [12], и первый порядок интерполяции, использованный в данной работе, полученные результаты хорошо согласуются с решениями, опубликованными в работах [1] и [12].

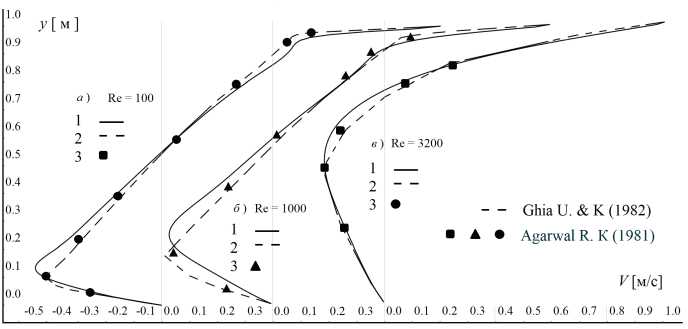
Рис. 3 . Сравнение горизонтальных скоростей V вдоль вертикальной линии, проходящей через геометрический центр каверны для различных чисел Рейнольдса

В качестве демонстрации применимости предложенного алгоритма по выполнению граничного условия для поля завихренности, при решении задач в расчетных областях, имеющих сложную геометрическую форму, рассмотрим полученные результаты для расчетной области Ω , геометрия которой представлена на рис. 1 (б). Вынужденное конвективное движение жидкости в каверне с параболическим дном задается горизонтальным движением верхней границы каверны Γ 1 , с постоянной скоростью V _g = 0,1 м/с.

Жидкость в каверне имеет постоянную по области Ω вязкость, величина которой определяется вариантом задачи и может принимать значения 1: µ = 0, 2 ; 2: µ = 0, 02 ;

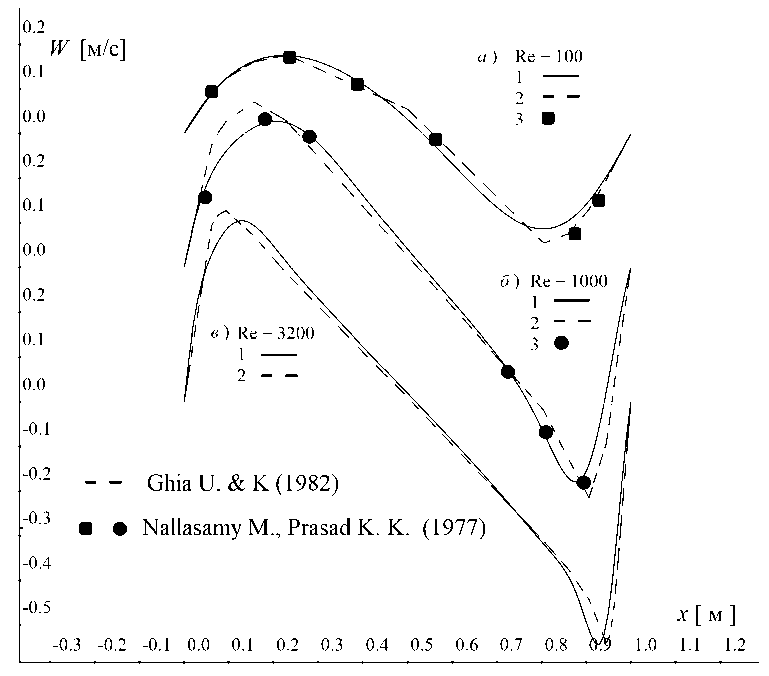
Рис. 4 . Сравнение вертикальных скоростей W вдоль горизонтальной линии, проходящей через геометрический центр каверны для различных чисел Рейнольдса

• 3:    µ = 0, 00625 кг/мс. Соответственно, числа Рейнольдса для получаемых решений имеют следующие значения Re = 1: 100, 2: 1000, 3: 3200. Расчеты для данной расчетной области выполнялись на нерегулярных сетках в 15000 узлов.

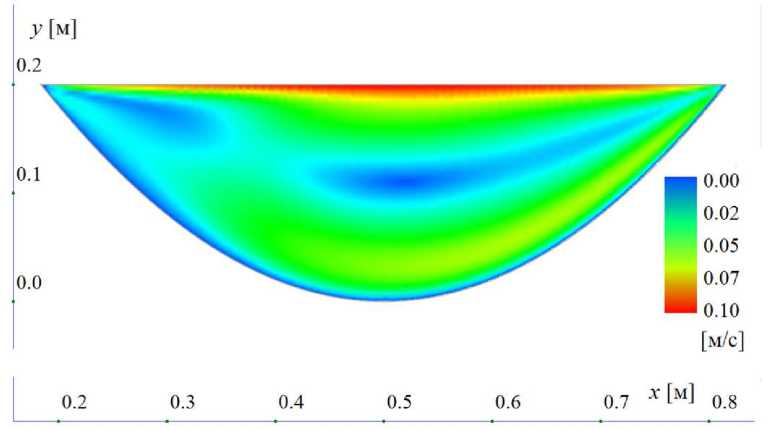
Рис. 5 . Модуль поля скорости, полученный в расчета при Re = 1000

На рис. 5 в качестве демонстрации выполненных расчетов приведено поле модуля скорости, полученное для Re = 1000. На рис. 6 кривыми 1–3 приведены скорости для V для различных значений числа Re вдоль вертикальной линии y , расположенной на оси симметрии каверны. Поскольку для данной расчетной области (являющейся прототипом створа речного канала) отсутствуют данные, сторонние для сравнения, нулевые оси этих графиков не смещались. Изменение профилей при увеличении числа Рейнольдса происходит аналогично изменениям, описанным для первой задачи.

Однако в отличие от первой задачи получить установившийся профиль скорости для Re = 3200 (рис. 6, кривая 3) не удалось из-за образовавшегося в левом углу области пульсирующего вихря. На рис. 6 это выражается в том, что значение вычисленной скорости V на границе не согласуется с граничной скоростью V _g . При этом профиль скорости (кривая 3) постоянно изменяется при итерациях по нелинейности/(псевдо–

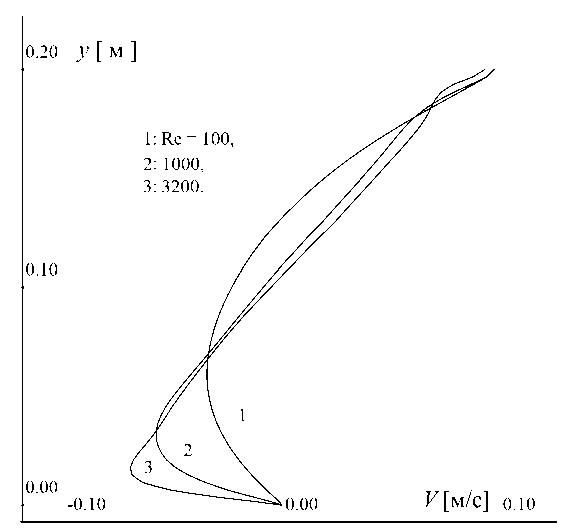
Рис. 6. Горизонтальные скорости V вдоль вертикальной линии y , проходящей через геометрический центр параболической каверны, для различных чисел Рейнольдса времени), однако максимальные наблюдаемые изменения в пограничных слоях потока не превышают 15 % от скорости крышки Vg . Из полученных результатов было сделано предположение, что для заданной геометрии расчетной области (рис. 1 б)) при числах Re = 3200 не существует стационарного решения задачи.

Заключение

Проведенная апробация алгоритма по выполнению граничного условия для завихренности при решении задачи Навье – Стокса (6) – (10) показывает его надежность и эффективность. Перспективным является развитие данного подхода для получения граничных условий для задач с более сложной геометрией, например при анализе вторичных потоков в створах рек.

Исследование выполнено за счет средств гранта Российского научного фонда № 24-17-20009 и гранта Правительства Хабаровского края (соглашение № 108С/2024 от 31.07.2024 г.) .