О построении математической модели грузового автомобиля «Урал» с колесной формулой 4 x 4

Общеизвестно [1], что наибольшая средняя скорость движения автомобиля при передвижении по пересеченной местности зависит, главным образом, от того, насколько удачно при проектировании автомобиля подобраны и реализованы

• 1)    технико-экономические параметры моторно-трансмиссионных агрегатов;

• 2)    конструкция, технические параметры и характеристики подвески.

Как правило, в конструкциях современных автомобилей первая из отмеченных двух задач решается достаточно успешно, и мы, в дальнейшем, будем считать, что она, «априори», решена. Это, по мнению многих ведущих ученых (Г.О. Котиев, Е.Б. Сарач [1], В .А. Савочкин, А.А. Дмитриев [2] и др.), всегда можно обеспечить, например, за счет увеличения мощности силового агрегата. Что же касается реализации второй задачи, то здесь необходимо иметь в виду, что до настоящего времени ещё не предложено достаточно эффективного, конструктивного метода её решения. В связи с изложенным, остановимся на обсуждении предлагаемого нами направления решения именно второй задачи.

Предварительно отметим, что оптимизация конструкции, параметров и технических характеристик подвески позволяет не только существенно увеличить среднюю скорость движения автомобиля по пересеченной местности, но и повысить плавность хода, комфортабельность движения автомобиля, снизить динамические нагрузки на узлы, агрегаты автомобиля, на пассажиров и перевозимый груз.

Общеизвестно также [1], что наилучшие показатели быстроходности, управляемости, устойчивости и безопасности движения транспортного средства, при условии ограниченности динамических нагрузок на узлы, агрегаты автомобиля, на пассажиров и перевозимый груз, могут быть достигнуты при использовании в подвеске упругих элементов с нелинейной характеристикой и адаптивных амортизаторов.

При этом непременно предполагается, что при проектировании упругих элементов и адаптивных амортизаторов осуществлены оптимальный подбор и согласование их рабочих характеристик и реализован оптимальный алгоритм управления адаптивным амортизатором. А данная задача может быть решена на основе использования достаточно точной математической модели автомобиля.

В настоящей работе в качестве объекта исследования рассматривается грузовой автомобиль «Урал» с колесной формулой 4x4, предназначенный для движения по изношенным дорогам и бездорожью. Обладая высокой проходимостью, этот автомобиль, к сожалению, имеет низкую плавность хода, а также относительно невысокую среднюю скорость движения по пересеченной местности. Для устранения данных недостатков нами были разработаны конструкции упругих элементов с нелинейной характеристикой и адаптивные амортизаторы пассивного типа. Однако эффективное использование их в конструкции автомобиля «Урал» предполагает предварительное создание математической модели автомобиля, учитывающей специфические рабочие характеристики этих новых элементов подвески. Остановимся на обсуждении основных особенностей построения математической модели.

Традиционно используемая математическая модель автомобиля [3] учитывает два вида возмущающего воздействия на автомобиль: со стороны дорожного полотна и со стороны силового агрегата. Оба источника возмущений замыкаются на колесе автомобиля и передают кинематическое и силовое воздействие на колебательную систему подрессоренных и неподрессоренных частей автомобиля.

Внешнее возмущающее воздействие со стороны дорожного полотна, обусловленное наличием неровностей дороги, наиболее неблагоприятным образом проявляется при резонансном режиме движения на дороге с прямыми волнами синусоидального профиля, описываемой в работе Н.Н. Яценко [4]. Условия движения будут определяться высотой неровностей, их длиной и скоростью движения автомобиля, которую примем постоянной. Имея в виду известную из теории подвески автомобиля зависимость между скоростью автомобиля, длиной неровностей и частотой возмущающей силы, условия движения можно выразить только частотой возмущения и высотой неровностей. Тогда внешнее воздействие на рассматриваемую нами колебательную систему может быть выражено аналитически выражением

q ( t ) = q ( t )_max ⋅ (1 - cos ω t ),                                                                                (1)

где q ( t ) – внешнее воздействие; q ( t ) max –амплитуда внешнего воздействия; ω – частота внешнего воздействия.

При существующей базе автомобиля, равной 4,4 м, принимаем из условия максимальной интенсивности внешнего воздействия максимальную высоту неровности равной 7 см, а длину неровности равной 2 м. Принятые размеры неровности значительно превышают размер пятна контакта колеса с опорной поверхностью. Поэтому допустимо принять точечный контакт колеса с опорной поверхностью.

На основании вышеизложенного будем исследовать движение «плоской» модели автомобиля с нелинейными характеристиками подвески по синусоидальным периодическим неровностям и по единичным неровностям. Это позволит проанализировать наиболее тяжелые условия движения автомобиля.

Функциональная модель автомобиля представляет собой «плоскую» многомассовую динамическую систему, состоящую из двух подсистем:

• –    подсистема «дорога – колеса – неподрессоренная часть – подрессоренная часть – кабина – водитель на сиденье» (рис. 1), отражающая вертикальные и продольно-угловые колебания подрессоренных и неподрессоренных масс на подвесках;

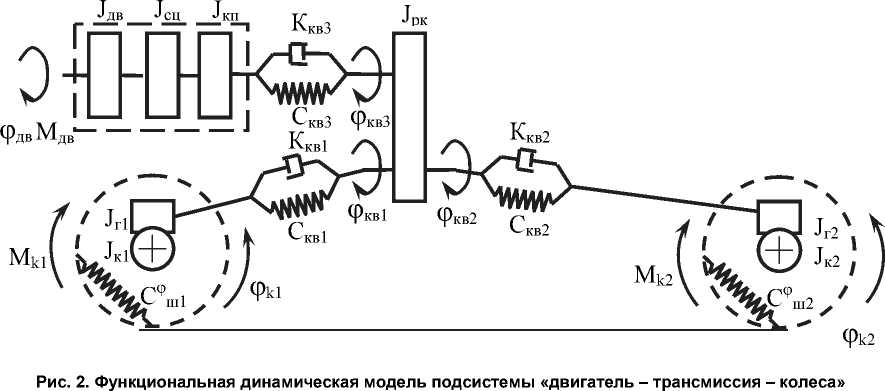
• –    подсистема «двигатель – трансмиссия – колеса» (рис. 2), отражающая угловые колебания элементов трансмиссии и колес.

При этом представленные подсистемы связаны между собой через ведущие колеса и реакции на колесах, что определяет взаимосвязь нелинейных угловых колебаний трансмиссии и подрессоренных масс.

Подсистема «дорога – колеса – неподрессоренная часть – подрессоренная часть – кабина – водитель на сиденье»

Функциональная модель содержит следующие элементы подрессоривания и упругодиссипативные связи:

• 1)    внешнее воздействие со стороны неровностей дороги;

• 2)    неподрессоренная часть (мосты, колеса, ½ часть подвесок и карданных валов) на шинах;

• 3)    подрессоренная часть на рессорных подвесках с амортизаторами;

• 4)    кабина на пружинных подвесках с амортизаторами;

• 5)    водитель на подрессоренном сиденье.

Подсистема «двигатель – трансмиссия – колеса»

При переезде неровностей на ведущих колесах автомобиля возникают тангенсальные реакции, которые, в свою очередь, вызывают угловые колебания в трансмиссии. В связи с этим в функциональной модели автомобиля учитываются следующие динамические элементы трансмиссии.

• 1)    Внешнее воздействие со стороны крутящего момента двигателя.

• 2)    Моменты инерции агрегатов трансмиссии (двигатель, сцепление, коробка передач, раздаточная коробка, карданные валы, главная передача, полуоси, колеса), приведенные к наиболее податливым участкам.

• 3)    Угловые жесткости и демпфирование наиболее податливых участков трансмиссии.

Расчет и конструирование

z20 A z30 A

J п М п

J каб М каб М с

Θ 30

x 3

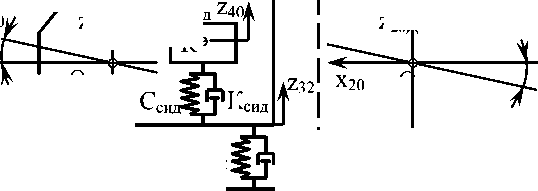
R®

К

Θ 20

О каб

К к2 L

С к1

К к1

М п2

К п2

V

М п1

ξ п2

С п2

С п1

К п1

/ хп2

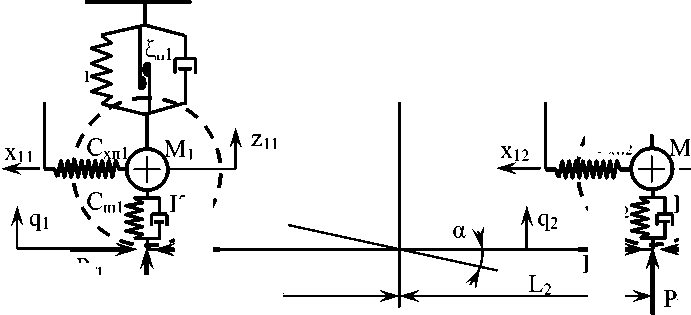
ξ п1

К ш1/

2 1 I К ш2 !

'Сш2

Р f2

N2

Р f1

Р N1

Р k1     L ₁

Рис. 1. Функциональная динамическая модель подсистемы «дорога – колеса – неподрессоренная часть – подрессоренная часть – кабина – водитель на сиденье»

Р k2

Наиболее значимые элементы подвески характеризуются нелинейными характеристиками. Упругие свойства шины описываются радиальной и тангенциальной упругими характеристиками, которые определены с учетом потерь на внутреннее трение. Аналогично описываются упругие характеристики подвески автомобиля (передняя и задняя) в вертикальном направлении, учитывающие сухое трение в рессорах, а также упругая характеристика сиденья водителя (пассажира). Кроме того, нелинейными характеристиками описываются амортизаторы подвески.

Следует иметь в виду, что при достаточно точном описании упруго-диссипативных элементов подвески соответствующие рабочие характеристики отображаются функциями переменной структуры, которые «сшиваются» из отдельных участков. В связи с этим на графиках первой и второй производной, к которым относятся исследуемые параметры скорости и ускорения эле- ментов подрессоривания, появляются разрывы первого и второго рода. Данное обстоятельство приводит к качественному искажению динамического портрета колебательной системы. Для устранения подобного «дефекта» динамической системы предлагается метод преобразования динамических систем переменной структуры в динамические системы постоянной структуры, базирующийся на использовании функции у = arctg (x) [5]. С помощью этого метода все нелинейные характеристики подвески аппроксимировались непрерывными функциями постоянной структуры. Для примера рассмотрим радиальную упругую характеристику шины (рис. 3).

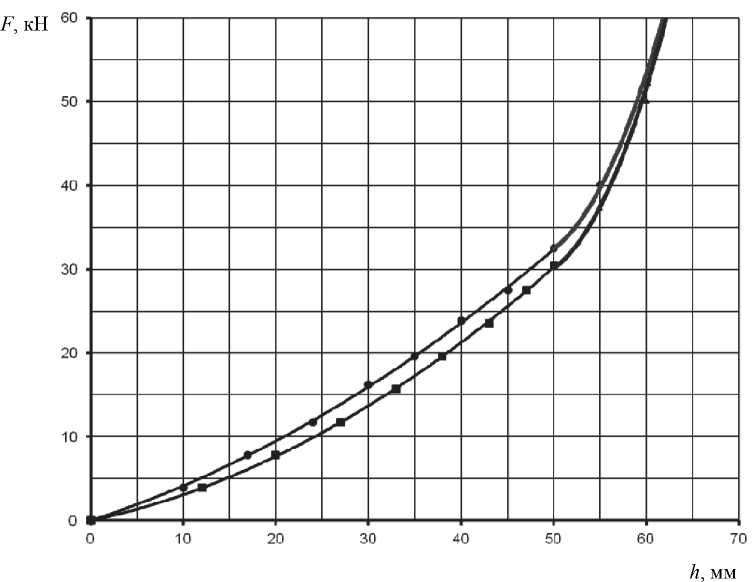
Рис. 3. Радиальная упругая характеристика шины

Упругая характеристика состоит из двух функций: F _н( h ) - функция нагрузки, F _р( h ) - функция разгрузки. Данные функции имеют две общие точки (начальную и конечную) и образуют петлю гистерезиса.

Функции нагрузки и разгрузки, являющиеся функциями переменной структуры, имеют, соответственно, следующий вид:

F ( h ) =

'0,0058 h ² + 0,3591 h ;

^ 0,1315 h ² - 12 , 37 h + 322,34;

V h e [0;50[;

V h e [50; 70];

F _p ( h ) = [ 0,0074 h ² + 0,2353 h ;

0,1387 h ² - 13,108 h + 338 , 61;

V h e [0;50[;

V h e [50; 70].

Воспользовавшись упомянутым выше методом, представим выражения (2) и (3) в виде следующих, уже непрерывных на соответствующих множествах, функций постоянной структуры:

– для функции нагрузки

Fн (h) = -[(arctgK(h - 0) - arctg K(h - 50)) • (0,0058h2 + 0,3591h) + n                                                                                        (4)

+ (arctg K ( h - 50) - arctg K ( h - 70)) • (0,1315 h ² - 12,37 h + 322,34)];

Расчет и конструирование

– для функции разгрузки

F р ( h ) = -[(arctg K ( h - 0) - arctg K ( h - 50)) • (0,0074 h ² + 0,2353 h ) + n

+ (arctg K ( h - 50) - arctg K ( h - 70)) • (0,1387 h ² - 13,108 h + 338,61)].

В выражениях (4) и (5) K – коэффициент сглаживания функции. Для вычислений принимаем K = 200.

Выбор точки пересечения двух непрерывных функций, описывающих ветвь нагрузки или разгрузки, обусловлен минимальным значением погрешности отклонения от экспериментальных данных. Кроме того, непрерывность аппроксимирующей функции в точках пересечения обеспечивается выполнением условия равенства первой производной по аргументу (равенство скорости) справа и слева от точки пересечения, что исключает разрыв функции.

Аналогичным образом аппроксимируются все нелинейные характеристики элементов системы подрессоривания автомобиля.

В трансмиссии автомобиля «Урал» наиболее податливыми элементами на кручение являются коробка передач и карданные валы, идущие от раздаточной коробки к главным передачам переднего и заднего мостов. Угловая жесткость данных элементов на порядок ниже всех остальных элементов трансмиссии, находящихся в постоянном зацеплении. В связи с этим вся модель трансмиссии разделена на четыре части, моменты инерции которых приведены к соответствующим упруго-диссипативным участкам.

Математическая модель движения автомобиля – многоструктурная, то есть каждый режим движения описывается своей системой дифференциальных уравнений [3]. Вывод систем уравнений целесообразно проводить на основе использования уравнений Лагранжа второго рода:

d dt

d T

•

I⁵ q k J

d T д П д Ф

- — + — + — = Q k , ^{д q}k ^ q k д q _k

где Т – кинетическая энергия автомобиля; П – потенциальная энергия автомобиля; Ф – диссипативная функция, характеризующая уменьшение энергии с течением времени; Qk – обобщенная сила, соответствующая k-й обобщенной координате qk ; qk – скорость обобщенной координаты.

Полученная таким образом математическая модель разработана для исследований взаимосвязанных вертикальных и продольно-угловых колебаний автомобиля «Урал» с колесной формулой 4 × 4 и позволяет учесть влияние на эксплуатационные свойства автомобиля различных конструктивных параметров и характеристик.