О постулатах специальной теории относительности

Как-то на лекции прекрасного физика и замечательного педагога Анатолия Ивановича Наумова, преждевременно ушедшего от нас, я задал вопрос о постулатах Эйнштейна: «Первый постулат, релятивистский принцип относительности, легко воспринимается, очень логично и никакого внутреннего неприятия не вызывает, чего нельзя сказать о втором постулате, постулате постоянства скорости света. Нет ли какого рассуждения, делающего второй постулат более понятным, кроме как ссылаться на эксперимент?» Анатолий Иванович подумал и ответил: «Нет, не знаю». Теперь, через 30 лет, предлагаю возможный вариант ответа на этот вопрос. Все более широкое применение специальной теории относительности (СТО) не только в научном обиходе, но и в инженерной практике, обуславливает насущную потребность в рассуждениях такого рода.

1.    Постулаты

Обратимся к истории. Не касаясь вопроса о приоритетах, поскольку это не отвечает целям данной работы, заметим, что А. Пуанкаре [1] называл основные положения новой теории постулатами, а А. Эйнштейн [2] - принципами. Теперь «в ходу» и то, и другое. А. Эйнштейн в своей основополагающей работе 1905 года «К электродинамике движущихся тел» [2] сформулировал два принципа, на которых строится все изложение. Первый принцип - принцип относительности: «Законы, по которым изменяются состояния физических систем, не зависят от того, к которой из двух координатных систем, движущихся относительно друг друга равномерно и прямолинейно, эти изменения состояния относятся^.

Второй принцип - принцип постоянства скорости света: «Каждый луч света движется в ^покоящейся» системе координат² с определенной скоростью V, независимо от того, испускается этот луч света покоящимся или движущимся телом 》 .

Оба принципа, или постулата Эйнштейна, выдвигаются на основе экспериментов, чтобы построить «свободную от противоречий электродинамику движущихся тел». Но если первый принцип является логическим продолжением классического принципа относительности, принципа относительности Галилея, то второй, наоборот, противоречит классической физике, классическому закону сложения скоростей, нашему опыту и интуиции. Но это противоречие, как пишет А. Эйнштейн, лишь кажущееся.

Логика дальнейшего изложения следующая. Принцип постоянства скорости света позволяет использовать световые сигналы для синхронизации часов. Отказавшись от дальнодействия, мгновенной передачи действия на любые расстояния, приходим к относительности одновременности и относительности времени в разных системах отсчета. Доказательством того, что выдвинутые два принципа совместимы, является вывод преобразований, связывающих координаты и времена разных инерциальных систем отсчета, удовлетворяющих требованиям обоих постулатов. Эти преобразования (получившие в дальнейшем название преобразований Лоренца) при скоростях, малых по сравнению со скоростью света, переходят в классические преобразования Галилея.

Некоторая непоследовательность изложения в этой работе А. Эйнштейна проявляется в том, что при всех рассуждениях и выводах скорость света используется фактически как предельная, максимально возможная скорость передачи взаимодействия, хотя в формулировку второго принципа, постулата, это «не заложено». Уже после вывода преобразований при анализе следствий А. Эйнштейн пишет: 《 Дл 凡 скоростей, превышающих скорость света, наши рассуждения теряют смысл; впрочем, из дальнейших рассуждений будет видно, что скорость света в нашей теории физически играет роль бесконечно большой скорости 》 .

Логически завершается это установлением теоремы сложения скоростей, выводом, «что скорость света от сложения со скоростью, которая меньше скорости света, не может быть изменена 》) и групповыми свойствами закона сложения параллельных скоростей.

Такой порядок изложения А. Эйнштейн сохранил и в дальнейшем. Так в книге «О специальной и общей теории относительности (общедоступное изложение)» [3], 1917 г., в начале первой части после «теоремы сложения скоростей в классической механике» (§6) следует: §7. Кажущаяся несовместимость закона распространения света с принципом относительности. Заканчивается этот параграф словами: «Здесь и выступила на сцену теория относительности. В результате анализа физических понятий времени и пространства было показано, что в действительности принцип относительности u закон распространения света совместимы и что, систематически придерживаясь обоих этих законов, можно построить логически безупречную теорию. Основные положения этой теории, которую, в отличие от ее обобщения, мы называем «специальной теорией относительности», будут изложены ниже^.

2.    Современное изложение постулатов

Историческую обстановку возникновения СТО, накал страстей интеллектуального поиска того периода кратко и выпукло обрисовал В. Паули [4]. По мере удаления от исторического «контекста» при последующих изложениях основ специальной теории относительности разными авторами принцип постоянства скорости света стал терять «независимость».

Рассмотрим, например, как постулаты Эйнштейна излагаются в «Теории поля» [5]. Вначале вводится понятие системы отсчета и дается определение инерциальных систем отсчета (ИСО). Затем формулируется принцип относительности. Далее отмечается, что описание взаимодействия материальных частиц в обычной механике посредством потенциальной энергии, зависящей от координат частиц, предполагает мгновенность распространения взаимодействий. Однако опыт показывает, что мгновенных взаимодействий в природе не существует, то есть скорость распространения взаимодействий должна быть конечной. Эту скорость можно было бы называть максимальной скоростью распространения взаимодействий. Наличие максимальной скорости распространения взаимодействий означает невозможность движения тел со скоростью, большей этой. И далее: «Из принципа относительности вытекает, в частности, что скорость распространения взаимодействий одинакова во всех инерциальных системах отсчета. Таким образом, скорость распространения взаимодействий является универсальной постоянной. Эта постоянная скорость одновременно является, как будет показано в дальнейшем, скоростью распространения света в пустоте; поэтому ее называют скоростью света». И далее: «Объединение принципа относительности с конечностью скорости распространения взаимодействий называется принципом относительности Эйнштейна (он был сформулирован А. Эйнштейном в 1905 году) в отличие от принципа относительности Галилея, исходящего из бесконечной скорости распространения взаимодействий».

Интересно отметить, что обсуждаемый фрагмент книги [5] именно в таком виде был уже в первом издании 1941 года и практически без изменений повторялся во всех последующих изданиях. Согласно такому подходу второй постулат Эйнштейна становится как бы следствием первого.

Приведем еще один пример. Процитируем соответствующий отрывок из §4. Постулаты теории относительности Эйнштейна ( [6], с.210):

«В основу теории относительности положены два принципа или постулата:

• 1)    Принцип относительности Эйнштейна;

• 2)    Принцип существования предельной скорости распространения взаимодействий.

3.    Принцип относительности и Теория близкодействия 4.    Преобразования Лоренца и постулаты

…Второй постулат теории относительности был тесно связан с развитием электродинамики...

Принцип существования предельной скорости распространения взаимодействий тесно связан с принципом относительности Эйнштейна. Действительно, нетрудно видеть, что если бы скорость распространения взаимодействий зависела от скорости частиц ... принцип относительности был бы нарушен» ( [6], с. 210-212).

Как видно, удаление от оригинала все возрастает. С одной стороны, стремление сохранить два постулата, с другой - изменение логики (последовательности) рассуждений вызывает сомнения в независимости (необходимости) второго постулата. В этом плане все четко объяснил В. А. Угаров (И ， с.35):

«Мы сформулировали постулат II , по существу, так, как это было сделано в работе Эйнштейна 1905 г. Однако в наше время, вероятно, целесообразнее формулировать его иначе. А именно исходить из того, что в природе существует предельная скорость передачи сигнала (взаимодействия). Это - главное утверждение. Далее полагают, что этой предельной скоростью является скорость электромагнитных волн (света) в вакууме. Последнее утверждение не является обязательным - в принципе СТО не утратила бы смысла, если бы предельная скорость оказалась иной, но в СТО используется именно это предположение. Из того, что скорость света в вакууме является предельной скоростью передачи взаимодействий, непосредственно вытекает, что она должна иметь одно и то же значение во всех ИСО».

Теперь можно вернуться к вопросу, поставленному в начале статьи.

Принцип относительности и Теория близкодействия - две равноправные независимые великие идеи. Рассуждение о том, что зависимость скорости распространения взаимодействий от выбора системы отсчета ведет к нарушению принципа относительности, конечно, важно, но это соответствует подчинению теории близкодействия принципу относительности. Не менее важно согласование принципа относительности с теорией близкодействия. Если бы скорость распространения взаимодействий (скорость света) была бы разной в разных системах отсчета, то, переходя от одной системы к другой, ее можно было сделать как угодно большой, и близкодействие выродилось бы в дальнодействие. Таким образом, Принцип относительности и Теория близкодействия (полевой подход с конечной скоростью передачи взаимодействия) совместимы только тогда, когда максимальная скорость распространения взаимодействий будет постоянной, одинаковой во всех системах отсчета. Именно совместимы, поскольку этот вывод следует как с точки зрения Принципа относительности, так и с точки зрения Теории близкодействия.

Интересно проследить это на языке преобразований, поскольку именно ковариантность (инвариантность) физических законов относительно преобразований перехода от одной ИСО к другой обеспечивает выполнение принципа относительности. Обратимся к распространенному, можно сказать, стандартному выводу преобразований Лоренца [8] и выясним, как далеко можно продвинуться, не прибегая ко второму постулату, постулату постоянства скорости света.

Пусть (x,y,z,t) — пространствешю-временнне координаты I IC О S.;工(x‘, y‘, z‘, t‘) — соответственно IICO S’. Штрихованная система движется в положительном направлении оси x ііештрііховаішоп сііст(?мы. оси x ii x‘ обеих систем совпадатот. а，осп y* y‘ ii z. z‘ — попарно параллельны. В момент t = t‘ = 0 начала обеих систем отсчета совnana/ni. Из одпородиости пространства ii времени следует линейность преобразований. Равноправие обеих систем отсчета и осей у и z относительно движения означает, что у = у', z = z ‘.

Начало IICO S', точка x' = 0. относите,тыю IICO S имеет координаты x = vt. Следовательно, закон преобразования координаты x' должен иметь вид

X’ = а(х - vt),(4.1)

где1 а — некоторый параметр, который может ^зависеть от скорости.

а = a(v).(4.2)

Обратное преобразование в соответствии с принципом относительности -

X = a(x‘ + vt‘).

Подставим (4.1) в (4.3) и выразим t‘:

t‘ = а [t - v(1 - 02)].

На этом возможности принципа относительности по выводу преобразований исчерпаны. Чтобы найти явный вид параметра а, требуется применить второй постулат. Но есть еще одно обстоятельство, на которое первым обратил внимание Пуанкаре [1]: если справедлив принцип относительности, искомые преобразования должны образовывать группу. Рассмотрим преобразования (4.1) и (4.4) с этой точки зрения.

Пусть имеются ИСО S, S’ и S“ ， связанные преобразованиями вида (4.1) и (4.4),

и

X ’ = ai(x — vit),

t ‘ = a 』 t — - (1 — 3)

v1        α21

(4.5)

X ’’ = 02 (x ‘ — V2t ‘ ),

t ‘‘ = ⁰² 卜^- v2 (^{1 —}      ,

(4-6)

rje vi — окоросіь S‘ отиосителыю S ii V2 — S’’ отііосптелыю S^f. соответственно. Коэ ( 1 )( 1 ) ішпепты ai = ai(vi) ii 02 = 02(v2 )( 1 ) уіікттііоііалыіо совпадатот c коэ ( 1 )( 1 ) ішііептом а = a(v), (4.2). Подставляя (4.5) в (4.6), получим преобразования непосредственно от ИСО S к ИСО S“

X ’’ = A(x — Bt);  t ’’ = AK (t — Dx),

(4.7)

где обозначено

A = 0102 (1 + Y1V1V2) ；   B = (vi + V2 ) (1 + Y1V1V2)^-1 ；

K =(1+ )2V1V2 ) (1 + Yiviv2 ) ^-i ； D = (Yivi + Y2V2 ) (1 + )2V1V2 ) - 1 ；             (丄 8)

^Yi=v2 (^1—— i=^{1 ； 2.}

Преобразования (4.5) и (4.6) образуют группу, если K = 1, а величины A, B, D принимают вид:

B = v3 ；

A = аз = азЗ);

(4-9)

D=((1 - О где? тз имеет смысл скорости IICO S’’ относитсяыю IICO S, а аз = аз (оз) должно (функционально совпадать с а = а (v). (4.2). Условия (丄9) будут иметь место, если

Yi = 3(1-9=3, vi2        αi2      τ 2

i = 1, 2,

(4.10)

где1 т — постоянный параметр, иметоший размерность скорости. Тогда при всех ^значениях i = 1, 2, 3

^a2 = ( ¹ - 号)

ii скорость v3 будет равна

V3 = (vi + V2 ) ( 1 + vTv² )

.

Таким образом, как будто получили преобразования Лоренца и релятивистский закон сложения скоростей, но принцип относительности не может сказать существует ли такая скорость т (4.10), одинаковая для всех систем отсчета. Принцип относительности только предсказывает, что такая скорость должна существовать. Если она существует, то принцип относительности имеет место, если не существует, то принцип относительности не выполняется. Решающее слово остается за экспериментом. И значение постулата постоянства скорости света в том, что он на основе обобщения экспериментальных данных утверждает существование такой скорости.

5.    Преобразования Галилея

Условия (4.9) также будут иметь место, если т = х. Тогда a(v) = 1, A = 1, D = 0, V3 = vi + V2 и формулы преобразований (4.1) и (4.4) принимают вид преобразований Галилея:

X’ = x — vt, t‘ = t.

Следовательно, принцип относительности сам по себе не запрещает бесконечно большой скорости, мгновенной передачи взаимодействия.

Рассмотрим преобразования Галилея с точки зрения релятивистской кинематики в пространстве Минковского. В работе [9] показано, что матрицу преобразований Галилея в пространстве Минковского можно привести к виду матрицы преобразований Лоренца путем ортогонализации и нормирования. Следуя ( [9], с. 24, 76), проследим по шагам последовательность этих действий.

Запишем преобразования Лоренца для одномерного движения, ограничившись плоскостью Минковского,

X = a(x‘ + vt‘),

t = a (t‘ +—2x‘),

α-1

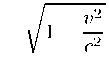
в матричном виде:

◎ = l(X) L = a(v/_c v/c)

(5.1)

g,e матритіа L является ортогонально ； 上 工 о есть обратная матритіа L^-1 равна траііспоііііроваішоп L (символ TiL 「 b,ra ， обоз на ( ает опер ап,шо транс потшроватшя] при в том detL = +1. Столбтіы втоіі матрицы

了 i = a О 7 二 a(v/)               g)

представляют собой ортогональные и нормированные векторы на плоскости Минковского (сигнатура метрики на плоскости есть (+ -)):

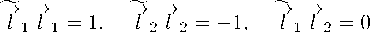
(5.3)

Аналогично, преобразования Галилея

X = X’ + vt‘, t = t‘ представим в матричном виде:

(at)=G(at) G=Q/a0)， где1 a — масштабный множитсяь размерности скорости. det(G) = +1, но матритіа не является ортогональной. Обозначим вектор-столбцы матрицы

/ 1=(v/a), /2 О

Видно, что N i отличается от l 1 ( 1 ) актичсч?кп только нормировкой ii масштабным множителем.

Нормируем его:

] iN i = 1 - 02 ； 了 i(a) 三 N i (方 iN 1 ) ^-1/2 = (1 - 02)

(ja) ; 了 i(a) ■了 i(^a) = L (5.4)

При a = c ' ；) ти векторы полиостьто совпадатот. l i (a = c) = l >  Otm ( ?tiim. что при ііормііроваіііш масштабный множитель a за счет сигнатуры (— -) начинает играть роль предельной скорости.

Для ортогонализации матрицы G заменим стандартным образом вектор-столбец 力 2 комбинацией

力 2 - ( 方 2 ・ ^Ni(a))^Ni(a)=(1 - ^)   (v^/a).                    (5.5)

В

результате получаем нормированный

вектор-столбец l 2(a)

на плоскости Минковского

^N2(a) = (1 - О2) Т2 (Za) ， 2(a) ・ ^N2(a) = - 1-                  (5.6)

Векторы l i (a) (5.4) ii l 2(a) (5.6) удовлетворятот таким 本 e условиям (5.3). что ii векторы l i, l 2 (5.2). ii обра ： зутот ортогоналыіуто матритіу

Lg = (^N i(a), ^N 2(a)) = ( 1 -頁) "(/a v/a ) -                  ( 5 ・ 7)

При выборе масштабного множителя a = c матрица Lg (5.7) совпадавт с матрицей L (5.1) преобразований Лоренца [9].

Выделим основные моменты, за счет которых преобразования Галилея трансформируются в преобразования Лоренца.

Как было отмечено выше, при нормировании (5.4) за счет сигнатуры (+ -) масштабный множитель начинает играть роль предельной скорости. Кроме того, процедура ортогонализации (5.5) соответствует такой синхронизации пространственно разнесенных часов, при которой ось времени остается ортогональной пространственным осям в любой ИСО.

Все это еще раз показывает, что математический аппарат СТО, основанный на геометрической интерпретации преобразований Лоренца, предложенной Минковским, непосредственно опирается на постулаты, лежащие в основе СТО.

Заключение

Насущную потребность в рассуждениях, раскрывающих необходимость и логическую взаимосвязь постулатов СТО, подтверждает пример работы [10]. Автор отмечает: «Трудности восприятия основных представлений о пространстве-времени, кинематики и динамики движений с околосве-товыми скоростями, как представляется, связаны с отсутствием учебной экспериментальной базы и возможностей наблюдения за движениями с такими скоростями. Обычный повседневный опыт заставляет усомниться в достоверности релятивистских эффектов и даже вызывает их неприятие.

Традиционная методика изложения СТО основывается на постулате о постоянстве скорости света и принципе относительности. Такой подход был единственным аргументом в пользу СТО у ее создателей в начале XX в. Поэтому при первом знакомстве с теорией относительности нередко складывается ложное представление, что релятивистские эффекты связаны исключительно со световыми сигналами, поскольку в формулах Лоренца скорость света является фундаментальной величиной» [10].

Автор делает вывод, что «изложение основ СТО требует привлечения новой методики, основанной на большом количестве накопившихся в XX в. экспериментальных результатов, никак не связанных с измерением скорости света» [10]. Конечно, использование экспериментальных результатов необходимо и в работе представлен большой обзор соответствующих экспериментов. Но строить изложение основ СТО, опираясь только на эксперимент, без анализа взаимосвязи и логической необходимости постулатов невозможно, слишком формально. Чего стоит, например, такой комментарий к преобразованиям Лоренца: «Ясно, также, что скорость V не может быть равной скорости света с или превышать ее, поскольку тогда либо знаменатель обращается в нуль, либо под корнем получается отрицательное число». И далее: <С физической точки зрения условие V < c означает, что не обнаружены объекты ..., скорость которых достигала бы величины скорости света...» ( [10], с. 1303). «Не обнаружены» не означает «не существуют». А может быть обнаружатся? Такой комментарий только укрепляет интуитивное неприятие и стимулирует попытки опровергнуть теорию относительности. Точно так же аргументацию раздела 3 «Предельная скорость распространения взаимодействий» нельзя признать удовлетворительной.

Вся новизна методики [10] сводится к тому, чтобы «задавить» слушателя (читателя) обилием появившегося экспериментального материала, вместо того, чтобы раскрыть внутреннюю логику СТО.

Как сказано в аннотации [10]: «Такой подход ... позволяет избежать ложного представления, что релятивизм связан исключительно со световыми явлениями». Может быть, в этом плане более продуктивно вспомнить, что постоянная с, скорость света, изначально в уравнениях Максвелла называлась электродинамической постоянной?

Автор благодарит А. М. Баранова за внимание к работе и плодотворное обсуждение.