О предельной концентрации значений хроматических чисел случайных гиперграфов

1.    Введение и история задачи

В работе исследуется известная задача, теории случайных гиперграфов, связанная с j-хроматическими числами. Напомним основные определения.

1.1.    Основные определения и изучаемая модель

Хорошо известно, что понятие правильной раскраски графа, неоднозначно переносится на гиперграфы, здесь можно ввести целую серию так называемых j-правильных раскрасок, параметризуемую натуральным параметром j. А именно, пусть Н = (V, Е) — это /-однородный гиперграф. т.е. гиперграф. вое ребра которого имеют мощность / как подмножества V. Раскраска множества вершин f : V ^ {1,...,т} в г цветов называется j-npaeuAUHOti,, если в ней любое ребро гиперграфа содержит не более j вершин каждого из г цветов. В частности, при j = 1 это означает, что вершины каждого ребра должны быть покрашены в разные цвета, а при j = / — 1 ребра просто не должны быть одноцветными. Заметим, что ситуация j > / — 1 тривиальна, ведь тогда любая раскраска будет j-правильной. В случае графов, при / = 2, у нас нет вьібора, кроме j = 1, когда правильная раскраска, означает, что нет двух вершин одного цвета, соединенных ребром.

Минимальное число цветов г, для которого существует j-правильная раскраска множества вершин гиперграфа Н в г цветов, называется j-хроматическим числом Н , его принято обозначать через Xj(Н ). Классическому понятию хроматического числа гиперграфа, х(Н ), введенному Эрдешем и Хайналом, соответствует вариант j = к — 1.

В работе изучаются предельные распределения j-хроматических чисел случайного к-одпородиого гиперграфа в равномерной модели Н(п,к,т). п > к > 2. т Е N. В этой модели у нас есть множество из п вершин, и мы независимо и каждый раз равновероятно выбираем т ребер из множества всех возможных к-подмножеств множества вершин. В рамках статьи мы предполагаем, что к > 2 и 1 ^ j ^ к — 1 фиксированы, п стремится к бесконечности. а т = т(п) некоторым обр;сюм зависит от п.

1.2.    История результатов

Хроматические числа случайных гиперграфов наиболее активно изучались в классической биномиальной модели Н(п,к,р) Напомним, что в данной модели проводится схема Бернулли на к-подмножествах п-элементного множества. Между биномиальной и равномерной моделями существует асимптотическая эквивалентность (см., например, [1]), поэтому многие асимптотические свойства будут одинаковы для обеих моделей. В случае графов при к = 2 модель Н(п, 2,р) известна также как модель Эрдеша - Реньи случайного графа С^(п,рҮ

Вопрос о концентрации значений хроматического числа случайного графа С(п,р) изучается с 80-х годов прошлого века, начиная с работы Боллобаша [2], где была найдена асимптотика х(С(п,р)) при постоянном р Е (0,1). Используя идеи Боллобаша, основанные на применении неравенств больших уклонений для мартингалов, последующие исследователи установили, что при достаточно быстро убывающей к нулю функции р = р(п) значения х(С(п,р)) с вероятностью, стремящейся к 1, принадлежат некоторому ограниченному множеству. Первый подобный результат был получен Шамиром и Спенсером [3], которые показали, что в некоторых условиях х(С(п,р)) сконцентрировано в четырех последовательных значениях. В дальнейшем Лучак [4] и Алон, Кривелевич [5] доказали, что имеет место и более сильный результат о концентрации в двух соседних значениях. Сформулируем данный результат более точно.

Теорема 1. (Т. Лучак [4], Н. Алон, М. Кривелевич [5]) Пусти е >  0 фиксировано, а р = р(п) ^ п^-1/2-е. Тогда сугцествует такая функция һ = һ(п,р), что

P (х(^(п,р)) Е {һ, һ + 1}) —> 1 при п ^ то.

Однако теорема 1 носит лишь характер существования, из ее доказательства невозможно явно указать, как һ(п,р) зависит от п и р. В ряде последующих работ исследователи смогли отыскать явный вид функции һ при достаточно быстро убывающей функции р = р(п). Так, в работе Аклиоптаса и Наора [6] ответ был найден в так называемом разреженном случае, когда среднее число ребер линейно по числу вершин, т.е. когда р(п) = сп/ я ля с > 0. не зависящего от п.

Теорема 2. (Д. Аклиоптас, А. Наор [6]) Пусти С >  0 фиксировано, тогда ноломсим г_с = тіп{г Е N : с < г ln г}. Ес ми р = сп/ Q). то

P (х(^(п,р)) Е {г_с,г_с + 1}) —> 1 при п ^ то.

Ситуация пр ^ то оказалась более трудной. Здесь при р ^ п^-3/4-е улеглось доказать (см. [7,8]), что хроматическое число случайного графа С(п,р) сконцентрировано в трех соседних значениях, которые можно указать явно.

Активное изучение j-хроматических чисел случайных гиперграфов также началось в 80-х годах прошлого века. В первых работах Шмидта, Шамира и Упфола [9-11] было найдено асимптотическое поведение Xj(Н(n, k,p)) при определенных условиях на величину Р = p(n). Наиболее общий результат был позднее получен в работе Кривелевича и Судакова [12]. Для его формулировки введем величину d = р(^-1), равную математическому ожиданию степени вершины в Н(п, к,р) и положим d, = j^- ^d.

Теорема 3. (М. Кривелевич, Б. Судаков, [12]) Существует такое do = do(k,j) > 0, что если р = p(n) удовлетворяст условиям pnk-1 ^ do it pnk-1-j т 0. mo dj      \1/j                                   dj                   1 \ \1/j

+ 1)ln d j )   <  ^X>^(H{n’^k-^p)) < ( (j + 1)ln d, Р + һОЩ ))        1»!”" ^тто

Теорема 3 дает концентрацию j-хроматического числа в ограниченном множестве значений, только если величина d фиксирована, что эквивалентно тому, что мы находимся в разреженном случае, когда среднее число ребер p ведет себя линейно по числу вершин п. Исследование концентрации хроматических чисел Н(n,k,p') в разреженном случае оказалось тесно связано с поиском точных пороговых вероятностей для свойства правильной j-раскрашиваемости в заданное фиксированное число цветов. Наиболее активно изучалась ситуация j = к — 1. 'здесь Дайер. Фриз и Гринхилл [13] доказали, что Хк_-1(Н(п, k,p)) сконцентрировано в двух соседних значениях, которые можно явно указать, если p = сп/ и с >  0 не зависит от п. В дальнейшем полученные в [13] оценки точных пороговых вероятностей были усилены в серии работ [14, 15]. Из этих работ следует, что для почти всех значений параметра с хроматическое число случайного гиперграфа сконцентрировано всего лишь в одном значении, т.е. было найдено предельное распределение.

Другие j-хроматические числа при 1 5 j < к — 1 также активно изучались для разреженного случая. Семенов и Шабанов [16] при p = сп/ (^) и к ^ 7 установили предельную концентрацию Хк-2(Н(n,k,p')') в двух соседних значениях, которые можно явно указать. Данный результат был обобщен в недавней работе Денисова и Шабанова [17] для к/2 5 j < к — 2 и к >  9. Аналогичные результаты о концентрации 1-хроматического числа случайного гиперграфа были получены в работах [18,19].

В неразреженном случае, когда pn^k-1 т то, изучалась только концентрация Хк_—1(Н(n,k,p')Y В работе [20] было доказано, что при не слишком медленно убывающей функции p(n) хроматическое число случайного гиперграфа сконцентрировано в некоторых двух соседних значениях, а также были найдены эти два значения в определенных случаях. Сформулируем первый результат [20] в виде отдельной теоремы.

Теорема 4. (Ю. Демидович, Д. Шабанов, [20]) Пустъ натуральное число к ^ 3 фиксировано. Обозначим с = с(п) = p^y . Если с т +то. iю с 5 п ²-^+1^-£ для некоторого фиксированного е > 0, то существует такая функция h = h(n,p) с натуральными значениями, что

P (xk_-1 (Н(п, k,p)) Е {h, h + 1}) —> 1 нуни n т то.

Целью нашей работы является изучение концентрации значений j-хроматических чисел случайного гиперграфа в неразреженном случае для произвольного j.

1.3.    Новый результат

Основной результат данной работы сформулирован в теореме ниже и дает границы, в которых находится j-хроматическое число случайного гиперграфа Н(п, к,т) при не слишком быстро растущем числе ребер т = т(п).

Теорема 5. Пустъ Н(п,к,т) — случайный к-однородный гиперграф на п вершинах в рав-иомсриой модели, а 0 < е <  дД фиксировано. Если т 5 п^1+е. но п = о(т) то существует такая функция h = һ(п,т) что

^P (^h 5 X, (^Н(n, к т)) 5 k + . _— » _{2) е} • [^к-^—2р і)

—> 1 пу си п т то.

Отметим, что теорема 5 дает концентрацию значений j-хроматического числа в некотором ограниченном множестве значений, хотя и не в двух значениях, как в теореме 4. Но по сравнению с теоремой 4 мы получаем концентрацию при несколвко болвшем числе ребер при j = к — 1, а именно вплоть до п^2-1/^¹') вместо п^3/2-1/(к+1\ Впрочем, точное сравнение результатов затруднено тем, что мы формально работаем в другой модели, а результат слишком тонкий, чтобы простые факты об асимптотической эквивалентности моделей автоматически переносили результаты из одной модели в другую.

В следующем разделе мы докажем теорему 5.

2.    Доказательство теоремы 5

В доказательстве мы следуем идеям из [3]. Пусть Н (п, к,т) — случайный гиперграф в равномерной модели с независимыми ребрами. Пусть V(Н(п,к,тУ) — это множество его вершин, а Е(Н(п,к,т)') — множество его ребер.

Введем функцию Һ как минимальное натуральное число, удовлетворяющее соотноше-

P(Xj(Н(п,к,т)) ^ Һ) >  ¹ .                             (1)

ln п

Заметим, что тогда P(xj(Н(п,к,т)) <  Һ) <  Е; ^ 0, т.е. с вероятностью, стремящейся к 1, будет выполнено Xj(Н(п,к,т)~) ^ Һ.

Далее, нам понадобится следующее обозначение. Для подмножества вершин U С V(Н(п,к,т)) введем

Ej(U ) = {A nU : | A nU| >  j + 1, А Е Е(Н(п, к, т))} ,

• т.    е. это множество всех ребер, которые проходят только через вершины множества U, а также «обрезки» ребер, которые проходят и через вершины, не лежащие в этом множестве, но имеют хотя бы (j + 1) вершину в U. Введем обозначение Нj(U ) для гиперграфа Нj(U ) = (U,Ej(U )). Он, вообще говоря, не является однородным, но все равно можно говорить о его правильной j-раскрашиваемости в Һ цветов. Обозначим

^Yn = max^{{|U 1} : Xj^(Нj^(U )) <  ^Һ}

И положим

Үп =п — ү;.

Далее, мы хотим оценить величину Ү_п. Для этого применим следующее неравенство больших уклонений для функций от независимых случайных величин, доказательство которого можно найти в [1].

Теорема 6. Пусть Z1,...,Z_S — независимые случайные величины. Пусть f(х₁,...,х₅) — такая функция многих переменных, что для любого г = 1,...,s найдется С і >  0 с условием, что для любых х_г,у_г Е R выполнено

|f (Х1, . . . ,Хг-1,Хг,Хг₊1, ...,X_S) — f (Х1, . . . ,Хг—1,Щ ,Х_І+1, . . . , X_s) | <  С і .

Тогда случайная величина X = f (Z1,..., Z_n ) удовлетворяет следующим неравенствам:

для любого t >  0

P(X > EX + t) ^ exp

-

t2

2 EU c2

,

P(X ^ EX — t) ^ exp

-

t2

2 E-=1 c²

.

Заметим, что величину УП можно представить как функцию от случайных ребер случайного гиперграфа Н(п,к,т):

Yn = f №,..., X_m).

Отметим, что функция f (жі,...,ж_т) удовлетворяет условию теоремы 6 с параметрами a = к — j, ведь при добавлении одного ребра к гиперграфу величина, выражаемая функцией f, не может увеличиться более чем на к — j. Если было какое-то множество U_n с условием, что Xj(Н(Un)) ^ к, то мы всегда можем оставить от ребра не менее j вершин внутри U_n, чтобы к-раскрашиваемость сохранилась.

Лемма 1. В условиях теоремы 5 выполнено

P ^Y_n< 2(к — j)Vm ln п)

--> 1 при п ^ то.

Доказательство. Докажем сначала, что EY„ <  (к — j ) Vт Inn. Предположим противное, что EY„ ^ (к — j )V т lnn. Тогда в силу второго неравенства теоремы 6 имеем

P (Xj(Н(п, к, т)) ^ к) = P(Yn = 0) ^ P ^Yn ^ EYn — (к — j) Vmlnn} ^

( к— j )² т ln n ^ e^-^т<к—j)^

_ ln n

= e 2

< A, lnn

что противоречит выбору функции к. Таким образом, выполнено ЕУ„ <  (к — j )V т lnn. Остается лишь применить первое неравенство теоремы 6:

P ^Y_n ^ 2(к — j)Vm lnn) < P ^Yn >  EY_n + (к — j)Vm ln п ) < e 2 —> 0.

Значит, с большой вероятностью Y_n< 2(к — j ) V т ln п.                                □

Из леммы 1 следует, что с вероятностью, стремящейся к 1, в случайном гиперграфе найдется такое подмножество вершин Un, что

• •    Xj^(Hi^{(У(Н(п,к,т}) \^Un⁾⁾⁾ ^ ^к

• •    |U_n| <  2(к — j)Vт 1пп.

Теперь мы хотели бы оценить Xj(Hj(U_n)). Для этого покажем, что с вероятностью, стремящейся к 1, каждое подмножество S вершин Н(п, к,т) мощности не более 2(к — j ) V т 1пп содержит не очень много ребер в Ej (S ).

Лемма 2. В условиях теоремы 5 с вероятностью, стремящейся к 1, каждое подмножество вершин S С У(Н(п,к,т)) мотщостіі нс. более [2(к — j)Vт 1пп ] удовлетворяет неравенству

I ^Ej ^(S >к J—(JW^№

Доказательство. Обозначим для краткости а = j _- ( _i ³ ₊ 2) _e , ⁸ = \2(к — j ) V т 1пп ф В силу построения модели Н(п,к,т) вероятность того, что фиксированное множество S удовлетворяет неравенству | Ej (S)| >  a|S|, не превосходит

(р^^))^::! оы ’ где n = |S|, а 3(n) = Et=.,'+1 (")(^—")• Отсюда вероятность того, что найдется подмножество вершин U мощности не более s с уеловием \Ej(S)| > j—(Д2)е • |S| не превосходит

Е u=j + 1 4 7

/ ^т )з ЩЩ

\ Гаи] / ³

((ЭД1

S

= Е f . .

"=j + 1

Оценим слагаемое F_u, где воспользуемся тем, что т Д n^1+e и 3(n) = Ө(n^:j+1n^{k j 1}):

Fu = O

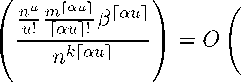
_nu+(1+e—k') Щи ] (_n j +1_n fe — j —1) Ди ] n! Pan^!

=

= O

(

_n^u—(3 ^- e ) ДСДа" (^j+1)

( u ) u ( ^Гаи] )Д и ]

)

Продолжим оценивать выражение в скобках в (3):

_nu-(j-e) Г ®" ] Д®" ] ( j +1)     _nu-(j-e)aUn(au+1)(j+1)_eDu    _nu-(j-e')^Unj+1+aju-u_e^u

( u ) u ( ^Г ® ^и] )Г “и ]                    n^u(an)^au                            a^a'"

где D — некоторая константа. Далее полученное выражение можно оценить следующим образом:

Д (.ТО)аЦ|.) ' 1'aj" Д^Я" ⩽ a^au

n1—(j—e>n ^ +aj-1 eD

I           a“

)

⩽

(т.к. n ^ j + 1)

⩽

n1-(j-e)anaj eD aa

)

Наконец, воспользуемся тем, что n Д s = O(Vn1+e In n), и тогда выражение в основании степени имеет порядок по n не более чем n1-a(j-e-j ^) lnaj/2n.

Степень при n здесь равна. 1 — a(j — е — j 1+) = 1 — a(^j—(^Т²^). что при a = j-^j+^e ^явля" ется отрицательной величиной, и, значит, выражение в (4) стремится к нулю при n ^ то. Таким образом, мы имеем, что выражение в (2) ограничивается геометрической прогрессией с убывающим знаменателем, где первый элемент прогрессии также стремится к нулю. Значит, и вся сумма (2) стремится к нулю при n ^ то. □

Последняя лемма оценивает Xj(Hj(U_n )).

Лемма 3. В условиях теоремы 5 выполнено

P(x , <^H<^U - ⁾⁾<  --іуДхе ■ [^^Н

--> 1 при n ^ то.

Доказательство. Рассмотрим произвольное S С Un. Тогда S подходит под условие леммы 2, и в гиперграфе Hj (S) можно найти верши ну степени не более j-(З+Д-Действительно, согласно лемме 2 получаем, что j — (j + 2)е

|S |,

откуда и вытекает наличие требуемой вершины. Данное наблюдение означает, что гиперграф Ну(U_n) с вероятностью, стремящейся к 1, является (у—З+у^-вырожденным, в каждом его подгиперграфе найдется вершина степени не более у-уу+Д' Покажем, что этого условия уже достаточно для построения искомой раскраски.

Далее, рассмотрим следующий процесс набора вершин: найдем в гиперграфе Hj(Un) вершину - степени не более у^^ 2) _£ , удалим ее из U_n и повторим процедуру во множестве

U_n \ {-}• Получится некоторая последовательность вершин - q = -,.

.

./Dt! которую мы

будем раскрашивать в обратном порядке. Вершину -t мы раскрасим в цвет 1, а далее, если вершины -і+1, ..., -t уже раскрашены, то берем вершину -г и рассматриваем гиперграф Ну ({-г,..., —t}). В нем вершина -г имеет степень не более у-(yp^y ’ а кажДое ребро запрещает для нее не более чем \(к — 1)/] 1 цветов. Ст ало быть, у-(у+д " Г 1 + 1 цветов достаточно для того, чтобы для -г нашелся свободный, незапрещенный цвет, а Ну ({—г,..., —t}) стал бы ^-правильно раскрашен. После раскраски -q мы получим, что

, _тт ,_тт            3к          к — 1

X,№№» < ] — (] + 2)г • -   +1-

□

Завершим доказательство теоремы 5. Мы доказали, что с вероятностью, стремящейся к 1, найдется такое подмножество вершин Un, что одновременно будут выполнены неравенства

Х у ^(Н у ⁽V^(Н(п^,к,т) \^Un⁾⁾⁾ ^ Қ ху^(Ну№) <

3к

] — (] + 2)е

■[

+ 1.

Данные неравенства влекут искомую оценку

Х у (Н(п,к,т}) ^ Һ +

3к

] — (] + 2)е

[     1+1-

□