О представлении линейных операторов, коммутирующих с дифференцированием, в односвязной области

Введение. Рассматриваемые в статье задачи входят в направление исследований, представленное работами [1-7]. Пусть G — односвязная область в комплексной плоскости С, и последовательность ограниченных расширяющихся областей {Gn }Т G с кусочно-гладкой границей исчерпывает G . H (G) — пространство Фреше аналитических в G функций с топологией равномерной сходимости на компактах. £ (G) — пространство непрерывных в H (G) линейных операторов. Обозначим через B (Gn) банахово пространство аналитических в Gn и непрерывных на Gn функций с нормой f (z)|| := ma_x f (z)|. Тогда Vn 3N := N (n) оператор Le £ (G) расширяется n     zeGn до непрерывного оператора Ln: B (GN) ^ B (Gn).

Обозначим k n ( t , z ) : = L,

[ 1

"ⁿ 1 1 - Z

( z ) , t е G N , Z е G N , z е G n . Эта функция голоморфна

на односвязной области G'_N x G_n с С ², и связана с линейным оператором L формулой

[ Ly ] ( z ) = -1т j y ( t ) • k_n ( t , z ) dt , z e G_n [2]. Локально аналитическая на G 'x G функция ²ⁿⁱ G _{+ 1}

k ( t , z ) , совпадающая с k_n (t,z ) на соответствующей области G'_N x G_n , называется ядром оператора L .

Обозначим через £d (G) подпространство в £ (G) операторов, коммутирующих с операцией дифференцирования:   Ld = d-L.  Назовём вычетом области G множество dz dz s (G) := {z е С: z + G с G}. Для вычета справедливо тождество (G' - G)' = s (G) [6].

ТЕОРЕМА. Пусть G есть односвязная область. Функция k n ( t , z₀ ) , z₀ e G аналитически продолжается до локально аналитической функции A ( t ) на G' - G = ( s ( G ) ) ' и k ( t , z ) = A ( t - z ) . При этом в случае несвязного s ( G ) всегда найдётся оператор L e £ d ( G ) , для которого функция A ( t ) многозначная, а в случае связного s ( G ) * { 0 } функция A ( t ) всегда однозначная.

Вспомогательные утверждения. В следующей лемме доказаны необходимые свойства вычета области и получено аналитическое описание класса односвязных областей, вычет которых содержит луч.

ЛЕММА. 1) Для односвязной области G множество s ( G ) U { ” } замкнуто.

• 2)    Если нуль есть предельная точка s ( G ) , то s ( G ) содержит некоторый луч l ф₀ : = { r exP { i Ф о } : ^r >  0 } .

• 3)    Произвольная односвязная область G c l _ф с s ( G ) задаётся полунепрерывной сверху на ( / , +« ) функцией k ( x ) со связной областью определения { x : k ( x ) <х } по формуле G = { z = re^фi : k ( r sin ( ф₀ - ф ) ) <  r cos ( ф₀ - ф ) } .

Доказательство. Покажем замкнутость s (G) U {”}. Пусть z0 — предельная точка s (G): 3{zk} с S (G) lim zk = z0. Фиксируем произвольную точку z e G и покажем, что z0 + z' e G (то-k^z гда z0 + G с G, и значит z0 e s (G)). Ve > 0 D (z', e) с G ^ Vk > k (e) zk + D (z', e) с G .

Выберем k таким, что

E _( E 1           _(- E 1 _( E 1

|^z 0 ^{- z} k | <  2 ^ ^z 0 ⁺ D I ^z',2 I^{е z} k ⁺ D I ⁰, 2 1 + D I z, 2 1 = ^z k ⁺ D ( z ^,E ) c ^G , что и требовалось доказать.

Докажем утверждение 2). В силу условия существует последовательность {zk = rk exp {iфk}} ^ 0, {zk }c s (G). Считая фk e[0,2n), выберем сходящуюся подпоследовательность. Без потери общности считаем lim фk = ф0. Фиксируем на луче k ^х lфо := {r exp {iф0}: r > 0} произвольную точку r0 exp {iф0} =: z0 ^ 0 и покажем, что она будет предельной для множества точек вида {i • zk k 1 ” 1 с s (G) (а значит принадлежит s (G)). С этой целью для произвольного фиксированного e > 0 выберем такой номер k, чтобы

|ф₀ - ф_к |< arcsin | ^3 | и | z k | <^E .

I ^{2 r} 0 J

Тогда луч l_фк : = { r exp { i ф _k } : r >  0 } пересекает e -окрестность D ( z ₀,E ) по хорде длины >  e. Поэтому на этой хорде лежит хотя бы одна точка вида i • z_k , и значит i • z_k e D ( z ₀, e ) .

Утверждение 3) докажем сначала для случая l _n/2 с s ( G ) . G пересекается с вертикальной прямой либо по пустому множеству, либо по интервалу (возможно совпадающему с этой прямой). В первом случае положим k ( x ) : ■/ , а во втором k ( x ) : = inf { y : x + yi e G } . Если -х <  k ( x ) < ■/ , то точка x + k ( x ) i e Г ( G ) . По определению имеем G = { z = x + yi : k ( x ) <  y } .

Пусть -от< k ( x 0 ) < от . В силу открытости G

V e >  0 З 5 >  0, 5 <  е, D ( x ₀ + ( k ( x ₀ ) + е ) i ,5 ) с G ^

^ V x е ( x ₀ - 5, x ₀ + 5 ) 3 z = x + yi е D ( x ₀ + ( k ( x ₀ ) + e ) i , 5 ) ^ k ( x ) <  y <  k ( x ₀ ) + 2e Последнее означает полунепрерывность сверху k ( x ) в точке x ₀. По той же схеме рассматривается случай k ( x ₀ ) = -от . Связность области определения k ( x ) следует из связности области G .

Обратно, пусть дана полунепрерывная сверху и со связной областью определения функция k ( x ) . Положим G = { z = x + yi : k ( x ) <  y } . Из определения следует, что / _п/2 с s ( G ) .

Покажем, что G есть односвязная область. Фиксируем z ₀ = x ₀ + y₀i е G , откуда З е₀ >  0 y ₀ >  k ( x ₀ ) + е₀ . Покажем сначала, что З 5 >  0 D ( z ₀,5 ) с G , то есть множество открыто. Считаем для определённости k ( x ₀ ) <от . По определению полунепрерывности v e >  0 З 5 >  0 V x е ( x ₀ - 5, x ₀ + 5 ) k ( x ) <  k ( x ₀ ) + e . Полагая e + 5 <  e₀ , имеем V z = x + yi е D ( z ₀,5 ) y >  y ₀ - 5 >  k ( x ₀ ) + e₀ - 5 >  k ( x ) - e + e₀ - 5 >  k ( x ) , то есть z е G .

Покажем связность G . Для любых z 1 = x 1 + y 1 i , z ₂ = x 2 + y₂i е G , x 1 <  x ₂, k ( x ) ограничена сверху на [ x 1 , x ₂ J [8]. Поэтому в G существует ломаная, соединяющая эти точки.

Заметим, что луч /фо := {г exp {iф0}: r > 0} = [0, от ■ exp {iф0}) с s (G) тогда и только тогда, когда вертикальный луч /п/2 с G1 := G exp

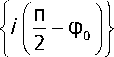
. Поэтому проведённое доказательство рас-

пространяется на случай произвольного луча / с s ( G ) . В этом случае

G exp ji ^2 - Ф0 jj = Gi ={z = x + yi: k (x)< y} о оG = jz = zexpji^Ф0 -Пjj: k(x)

Лемма доказана.

Доказательство теоремы. Выберем по точке в двух компонентах связности вычета s (G):

С1 е K1, С₂е K₂, и образуем линейный оператор [Ay](z) := z j2 y (и)dv - z +J1 y (v)dv, z₀е G , в z₀                     z₀

H (G). Он принадлежит zd (G).

По определению ядра

( 1 Al        ^z+52 1                ^z+5¹1                   (t - z - t A

^k(t,z)= LIA 1 (z)= J Ay(5)^d5- J Ay(5)^d5 ^{= ln} 1г"Г”511■

L V t^{- 5}7 J        z₀t^{- 5}             z₀t^{- 5}              I t^-z^{- 5}2 J

Отсюда Д(5) := In 11—⁵¹1. Эта функция многозначна на G'x G =(s (G))‘, так как при обходе пе-

V 5 - 52 J ременной ζ одной из компонент K1 или K2 она приобретает слагаемое 2πi .

Пусть теперь вычет s (G) связный и ^ {0}. По предыдущей лемме s (G) содержит луч. Без потери общности считаем, что /_п/2с G, то есть область G содержит вместе с каждой точкой вертикальный луч с началом в этой точке.

Определим теперь функцию   A( Z).   При достаточно малом е ряд

.     .    ” ”      (z — z )ⁱ                                                               , 1

k (t, z) = S S aj ~-----■. абсолютно сходится при z — z0 < e, t —t0 > -, и потому в нём мож-i=0j=0 (t — z0)j+                                                                   e но произвольно менять порядок суммирования.

Вычислим коэффициенты этого ряда, используя инвариантность оператора L относительно сдвига аргумента на пространстве многочленов [8]:

[Ltⁱ ](a) = [L(t + a)ⁱ ](0), a e C, n > 0,

a = — f ---¹—-——[  (t — z) jk (t, z) dtdz = —   —

'¹ 2ni Jn^ (_{z —}z)ⁱ⁺¹ 2ni Jitw^ ^{01        1} 2ni ^и^ (_z

—

1      [L(t — z0) j ](z)dz = z0) [            ]

Тогда имеем to k (t,z ) = S j=0

= T[L(t — z0)j](')(z0) = T L j! I0

^[(t—z0) j ]⁽i )]⁽z0 )=

i > j,

= i l(j — I)! l[^L(t — z0)j¹z0HLt^J—1(0), i⁵j.

(t — z 0) j+1

to

to

to                               . to

-S aj (z — z0 У = S

i=0

to

= s .

j=⁰(t^{— z} 0)

- S i=0

j=0

j!

¹j j^!   [Lt^1—i 1 (0) z — z =

(t — z₀)j^+1Si!(j — i)!^{[      ]( )(}      0)

l!(j—i)

! [Ltⁱ ](0)(z — z 0) j^—i

j—i

= 5 - [Lt 1 (0)J -j—⁽z^—z⁰).

^si!^[        -(j — i)! (t — z₀)j⁺¹

to

=SN[Lti](0) S i=0 i !                   j=0

to

(^{z — z} 0) j (t — z 0) j⁺¹

1 (I)

x-'Lt ](⁰)

^S (t — z )ⁱ⁺¹

при z — z0I <e, t — t0| >E.

Так как |[Ltⁱ ] (0)| < max |[l (t — z0)ⁱ ] (z)| < C_n max |t — z0 f< CnpN, где p_N — диаметр множе-

_                                                    to I Lt аналитическая в |Z| > pN. Поэтому

ства   GN,  то сумма ряда   A(Z) :=S"—;

i=0 ^Z'

to i Lt' 110)

^k (t, z ) = Sy ^Ti+T = A(t^{— z}) , где ^z e Gn , t e GN, t > Pn⁺Rn , Rn := sup {| z : ^z e ^Gn } . i=0 (t — z)

Докажем теперь, что функция A(Z) аналитически продолжается до локально голоморфной на G — G = (s(G)) , то есть VZ₀e G — G, Z₀ **” и любых точек t_T, t₂ e G', z_T, z₂e G со свойством Z₀= t_T — z_T= t₂ — z₂ следует k(t_T, z_T) = k(t₂, z₂). Множество (G' — z_T) A (G' — z₂) связное, так как составлено из отрезков, параллельных мнимой оси и содержащих бесконечно удалённую точку. Поэтому оно содержится в связной компоненте открытого множества (GN — z_T) A (GN, — z₂). A(Z) продолжается в области G'N — z_T, G'N — z₂ соответственно по формулам A(Z) := k(Z + z_T, z_T), A(Z) := k(Z + z₂, z₂). По теореме единственности функция A(Z) однозначна на этой компоненте:

A(Z) = k(Z + zi, z), A(Z) = k(Z + z2, z2).

В частности

A( ^Z0 ) := k (^Z0 ⁺z1, z1 ) = k (t1, z1) , ^A(^ ) := k (^Z0 ⁺z2, z3 ) = k (t2, z2 ) .

Таким образом, Зе₀ >0 A(Z) голоморфна в (G'-G)UD'^,— l ^Ео

В заключение заметим, что последовательность {N (n)} можно подобать так, чтобы

V n 3 N G‘- G с (G'-G) U Dp,— l ^Ео

Сначала выберем е е(о, Е_о) так, чтобы G'- G_n + D (0, е)g G - G . Затем N, чтобы

G; _C(G‘ + D(о, Е))UD'fо,- + R ^v                        l ^Ео

Тогда

GN- Gn ^(G' + D (о, Е)) U D'f о,-¹+ Rn I-Gn l ^Ео      J

(

= (G' + D (о, Е)-G) U Dp,- + R l l Ео

l

* n I" Gn JJ

c(G'-G)UD'l о, — |.

l ^Ео J

Теорема доказана. Из неё следует такое представление операторов из rd (G).

СЛЕДСТВИЕ. Пусть G есть односвязная область, а её вычет s(G) связный и *о. Тогда для каждого оператора Le rd (G) существует локально голоморфная на G'- G = (s (G))' функция Л(Z) со свойством:

^VzeGn [Ly]^(z) = ^7 J y(t)^A(t-z)^dt.

• ^ГGN+1

ЗАМЕЧАНИЕ. Вычет неограниченной выпуклой области G очевидно связный, и 3ф_оl с s (G). В этом случае теорема доказана в [9]. Для односвязной ограниченной области s (G) = о , то есть G'- G = С \{о}, голоморфность функции A(Z) в С \ {о} доказана независимо и разными методами в [4], [5]. Гипотеза о том, что аналогичное утверждение имеет место в случае неограниченной области G с s (G) = о , остаётся недоказанной, так как доказательство в [9] имеет пробел.

Заключение. Получено аналитическое описание класса односвязных областей, вычет которых содержит луч. Этот класс областей характеризуется тем, что ядро любого оператора из класса rd (G) порождается однозначной функцией. Результаты статьи докладывались на международной Казанской летней научной школе-конференции [10].