О представлении операторов обобщённого дифференцирования Гельфонда - Леонтьева в односвязной области
Автор: Братищев Александр Васильевич
Журнал: Advanced Engineering Research (Rostov-on-Don) @vestnik-donstu
Рубрика: Математические и естественные науки
Статья в выпуске: 2 (77) т.14, 2014 года.
Бесплатный доступ
Установлен ряд новых свойств мультипликатора. Описан класс односвязных областей, мультипликатор которых есть связное множество. Этот класс характеризуется наличием спиралей у мультипликатора. Пусть далее оператор обобщённого дифференцирования Гельфонда - Леонтьева непрерывен в пространстве функций, аналитических в односвязной области G комплексной плоскости. Известно, что он представим в виде оператора обобщённой свёртки. Её ядро порождается многозначной функцией одного переменного. Назовём мультипликатором G множество M(G) со свойством M(G)·G⊆G. Пусть мультипликатор области связный и не совпадает с единицей. В работе доказано, что при данных условиях рассматриваемые функции будут однозначными. Если мультипликатор области несвязный, то всегда найдётся оператор обобщённого дифференцирования Гельфонда - Леонтьева, порождающая функция которого будет многозначной.
Мультипликатор области, обобщённая производная гельфонда - леонтьева, ядро оператора
Короткий адрес: https://sciup.org/14250066
IDR: 14250066 | УДК: 517.982.274+517.983.22 | DOI: 10.12737/4536
Текст научной статьи О представлении операторов обобщённого дифференцирования Гельфонда - Леонтьева в односвязной области
Под оператором обобщённого дифференцирования Гельфонда — Леонтьева (ООД) понимаем линейный непрерывный в H(G) оператор, действующий на последовательности степеней по правилу Dzn := dn xzn 1, л eN, DI := 0 [6]. При этом функция d (z) := ^dnzn называется порож дающей функцией ООД. Пространство операторов Гельфонда — Леонтьева обозначим ^GL (^) 1 ^ диссертации [7] получена такая характеризация и представление ООД.
ЛЕММА 1. Определённое на последовательности степеней {z”J отображение D‘.Dzn‘.= dn_Yzn l, лей, Dl:=0, расширяется до линейного непрерывного в H(G^ тогда и только тогда, когда ряд d (z) := ^dnzn сходится в окрестности начала координат, и функциональ-
< £, аналитически продолжается в каждую односвязную об- ласть G'n х Gn, л е N. Имеет место интегральное представление
Работа выполнена в рамках инициативной НИР.
Назовём мультипликатором множества Сг с С по множеству G, сС множество MyGvGyy.= \z eC\z -G^G-^. Для мультипликатора справедливо равенство (G^ -Cf1) 1 ^М y3vG^ [9]. В частности, мультипликатором множества G назовём множество MyGy^z eC\z-G lG[. Очевидно, leM(Gy
ТЕОРЕМА. Пусть Сесть односвязная область. В случае несвязного мультипликатора M^G) всегда найдётся ООД, для которого функция d (f) многозначная, а в случае связного M(G) * {1} функция dy') локально аналитическая и однозначная на GG' V
Основная часть. В следующей лемме доказаны необходимые свойства мультипликатора области и получено аналитическое описание класса односвязных областей, мультипликатор которых содержит спираль.
ЛЕММА 2. Пусть G — односвязная область в с, тогда:
-
1) множество M(C)U{0}U{oc} замкнуто;
-
2) если единичная окружность S (0,1) с М (G ), то G = D (0, /?) либо G = С.
Обратно, если G = D (0, /?) или G = С, то соответственно М (С) = 0 (0,1) и М (G ) = С;
-
3) пусть мультипликатор M(G) является связным, тогда:
-
а) пусть 0 е М (G ). 3s >0 D(0,e)cM(G) о G ограничена. Если G не ограничена и ?ьС,то0еС и M(G) с 0(0,1);
-
б) в случае 0 г G существует спираль с началом в точке 1, наматывающаяся на точку 0 или на точку оо s :=|z = expire !₽0'[: г > 0?с М(С), ф0 ^nk + ^j и существует полунепрерывная
Фо L I J 7 z
сверху на (-so,-ко) функция к^ со связной областью определения {х : к (х)< со), которая определяет область G по формуле G = {z = exp {re”'}: к у sin (ф0 - ф)) < г cos (ф0 - ф));
-
в) в случае 0 е G существует наматывающаяся на точку 0 спираль 8 с М (G ), П/ < ф0< Зп/, и (-2псозф0) — периодическая полунепрерывная сверху на (-со,-ко) функция У(ху которая задаёт границу области G по формуле
ГС = jexpl/q (х)со5ф0 + /q(x)s^0---— / >:хе(^о,-ко) >;
-
4) дополнение G' в случае |ф0 - п| < ^ представляет собой пучок спиралей с вершиной в беско
нечности, а в случае |ф0| < % — ПУЧОК с вершиной в нуле.
Доказательство. Большая часть утверждений 1) — За) доказана в [7]. Прочие доказываются аналогичным образом.
Докажем 36). Так как континуум G содержит точки 0, оо, то на С можно выделить ветвь функции и/ = Inz, являющуюся однолистной и открытой. Область R := In С односвязная. При этом мультипликатор М(С) преобразуется в вычет s(R) этой области R: z-GcGa- In z+RcR. s (/?) = InM (G ). По условию точка 0 = Ini e R является предельной для мультипликатора s (Я).
По лемме [9] существует луч / := j гёр°': г >0 ks(R). Тогда спираль s :=
фо I L J J
Если бы (p0=n/r + >V, то s :={z = exp{+r/!: г>0! = 5(0,1)сМ(С),
и по
пункту 3)
G = D(0,R^,
что невозможно по условию. Согласно лемме [8]
R
задаётся полунепрерывной сверху КЗ ^ зс^+зс) функцией
к^
со связной областью определения [x:/r(x)
G = ^z = exp {и/} = expire”'[: к (г51п(ф0 -ф))< гсоз(ф0 -ф)}.
Зв) Продолжим lnz из какой-либо точки области G | {0}. Получим аналитическую функцию и/ = Lnz на римановой поверхности /^ с логарифмической точкой ветвления z = 0. и/ = Lnz однолистно и открыто отображает /^ на 2п/ -периодическую односвязную область R := Ln (G \ {0}), содержащую некоторую левую полуплоскость 1ти/<о. Покажем, что множество s (R) := Ln (M(G}\ {0}) совпадает с вычетом области R. Выберем и/0 := In z0 + 2пАг/, z0 е М (С) \ {0} и ^ :=lnzx +2п//, zx е(?\{0}. Так как zQ-zxeG, то по определению и/0 + wx = Inz0 • zx + 2п (к + /) i e R . To есть s (R) состоит из точек вычета области. Остаётся показать, что s(R) содержит все точки вычета.
Пусть и/0 0 и Vи/ := Inz + 2п // еR w0+w eR. Положим z0 := e"° => zoz eeR = G \{0}. Так как z0 • 0 e G, to z0 e M(G) =^ и/0 = lnz0 es(/?). Так как 1 есть предельная точка М((?), то 0 — предельная точка s(R^ => ^0e^z3r^ s^ сМ(С) => существует полунепрерывная сверху на (-зо,-н») функция к^ со связной областью определения {х :/г(х)<оо}, которая яв ляется границей области R :=/?-ехр<(%-ф0)л: R = \z = x + yi:к(x) G \ {0} = ^z = ехр{и/} = expire”'[: /г(гз1п(ф0 -ф))< гсоз(ф0 -ф)}. = к Пусть j I t £ f go i ~Нзо) уравнение 2п/ -периодической границы области R. Из того, L/ = f что точки kQ(t^ + ti, £0(f) + (f+2п)/еГ7? следует, что их образы х + к (х)/ := ^к0 (f) + ti)exp{(ф0 - ^ /}, хх + к (х,)/ := ^к0 (t) + (t + 2п)/)ехр{(ф0 - г^)/} е Г^. Расписывая эти равенства, получаем системы: fx = к0 (t) sin ф0 -1 cos ф0(хх = к0 (t + 2п) sin ф0 - (t + 2п) cos ф0 = х - 2п cos ф0 [Ar (х) = к0 (f) cos фу +1 sin ф0' [Ar (xt) = k0 (f + 2n) cos ф0 + (t + 2n) sin ф0 = к (x) + 2n sin ф0 То есть функция к^ удовлетворяет функциональному уравнению Аг(х-2псо5ф0) = А'(х) + 2п51пф0. Обозначим ^(х^Аг^ + ффо-х полунепрерывную сверху на ( +со) функцию. Так как кх (х - 2пcosф0) = к (х), то она (-2пcos ф0) -периодическая. „ tk0 (tA = /с(х)со5ф0 +хз1пф0 Решение первой системы { , х даёт уравнение границы области: [t = к(x)sinф0 -хcosф0 ГС = {ехр ^о (f) + ti^: t е (^ю, +x)j = ехр^/r(х)созфо + х sin ф0) + (/г (x)sin ф0 -хсо8ф0)/} :х е (-со,-ко ^ I у)г*нсгп -L Uk I у icinrh _ /х^ । л ।^.иь t^q i^ I **^ I^ J^'''Ч*о 4) Комплексную плоскость, в которой находятся М(С),С, обозначим cz; комплексную плоскость, в которой находятся R := In С (LnG), s (/?), обозначим cw ; наконец, комплексную плоскость, в которой находятся R :=R -ехр{(% -ф0)/{ обозначим г. Последняя задаётся полуне-ф0 W z ) прерывной сверху функцией к(х), а её мультипликатор содержит луч /п/2. vxeC„ вертикальная прямая Rei/ = х распадается на луч х + к (х)/ + (/п/21 {01) ^R и не пересекающуюся с R остав-Х ’ Фо Фо шуюся часть. Эта прямая поворотом на угол Фо - ^, преобразуется в прямую, которая состоит из луча (х + А'(х)/)ехр[(ф0 -%)/) + к \ {0} с R = In С и оставшейся части, не пересекающейся с /? =1пС. В свою очередь последняя прямая с помощью 2п/-периодического отображения х=ехр{и/{ преобразует в спирали z = г^9”0^ ехр{х//со5ф0{, проходящие через точки ехр{х//со5ф0{ единичной окружности и наматывающиеся на точки 0 и оо. При этом луч LcsiR преобразуется в спираль s = {exp{tcosф0 +t sinф0/: t > 01 = {r1+t9(p°' 1 с M(C), ko- V Фо/ Фо 1 ’ торая наматывается на 0, если |ф0 - п| < ^, и на оо, если |ф0| < ^. Поэтому область Gв первом случае представляет собой пучок спиралей с вершиной в нуле, а во втором — пучок с вершиной на бесконечности. Дополнение G' наоборот, в случае |ф0 - п| < ^ есть пучок спиралей с вершиной на бесконечности, а в случае |ф0| < ^ — ПУЧОК с вершиной в нуле. Отсюда, в частности, следует связность любого пересечения zxG'1 П^2(?'1, zx,z2 eG. Лемма доказана. Доказательство теоремы. Выберем по точке в двух компонентах связности вычета s((S) ^i е Кх, ^2 е Кг, и образуем линейный оператор [Lx](z|s?>±H^Wdl,+x,(o)infti,J- Г х(0^1п[^л FLll(z) = 0, FLi/l(z) = ln 2^ , FLi/nll(z)= [ vn 2dv = ^——- L J \ ' L J V / 7 ' L J V / J n -1 7"-1 z/^2 11 1VL>142 Его порождающая функция d (z) := In локально аналитическая на GG'1 = (М(С))' но мно гозначная, так как при обходе переменной годной из компонент Ki значение d^ изменится на слагаемое 2п/. Пусть теперь мультипликатор М (G) связный и * {1}. Согласно лемме 1 функция d (Q ана литическая в окрестности нуля и аналитически продолжается в каждую область z • G’NY, z eGn, no формуле Огтэртг*а лниз’эзти опио^идиипстц ^тпгп птнАлу/оима иэ x^l»। асi <-^i ди1ха5а i в идпиимочмис id a i ui и i i^aj^U/ izixCHrizi no GG* 1 = (м1. Пусть L eGG' \ L ^0, и для LLeG', zvz,eG G= — = — d^^kjj^z^ на z^G^.n d(^) = ^k^-.z^ на z2-С^1. По теореме единственности то- ГЛЭ П (( I — 1 к L 7 — z к z 7 1-1Э СВСЭиНМ ИНМПНЫРЫТР ГГГИПкППГП MUHWWTD3 । да и I ц । ~ f Zi — —~ f па ивяэнии kumi iumcm i с и i rudi i ui и мпижссi ва Z1*^N I I Z2 ' ^N ' В силу пункта 4 леммы 2 множество zxG,x W^G’"1 связное, и потому находится в этой связной компоненте. В частности, в точке £0 '2 или тА^—к^у Теорема доказана. ЗАМЕЧАНИЕ. В частном случае М((?) = (0,1) теорема была доказана в [6], а в случае, когда Gесть звёздная относительно начала координат область — в работе [10]. Заключение. Получено геометрическое описание односвязных областей G, имеющих связный мультипликатор. Этот класс областей характеризуется тем, что ядро любого ООД Гельфонда — Леонтьева из £а (G) порождается однозначной аналитической функцией.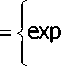
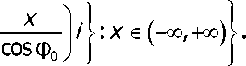
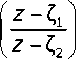
Список литературы О представлении операторов обобщённого дифференцирования Гельфонда - Леонтьева в односвязной области
- Гельфонд, А. О. Об одном обобщении ряда Фурье/А. О. Гельфонд, А. Ф. Леонтьев//Математический сборник. -1951. -Т. 29, № 3. -С. 477-500.
- Bieberbach, L. Analytische Fortsetzung/L. Bieberbach. -Berlin: Gottingen: Heidelberg: Springer-Verlag, 1955.
- Köthe, G. Dualitat in der Funktionentheorie/G. Köthe//J. reine angew. math. -1953. -Bd. 191. -S. 30-49.
- Коробейник, Ю. Ф. Об операторах обобщённого дифференцирования, применимых к любой аналитической функции/Ю. Ф. Коробейник//Известия АН СССР. Серия математическая. -1964. -Т. 28, № 4. -С. 833-854.
- Леонтьев, А. Ф. Обобщённые ряды экспонент/А. Ф. Леонтьев. -Москва: Наука, 1981. -320 с.
- Братищев, А. В. О представлении оператора обобщённого дифференцирования в одном классе односвязных областей/А. В. Братищев, А. В. Моржаков//Вестник Дон. гос. техн. ун-та. -2005. -Т. 5, № 4. -С. 481-490.
- Моржаков, А. В. Исследование операторов и операторных уравнений, порождённых обобщённым дифференцированием: автореф. дис. канд. физ.-мат. наук/А. В. Моржаков. -Ростов-на-Дону, 2008. -15 с.
- Братищев, А. В. О представлении линейных операторов, коммутирующих с дифференцированием, в односвязной области/А. В. Братищев//Вестник Дон. гос. техн. ун-та. -2014. -Т. 14, № 1. -С. 15-21.
- Братищев, А. В. Описание обобщённых преобразований Бореля, сохраняющих теорему Пойя/А. В. Братищев//Вестник Дон. гос. техн. ун-та. -2001. -Т. 1, № 1. -С. 79-89.
- Моржаков, А. В. О представлении оператора обобщённого дифференцирования в одном классе односвязных областей/А. В. Моржаков//Вестник Дон. гос. техн. ун-та. -2006. -Т. 6, № 1 (28). -С. 10-16.


