О представлении ортосимметрических билинейных операторов в векторных решетках

Если в векторной решетке зафиксировать положительно определенный биморфизм, то все регулярные ортосимметрические билинейные операторы представимы как суперпозиции линейных регулярных операторов с этим биморфизмом.

Цель настоящей заметки — установить один общий результат о представлении ор-тосимметрических билинейных операторов в векторных решетках: если зафиксировать положительно определенный биморфизм, то все регулярные ортосимметрические билинейные операторы представимы как суперпозиции линейных регулярных операторов с этим биморфизмом. Этот факт обобщает теорему 1 из [6] и лемму 4 из [7], но основан на ином подходе. Используются терминология и обозначения из [1]. Все рассматриваемые ниже векторные решетки считаются архимедовыми.

Возьмем векторные решетки E и F . Билинейный оператор b : E х E ^ F называют ортосимметрическим, если х ± у влечет b(x,y) = 0 для любых х, у G E , см. [3, 5, 6]. Для положительного билинейного оператора b (b(x, у) >  0 при х, у G E + ) в силу неравенства | b(x,y) | 6 b( | x | , | у | ) ортосимметричность равносильна справедливости импликации х Л у = 0 ^ b(x, у) = 0 для всех х, у G E . Скажем, что оператор b положительно полуопределен, если b(x, х) > 0 для всех х G E. Если же, сверх того, из b(x, х) = 0 следует х = 0, то b будем называть положительно определенным. Множество всех орто-симметрических регулярных билинейных операторов из E × E и F обозначим символом BL or (E, E ; F ). Пусть L r (E, F ) — пространство всех регулярных линейных операторов из E в F . Ясно, что BL or (E, E; G) и L r (E,F ) — упорядоченные векторные пространства, в каждом из которых конусом положительных элементов служит множество положительных операторов. Теперь мы сможем сформулировать основной результат настоящей заметки.

Теорема. Пусть E , F и G — векторные решетки, причем G полна относительно схо димости с регулятором. Пусть (• , •} : E x E ^ F — положительно определенный решеточный биморфизм, причем подрешетка в F, порожденная множеством {{ х,у ) : х,у G E } , совпадает с F . Тогда для любого ортосимметрического регулярного билинейного оператора b : E х E ^ G — существует и притом единственный регулярный линейный оператор Ф := Фь : F ^ G такой, что

Ь ( х, у) = Фb( h x, У i ) (х, у G E ).

(с) 2005 Кусраев А. Г.

Сопоставление b ^ Фь осуществляет изоморфизм упорядоченных векторных пространств BL or (E, E; G) и L r (F, G).

Доказательству предпошлем несколько вспомогательных утверждений.

Лемма 1. Решеточный биморфизм b : E х E ^ F ортосимметричен в том и только том случае, если он положительно полуопределен. В этом случае b(x, y) = b(y, x) для всех x, y E E .

C Пусть b — положительно полуопределенный решеточный биморфизм. Возьмем x,y E E и положим a := b(x,x), в : = b(y, y) и y : = b(x, у) + b(y,x). В силу положительной полуопределенности a + в - Y = b(x - У, x - У) > 0. Если x Л у = 0, то b(x, у) > 0 и, поскольку b(x, • ) и b(>x) — решеточные гомоморфизмы, можем написать a Л b(x, у) = b(x, x Л у) = 0 и a Л b(y, x) = b(x Л у, x) = 0. Тем самым, a A y и аналогично в A Y. Но тогда (a + в ) A Y, и из неравенства a + в - Y > 0 вытекает y = 0, стало быть, b(x, у) = Ь(у, x) = 0. Обратное верно для любого положительного b, так как из ортосимметричности b вытекает b(x, x) = b(x ⁺ ,x ⁺ ) + b(x - , x ^- ). Последнее утверждение леммы следует из [6; следствие 2]. B

Лемма 2. Пусть Q — компактное хаусдорово топологическое пространство и E — равномерно плотная подрешетка в C(Q). Пусть G — векторная решетка, а G — ее порядковое пополнение. Для любого положительного ортосимметрического билинейного оператора b : E х E ^ G существует и притом единственная положительная счетно аддитивная квазирегулярная борелевская мера на Q х Q со значениями в G такая, что b(x,y) = У x(s)y(t) d^(s,t) (x,y E E) QxQ и p(Q х Q \ A) = 0, где A := {(q, q) : q E Q} — диагональ Q х Q.

C Существование меры µ, обеспечивающей указанное представление, показано в [2; предложение 1.7]. Используя лемму Урысона [4; теорема 1.5.10], можно показать, что p(K ) = 0 для любого компакта K C Q x Q \ A, см. [9; пример 2.3]. Так как Q х Q \ A открыто, то остается заметить, что в силу квазирегулярности ^ имеем ^(Q х Q \ A) = sup { ^(K) : K C Q х Q A, K — компакт } = 0. B

Лемма 3. Пусть линейный положительный оператор T : E 0 E ^ G таков, что билинейный оператор T 0 : E х E ^ G ортосимметричен. Если Tu >  0 для некоторого 0 6 u E E 0 E, то существует элемент e E E такой, что 0 < e 0 e 6 u.

C В силу свойств тензорного произведения E 0 E (см. [8; пункт (iii) теоремы 4.2]) существует eg E E+, для которого u 6 eg 0eg. Пусть Eg — порядковый идеал в E, порожденный элементом eg. Тогда Eg 0 Eg — подрешетка в E 0 E, порожденная множеством Eg 0 Eg (см. [8; следствие 4.5]), и если Tg — ограничение оператора T на Eg 0 Eg, то билинейный оператор bg := Tg0 : Eg х Eg ^ G положителен и ортосимметричен. В силу теоремы Крейнов — Какутани Eg можно считать равномерно плотной подрешеткой решетки C(Q) для некоторого компактного хаусдорфова пространства Q, причем Eg содержит константы и разделяет точки. В силу леммы 2 существует счетно аддитивная положительная квазирегулярная борелевская мера µ со значениями в порядковом пополнении G такая, что bg(x,y)= j x(s)y(t) d^(s,t) (x,y E Eg). QxQ

Более того, .(Q х Q \ А) = 0. Если функция u Е Е о 0 Е о обращается в нуль на А, то

Tu

j ud. =

[ ud. ₊ /

ud. = 0,

Q x Q       Q x Q \ A       A

что противоречит условию Tu >  0. Тем самым, u(q,q) > 0 для некоторого q Е Q. Подберем е >  0 так, что открытое множество { (p,p ⁰ ) Е Q х Q : u(p,p') > е } содержало в себе прямоугольник V × V для некоторой открытой окрестности V точки q . По лемме Урысона [4; теорема 1.5.10] существует непрерывная функция х : Q ^ [0,1] такая, что x(q) = 1 и х(р) = 0 для всех p / V. Ясно, что ех 0 х 6 u. Так как Е о равномерно плотна в C (Q), то можно подобрать такую функцию e i Е Ео, что | e i — ех + 1 1| 6 41. Тогда е(х — 4 1) 6 e 1 6 е(х — 4 1) 6 ех и для e := e + Е Е о будет 0 < e 6 ех, так как e 1 (q) = 4 = e(q). Тем самым, 0 < e 0 e 6 u. B

Приступим теперь к доказательству сформулированной теоремы.

C По теореме Д. Фремлина [8; пункт (i) теоремы 4.2] существует решеточный гомоморфизм ф : Е 0 Е ^ F такой, что h^ , -i = ф 0 . Так как ф(Е 0 Е ) — подрешетка в F и содержит все элементы вида h x,y i , то F = ф(Е 0 Е ). Возьмем ортосимметричес-кий положительный билинейный оператор b : Е х Е ^ G. В силу свойств тензорного произведения по Д. Фремлину [8; теорема 5.3] существу е т и притом единственный положительный оператор T : Е 0 Е ^ G, для которого T 0 = b. Если подберем линейный оператор Ф : F ^ G, для которого T = Ф ◦ ф, то диаграмма

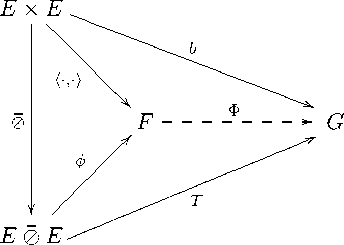
коммутативна. В частности, b = Ф oh- , -i . Если f Е F + , то в силу сюръективности ф имеем f = ф(u) для некоторого 0 6 u Е Е 0 Е , поэтому Ф(f) = Tu >  0, т. е. Ф положителен. Единственность Ф вытекает из равенства Ф ◦ ф = T . Итак, для существования Ф с указанными свойствами достаточно установить, что кег(ф) С ker(T). Так как ф — решеточный гомоморфизм, то u Е кег(ф) в том и только в том случае, если | u | Е кег(ф), поэтому можно ограничиться случаем положительного u Е Е 0 Е. Если 0 6 u / ker(T), то по лемме 3 можно подобрать 0 < e Е Е так, что e 0 e 6 u. Но тогда 0 = ф(u) > ф(e 0 e) = h e, e i , что противоречит положительной определенности h- , -i . Итак, кег(ф) С ker(T), что и требовалось.

Если теперь b — ортосимметрический регулярный билинейный оператор, то b = b 1 — b 2 для некоторых 0 6 b i ,b 2 Е BL or (Е,Е ; G). Согласно доказанному существует пара положительных операторов Ф 1 , Ф 2 Е L r (F, G) такая, что b k = Ф к ◦ h- , -i . Для Ф := Ф 1 — Ф 2 будет Ф Е L r (F, G) и b = Ф ◦h^ , •i . Единственность Ф видна из того, что Ф ◦ ф = T 1 — T 2 , где положительные операторы T i , T 2 Е L r (Е 0 Е, G) однозначно определяются равенствами T k 0 = b k (k = 1, 2). B

Пусть L обозначает линейную оболочку множества {h x,y^ : x, y G E } , а векторную решетку F := ф(E 0 E ) обозначим символом h E' i .

Следствие 1. Справедливы следующие утверждения:

• (1)    L плотно в h E i в том смысле, что для любых u G h E' i и е >  0 существуют e o G E и v G L такие, что | u — v | 6 e h e o , e o i ;

• (2)    если 0 < u G h E' i , то существует элемент 0 < e G E, для которого h e, e i 6 u.

C Утверждение (1) следует из [8; пункт (iii) теоремы 4.2], а (2) из леммы 3. B

Следствие 2. Пусть A — точная f -алгебра, E — произвольная векторная подрешетка в A, F — произвольная векторная подрешетка в A, порожденная множеством { xy : x,y G E } , G — (г)-полная векторная решетка. Тогда для любого положительного ортосимметрического билинейного оператора b : E х E ^ G существует единственный положительный оператор Фь : F ^ G такой, что b(x,y) = Фь(ху) (x,y G E ) .

C Умножение в точной f -алгебре является положительно определенным решеточным биморфизмом. Поэтому достаточно взять в основной теореме h x,y i := xy (x,y G E). B

Можно убрать требование (г)-полноты G из условия следствия 2, но тогда Фь можно определить только на линейной оболочке L множества произведений { xy : x, y G E } , см. [7; лемма 4]. Если же E (г)-полна, то F совпадает с L, см. [7; лемма 8].

Пусть P и Q — экстремальные компакты, σ — непрерывное отображение открытозамкнутого множества P o С P в Q, причем считаем, что a(P o ) плотно в Q. Пусть E — подрешетка в C ^ (P ) и для e G E обозначим символом a * e функцию из C ^ (P ) определяемую как e(a(p)) при p G P o и обращающуюся в нуль на P \ P o . Зафиксируем слабую порядковую единицу w G C ^ (P ) и обозначим буквой F подрешетку в C ^ (P ), порожденную множеством { wa * (e)a * (f) : e, f G E } .

Следствие 3. Для любого регулярного ортосимметрического оператора b : E х E ^ G существует единственный регулярный линейный оператор Фь : F ^ G такой, что b(e,f) = Фь^о^^о^)) (e,f G E).

Сопоставление b ^ Фь является изоморфизмом упорядоченных векторных пространств BL or (E,E; G) и L r (F,G).

C Нужно применить основную теорему к биморфизму h e, f i := wa * (e)a * (f). Положительная определенность обеспечивается тем, что a(P o ) плотно в Q и w обращается в нуль лишь на нигде не плотном множестве. B