О представлении в виде пространств кёте пространств голоморфных функций

Семeну Самсоновичу Кутателадзе к его шестидесятилетию

В статье изучаются свойства разложений по системе мономов голоморфных функций, определенных на пространствах К¨ете — Фреше. Дается представление пространств голоморфных функций на ядерных пространствах К¨ете — Фреше с топологией компактной сходимости в виде (неметризу-емых) пространств К¨ете.

В работах [1–4] исследовались пространства голоморфных отображений между локально выпуклыми пространствами, что относится к так называемой бесконечномерной голоморфности. Сначала в [1] было показано, что в пространствах C-значных голоморфных функций на совершенно (fully) ядерных пространствах с базисом система мономов (z m ) образует абсолютный базис (относительно компактно открытой топологии). Затем в [2, 3] для пространства голоморфных функций на монтелевском пространстве E получены некоторые результаты в противоположном направлении, т. е. из абсолютной базисности системы мономов выводилось свойство ядерности пространства E (и E _β ⁰ ).

В [4], в частности, показано, что система мономов образует равностепенно непрерывный безусловный базис (Шаудера) в пространстве голоморфных функций на пространстве l 1 (относительно топологии τ 0 равномерной сходимости на компактных множествах).

В настоящей работе рассматриваются пространства H(Е,т о ) C-значных голоморфных функций на пространствах К¨ете — Фреше и для этих пространств при условии ядерности пространства Кете E приводится реализация H(Е,т о ) в виде пространства К¨ете с матрицей К¨ете, элементы которой выражаются через элементы аналогичной матрицы представления для E. В доказательстве совершенствуется техника работ [1–4]. В частности, уточняются и снабжаются более доступными ссылками) оценки мономальных разложений из [1, 3].

Заметим, что случай p = го , частично рассмотренный в [1], исследуется с привлечением более тонких, по сравнению с [1], оценок норм случайных тригонометрических полиномов из [5].

Пусть E и F — локально выпуклые пространства над полем C, U — открытое подмножество E .

Определение [3]. Функцию f : U ^ F называют голоморфной, если она непрерывна и для любых u G U , v G E и ^ G F ⁰ отображение C 3 А ^ ^(f (u + Av)) голоморфно как функция одного комплексного переменного на ее области определения.

Бесконечномерной голоморфностью называют исследование голоморфных отображений между локально выпуклыми пространствами. Эта область анализа особенно быстро расширяется в последние десятилетия (библиографию см., например, в [1–4]).

Сосредоточим внимание на C-значных голоморфных функциях. Множество всех C-значных голоморфных функций на U обычно обозначают H(U ).

Пусть А : E —» E n : = E х • • • х E обозначает диагональное отображение, т. е.

n

A(z) = (z,...,z). Отображение вида P = L о А, где L есть n-линейное отображение | {z }

| {z } n на E n , называют п-однородным полиномом на E . Через P ( n E) обозначают линейное пространство всех непрерывных n -однородных полиномов на E . Полиномами называют конечные суммы однородных полиномов.

Если ^ G E 0 , то y ⁿ £ P ( n E). Элементы алгебры, порождаемой y ⁿ , п £ N и у £ E 0 называются полиномами конечного типа .

Рассмотрим теперь локально выпуклое пространство E с базисом (е _п ) П=р Символ N ^{( n )} обозначает множество финитных последовательностей целых чисел, т. е. m £ N ^{( n )} означает, что m = (m i , m 2 ,..., m n , ...) и m i = 0 для всех i >  i _m .

Мономом z ^m (относительно базиса (е _п ) П =1 ) называют отображение

^{X ∞}        m 1 m 2      m n

Ту znen 1 z1     z2     * * * zn     ..., n=1

где подразумевается a ⁰ = 1 для любого a £ R. Каждый моном определяет элемент P ( ^|m| E), где | m | = P i m i | . С использованием полиномов можно получить разложение в ряд голоморфной функции (аналог разложения в ряд Тейлора).

Отображение f : U ^ C голоморфно тогда и только тогда, когда для каждого u £ U существует последовательность (Р _п , _и ) П =о , P n,u £ P ( n E) для всех п, такая, что

∞ f (u + z) = ^Pn,u(z)                              (1)

n =0

для всех z из некоторой окрестности нуля, и ряд сходится равномерно к f на некоторой окрестности нуля. Представление (1) называют разложением f в ряд Тейлора в точке u. Согласно интегральной формуле Коши (размерности 1),

_ 1 Г f(u + Az)     £ dnf n,u   2ni /    An+1         n! dzn u^

|A= для всех u £ U, n £ N, z £ E и достаточно малом 6 = 6(u).

Естественной областью сходимости (1) является уравновешенное подмножество E , и когда U само уравновешенно, тейлоровское разложение в нуле сходится к функции во всех точках U .

В частности, если E — пространство Фреше, (^ _п ) П =1 — последовательность в E 0 , то

∞ f = ^>n £ H(E)

n =1

тогда и только тогда, когда ^п ^ 0 при п ^ го равномерно на компактных подмноже-∞ ствах E . В этом случае   ϕnn — разложение в ряд Тэйлора функции f в нуле.

n =1

Если E — локально выпуклое пространство с базисом (en)^! и f Е H(E), то для каждого m Е N(n) определяются по f мономиальные коэффициенты (am)mG,(N), как и в конечномерном случае, по формулам am

1 с    П (П 1 ,П 2 ,...,П г , 0,...h _л _д m l f^

(2ni) r J •••] n m i ⁺ⁱ n m 2 ⁺ⁱ ... n m r +1 d ^{n i} '" dⁿ r     dz m ^{(0) ,}

T T где r = r(m) таково, что mi = 0 для i > r, множество T определяется формулой

T=

S 52 n i e i ;

I i=i

In i l = a i > 0 для i = 1, 2,.

.,r

и dn i ... dn r — мера Лебега на T . Коэффициенты (a m ) _{m G} , ( N ) не зависят от r и положительных чисел a i , i = 1, 2,..., r. Таким образом, получается мономиальное разложение f

Е mG,(N)

a m z ^m .

Так как множество индексов в сумме (2) неупорядочено, приходится сначала рассматривать ее безусловную или абсолютную сходимости. При рассмотрении мономиальных разложений вводится несколько видов сходимостей и топологий на пространствах голоморфных функций. Наиболее часто используется компактно открытая топология т д .

Для мономиальных разложений обычно предполагается любо безусловная, либо абсолютная сходимость. Естественной областью такого разложения является полидиск.

Пусть E — ядерное пространство Фреше с базисом Шаудера. Тогда E изоморфно пространству Кете с абсолютным базисом ортов. Можно сразу считать E = l i [a _r (n)] и предполагать условие ядерности в виде (см. [6]):

∞

X n=i

a r (n) a r +i (n)

< ∞ .

Для элементов E введем новые обозначения: k (z n ) n =i k r = ^2_n | z _n | a _r (n), z = (z _n ) Е E . Пусть V — открытый полидиск в E , т. е. V = { (z n ) n =i Е E : sup n | z n | a(n) < 1 } , где (a(n)) n =i — последовательность неотрицательных чисел с оценками для некоторых c >  0 и r(0) Е N, a(n) >  ca _r(g) (n), n Е N. Если K — компактное подмножество V, то можно указать последовательность положительных чисел (a n ) n =_i таких, что K С K = © (z _n ) n =_i Е E : sup n | z _n | a _n 6 1 } , где K — компактный полидиск в V.

В работе [1] было показано, что если V — открытый полидиск в ядерном пространстве Кете E = l i [a _r (n)], то мономы образуют абсолютный базис Кете в (H(V), т д ). В частности, в пространстве (H(Е),т д ) мономы образуют абсолютный базис Кете, если E — ядерное пространство Фреше с базисом. Докажем некоторое обобщение результата из [2].

Теорема. В пространстве (H(X), тд) голоморфных функций, заданных на пространстве Кете X = lp[ar(n)], 1 6 p 6 го, система мономов (zm)mGN(N) является абсолютным базисом К¨ете в том и только том случае, когда пространство X ядерно. Пространство (H(X), тд) в этих случаях изоморфно пространству Кёте li [a(m, (r(n)))] mGN(N),(r(n))GS = li

[ a m i) (l)--a mkS ) ( ^k (m))J m G ,,,^'

где S —совокупность всех последовательностей натуральных чисел r(n) с lim r(n) = го . n →∞

C Чтобы получить представление пространства аналитических функций, определенных на пространстве Кете E = l p [a _r (n)], 1 6 p <  го , в виде пространства Кете, подсчитаем нормы элементов базиса (мономов). Для этого воспользуемся свойствами фундаментальных систем ограниченных и компактных множеств. Предположим в E наличие монотонной системы полунорм | • | _r 6 ^ Г | • | r +i , r G N, и тогда каждое ограниченное множество содержится в ограниченном p-эллипсоиде вида

C^z = (z n ) n =i : XX I z n i p 6 1} ,

C> 0,

где λ n описаны выше как λ αn , а каждое компактное множество содержится в компактном p-эллипсоиде (p = 1)

K ( r ( n )) = C

^ ^z = (z n^n^i

X | ^Z n |4_H^{( n ) 6} 4 , n

C> 0,

где (r(n)) — последовательность натуральных индексов с lim n .^ r(n) = го . Соответствующие компактным p -эллипсоидам нормы будем обозначать

| z | ₍ ^p _r(n)) =        | z n | ^p a ₍ ^p _r(n)) ( n ) ,

n kfk(r(n)) = suP {|f (z)| : z G K(r(n))} .

Матрицу Кете пространства (H(U), то) образуют нормы мономов ||zmk(r(n)), где m G N(n) и индекс (r(n)) пробегает все последовательности натуральных чисел с limn .^ r(n) = го. Для подсчета указанных норм мономов воспользуемся известным неравенством между средним геометрическим и средним арифметическим ai • ... • an 6 (

P i a i + • • • + P n a n

p i + . . . p n

^ Р 1 + +P n

,

где a i >  0, p k >  0, причем равенство будет только в том случае, когда все a i равны. Это неравенство в эквивалентной форме прямо следует из неравенства Йенсена для выпуклой функции. Применение неравенства между средним геометрическим и средним арифметическим дает оценку

। zi pm o pm ; (1) • ... • a :m;m)) (^k(m))

m ^m

k ( m )

= п i=1

| Z i | p a P ( i ) (i) '

m i

Г Е i =i | Z i | p a P ( i ) (i) | m |

| m |

p | m | ^{| Z |} ( r ( n )) | m | | m | ^.

Здесь для финитной последовательности m = (mi,..., mk(m)) из N(n) считаем k(m) максимальным индексом, для которого mk(m) = 0, а среди mi, i < k(m), могут быть и равные нулю. Вводя обозначение перепишем полученную оценку для нормы монома

m jmiimij a(m, (r(n)))-

С другой стороны, подсчитывая значение монома на элементе

^k(m)     _m ¹

Zo =^2 ---Г^----ei, где e = (Sij)j=i> i E N i=i |m| p ar(i)(i)

^{| z} 0 ^| ( r ( n )) =

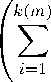
p m i ^a r(i) ^{| m |} a p ( i )

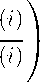
1 ^p

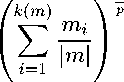
= 1,

получим

k ( m )

z m = П — i =i | m |

m i P m _i

m i p a m ) (i)

m m _p

I I m ¹ | m | ^p

a ( m, ( r ( n ))) ,

а значит,

mp kzmk(r(n)) = (imimT) am

,^{( r ( n )))},

m E N ^{( n )} .

Таким образом, с точностью до «диагонального» преобразования, искомая матрица К¨ете имеет вид

[a⁽m, ^{( r ( n )))}] m e N ( N ) , ( r ( n )) e S =

,

»mi) (1) -гокК» (k(m)) «<«>,,»„ l r(i)            i(k(m))           J m€NiN),(r(n))€S где S — совокупность всех последовательностей натуральных чисел r(n) с lim r(n) = го.

n →∞

Рассмотрим теперь пространство H(E ) аналитических функций на пространстве Кете E = l i [a r (n)] и будем предполагать, что система мономов образует в нем абсолютный базис, более точно, p-абсолютный базис Кете (р = 1). Это значит, что для любого абсолютно выпуклого компактного множества K существуют константа C >  0 и компактное абсолютно выпуклое множество K такие, что

52 | c m | sup |z ^m | 6 C sup I 52 C m Z m

m∈L    z∈K        z∈K m∈L для любого набора чисел (am)mGN(N) и каждого конечного множества L С N(n).

Считаем систему полунорм ( | • | _r ), определяющую топологию E , монотонной с неравенствами | • | _r 6 7171 • |r +i , r E N. В этом случае можно рассматривать равномерную сходимость в H(E) только на компактных множествах вида

K ( r ( n )) = C

। Z = (Z n )

^| z ^| ( pr ( n ))

∞

= X ^{| z} n ^{|P a} p ( n ) ^{( n ) 6 1}

n =i

,

где C >  0 и lim n .^ r(n) = го . С учетом найденных выше значений ||z m k ( r ( n )) перепишем (3) в следующем виде:

m ^m

52 ^{|С т |}ыы^{a (}m^{( r ( n )))}

mENM     1 1

6 C sup

< X c m a(m, (s(n)))w ^m

I me N ( ^N)

k w k l _p

∞

= ЕК| ^Р 6 1

n =1

,

где (c m ) m e N ( N ) может быть любым набором коэффициентов мономиального разложения функции f G H(E ). Обозначив c _m a(m, (s(n)) = d m , m E N ^{( n )} , приходим к виду

^X I d m ' a^m; ^L 6 C supf ^X d- m >  M, p 6 4'

meWO     a¹™, < ^s ( ”)» ^{| m | 1} ” ¹          I ,„да              p J

Так как (3) справедливо для полиномов, в частности, n -однородных полиномов, посредством рассмотрения в приведенных неравенствах конечных сумм с | m | = 2 покажем ядерность пространства К¨ете — Фреше E .

Рассмотрение конечных сумм в (3) с | m | =2 и оценками 4 6 | m | m | 6 1 для этого случая приводит к условию

X .a mi ) (i j Ья

X |aij1 m4    mj ( Л 6 C SUP i,j=1       ar(ii) (i)ar(j) (j)

{n X i,j=1

,j =1

a ij n i n j ^{: max}

| η i |

(C = 4C, m i + m j = 2) для любой симметрической матрицы ((a ij ))^- =i с | a ij | 6 1 при любом n ∈ N.

Для оценки правой части последнего неравенства воспользуемся следующим следствием теоремы 3 главы VI из [5].

Лемма [5]. Если заданы комплексные числа aij, |aij | 6 1, i, j = 1, 2,... ,n, то существует такой набор знаков + и —, что n

sup t1,t2,...,tn

У ±a k,j e^{t( kt} k j ) k,j =1

/ n               \ 2

< C( n 52 |a kj | 2 log2n I k,j =1

6 Cn 2 log 2n,

где C — некоторая абсолютная постоянная.

Соединяя последние неравенства, получаем

/       . as(i)(i)\ n min ---—  6

у ^{16 i} 6 ⁿ a r(i) ^{( i )} у

n

X

i =1

a s ( i ) (i) a r ( i ) ( ⁱ )

—   3

6 CCn 2 log 2n,

т. е.

a s ( i ) ( ⁱ )

min --— i6i6n ar(i) (i)

log2n

6 D i n 4

Можно повторить достаточное число k >  5 раз процедуру выбора для последовательности (s(n)) n =i в условии (3) и проведенные оценки, чтобы получить последовательность ( s (n))n‘ =i , для которой сходится ряд

∞

X

n =i

^a e( n ) ^{( n )} a r ( n ) ^{( n )}

6 D

∞

n =i

(log 2n) ⁵

n 4

< + го .

Но найти для любой последовательности (г(п)) П=1 с lim n _?^ r(n) = го другую такую последовательность ( е (п)) П =₁ с lim n _?^ e (n) = го , чтобы сходился указанный ряд, можно лишь в случае, когда для E справедливо условие ядерности Гротендика — Пича (см., например, [6]):

∞

E a r (n)

----< +го- n=1 as(r)(n)

Предположим, что условие ядерности E не выполняется, т. е. существует r(0) G N такое, что при любом s ∈ N ряд

∞

X

n =1

a r (0) (n) a s (n)

расходится. Тогда выбрав, согласно расходимости соответствующих рядов, последовательность натуральных индексов (nk)^=i так, чтобы nk+1-1 X n=nk

ar(0)(n) > 2k,   k = 1, 2,..., ar(0)+k (n)

построим последовательность (r(n)) ^ =i следующим образом:

r(n) = r(0), n 6 n ₁ ,   r(n) = r(0) + k, n k < n 6 n k +1 , k = 1, 2,...

Теперь для любой последовательности (s(n)), у которой limn ?^ s(n) = 0, с некоторого номера m будет s(n) > r(0) и для nk > M выполняется так что ряд

n k+1 ^{- 1}

X

П=П к

^a s(n) ^{( n )} a r(0)+k ^{( n )}

>

ⁿ k+1 ^{- 1}

X

n = n k

^a r (0) ^{( n )} a r(0)+k ^{( n )}

> 2 ^k ,

∞

X

n =1

asH(n) ^a r ( n ) ^{( n )}

расходится. Полученное противоречие означает, что условие ядерности для пространства Кете E = l ₁ [a _r (n)] должно быть выполнено, если мономы образуют абсолютный базис Кете в H (E). Оставшаяся часть утверждения теоремы следует из упоминавшегося результата работы [1] (см. и [3]). B

По сравнению с результатом из [2, 3] здесь не накладывается требование монтелевости E и добавлен случай p = 1.

Было бы интересно исследовать характер базисности мономов в случае пространств аналитических функций на пространствах К¨ете без условия ядерности. Приведенные оценки норм мономов и часть рассуждений остаются справедливыми и в этом случае.