О приближенном вычислении интегралов типа коши

В формуле (И) Ф(() = ttpYY

Коэффициенты A*_a^YY (^ ⁼ 0,1,2) легко вычисляются и имеют вид:

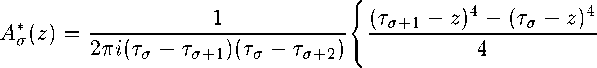
+ 1------------------ ^z - t₀ + z - Н + z - (₂ + z - Phi + z - т„^

^X-^-YVa-zY ^ _ ^ _ ^ ^_ ^ _ ^ + ^ _ ^ _ ^

+ Y - thi + z- т_а+2М -to + z-K+z-^ + ^z- T„MY - T_ff+2)]

+ (^+1 - tY [(Z - toY^ - KYz - (₂) + (z- T.+ i + г - t_ct+Y

X ((z - KHz - tH + ^Z- toHz - tH + ^Z- toHz - H))

+ (z - to + Z - t-_k + z - t₂Hz - t_ct+1)(z - T_ff+2)]

+ У - T^ + l + Z - T_{ct +} 2H^z - toHz - tiHz - 1₂) + ((^ - tiHz - 1₂)

+ (г - ф)(г - 1₂) + Y - toHz - txY^z - t_ct+iHz - t^+2)] ln^+1—^ J Ту- z

+ (z - toHz - tlHz - t₂Hz - T_{ct +} 1Hz - T^+2)-- L                                             J \ t^+i - z

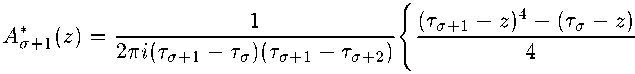
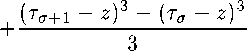
+ Z - ty + Z - t₂ + Z - T_a

z -t0

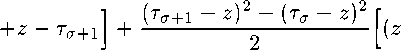
+ (z - t₀)(z - ti) + (z - т_а + z - t_ct+2)(z - to + Z - ti + z - t₂)

)(z - 7„₊₂)j + (7^1 - 7^) [(z - t₀)(z - ti^z - t^

+ (z - т_а ! z - 7_{)((z -} t^Z - 0) + ^z - to^z - t₂)

+ (z - t₀)(z - t^) + (z - to + Z - H + z - t₂)(z - r_a)(z - 7„₊₂)j + (z - T_a + z - t_ct+2^z - to^z - t^z - t₂) + ((z - t^z - t₂)

+ (z - to)(z - t₂) + (z- to)(z - t^^z - T_a^z - 7-^+2)] In A±1--- A T_CT - Z

+ (z - toHz - t^Z - t₂^Z - T_a)(z - 7_{a + 2})--- 1--

L                                            J у ^H-l Z Ta z д *      = ____________1J A-I - z)4 - (t^ - z)4

^a+2 2тгг(т_т+2 - 7_(Т)(7_(т+2 - T_ff+1) I             4

(7_a+i — A — (or — zV Г

+ ---------------------^z - to + Z - ti + z - t₂ + z - T^+1

1          — zA² —    — zA² г

+3 - T,] +             ---A ^ _ t^_z _ t^ ₊ ^_z_ t^z -1₂^

+ (г - to^z - ^1) + (г - To-₊1 + z - tZ)Iz - t₀ + z - ti + z - t₂^

+ (z - T.Kz - T.+ x)] + (7.,+! - 7.) [(г - toHz - M(z - t₂)

+ (z - 7. + Z - 7,+x) ((z -tl)(z- t₂) + (z- to)(z - t₂)

+ (z - t₀)(z - #1)) + (z - to + z - h + Z - t₂^Z - 7^)(z - 7_ff+l)j

+ (z - 7^ + Z - 7_(T+l)(z - to^Z - ^i)(z - ^₂) + ((z - ^l)(z - ^₂)

+ (z - to^Z - ^₂) + (z - to^Z - ^l))(z - 7_(T)(z - 7^ + 1)] In A±1---^

+ (Z - toHz - tl^Z - t^^Z - 7_(T)(Z - 7^ + 1)

1             1

--h --------

7^ + 1 - Z T_o- Z

Оценим погрешность квадратурной формулы (11). Нетрудно убедиться, что она имеет вид

\Rn‘2^tp;z)\ = О , так как если z близко к контуру L, то to = Н = z.

Аналогично строятся квадратурные формулы и для четвертого интеграла в формулах (1):

кН²) Ri Ф(ф,^,^₂) + 52 (^Г(^г)^ф(^т<7,Ф,^1,^2) + А^^Ф^+ьфЛЛ)

7 = 0

+ ^Г+2(г)Ф(т<т+2,Ф,^1,^2)),

где

₌ ___________1___________/ (Ат+1 - ^)³ - (^ - г)³ 2тп(т₍₇-т₍₇₊₁)(т₍₇-т₍₇₊₂Ц          3

+ ^±1---L_—^--fL ^ _ t₀ + z - К + z - t₂ + z - T^+1 +3 - т_стЦ + (т^ - tJ [(г - KHz - K) + (г - KHz - tn +(z - toHz - K) + (z- t_ct+i + z- T_a+2Hz -K + z-K + z-K)

+ (z - T.^ - W)] + [(3 - toHz - KHz - tH + (z- T. _{+ 1} Kz - т^Н^К - KHz - <2) + (^ - Ф)(г - tn + (z - KHz - ti))

- KHz - T^+H^z - r„₊₂)j

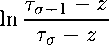
+ (z - t0 + z - К + z

+ (г - т_а+1 + z - T_a+2Hz - KH^Z - KH^Z - Ы + ((z - KHz - ^2)

+ ^z - KHz - tH + (г - KHz - li))(^ - T_ct+1Hz - T_ct+2

X

1             1

--1--

TcVv - z Ta - z

+ (z - toHz - tlHz - t₂Hz - T^+1)

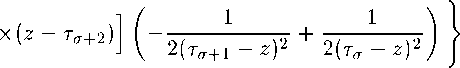
/ x ₌ _____________1_____________/ (r<7 + l - zH - (^ - zH

^,t+1      2тгг(т₍₇₊1 - T^))^! - T^+H (            3

+ -^y--11_—^--^L [_г _ to + z - ti + z - t₂ + z - T_a

+Z - т_стЦ + (т.,+1 - тП [(з - KHz - tn + (^ - toHz - tH

• + (z - toHz - tn + (z - T_a + z - T_ff+2Hz -to+z-K+z-tH

p^z - T.Hz - т,₊₂)] + [(г - toHz - KHz - <2) + (z - т_а

• -Vz - T_tr+2)((z - tiHz - tn + (z - toHz - tH + (z - to)(z - ti))

+ n - to + Z - К + z - kHz - T_CTHz - T_ff+2)1 In ^±1---

J T_c- z

+ (^ - T_a + z - t_ct+2Hz - KHz - t-kHz - tH + ((z - t-_kHz - tH

+ (z - to^z - <₂) + (^ - to^z - Д))(з - т_а^г - T_ff+2)j

X (----- + ^—) + Vz-t^z-t-^z-t^z-T^ \ ^_| - z T_a-z) L

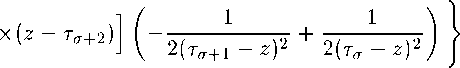
______________1______________f - г)³ - Ут_с - г)³ 2тгг(т₍₇₊₂ - т_(Т)(т_(т+2 - т^+i) |            3

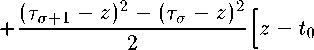
+ z - ti + z - t2 + z - TCT

Xz - T^ + ij + (t^+1 - tJ |_(z - ti)(z - t₂) + (^ - to)(z - t₂)

+ (z - to)(z - it) + (z - T_CT + z - T_ff+1)(z -to + z-ti + z-t^ + (z - T.Hz - T^j] + [(г - to^z - Д)(г - t₂) +(z-T„ Xz - т₍₇₊1)((г - t^z - t₂) + U -

+ (z -tg + z-ti+z - t2)(z - tct)(z - T^+Jj x (------ +       ) + b - to)^ - ^1)(^ - ^2)(^ - T.)

\ T^+1 - z T_a-Z) L

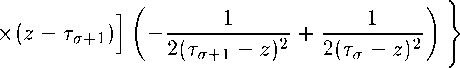
Для остаточного члена имеем

_D z x 1 \- (t - to^t - ti^t - ^2)г_П(Т(у2ДД₀Д1Д₂)

R^' z) = 2^2^--------------------dt a=0                     v '

-2тгг^ / г^(уДДоД1Д2)^+ 2?г.

Е ⁺   Г T^^Vip-, t, ФД1Д2)

<г=от ;

to^z - ^2)

‘''^-^^ /

1^ММд!11М^ + (г_^0)

‘*-^^„ /

T^^t^to^!,^

Для формулы (12) также справедлива оценка

\Rn3^; z)\ - О

• §2. Вычисление компонентов напряжения основной смешанной задачи плоской теории упругости

Пусть упругое тело занимает на плоскости z = ж + iy конечную область S, ограниченную простым замкнутым гладким контуром L (см [4]).

Основные уравнения плоской теории упругости при отсутствии объемных сил сво-

дятся к следующим: ЭХх   ЭХу       ЭУХ   дУ.„ ----^- = 0  —--- = 0 ох    оу       ох   оу Oil                      Ol) Xx = A0 + 2/z——, Уу = A0 + 2/z——,                   (13) Эх              Эх v         / dv  du\ Xy — Yx — /z ---4 — , \Эх Эу / где Хж,Уу,Ху = Ух — компоненты напряжения, u,v — компоненты смещения, А > 0,/z > О — постоянные Ламе и где для краткости положено ди Эи

Эх ' Эу

Общее (регулярное) решение основных уравнений (13) может быть выражено через две произвольные голоморфные в S функции <р(г),'0(г), следующим образом

Хх + Уу = 4Re р'фф, Уу — Хх + ^iXy = 2 \zp" фф + ф'фф\,

2/z(u + w) = xip^ - гф'фф - ффф,(16)

где                                                 ,_

A + 2/z           ............

x = —----- = 3 — 4ст > 1,

A + /z

• □ ⁼ ДА+Щ ^— коэффициент Пуассона (О < ст < |). Функции рфгф ффф определяются по граничным условиям

<Д£) + 1рфф + ^(1) = /(1) + с(1) при t G L', — хуфф + 1ффф + фф) = /(1)     при t G L".

Здесь L' часть контура L, где заданы внешние напряжения, а на остальной части L" — смещения.

Следуя Д. Н. Шерману [4] функции рфф и ффф мы будем искать в виде

• 1    Г гоф^ p(z) = -- —-dt,

• — х f го^ф 1 f го^ф      1 f Кгфф

фК^ = -- —-dt 4---- -dt------

2тп j t — z     2л% J t — z     2л% J ф — zp

L               L               L где гиф) — функция точки t границы, определяется после решения соответствующего сингулярного интегрального уравнения, полученного из условия (17), с учетом представления (18).

Пусть известна функция гиф), мы дальше ее будем обозначать через рфф

Тогда из (15) получаем

Х_х = 2Re р (г) — Re \zp" ^ + ф' ффф

Y_y = 2Re р фф + Re \фр"^ + ф' фф.

Ху = Тшфр'фг) + ф'фф.

Подставляя значения функции р (г) и ф^ из (18), имеем

Х_х = 2Re — ;^V ’ dt - Re — / ^ dt L                    L L

~^ /~ Ф№      1 f рф№

1 рМФ ^ Ziri J ф — гф ’

2тп J ф-гф 2тп J ф - гф L                  L

У1 = гКе1_!рйХа( + Ке ^[PWL^

^J 2™ J ф- гф        2тп J Ф - гф

L                   L L

-^ f ^ 7/ । ¹ f ^^^

Ziri J ф-гф Z-кг J ф-гф L                 L

1 ptpф^dt

^ J ф- гф L

Xy = Im

^ J ф- гф L

,   — x Г рф^

dt T---- I 7------гл^- dt

Z-кг J ф- гф L

1 f pф)dt 1 ptpф^dt ⁺ 2ivi J ф- гф Ziri J ф- гф

L               L

Аналогично для компонентов смещения имеем

1 и Г рф^      z Г рф^

и = —Re   / ----- dt -\--/  ----- -ту dt

Zp    |_2тгг J t — z      Z-кг J ф — гф

LL гт«1 e-2 2rJ t-z 2m J (i-z)2P L                LL

1 т Г x Г рфА z Г рфА v = 7Г~Im ^—7   ---- dt + -—;   -

Zp [2тгг J t — z Ztx% J ф — гф LL x f рф) 1 7 рф) 1 f МФ ] Z-кг J t-z ZiriJ t-z Z-кг J ф-гф\

L                LL

Значения полученных интегралов типа Коши можно вычислять с помощью квадратурных формул, построенные в §1.

Таким образом, легко можно вычислять компоненты напряжения.

ЗАМЕЧАНИЕ. В выше указанных вычислениях возникают определенные трудности. В частности, при вычислений разделенных разностей, когда. ф,фф^ совпадают, разде-

ленные разности переходят в производные. Для них справедлива

У^о,Д) = <АМ

^(Д,Д,Д) =

^о) 2!

?(t, W!,t2)

АМ

2!(t0 - t)

Е!У_^ХМ1 0«-1У ⁺ «0-1)2

при Д = Д;

при Д = Д = Д;

при t ^ t₂ = Д = Д.

Полученные выражения лучше вычислять с помощью следующих (см. [3]) формул:

2 v'uo = Е /.• = -2 /.•^0

П (Ф - К А

3=~2

2^0

П А+к

3 = ~2

3*0,к

TV*3 )

(Д   Tv А

. Ам

5!

JJ (Д — Tv-VjV з=-1

з*о

_V"(к = _-з к^О

П (д-^+д j = -22

„ К л .С^^,

(Д Ту^^ ф[ VTv*k Tv*^

3=-2 3*0,к

П (Д ” К+Ч

3 = -2

3*0

П 4"v*-k ^{— Т}13*3^

3 = -2

3*0,к

,,«,) - V(7,+t) «о - г„+1)=

АЧ^ ^^ 6!

JJ (Д — ^Tv*3^

з = -1

з*о

to G ТуТу-\-3.