О причинности в квантовой теории

Понятие причинности имеет несколько значений. Квантовая наблюдаемая, не находящаяся в собственном состоянии измеряемой величины, в серии экспериментов принимает различные значения, подчиняющиеся вероятностной статистике. Что предопределяет конкретное значение измеренной величины в единичной реализации? Эйнштейн, Подольский и Розен [1] считали, что некая совокупность скрытых параметров, которыми следует дополнить квантовую теорию. Бор же настаивал на принципиальной непредсказуемости результата (см., напр., [2] ) и полноте квантовой теории без всяких скрытых параметров. Эта точка зрения и получила свое экспериментальной подтверждение в серии работ, начиная с Белла [3 –10] . В этом смысле можно говорить о « беспричинности » результата квантовых измерений, поскольку принципиально невозможно его заранее предсказать [2] .

Другое значение понятия причинности связано со световым конусом и СТО: следствие не может наступить раньше, чем причина, причем скорость причинно-следственной связи между ними не должна превышать световую. Однако целый ряд экспериментов с так называемым отложенным выбором и квантовым ластиком опровергли и это понятие причинности: скорость причинно-следственной связи в них на несколько порядков превышала световую (см., напр., [11, 12] и цитируемую там литературу). Но следствие при этом не опережало причины. Следующий по значимости эффект с точки зрения причинности связан с квантовым парадоксом Зенона (см., напр., [13, 14] и цитируемую там литературу). В нем два последовательных квантовых перехода как бы нарушают причинность в самом широком смысле этого слова: второй по времени переход определяет вероятность первого. В самом деле, единичная вероятность второго перехода обращает в ноль вероятность первого, то есть полностью блокирует его. Но с другой стороны, нулевая вероятность первого также блокирует второй, поэтому скорее следует говорить об их равноправности, поскольку вероятность обоих переходов является результатом интерференции амплитуд вероятностей обоих переходов, то есть квадратом модуля суммы их комплексных амплитуд.

Рассмотренный далее эффект переворачивает причину и следствие во времени, что ведет к нарушению причинности в самом широком смысле этого слова. Он связан с квантовым парадоксом нелинейного светоделителя [15 –20] , в котором фазовые флуктуации света возникают как бы из ничего [21] . Позже появилась работа, развивающая прикладную направленность этого явления [22] . Однако дальнейшее исследование парадокса приводит к еще более интересным последствиям, которые уже касаются фундаментальных основ квантовой теории, и ее интерпретаций.

Чтобы легко войти в смысл задачи, рассмотрим нелинейный светоделитель, представляющий собой границу раздела двух прозрачных диэлектриков ( Рис. 1 ). Пусть один из них обладает кубической керровской самофокусирующей нелинейностью, обуславливающей увеличение показателя преломления с ростом интенсивности излучения. Коэффициенты пропускания и отражения такой границы раздела изменяются с изменением интенсивности света в соответствии с формулами Френеля. Пусть линейная среда предшествует нелинейной, и показатель преломления второго диэлектрика в рабочем режиме, то есть с учетом нелинейной добавки, превышает показатель преломления первого: тогда с увеличением интенсивности излучения увеличивается и показатель преломления, следовательно, увеличивается коэффициент отражения границы раздела, а коэффициент пропускания снижается. Следовательно, флуктуационное увеличение интенсивности входного пучка будет частично компенсироваться уменьшением коэффициента пропускания. Таким образом, происходит насыщение или некоторое « запирани » системы, приводящее к стабилизации интенсивности прошедшего света. Ощутимая стабилизация может проявляться и в отраженном от границы раздела пучке, если показатель преломления с увеличением интенсивности излучения, напротив, уменьшается, либо изменено соотношение показателей преломления: первый больше второго.

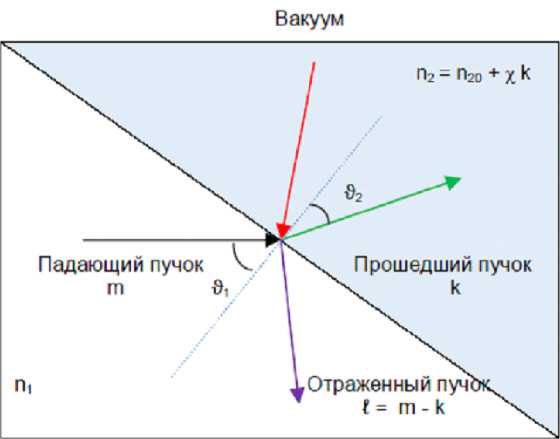
Рис. 1. Нелинейный светоделитель со второй нелинейной средой. $ 1 и // 2 — углы падения и преломления. На первом входе когерентная мода с плоским волновым фронтом, а на втором — вакуум.

Рассмотрим одномодовый случай плоских монохроматических волн. Фаза плоской волны вблизи плоской границы раздела прозрачных сред, отраженной либо прошедшей, инвариантна с точностью до возможного скачка на т — в отраженном пучке. При этом складывается парадоксальная ситуация: амплитудные флуктуации прошедшего либо отраженного пучка могут уменьшаться, а фазовые должны оставаться неизменными, что, конечно, приведет к нарушению принципа неопределенности Гейзенберга. Исследованию возникающей при этом коллизии в основном и посвящены работы [19–21]. Здесь же мы исследуем результаты точного квантового расчета с точки зрения их интерпретации. Дело в том, что итоговый результат — число зарегистрированных фотонов на выходах светоделителя — зависит от значения нелинейной добавки к показателю преломления. Но до момента регистрации число фотонов не определено (см., напр., [14] и цитируемую там литературу). Таким образом, получается, что конкретное значение нелинейности появляется только после регистрации фотонов на выходах. Но детектирование происходит после прохождения светом светоделителя. Следовательно, нарушается принцип причинности в самом общем его виде, когда последующее событие определяет предыдущее. Такова краткая логика рассуждений, более подробно рассмотренная далее.

Для того чтобы не учитывать фазового набега в прозрачных средах, мы рассматриваем пучки именно вблизи (на расстоянии не более длины волны) границы раздела. Кроме того, выделение такого узкого слоя (например, в результате размещения его между двумя плоскопараллельными пластинами из линейных материалов) избавляет нас от эффекта неустойчивости плоской волны в среде с самофокусировоч-ной нелинейностью, являющегося классическим результатом нелинейной оптики, поскольку на малой длине распространения света неустойчивости не возникает.

2.    Классическое описание светоделителя

Рассмотрение преломления света границей раздела двух сред естественно начать с закона Снелли-уса:

« 1 sin 19 1 = « 2 sin 1 2                                             (1)

и формулы Френеля для амплитудного коэффициента отражения [23] :

sin (1 1 - I 2 )

sin (11 + 12) ’ которая справедлива в случае плоско-поляризованного света с вектором напряженности электрического поля, перпендикулярным плоскости чертежа (так называемая s-поляризация). Для другой, взаимно ортогональной поляризации (р-поляризации), синусы заменяются тангенсами.

Если нет потерь, то коэффициенты пропускания и отражения связаны простым соотношением т2 + р2 = 1,

следующим из закона сохранения энергии.

Сразу отметим, что анализируется только случаи режимов прохождения света, а, полное внутреннее отражение из рассмотрения исключается.

Нелинейность одной из граничащих сред означает зависимость ее свойств от интенсивности пронизывающего ее излучения. Например, керровская нелинейность влияет на показатель преломления. В случае первой нелинейной среды:

« 1 = « 10 + X (V™ ± Vl^ ,     « 2 = const,

(2.4a)

поскольку в первой среде одновременно присутствуют и падающая, и отраженная волны. Они складываются когерентно, в отклике среды возникают интерференционные нелинейные члены и, в общем случае, волны становятся кноидальными, однако последние возникают в объеме среды, а мы рассматриваем тонкий слой вблизи границы раздела, где фазовый набег отраженной волны либо отсутствует, либо равен т — при отражении от более плотной среды. В последнем случае в формуле ( 2.4a ) следует брать разность амплитуд (V™ — V l), а при отражении от менее плотной среды — сумму (V™ + Vl^ .

Для второй нелинейной среды — проще:

« 2 = « 20 + х^,    « 1 = const,

(2.4b)

где n^ — показатель преломления в темноте, а % — коэффициент, пропорциональный кубической нелинейности среды % ⁽³⁾ . Для удобства сопоставления с квантовым подходом, интенсивность света мы условно измеряем числами фотонов в некотором объеме квантования. Эти безразмерные величины, разумеется, пропорциональны интенсивностям рассматриваемых плоских монохроматических волн.

Совместное решение системы уравнений ( 1 ) – ( 4 ) с учетом очевидных соотношений для комплексных амплитуд прошедшей и отраженной волн:

d = та _г ,

а _т = [ХЦ

даст искомое соотношение между входной и выходными волнами. Индексы t, г, г относятся к проходящему, отраженному и падающему пучкам. Аналитического решения, к сожалению, получить не удается. Поэтому для исследования статистических характеристик такого пассивного нелинейного преобразователя приходится прибегать к численному эксперименту [21] . Но, как это ни странно, квантовое описание все же допускает возможность аналитического решения.

3.    Точное квантовое решение в представлении Шрёдингера

Пусть светоделитель ( Рис. 1) освещается слева модой в фоковском состоянии | т > с определенным числом фотонов т . Но потенциально у него есть и другой вход — сверху Даже при отсутствии на нем излучения, там будет вакуум | 0 > . Если бы светоделитель был линейным, то состояние на выходе описывалось бы вектором [24] :

m w> = Е Vcm тк     |k} ii},                                (6)

к =0

здесь прошло k фотонов, а отразилось i = т — k, т и р — френелевские амплитудные коэффициенты пропускания и отражения, С™ — биномиальный коэффициент.

Это соотношение является точным квантовым результатом, однако, оно имеет простой физический смысл: фотоны в данном случае ведут себя как обычные классические несвязанные частицы. Например, вероятность прохождения одного фотона равна т 2 , а k фотонов — т ^2к . Вероятность того, что прошло k фотонов, а отразилось i = т — k равна произведению (г²) • (р²) ^т . Биномиальный коэффициент С’т = _к |(, т -_к )! появляется вследствие эквивалентности всех возможных сочетаний прошедших и отраженных фотонов. А поскольку вектор состояния представляет собой не саму вероятность, а ее амплитуду, извлекаем квадратный корень.

Нелинейность можно учесть функциональной зависимостью т и р от т ± i в случае первой нелинейной среды, а второй — линейной, и от k — в случае обратного их расположения. В случае же двух граничащих между собой нелинейных сред, обе зависимости будут присутствовать одновременно. При этом можно использовать обычные формулы для т и р ( 2 ) и ( 3 ) с учетом того, что нелинейная добавка показателя преломления пропорциональна числу фотонов в среде, а коэффициент пропорциональности %, в свою очередь, пропорционален коэффициенту кубической нелинейности % ⁽³⁾ .

При произвольном состоянии на входе |> , например, когерентном | z > , его можно разложить по фо-ковскому базису:

∞

|> = Е Dm |т>,(7)

m=Q тогда тт

№« Е Dm Е^т к( k И k )|k}|т — k Е Dm Е Лк1 |k>|i> .(8)

m=Q    к=0         '     '   '     '               m=0

Здесь двухэтажные аргументы при т и р означают зависимость от верхнего или нижнего этажа для той или иной последовательности расположения нелинейной и линейной сред, о чем было сказано выше. В силу нелинейности задачи приходится производить перенормировку, чтобы выполнялось (' ^ |' ^ } = 1.

Физический смысл квадратов коэффициентов Л ^ = |( Z 1(кЦ ^ }| ² очень прост: это вероятность того, что пройдет к фотонов и одновременно отразится Z, то есть мы имеем дело с двумерной условной вероятностью. Теперь нетрудно найти распределения вероятностей обнаружить определенное число фотонов в отраженном и проходящем пучках:

∞∞

Р = £ Л к„    р _к = £ л^.                        (9)

к =0                1 =0

В этом переходе от линейной задачи к нелинейной есть одна очень важная тонкость. Если на входе было фоковское состояние, то на выходах, разумеется, нет: число фотонов к и Z может быть разным. Точнее, выходные состояния представляют собой суперпозицию фоковских. Так какому же из них должна соответствовать нелинейность? Будем рассуждать операционально. Если мы детектируем на выходах фотоны, то в каждой реализации мы получим вполне определенное их число к и Z. Именно этим числом и будет определяться нелинейность, что и отражено в ( 8 ). И на входе их было, таким образом, тоже определенное число т = к + Z.

Хотя формально здесь все верно, возникает вопрос: откуда нелинейность светоделителя заранее « знает » сколько фотонов будет зарегистрировано на выходах? Ведь если поле внутри светоделителя находится в состоянии суперпозиции фоковских состояний, то, значит, в нем присутствуют все фоковские моды (см., напр., [14, 25] ). Так какие из них должна « выбрать » нелинейность, чтобы сошлись концы с концами? Без опережающего знания о последующем детектировании выходных полей это просто невозможно. Значит, нарушается принцип причинности в том смысле, что последующее событие определяет предыдущее, что вполне укладывается в рамки реляционно-статистической природы закономерностей квантовой теории (см., напр., [26] и цитируемую в ней литературу).

4.    Заключение

В данной работе представлена квантовая теория преобразования бозонных полей нелинейным светоделителем, представляющим собой плоскую границу раздела двух прозрачных сред, одна из которых или обе обладают кубической керровской нелинейностью, то есть показатель преломления зависит от интенсивности пронизывающего излучения. Характерным свойством квантовых состояний, не являющихся собственными состояниями измеряемой величины, оказывается наличие квантовой суперпозиции всех возможных результатов измерений. Если рассуждать операционально, то для описания такой нелинейно-оптической квантовой задачи нужно начинать с конца — с количества фотонов, зарегистрированных на выходах светоделителя. Затем, « раскручивая » процесс в обратном (по отношению к реально текущему времени) направлению, определяем число фотонов в нелинейно-оптической среде светоделителя и соответствующую нелинейность. После чего задача получает строгое аналитическое решение. Но, как часто бывает в квантовых задачах, возникает вполне закономерный с точки зрения « здравого смысла » вопрос: что происходит между рождением квантовой частицы и ее регистрацией? Что первично: нелинейность, формирующая выходные поля светоделителя, или количество фотоосчетов, которые определяют нелинейность? Если следовать хронологическому порядку, то ясно, что первое. Но до момента регистрации (априори) определенного числа фотонов в нелинейной среде не существует, а есть лишь квантовая суперпозиция фоковских состояний. Значит, и определенной нелинейности не существует до момента финальной регистрации частиц. Итак, последующее по времени событие определяет предыдущее. А это несомненно нарушает принцип причинности в самой общей его формулировке.