О приложении теории оболочек к некоторым задачам офтальмологии

В настоящее время широко распространенными рефракционными операциями по поводу миопии и миопического астигматизма являются операции лазерного кератомилеза in situ и фоторефрактивной кератэктомии [1]. В результате этих операций меняются толщина и кривизна роговицы. В связи с этим представляет интерес вопрос об изменении напряженно-деформированного состояния роговицы после указанных операций. В работе [2] этот вопрос исследовался в предположении, что склера является значительно более жесткой, чем роговица, и, таким образом, роговица рассматривалась как жестко защемленная пологая оболочка. Однако в литературе имеются разные данные о соотношении модулей упругости склеры и роговицы. Например, в работе [3] полагается, что Ei / E2 = 5, а в работе [4] выявлено, что Ei / E2 = 3.

С точки зрения механики задача о последствиях операций рефракционной хирургии и изменении прочности роговицы при различных соотношениях E _i / E ₂ моделируется как задача о напряженно-деформированном состоянии двух сферических изотропных оболочек, сопряженных по окружности, находящихся под действием равномерно распределенного внутреннего давления.

Склера представляется незамкнутой однородной сферической оболочкой. Напряженно-деформированное состояние оболочки найдено на основе решения, полученного методом асимптотического интегрирования комплексных уравнений В.В. Новожилова [5]:

- B sin P _i ) e ^{P i} +

R i ² q (i -Ц 1 ) 2 E _i h

w (1) = _^_( a _C os в

E i h i

₊ qR i

2 ’

N "' =— ^ctg 0 (( A - B )cos P i - ( A + B )sin e i ) e -^Pi

V² R i

N ₂ ⁽ⁱ⁾ = ( A cos P _i - B sin P _i ) e ^P + qR^

M ₂ ⁽ⁱ⁾ = g M _i ⁽ⁱ⁾; M _i ⁽ⁱ⁾ = - c _i ( B cos P _i + A sin P _i ) e ^{-P i},

(( A - B ) cos P _i - ( A + B ) sin P _i ) e ^P ,

9 ^(i, = TT J^AA + B )cos P i + ( A - B )sin P i ) e

-

^{P i}; u ⁽ⁱ⁾ = C sin 0 ,

(i)

E_i h 2 c _i

P i = 4 3(i -g i ²), R -( O-O o ),

Ci Vi2(i-gi2) ’ где w(1) - прогиб оболочки, Ni(i), N2(i) - усилия, Mi(i), M2(i) - моменты, возникающие в оболочке, Q(i, 9(i), u(i) - перерезывающая сила, угол поворота и перемещение оболочки, соответственно. Верхний индекс указывает на принадлежность к склере. 0 -угол, образуемый нормалью к срединной поверхности с осью оболочки, 00 - угол, определяющий край оболочки; hi, Ei, Ri, g - толщина, модуль упругости, радиус, коэффициент Пуассона склеры, соответственно; q - внутриглазное давление; А, В, С -константы интегрирования.

Сопряженная со склерой роговица рассматривается как пологая однородная изотропная оболочка другого радиуса. Напряженно-деформированное состояние роговицы найдено с помощью решения комплексных уравнений пологих оболочек, полученных А.А. Назаровым [6]:

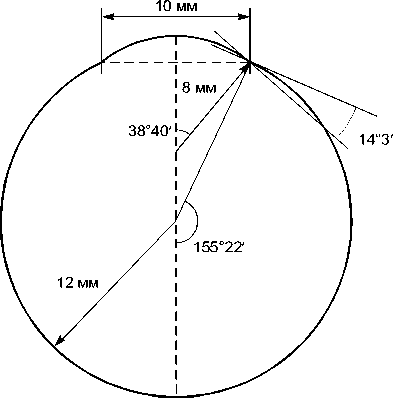
Рис. 1. Схематическое сопряжение роговицы и склеры

w(2) = C1 + A1I1 + B1I2, n«1 = qL+HEA (B1■+Ai2), 4 f а

N ⁽²⁾ = q- — N ⁽²⁾ — 2 fE.h ( AL + BI ),

2      2       1           2 2   1112

M 1^{( 2} ' = £( A ( 1 2 + ^ I ,' ) — B ( 1 1

—

^ 1 2 )), а

к2

M 2 ⁽²⁾ = D ⁽¹ + ^ ) ( A1 2 — B 2 1 1 ) — M ^

Q<2> = D(AI‘ — BI‘), э(2) =—1 — + —, 1 к312   11         к dа u (2) = ( 1 ц 2 )k qa

к2

4 f E 2 h 2 h ₂

4 f 73(1 — ц ²)

+ 2 fk (1 + Ц 2 )(, ¹ а + AI 2 — BI 1 ), 1 + ц

,   1           E₂h³         ,

-, J = —, D =          , r = к а ,

2 R      12(1 — ц ²)

где 1 ₁ , 1 ₂ , 1 1 , 1 2 - значения действительной, мнимой составляющей функций Бесселя нулевого порядка и их производные, соответственно, h ₂ , E ₂ , R 2 , ц ₂ - толщина, модуль упругости, радиус, коэффициент Пуассона роговицы, соответственно, r - полярная координата, D - жесткость на изгиб, q - равномерно распределенное внутриглазное давление.

На линии сопряжения оболочек выполняется шесть условий непрерывности перемещений, момента, усилий и угла поворота [7]:

u ⁽¹⁾ = u ⁽²⁾ cos у — w ⁽²⁾ sin у , w ⁽¹⁾ = w⁽²⁾ cos y + u ⁽²⁾ sin y , M 1 ¹ = M 1 ⁽²⁾,

N ⁽¹⁾ = N^ cos y — Q^ sin y , Q^¹ = Q 1 ⁽²⁾ cos y + N ⁽²⁾ sin y , 3 ⁽¹⁾ =3 ⁽²⁾,

где γ – угол между касательными к оболочкам 1 и 2 (рис. 1).

Таким образом, аналитическое решение задачи о напряженно-деформированном состоянии сопряженных сферических оболочек может быть найдено c помощью систем (1), (2) и (3). Постоянная С в системе (1) фиксирует начало отсчета осевого смещения. В нашем случае С = 0.

В среднем радиус склеры – 12 мм, роговицы – 8 мм, толщина склеры – 0,5 мм, коэффициент Пуассона – 0,4 для склеры и 0,45 для роговицы, модуль Юнга склеры – 14,3 МПа [8]. Расчеты проводились для различных значений внутриглазного давления. Известно, что после операций фотореактивной кератэктомии уменьшается кривизна роговицы при увеличении ее толщины. Операция лазерного кератомилеза in situ основана на уменьшении толщины роговицы.

Основные растягивающие напряжения роговицы при воздействии на нее qR внутриглазного давления (q) равны σ =  2 . Изгибающее усилие рассчитывается при p 2h2

6M максимальном моменте, возникающем в оболочке: σ = max . По сумме напряжений из       h22

σ

σиз и σ можно оценить запас прочности роговицы η =    *   . Разрушающие p                                          σ +σ из p

Н напряжения для роговицы лежат в диапазоне σ _* = 5,38 ÷ 9,79 ⋅ 10⁶ ₂ .

м2

В таблице 1 приведены характеристики, полученные для роговицы при повышенном внутриглазном давлении 40 мм рт.ст., до и после операции лазерного кератомилеза in situ . Видно, что при уменьшении толщины роговицы на 0,1 мм после операции лазерного кератомилеза in situ коэффициент запаса прочности в среднем понижается на 13,95 %.

Отметим, что при моделировании последствий операции фотореактивной кератэктомии радиус кривизны роговицы уменьшался на 1 мм, а толщина увеличивалась на 0,1 мм, в результате при расчете задачи для разных значений модуля упругости роговицы максимальный абсолютный прогиб в центре оболочки понижается в среднем на 39 %. Все расчеты проводились в программе Mathematica 5.1.

Таблица 1

Характеристики роговицы до и после операции лазерного кератомилеза in situ при внутриглазном давлении 40 мм рт. ст.

Толщина роговицы	h = 0,52 мм			h = 0,42 мм			η 1 / η 2
	w m(2a)x,10 - 6м	H σ u3 , м2	η 1	w m(2a)x,10 - 6м	H σ u3 , м2	η 2
E = E 1 2    10	93,36	16930	134,49	113,38	18408	114,53	1,173
E 1 E 2 = 5	46,42	15560	139,23	56,36	16602	119,11	1,168
E = E 1 2 3	27,80	15208	140,54	33,47	14960	123,59	1,137

Роговица

Сосудистая оболочка

Хрусталик

Склера

Сетчатка

Стекловидное тело

Решетчатая пластинка

Глазной нерв

Рис. 2. Строение глаза

Аналогичная математическая постановка позволяет описать деформацию решетчатой пластинки глаза при глаукоме.

Известно, что атрофия зрительного нерва при глаукоме происходит именно в области решетчатой пластинки глаза в результате ее деформации, если отношение внутриглазного и внутричерепного давлений увеличивается по сравнению с нормальным для конкретного пациента значением.

Решетчатая пластинка представляет собой часть склеры недалеко от заднего полюса, где оболочка становится существенно тоньше и имеет множество мелких отверстий, через которые проходит зрительный нерв (рис. 2). Таким образом, модуль упругости решетчатой пластинки значительно меньше модуля упругости для склеры и можно положить E 1 / E 2 = 10.

Было бы легче рассмотреть решетчатую пластинку отдельно, чтобы учесть ее анизотропию и неоднородность, как рассмотрено в задаче [8]. Однако решетчатая пластинка является частью склеры, поэтому интересно учесть влияние на поведение пластинки растягивающей силы, действующей со стороны склеральной оболочки глаза. Решетчатая пластинка предполагается однородной и изотропной.

В настоящей работе проводится сравнение аналитических решений задачи о деформации составной оболочки (склеры и решетчатой пластинки) и отдельно задачи о деформации решетчатой пластинки под действием нормального давления. Изучается влияние увеличения внутриглазного давления на диаметр склерального кольца, а также влияние деформации сферической оболочки глаза на величину прогиба решетчатой пластинки. В задаче о спряженных оболочках решетчатая пластинка считается пологой оболочкой того же радиуса, что и склера. Ранее подобная задача рассматривалась в прикладном пакете Adina , поэтому представляет интерес сравнение аналитических и численных результатов [9].

В таблице 2 представлены значения прогибов решетчатой пластинки как пологой оболочки ( w 1 ) с жесткой заделкой, когда u | r = a = 0, w | r = a = 0, w | r = a = 0, пластины ( w 2 ) с жесткой заделкой, а также в сопряжении со склерой ( w 3 ). Для последнего случая найдены изменения радиуса склерального кольца для различных величин внутриглазного давления, r = A x = w₃ • sin 0 0 .

Толщина решетчатой пластинки принималась в расчетах 0,25 мм, модуль Юнга 1,43 МПа, основание пластинки 2 мм, радиусы кривизны оболочек 12 мм, коэффициент Пуассона 0,45, толщина склеры 1 мм.

Таблица 2

Характеристики решетчатой пластинки при повышенном внутриглазном давлении в разных постановках задачи

q , мм рт.ст.	15	30	40	50	60	80
w 1 , мм 10 - 3	13,05	26,1	34,8	43,05	52,21	69,61
w 2 ,мм 10 - 3	13,38	26,76	35,68	44,6	53,53	71,36
w 3 , мм 10 - 3	13,65	27,3	36,4	45,51	54,61	72,8
Δ r , мм 10 - 3	1,13	2,27	3,03	3,79	4.55	6,06

Сравнение результатов, полученных для составных оболочек и упрощенной модели, показывает, что разница в значениях максимальных прогибов 4,39-5,40 %, а изменение радиуса склерального кольца существенно меньше прогибов и им можно пренебречь. Таким образом, деформацию решетчатой пластинки, по-видимому, можно изучать отдельно от деформации склеральной оболочки.

Благодарности

Работа выполнена при поддержке РФФИ, грант № 04-01-00258.