О применении барицентрического метода в численном решении внутренней задачи электродинамики

Барицентрический метод (БМ) относится к вариационным методам (методы конечных разностей, конечных элементов, импедансного аналога электромагнитного пространства [1]), применяемых для прямого численного решения уравнений электродинамики вида:

V²Ф + к²Ф = 0; V² A + к² A = 0;

„ 2 ^-        а² A      -

V A - еаца 5" = -цаJ , dt2

где Ф и А являются либо электродинамическими скалярным и векторным потенциалами, либо определяют продольную составляющую вектора и непосредственно вектор напряженности электрического E или магнитного Й поля; к — волновое число; б a и ц a — диэлектрическая и магнитная проницаемости среды соответственно; J — плотность тока.

Идея БМ [2; 3] и его отличие от известных методов вычислительной электродинамики состоит в обобщении процедуры аппроксимации потенциала при численном решении внутренних задач Дирихле и Неймана без разбиения области анализа Q на элементарные подобласти. Допущения БМ связаны с тем, что: 1) решение формируется в барицентрической системе координат Z1 (P) , Z2 (P) , ..., Zn (P), позволяющей однознач- но определить точку аффинного пространства P ей через точечный базис Pi, P2, ..., Pn — вершины Q; 2) Q — односвязная однородная область с кусочно-линейной границей

N г = U Г n, n=1

где ^Г n = { e n t ⁺ P , t ^е [ 0, 1 ] } ^при e n = P n + 1 ^- P n .

Основной этап БМ состоит в определении барицентрических координат (БК) для Q, которые должны удовлетворять свойствам [4; 5]:

N

• 1)    ^ Z n ( P ) P n = P ;

n = 1

• 2)    Z n > 0 ( n = I? N ) ;

N

• 3)    Z Z n = 1;

n = 1

• 4)    AZ n = 0 при

Z„( P -) = 5 n ' =|^1, n = n’ (n , n е (1? N } ). nn n

[0, n * n ,

Методы определения гармонических БК основаны на: 1) геометрическом подходе [5] – построение проекций Г _n на дуги единичной окружности B ₀, положение которой определяется из решения задачи конформного отображения Q на B ₀ (решение задачи конформного отображе-

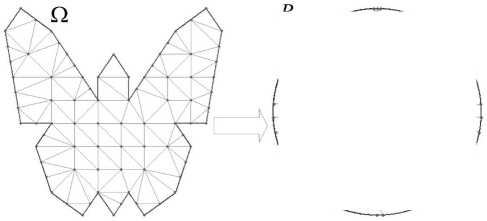
Рис. 1. Пример решения задачи конформного отображения Q на B q

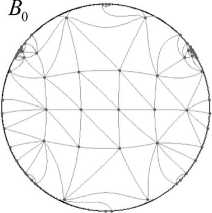
h — 1

Wh, m =П( v — m )( m + 1 + v)( v + 1)—2, v=0

W = 1, R = P — P и выполнении условий 0,m        n,n     n n n * n', n + 1 * n' и n * n' + 1 [8]:

c n , n ‘ m , m '

m + m '+ 1

z Im ^b

I

ния предлагается осуществлять методами [6; 7], пример решения задачи представлен на рис. 1);

2) аналитическом подходе, который рассмотрен в [8] и связан с решением задачи Дирихле:

I ^R n , n

+ I ----

V e n

h = 1 h Г

ln

h

I ^R n , n + 1 I — ------

V e n J

1 n,n'      - ln h—1, m, m

( R .

R n + 1, n

V   ^vn , n  J

ln

V

h

+ z 1

v = 1

(R . , . ^Rn + 1, n + 1

R

R n + 1, n '+ 1 R n + 1, n -   .

v

^— e n

v R.

V

■ n , n ' _v

h

+z v

— e

v R.

^^^^^^в

+

Av D

' n , n ' + 1

;

AZ n ( P ) = 0, P e Q;

Z n ( P ) = t , P e Г n — 1 ;

Z n ( P ) = 1 — t , P еГ n ;

Z n ( P ) = 0, P еГ \ {Г n — 1 , Г n } •

Решение задачи (1) при задании Qc С

в [8]

^

Dⁿ , ^{n -}, = m , m

J 7

определено ношением

приближенно-аналитическим соот-

Г    L ⁽ m ^—1V 2 J

—2 z

v = 0

m + m '+ 1

X z в h=1

2 ( m — 2 v ) — 1 ( 2 v + 1 ) ( m — v )

’h —-1, m — 2 v — 1, m ', ^m >  m ^;

0, m <  m ';

NM

Z M (P ) = X- zz 2m+1Q Qm X 2n n =1 m=0

‘

Bn, h, m, m   h + 1

A (

z v=0 V

x|2 P

—

P n -

—

m + m'

n , n ‘ J

r

v

X

en'

n

¹ I ^X n , m ,

х W h

, — ■

v , m '

обладающим экспоненциальной скоростью димости

схо-

IZ n ( P ) — ^Z M ( P )[

const M 2 ^M

<------------------ 1             •

I c   ( 2 M + 1 ) V 2 M + 3

В выражениях (2), (3) ||»| C определяет норму в пространстве функция из С ( [0,1] ) ; const поло-

Для случаев наличия особенностей в (4) вспомогательные переменные C m ’ nm вычисляются с использованием следующих выражений при выполнении соответствующих условий:

1) n * n -, n + 1 * n - и n = n ' + 1 [8]:

жительна и не зависит от M ; Q_m ( x ) —

многочлен

Лежандра второго рода [9]; XXⁿ = ( E + T )

¹ Uⁿ

–

блочный вектор размера N = N ( M + 1 ) , составленный из элементов X n - _m ; E — единичная матрица размера N x N ; Uⁿ — блочный вектор размера N , составленный из элементов

cn, n - = m, m ‘ m+m '+1

= z Im b h=1

) n '+1, n' h — 1, m , m'

(

, ln

V

R n + 2, n -+ 1 "

^Rn '+ 2, n' ,

+

n

U n ', m =

1, ( n = n ' v n = n ' — 1 ) л m = 0,

-^3, n = n л m = 1, 1/3, n = n' — 1 л m = 1,

0, в др. случаях;

T — блочная матрица размера N х N, составленная из элементов m+m'

tn, n = l—1----V2mA1 x m, m

,             П x/2m' + lfc n,n', +Dn, n'l m, m^     m, m ,

где при обозначении

h

I ^R n + 1, n I

+ I -----“ I X

V ^— e n '+ 1 J

X

ln

R n + 2, n

R n '+1 n -

h

z v

—

v

v R.

I! — 1 h

JJ

;

2) n * n ‘, n + 1 = n ‘ и n * n ' + 1 [7]:

Cn, n = m, m ‘ m+m '+1     ""

= z Im b h=1       L

h

) n, n+1         I Rn+1, n+2 I , ln -------- + h—1, m, m

V V     e n    J

h

X

v = 1

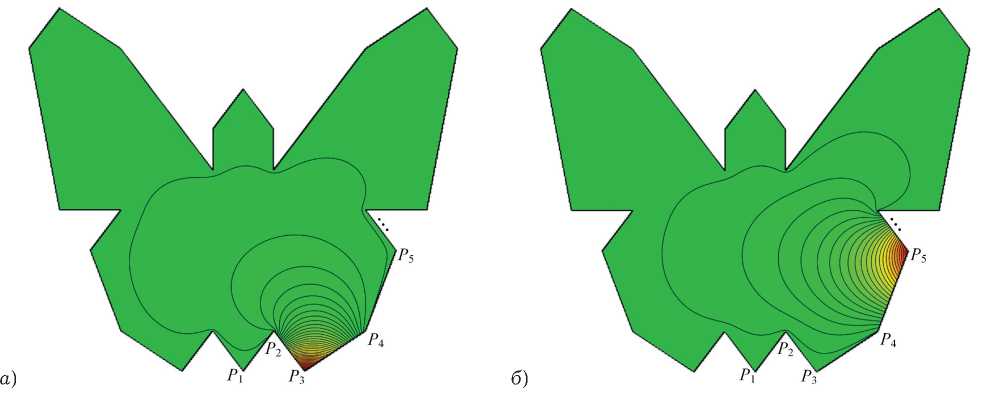
Рис. 2. Пример линий уровня БК Z 3 ( а ) и Z 5 ( б ) для вогнутого многоугольника

ln

R n + 1, n + 2

_ч R n , n + 2 7

+

h

У1

v = 1 v

- e

n

A v 1)

₄ R n , n + 2 ₇

Суть формирования соотношения (2) по заданию гармонических БК по [8] состоит в следующем. Выражение (2) определяет решение задачи Дирихле (1) методом Фредгольма при представлении Z _n в качестве логарифмического потенциала двойного слоя. Формируемое уравнение Фредгольма второго рода относительно неизвестной функции плотности потенциала на Г определяется при численном решении интегрального уравнения методом PG-ядер [10]. Ядро

1 Г            е„,            )

К    (t, s) = Im ---------n--------- n,n п    I ent + Pn - en's - Pn

Точность определения БК зависит от выбора M , при этом высокая сходимость (3) обуславливает высокую точность решения (2) уже при небольших M e [ 5; 8 ] . В подобной постановке БК Z _n определяют функцию формы Q относительно вершины P_n (рис. 2).

Затем в БМ с учетом выбранного правила нахождения гармонических БК задается аппроксимация неизвестного потенциала [2; 3; 11]. На-

пример, аппроксимация

ф( P )= У *!> j a j (P) jeM p скалярного потенциала Ф (P) (P e Q; Фj — коэффициенты аппроксимации) для учета граничных условий на Г (различны при представлении в

интегрального уравнения представляется суммой многочленов Лежандра первого L m ( x ) и второго Q m ( x ) рода:

-2

^К n , n ' ( t , ^s ) = — У ( ^{2 m +} 1 ) L m ( ^{2 s -} 1 ) ^{x П} m = 0

_T In I 9 e n t ⁺ R n , n ' x Im I Q m I 2--------—

e n '

-

при условии

Im I Q m

2 e n t ⁺ R n , n ' .         en'

- 1

= 0

качестве Ф ( P ) продольной составляющей ров электрического и магнитного полей) быть задана через:

• 1)    полиномы Лагранжевого типа [12]: N

«j (P ) = П4 (P);

n = 1

jn a in (P ) = П т (p Z n (P)- k + 1).

k=0 k jn > 0;   a0 (x) = 1;

• 2)    полиномы типа Лежандра:

N a i(P ) = ПаР - in (P);

векто- может

для n = n' . В постановке такого решения соотношения (4)–(6) задают аналитическое представ-

ление интеграла z-Im+m' cn,n- + Dn,n-m, m    m, m

n = 1

«rn ( P ) = Vm ^L0,i m ^{J    (- 1 ) k (} 2 m - ^{2 k} ) !

^mV ’ ^m ^_n k !( n - k )!( n + 1 - 2 k )!

k = 0

x

1                   I

= J L m - ( 2 s - 1 ) Im I Q m

- 1                     ^

2 e n t ⁺ R n , n '

e n '

-

1 I ds .

x[ ( 2Z n ( P ) - 1 ) n + ^1-2 2

m

-

V2 m + 1V2 m + 3 [1, ^m = ⁰;

2 m + 1

V4 m - 2, m > 0;

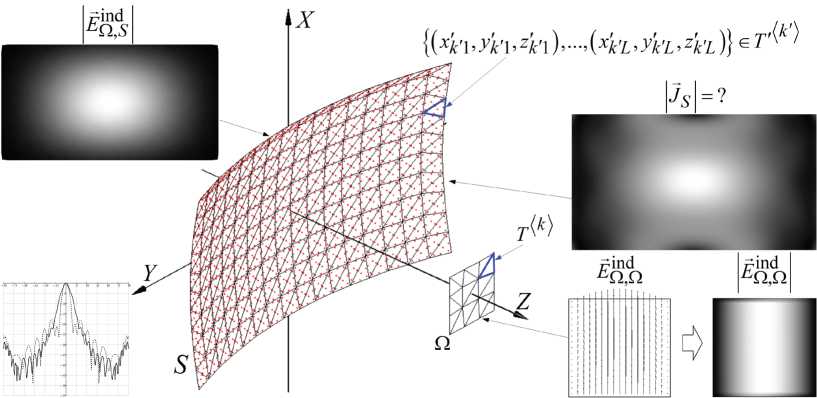
Рис. 3. Пример геометрического представление зеркальной антенны в решении внутренней задачи электродинамики

3) полиномы типа Бернштейна:

N j P )=П"’. (P);

n = 1

“3. ( P ) = j^ « n ( P )) jn- jn !

Здесь p e N — порядок аппроксимации (харак- теризует точность последующего численного решения);

M p = j j = ( j_b j 2 ,..., j . ,-.., j N ) :

jn e ^ jn ^ 0, E jn = P [ n e[1; N ]

– множество мультииндексов j . Аппроксимация

A (P )= E A je j (P) jeMp векторного потенциала A (x) (P e Q; Aj — коэффициенты аппроксимации) задается через БК либо при дифференцировании по соответствующей поперечной координате полиномов (7)–(8)

при задании с их помощью аппроксимации продольной составляющей, либо при обобщении свойств краевых базисных векторных функций

Неделека [2]:

N

в j (P)= Ea jn (P)®n (P), n =1

j n > 0

где

N

j ( p )=a j ( p )nj ( p );

n '= 1

n ^ n '

a j ( P ) — сдвинутый полином Лагранжевого типа [13];

® n ( P ) = [C n ( P ) VZ n + 1 ( P ) -

-Z n + 1 ( P ) VZ n ( P ) ] P n + 1 - P n l

– дифференциальная форма Уитни.

Дальнейшее численное решение волновых уравнений БМ производится аналогично известным вариационным методам и состоит в сведении исходной задачи к системе линейных уравнений (для уравнения Гельмгольца) или обыкновенных дифференциальных уравнений (для волнового уравнения Даламбера).

Также БМ применим для решения сингулярных интегральных уравнений, например формируемых в задачах анализа характеристик зеркальных антенн [14] с учетом постановки модельной задачи дифракции электромагнитной волны на ограниченном тонком экране S [15]:

4n i K E tan = v jj ^ ( v ■ .7 ) dS + JJ к².7^ dS ,     (11)

SS где T = e iKr r^lr - ?'| — функция Грина (r и ?' — радиус-векторы точек наблюдения и источника соответственно); T^tand — тангенциальная составляющая наводимого электрического поля на S.

Для численного решения задачи вида (11) в БМ задается аппроксимация неизвестной функции плотности тока соотношением

. ( P ) = E . j Y j ( ^P ) , j e^M p                                     (12)

Yj (P ) = Й0 ( P )xB j (P ), где тг0 (P) — орт вектора нормали в точке интегрирования P на S.

Затем подстановка аппроксимации (12) в (11) позволяет свести исходное интегральное уравнение к решению системы линейных уравнений по

1,6Х — по Y

Рис. 4. Геометрическое представление анализируемой зеркальной антенны определению Jj — коэффициентов аппроксимации (12).

Пример более подробного решения задачи (11) рассмотрим при описании следующего алгоритма решения внутренней задачи электродинамики зеркальной антенны, включающей один источник электромагнитного поля – облучатель с раскрывом Ω и рефлектор S с раскрывом Ω′ (рис. 3).

Шаг. 1. Разбиение раскрывов Ω и Ω′ на K и K ′ треугольн ых элем ент ов T ^k и T ′ ^k соответственно ( k = 1, K , k ′= 1, K ′) при построении триангуляции Делоне с учетом того, что размер треугольной области ≤λ [16] (λ – длина волны).

Шаг. 2. Выбор в k , k ′-х треугольных областях положений узловых точек интегрирования P_k ′_{′ l} = ( x _k ′ ′ _l , y_k ′ ′ _l , z_k ′ ′ _l ) ∈ T ′ ^k , P_kl = ( x_kl , y_kl , z_kl ) ∈ T^k ( l = = 1, L , где L – число точек интегрирования на отдельном треугольном элементе) при определении для l -х точек соответствующих весов a_l [17].

Шаг. 3. По заданному распределению поля в раскрыве облучателя E — Q'q (поле источника) в точках интегрирования P_k ′_{′ l} определить напряженность электрического поля в ракрыве рефлектора S , наведенного Q, — E kn d = E qS ( Pi ) . Решение выполняется с учетом приближений метода дискретных источников [18] и заданного разбиения области Q при E k n = E n n q ( E k ) :

KL ind              ind 0                   k

E k ′ l ′ = ∑∑ ( E k , l E k , l , k ′ , l ′ Ψ k , l , k ′ , l ′ a l T ) , k = 1 l = 1

где T ^k – удвоенная площадь k -го треугольника области Ω; Ψ _{k , l , k ′, l ′} – функция Грина, вычисленная о тн осительно положения точек P_k ′_{′ l ′} и P_kl при l ′ = 1, L ;

E— 0, l, k', l' = E—k, l, k', l'/Ek, l, k', l' | при Ek, l, k', l' = H0, l, k', l' x nk, l, k', l',

H l 0, l , k', l' = H l k, l , k ', l '/ H k, l , k ', l 'I,

• ¹⁼¹ k , l , k', l' = ri k , l , k', l '/ji^ k , l , k', l '|,

—

Π k , l , k ′ , l ′ = P k ′ ′ l ′ - P kl ,

• ^{—           —} 0          ^— ind

H k , l , k ′ , l ′ = Π k , l , k ′ , l ′ × E k , l ⁰ ,

/I E k n l d|.

^ indg    — ind

E k , l ⁰ = E k , l

Шаг 4 . Определить для заданного положения точек интегрирования P_kl = ( x_kl , y_kl , z_kl ) ∈ T^k , P_k ′_{′ l} = ( x_k ′_{′ l} , y_k ′_{′ l} , z_k ′_{′ l} ) ∈ T ′ ^k на ω и S значения ап-

• —(Q) — s)

проксимационных функций γ _j , γ _j по правилу ^— (Q)     ^—AS j

• (12)    и дивергенций ∇⋅ γ _j , ∇⋅ γ _j . Затем вычислить значения функции Грина Ψ и ее градиента ∇ Ψ относительно положения точек P_k ′_{′ l} , P_k ′_{′ l ′}. При вычислении значений ^ ( r, r' ) и V^ ( r , ^— ‘ ) в пределах одного и того же треугольного элемента при r ^ r' может возникнуть ситуация деления на нуль. чтобы этого избежать по аналогии с [19] в первом приближении предлагается разносить внутренние точки численного интегрирования, определяя их в пределах треугольника для различных ортогональных многочленов (Лежандра, Гегенбауэра, чебышева и пр.) с последующим использованием при численном интегрировании соответствующих квадратурных формул [20].

Шаг 5. Для определенных значений E qQ , E o n' S ,

—Q) — ( S)      — (Q) — S

γj , γj , ∇⋅γj , ∇⋅γj , Ψ, ∇Ψ в соответствую- щих точках интегрирования с использованием Tk , выбранных квадратурных формул [20] и T k , T′ k , al составить соответствующую (11) систему линейных уравнений и вычислить искомый *

— вектор коэффициентов J аппроксимации из (12).

Точность численного решения внутренней задачи электродинамики в БМ определяется размерностью составляемой системы линейных уравнений, которая характеризуется мощностью множества мультииндексов |М _р | при задании порядка аппроксимации p е N . На рис. 5 представлены изменения рассчитываемой J | на поверхности плоского рефлектора (рис. 4) от p при численном решении задачи (11) БМ с представлением числа узловых точек |М _р |.

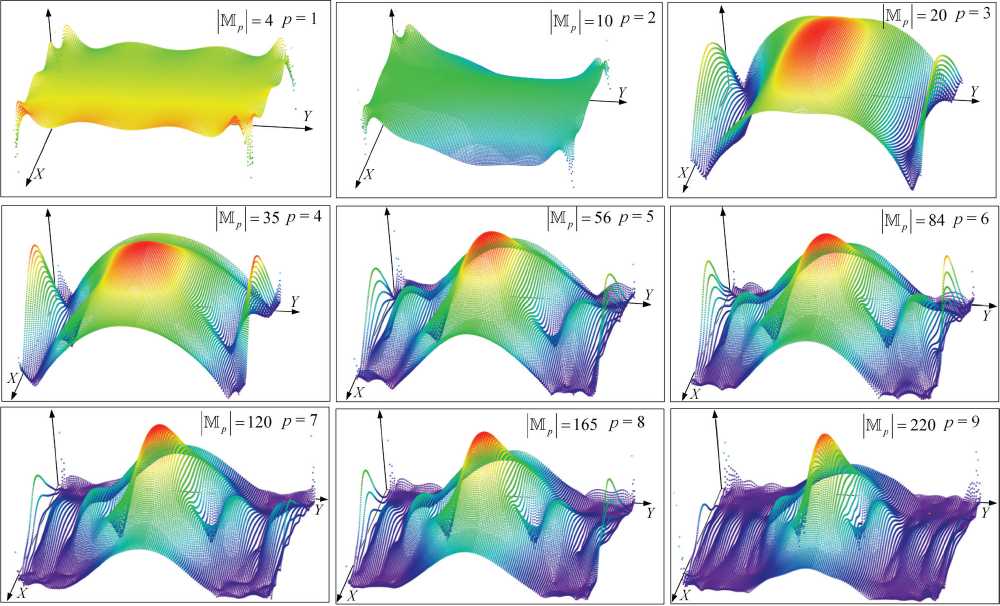
Рис. 5. Изменение расчета , 1 на поверхности плоского рефлектора от p

Основное достоинство БМ связано с тем, что он в сравнении с известными методами при одинаковом порядке аппроксимации позволяет существенным образом (от 2,5 до 5 раз) повысить точность численного решения внутренней задачи электродинамики [2; 3; 11; 12].

Основной недостаток состоит в сложности решения задачи определения гармонических БК для Ω, которая возрастает в случае если Ω является многосвязной областью и сложной относительно геометрической формы структурой.