О применении нейронных сетей в тестировании знаний

Современное обучение немыслимо без систем автоматизированной проверки знаний. Компьютерные системы контроля знаний приобретают все большую популярность, что объясняется не только их объективностью, но и экономической эффективностью.

В последнее время тестовый контроль (ТК) привлекает все большее внимание педагогов в самых разных сферах как наиболее универсальная форма контроля знаний [1]. Проверка знаний в тестовой форме позволяет преподавателю выявить грубые пробелы в знаниях обучаемого и уделить дополнительное внимание общению по теме, недостаточно изученной для допуска к следующей стадии обучения. ТК имеет целый ряд преимуществ [2]: эффективность при самостоятельной работе; объективность в оценке знаний; экономия времени преподавателя; высокая степень дифференциации тестируемых по уровню знаний; возможность индивидуализации процесса обучения; прогнозирование темпа и результата обучения; возможность выявления структуры знаний каждого слушателя для дальнейшего изменения методики обучения. Разработка тестовых заданий (ТЗ) и обработка результатов тестирования подробно изложены в [2] и [3], а известные модели тестирования — в [4].

Задача нейросетевой автоматизации тестирования решалась на Кафедре аэрокосмических измерительно-вычислительных комплексов Санкт-Петербургского государственного университета аэрокосмического приборостроения (ГУАП).

Для проверки принятых решений использовались данные курса подготовки оператора-навигатора (О-Н) летательного аппарата.

НЕЙРОСЕТЕВОЙ ПОДХОД В АВТОМАТИЗАЦИИ КОНТРОЛЯ ЗНАНИЙ

Рассмотрим нейросетевой подход на базе классических ИНС [5] для реализации контрольного тестирования О-Н. Сценарием обучения является тест, состоящий из 7 тестовых заданий (ТЗ), причем каждое ТЗ отличается по уровню сложности. Первое и второе ТЗ теста состоят из 8 подпунктов, третье — из 10 и т. д. (см. табл. 1). Ответом ТЗ является количество активированных обучаемым в текущем ТЗ подпунктов. В соответствии с этим диапазон возможных значений ответа 1-го ТЗ — [0…8], аналогично — 2-го и т. д.

В табл. 1 в строке L пор указано пороговое значение ответа для каждого ТЗ, выше которого ТЗ считается выполненным.

Структура статической ИНС прямого распространения представлена на рис. 1. Нейронная сеть состоит из входного слоя с 7 нейронами, реализующими каждый соответственно по одному из 7 ТЗ теста; скрытого (промежуточного) слоя из 7 нейронов и выходного слоя из 4 нейронов, реализующих оценку в 4-балльной шкале (5, 4, 3, 2) [6]. Все слои связаны друг с другом напрямую и последовательно — без обратных связей и линий задержки [5]. Во входном и скрытом слоях в качестве нелинейной функции одного аргумента

Табл. 1. Сценарий обучения, используемый в задаче автоматизации по нейросетевому методу

Параметр	Тестовые задания							Сумма
Номер ТЗ в тесте	1	2	3	4	5	6	7	баллов
Количество подпунктов в ТЗ	8	8	10	4	7	10	10	57
L max	8	8	10	4	7	10	10	57
L пор	5	5	6	3	4	6	6	35
L min	0	0	0	0	0	0	0	0

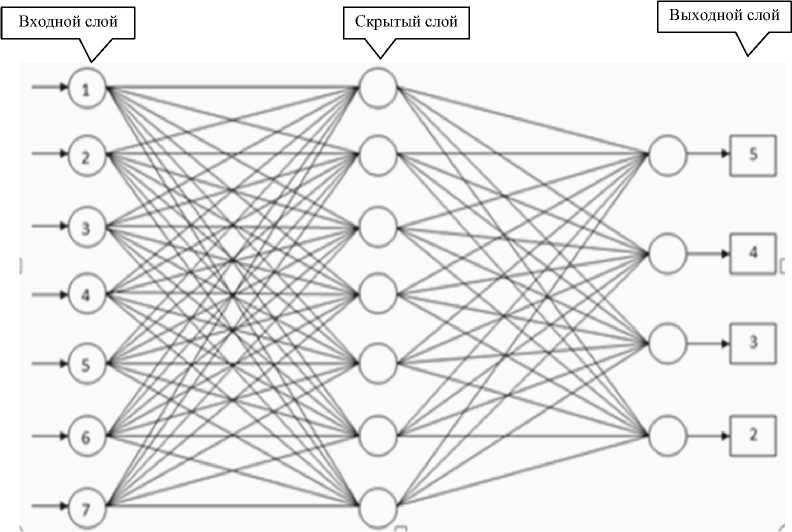
Рис. 1. Структура ИНС прямого распространения для теста из 7 ТЗ и оценки по 4-балльной шкале используется сигмоидальная функция активации (гиперболический тангенс) [7]. Эта функция описывается соотношением [7]

а = tansig( n ) = (ехр( n ) – ехр(– n )) / (ехр( n ) + ехр(– n )).

В выходном слое используется линейная функция активации, эта функция описывается соотношением [7]

а = purelin( n ) = n .

Благодаря свойству дифференцируемости эти функции часто используются в сетях с обучением на основе метода обратного распространения ошибки [5].

На базе программы MATLAB (пакет расширения Neural Network Toolbox) [8] с помощью команды [9]

net = newff([0 8; 0 8; 0 10; 0 4; 0 7; 0 10; 0 10], [7, 7, 4],{'tansig','tansig', 'purelin'})

создается статическая ИНС прямого распространения. Используются вектор входа с 7 элементами, имеющими допустимые границы значений [0…8], [0…8], [0…10], [0…4], [0…7], [0…10], [0…10] — т. е. диапазон возможных значений ответов обучаемого на каждый из 7 вопросов теста (см. табл. 1); вектор выхода с 4 элементами для реализации оценки в 4-балльной системе; функции активации: tansig — во входном и скрытом слое, purelin — в выходном.

После того как сформирована архитектура, производится моделирование и графическое представление сети командой gensim(net) [9].

Табл. 2. Обучающие, контрольные и тестовые статистики (на оценку 5)

№ обучающей статистики на оценку 5 № ТЗ	1	2	3	4	№ контрольной и тестовой статистик на оценку 5 № ТЗ	1	2	3	4
1	8	7	6	6	1	7	7	6	6
2	8	7	6	7	2	8	7	7	6
3	10	9	8	9	3	9	9	6	10
4	4	3	3	4	4	4	3	3	4
5	7	6	5	6	5	7	7	5	6
6	10	9	8	10	6	10	9	8	9
7	10	9	8	7	7	10	8	8	7

На третьем этапе должны быть заданы начальные значения весов и смещений, или, иными словами, сеть должна быть инициализирована с помощью оператора

net = init(net).

После инициализации необходимо произвести процесс обучения, предварительно сформировав некоторую базу обучающих примеров (по 4 образца обучающих, контрольных и тестовых наборов для оценки 5 приведены в табл. 2). Вся информация, которую сеть получает о задаче, содержится в наборе примеров, поэтому качество обучения сети напрямую зависит от количества примеров в обучающей выборке, а также от того, насколько полно эти примеры описывают данную задачу [10]. Считается, что для полноценной тренировки требуется хотя бы несколько десятков (а лучше сотен) примеров [5].

Обучение сети осуществляется с помощью команды [9]

net1= train(net,P,T).

В качестве вектора входа P задают обучающие выборки (табл. 2) из 7 статистик, реализующие оценки 5, 4, 3, 2 с соответствующими значениями целей T (желаемые результаты на выходе). После завершения обучения проводится контрольное моделирование: на вход ИНС подаются контрольные и тестовые выборки (табл. 2), реализующие те же оценки. Если сеть правильно связывает типовое воздействие на входе с эталонными значениями сигнала на выходе, соответствующими требуемой оценке, то принимается решение о том, что ИНС обучена и готова решать поставленную задачу.

Тестирование в автоматизированной системе будет происходить следующим образом. Испытуемому предоставляется возможность ответить на вопросы из предметной области, его ответы предоставляются нейронной сети как вектор входных данных. Сетью производится анализ полученных результатов и выставляется оценка знаний обучаемого в 4-балльной шкале.

НЕЙРОНЕЧЕТКИЙ ПОДХОД В КОНТРОЛЕ ЗНАНИЙ

Нейронечеткий подход в контрольном тестировании знаний испытуемого позволяет использовать совместно аппарат ИНС [5] и нечеткой логики [11]. Сеть в данном случае используется как эффективное средство автоматизации процесса выставления оценок.

В качестве шкалы оценивания взята 12балльная шкала, предложенная в [6]. Достоинством ее по сравнению с традиционной 4-балльной шкалой является более высокая различающая способность. Каждой из возможных "жестких" оценок (2, 3, 4, 5; обычно не используется 1) ставятся в соответствие три оценки из 12-балльной шкалы. Это позволяет описать результат с помощью нечетких понятий "менее чем ..." и "более чем ...", что соответствует оценкам типа "5 с минусом", "3 с плюсом" и т. д., которые часто используются преподавателями. Предлагается соответствие процента правильных ответов обучаемого и оценки по 12- и 4-балльной шкалам (табл. 3).

В описываемой модели использован способ оценки сложности заданий с применением нечеткой математики [12]. Формулируется следующая

Табл. 3. Соотношение процента правильных ответов обучаемого и оценки по 12- и 4-балльной шкалам

Процент правильных ответов	Группа	Оценка	Оценка по 12-балльной шкале	Оценка по 4-балльной шкале
0–10	1	Нет знаний	2–
11–15	2	Неудовлетворительно	2	2
16–20	3	Малоудовлетворительно	2+
21–25	4	Почти удовлетворительно	3–
26–35	5	Удовлетворительно	3	3
36–45	6	Более чем удовлетворительно	3+
46–55	7	Почти хорошо	4–
56–65	8	Хорошо	4	4
66–75	9	Более чем хорошо	4+
76–80	10	Почти отлично	5–
81–89	11	Отлично	5	5
90–100	12	Превосходно	5+

Табл. 4. Нечеткая шкала оценки сложности задания

Параметр Тестовые задания, № 1 2 3 4 5 6 7 Сложность Очень сложное Сложное Выше среднего Выше среднего Среднее Среднее Легкое Баллы 25 20 15 15 10 10 5 Maксим. кол-во баллов 100 Mиним. кол-во баллов 0 нечеткая шкала сложности: легкое, среднее, выше среднего, сложное, очень сложное (табл. 4).

В качестве сценария обучения используются адаптивные ТЗ закрытого типа, состоящие из 7 вопросов, причем каждое ТЗ отличается по уровню сложности (присваивается экспертом): первый вопрос теста оценивается в 25 баллов, второй в 20, третий в 15, и так далее, вплоть до последнего вопроса (см. табл. 4).

Структура статической нейронечеткой сети прямого распространения [7] представлена на рис. 2. Она состоит из входного слоя с 7 нейронами, реализующими каждый из 7 ТЗ теста, промежуточного слоя из 7 нейронов и выходного слоя из 12 нейронов, реализующих оценку в 12-балльной шкале. Во входном и выходном слоях используется сигмоидальная функция активации (гиперболический тангенс). В скрытом слое используется логистическая функция активации, эта функция описывается соотношением [7]

а = logsig( s ).

В программе MATLAB [9] с помощью команды [9]

net = newff([0 25; 0 20; 0 15; 0 15; 0 10; 0 10; 0 5], [7, 7, 12],{'tansig','logsig', 'tansig'})

создается статическая трехслойная ИНС прямого распространения [5]. Используется вектор входа с 7 элементами, имеющими допустимые границы значений [0…25], [0…20], …, [0…5], т. е. диапазон возможных значений ответов обучаемого на каждое из 7 ТЗ теста (см. табл. 3); вектор выхода с 12 элементами для реализации оценки в 12балльной шкале; функции активации tansig — во входном и выходном слоях; logsig — в скрытом.

После того как сформирована архитектура, производится моделирование и графическое представление сети командой gensim(net) [9].

На третьем этапе необходимо провести инициализацию сети с помощью оператора [9]

net = init(net).

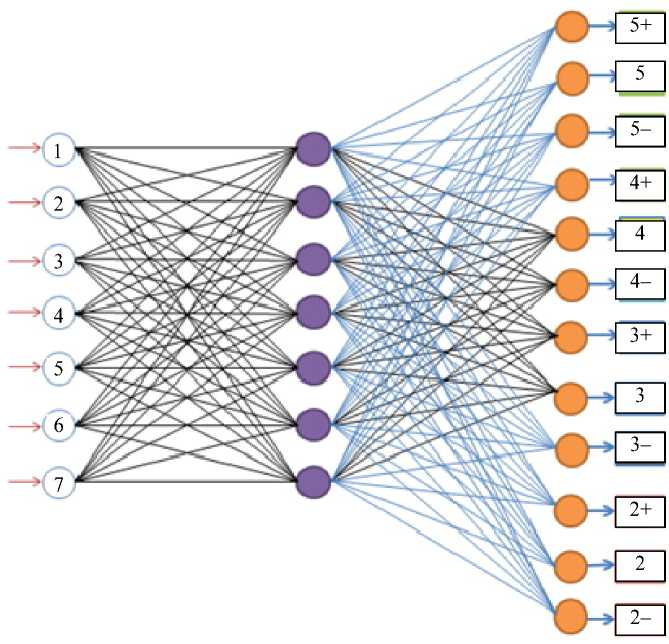
Рис. 2. Структура нейронечеткой сети

Табл. 5. Обучающие, контрольные и тестовые статистики для нейронечеткого контроля навигационных знаний оператора-навигатора (на оценку 4+)

№ обучающей статистики на оценку 4+ № ТЗ	1	2	3	4	№ контрольной и тестовой статистик на оценку 4+ № ТЗ	1	2	3	4
1 2 3 4 5 6 7	0 20 15 15 10 10 5	25 0 15 15 10 10 0	0 20 15 15 10 10 0	25 20 15 0 0 10 0	1 2 3 4 5 6 7	25 20 0 15 10 0 5	25 20 15 0 0 10 5	25 20 0 0 10 10 5	25 20 0 15 0 10 0

После этого производится обучение в соответствии с алгоритмом [5] по команде [9]

net1 = train(net,P,T).

В качестве вектора входа P задаются обучающие выборки (примеры обучающих контрольных и тестовых выборок для оценки 4+ приведены в табл. 5) из произвольного числа статистик, реа- лизующие все возможные оценки 12-балльной шкалы с соответствующими значениями целей T (желаемые результаты на выходе).

После завершения обучения проводится контрольное моделирование: на вход сети подаются контрольные и тестовые статистики (табл. 5), реализующие те же оценки. Если сеть правильно связывает типовое воздействие на входе с эталонны- ми значениями сигнала на выходе, то ИНС считается обученной.

После прохождения тестирования обучаемому выставляется оценка его знаний по 12-балльной шкале, которую также можно рассматривать как нечеткую [11].

СПЕЦИАЛЬНЫЕ НЕЙРОННЫЕ СЕТИ В КОНТРОЛЬНОМ ТЕСТИРОВАНИИ О-Н

Значительно бόльшую трудность для автоматизации, нежели рассмотренное выше тестирование закрытого типа (когда тестируемым производится выбор из фиксированного множества вариантов ответа), представляет тестирование открытого типа, когда тестируемый сам генерирует ответ.

Ответом на вопрос является [4] некоторое размышление, представленное в рукописном виде, это может быть изображение, формула или ее элемент, фрагмент текста или текст в целом.

Мы рассматриваем тестирующую нейронную сеть, когда у нее на входе в качестве решения ТЗ испытуемым присутствует рисованное изображение.

Использование при решении данной задачи нейросетевого подхода предполагает получение и последующее предоставление на вход сети обучающих, контрольных, тестовых примеров с последующей заменой на реальную информацию, в виде некоторого изображения. Таким образом, поставленную перед ИНС задачу можно формализовать и описать следующим образом: сеть должна распознавать входное изображение, детектировать его (находить определенные признаки или их отсутствие на изображении) и классифицировать изображение по наличию тех или иных признаков на "правильное" и "неправильное".

Рассматриваемую проблему автоматизации тестирования мы, таким образом, расширяем, присоединяя обширнейшую область знаний, именуе- мую "машинное распознавание изображений" (до настоящего времени не получившую канонического решения), одной из ветвей которой являются многочисленные попытки (с классических работ Ф. Розенблатта 50-х гг. минувшего века) разрешить задачу с помощью подходяще организованных нейронных сетей.

Поэтому в наших целях требовалось сделать выбор в пользу того или иного распознавателя изображений на входе нашей ИНС. И из соображений методического единства мы выбрали так называемые сверточные искусственные нейронные сети (СИНС), предложенные ЛеКуном [13]. Последние обеспечивают частичную устойчивость к изменениям масштаба, смещениям, поворотам, смене ракурса и другим искажениям изображения [14].

Используемая сеть состоит из шести слоев. Ее входными данными являются изображения (в качестве примера выбрано изображение размером 32×36 пикселей), которые классифицируются как "Наличие объекта" или "Отсутствие объекта". Так как задача, решаемая СИНС, — дихотомия, то для решения достаточно одного выхода. Выходное значение сети находится в интервале [–1; 1], что соответственно означает отсутствие или присутствие объекта на классифицируемом изображении.

При обучении сети в качестве учебного набора (рис. 3) используется коллекция изображений, полученных по результатам тестирования групп студентов Санкт-Петербургского государственного университета аэрокосмического приборостроения при изучении предметной области дисциплины "Бортовые вычислительные комплексы навигации и самолетовождения" [15]. В процессе подготовки обучающих, контрольных и тестовых статистик не выполнялось какой-либо нормализации изображений (выравнивания гистограммы или коррекции яркости). Для создания большого количества примеров и увеличения инвариантности

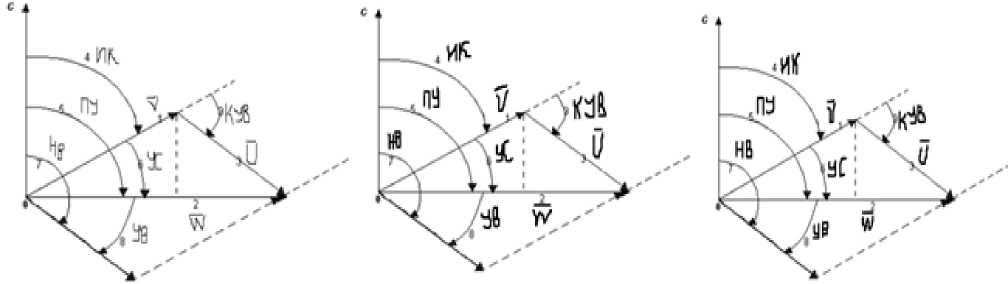
Рис. 3. Учебный набор из обучающих, контрольных и тестовых статистик

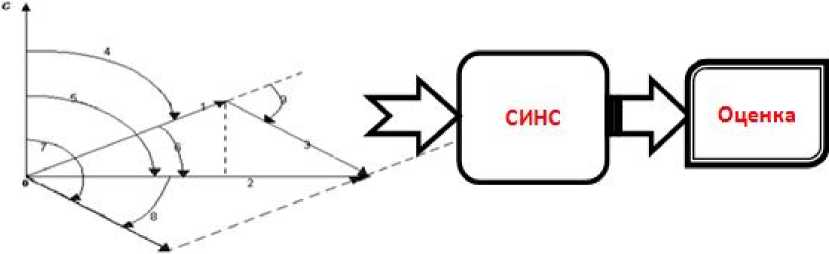
Рис. 4. Процесс тестирования

авторами [14] предлагается использовать ряд преобразований, включая отражение, вращение до ±360°.

Процесс тестирования происходит следующим образом (см. рис. 4). Обучаемому предоставляется возможность ответить на вопросы ТЗ открытого типа, например указать недостающие элементы навигационного треугольника скоростей, его ответы предоставляются СИНС как вектор входных данных. Сетью производится анализ полученных результатов. После прохождения тестирования обучаемому выставляется оценка его знаний по системе зачет/незачет или по классической 4балльной шкале (5, 4, 3, 2).

Таким образом, очевидно, что использование ИНС [5] позволяет осуществлять автоматизированный, интеллектуальный контроль знаний специалиста, использовать широкую номенклатуру сценариев обучения (ТЗ закрытого и открытого типа, АТ) и шкал оценивания от классических [6] до нечетких [12].