О применении свойств геликоиды в рубительных дисках

Вопросы применения свойств различных геометрических поверхностей при конструировании дисков ру-бительных машин рассматривались в ряде работ еще в 60–80-е годы прошлого столетия [1, 2].

Ранее нами в работах [3, 4] доказана целесообразность применения геликоидальной формы диска и заточки ножей в некоторых рубительных машинах. Было установлено, что в процессе рубки бревен между скоростями диаметрально противоположных точек бревна при его контакте с задней гранью ножа наблюдается кинематическое несоответствие. В результате этого бревна не занимают стабильного положения в процессе измельчения, что приводит к ухудшению качества фракционного состава производимой щепы.

Для устранения упомянутого кинематического несоответствия и обеспечения равномерности подачи бревна самозатягиванием необходимо обеспечить одинаковую скорость этого движения на любом радиусе резания и при любом угле поворота диска. Данные условия могут быть выполнены при применении геликоидальной поверхности диска и задней грани рубительных ножей.

Геликоидальная (винтовая) поверхность получается в результате сложного равномерного движения точки А (рис. 1), которая перемещается вдоль образующей поверхности цилиндра, в то время как сама образующая равномерно вращается вокруг оси цилиндра.

На практике для получения цилиндрической геликоидальной линии по данному диаметру основания цилиндра d, шагу винтовой линии Р, направлению вращения точки (по часовой или против часовой стрелки) и направлению поступательного движения точки (вверх или вниз) окружность основания цилиндра делят на любое количество равных частей (на рис. 1 – на двенадцать). Чем больше делений, тем больше точность выполняемых построений. Точки деления нумеруют по направлению движения точки, образующей геликоидальную линию (на рис. 1 – против часовой стрелки). Затем на контурной образующей цилиндра откладывают заданный шаг, который делят горизонтальными прямыми на то же количество равных частей; точки делений нумеруют снизу вверх.

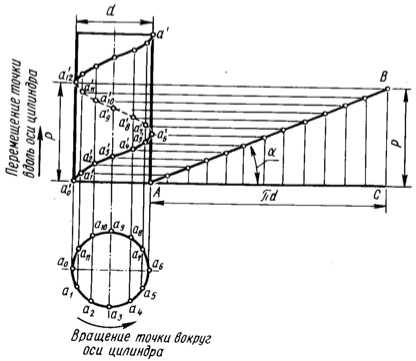
Рис. 1. Проекции геликоиды

Через точки деления окружности проводят вертикальные линии связи до пересечения с горизонтальными прямыми деления шага и получают точки а ₁', а ₂', а ₃', ..., принадлежащие фронтальной проекции геликоиды, затем соединяют их кривой при помощи лекала.

Фронтальная проекция цилиндрической геликоиды представляет собой синусоиду с длиной волны, равной шагу Р , и амплитудой, равной радиусу окружности основания образующего цилиндра.

Развертка части цилиндрической поверхности, ограниченной геликоидой на длине одного витка, представляет собой прямоугольный треугольник ABC (рис. 1), гипотенуза которого АВ – развертка витка геликоиды, больший катет АС – развертка окружности основания цилиндра, равная n d, и меньший катет ВС – шаг Р.

Из прямоугольного треугольника ABC (рис. 1) можно найти зависимость шага Р от угла подъема а гели- коиды (равен углу наклона гипотенузы АВ к катету АС):

P tg ^a = —-.                       (1)

nd

При проектировании дисковых рубительных машин с профилированной рабочей поверхностью возникает необходимость в расчете углов между плоскостью, перпендикулярной к оси вращения, и собственно рабочей поверхностью (далее «угол обнижения»). Для обеспечения стабильного качества щепы необходимо, чтобы эти углы обеспечивали одинаковое перемещение измельчаемой древесины на любом удалении от центра вращения диска во время рубки. Обеспечить это можно только в случае изготовления рабочей поверхности под переменным углом по отношению к плоскости вращения. В этом случае если накладка диска является продолжением задней грани ножа, то угол обнижения совпадает с задним углом ножа. При этом надо помнить, что минимальное значение этого угла должно быть не менее 2 ° , а максимальное должно обеспечивать требуемую прочность лезвия ножа.

Рассмотрим схему межножевого сектора, представленную на рисунке 2. На схеме изображен фрагмент диска, вращающегося против часовой стрелки. Линии a1б1 и a3б3 изображают лезвия ножей, а линия a2б2 – заднюю кромку накладки, где заканчивается профилированная рабочая поверхность. Радиусы r и R обозначают соответственно радиусы, на которых располагаются наиболее приближенная и наиболее удаленная точки лезвия режущего ножа (в данном случае начала профилированной поверхности).

Накладка б плане

Величину угла обнижения у min , рабочей поверхности ротора (задней грани ножа и накладки) на периферии определим, воспользовавшись изображением на рисунке 3:

h

Y min = arctg — ,              ⁽²⁾

a1a2

где h – величина возвышения режущей кромки ножа над задней кромкой накладки (рабочей поверхности

О диска); a1a2 – длина дуги, описываемой радиусом

R межу точками a₁ и a₂ .

Величина h возвышения режущей кромки ножа над задней кромкой накладки (рабочей поверхности диска):

h = lw sin а ,

щ

где а - угол между осью измельчаемого бревна и плоскостью вращения диска, измеренный в вертикальной плоскости; l – длина щепы.

щ

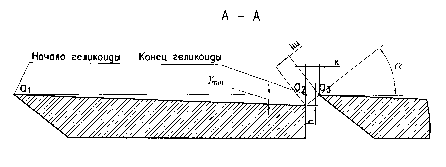
Рис. 3. Сечение рабочей поверхности по дуге a1a3 (нож не выделен)

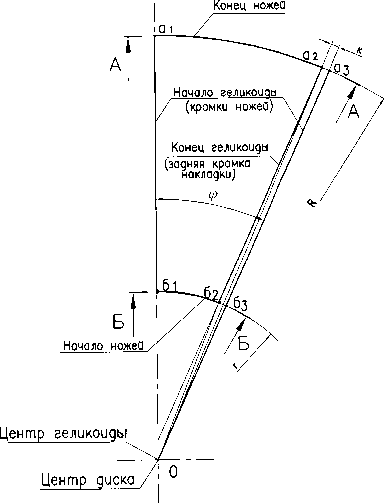
Рис. 2. Схема межножевого сектора с ножом (вид сверху)

Длину дуги межу формуле:

о

a1a2

Величину Z a ^ Oa ^

точками a₁ и a₂ определим по

nR / П

= ZaOa?.

180 1 2

определим из соотношения

Za1Oa2 = Za1Oa3 - Za2Oa3 .

Величину Z a₁Oa₃ определяем как:

Z a3Oa3 —     ,

nн где nн – количество ножей на диске.

Величину Z а₂0а з определим из соотношения: ^k

Za2Oa3 = arcsinR,

где k – расстояние от режущей кромки ножа до задней кромки накладки в плане.

Величина k определяется по формуле:

k = Lu cos а .

щ

Подставив все значения величин из выражений (3)– (8) в формулу (2), получим окончательное выражение для Y min :

На основании полученных уравнений можно вывести общее выражение для вычисления угла обнижения в любой точке, лежащей на прямой a ₁ б ₁:

Y min = arctg

lln sin a

щ

nR ( 360      .L ^{cos a}

---I-- arcsin —-----

180 1 n             R

н

, (9)

Y_i = arctg

L„ sin a

щ

где n_н – количество ножей на диске.

nr, ( 360       . lc ^{cos a}

—-1-- arcsin—----

180\ Пц             r нi

Для расчета угла обнижения на дуге, наиболее приближенной к центру вращения диска рубительной машины (см. рис. 4):

где Y_i — текущий угол обнижения; r_i - радиус, характеризующий положение точки на режущей кромке ножа

Y min

= arctg----7---- nr | 360

Т8Ю I " n T

н

L, sin a

щ

1 щ cos a

- arcsin —----- r

. (10)

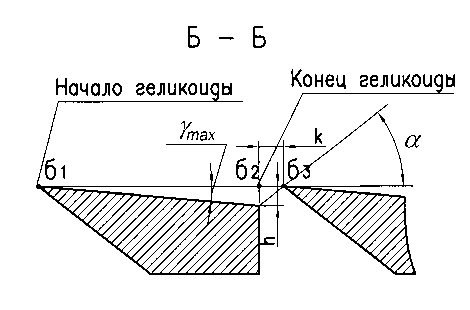
Рис. 4. Сечение рабочей поверхности по дуге б ₁ б ₃ (нож не выделен)