О применимости модели локального взаимодействия для определения сил сопротивления внедрению сферы в нелинейно-сжимаемый грунт

Методы локального взаимодействия, получившие развитие в задачах аэродинамики [1–3], находят применение и при исследовании движения тел в грунтовых средах [4–6]. При этом среди соотношений для напряжений, действующих на поверхности контакта тела и среды, наиболее часто используется двучленная модель взаимодействия, содержащая динамическую составляющую, квадратичную по скорости, с постоянным слагаемым, характеризующим прочность среды. Для сыпучих грунтовых сред, например, песчаных грунтов, прочностное слагаемое в законе сопротивления мало, но присутствует линейный по скорости член, обусловленный наличием внутреннего трения. Также из литературы известно, что движение затупленных тел вращения в сыпучем грунте сопровождается кавитацией [7], и для учета влияния этих эффектов необходимо применять численные методы. В данной работе проведено исследование нестационарных процессов удара и проникания жесткой сферы в нелинейно-сжимаемый грунт, описываемый известной ударной адиабатой, с учетом поверхностного и внутреннего трения грунта с целью оценки применимости моделей локального взаимодействия .

2.    Задача расширения сферической полости

Рассмотрим решение одномерной задачи расширения сферической полости в грунтовой среде [8, 9] от нулевого радиуса с постоянной скоростью U , применяемое в дальнейшем для определения параметров модели локального взаимодействия. Система уравнений пластического деформирования грунтовой среды включает уравнения неразрывности и изменения количества движения в эйлеровых переменных при условии сферической симметрии. Сжимаемость грунта характеризуется ударной адиабатой, представляемой линейной зависимостью скорости ударной волны c от массовой скорости U за ее фронтом: c = A + X U . Здесь константа A характеризует скорость распространения волны сжатия в грунте при малых давлениях, а λ — предельную сжимаемость грунта.

Сопротивление грунтовой среды сдвигу опишем линейной зависимостью предела текучести σ _T от давления p :

G T = Y + кр .

Соотношение (1) в условиях одноосного деформирования с учетом сферической симметрии может быть представлено в эквивалентном виде: g T = g₀ + pG, где g — радиальная компонента тензора напряжений Коши (принимается положительной при сжатии) [10]. Коэффициенты Y и σ₀ определяют сцепление, а κ и μ — внутреннее трение грунта в рамках модели Григоряна и связаны между собой соотношением p = к/(1 + 2к/3). Значения коэффициентов внутреннего трения, как показано в работах [11, 12], изменяются в диапазонах к = 0 + 1,5 и, соответственно, p = 0 + 0,75.

Напряжения σ на границе расширяющейся сферической полости, в зависимости от коэффициента внутреннего трения, определяются выражениями, полученными, аналогично [8], в предположении несжимаемости среды за фронтом ударной волны:

G = gt+ р U2 C .

Здесь:

GT

- 2 G ₀ln s ,        p = 0;

= < 2 g o ( 1 -s^{- 1} ) ,

p = 0,5;

( 3/2 -s-s 4/2 ) ,      p = 0;

C = <* ( 1/3 - 2ln s-s 3/3 ) , p = 0,5

G o ( 1 ^^Р )

P

3        2 p + 1 p- 1    .

--1--- s---s . ( p- 2)(2 p- 1) 2 p- 1 p- 2

р = р₀ /(1 - e³ ) — плотность за фронтом ударной волны, распространяющейся со скоростью c = Х^1/3 U + А/ 3

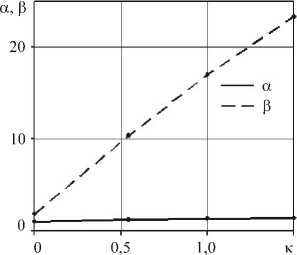
Рис. 1. Зависимости параметров квадратичной МЛВ от коэффициента внутреннего трения

в среде с начальной плотностью р₀; e = U/c . Сравнение с результатами численных расчетов напряжения σ на границе полости показало, что в диапазоне изменения коэффициента внутреннего трения грунта 0 < к <  1,5 и скоростей расширения полости U/А >  0,3 ошибка формул (2) убывает с ростом скорости, не превышая 5%.

В соответствии с моделью локального взаимодействия, напряжения, действующие на контактную поверхность тела в направлении нормали, могут вычисляться непосредственно по формулам (2) в предположении, что величина U равна нормальной компоненте вектора скорости тела, либо аппроксимироваться квадратичной зависимостью вида:

g/p₀ = a U ² + в U .

В выражении (3) пренебрегаем величиной сцепления аналогично закону проникания в форме Резаля [7, 13].

На рисунке 1 показано поведение параметров α, β , входящих в выражение (3), в зависимости от коэффициента внутреннего трения κ , определенных путем аппроксимации результатов (2) методом наименьших квадратов. Как видно из графика, параметр α изменяется незначительно, а параметр β при линейном слагаемом увеличивается с ростом коэффициента внутреннего трения κ . Экспериментальные данные [7, 14] свидетельствуют, что в грунтовых средах коэффициент к ® 1, таким образом, при решении задач проникания в грунтовые среды влияние параметра β может оказаться значительным.

3.    Результаты осесимметричных численных расчетов

Численное моделирование поведения геоматериалов (грунтов и горных пород) при действии взрывных и ударных нагрузок в осесимметричной постановке на основе явных конечно-разностных схем проводилось ранее в работах [6, 15–18]. В данной работе постановка задачи моделирования нестационарных процессов удара и проникания жесткой сферы в нелинейно-сжимаемый грунт соответствует постановке, используемой в работе [6], а решение задачи проводится в рамках численной методики [15, 19, 20], основанной на модифицированной схеме Годунова и реализованной в пакете прикладных программ НИИМ ННГУ «Динамика 2» [21]. Расчеты в осесимметричной постановке проводились при следующих значениях параметров [22], отвечающих сухой песчаной смеси естественного состава: A = 460м/с; X = 2,3; р0 = 1700 кг/м3; Y = 0,01 МПа; к = 1; радиус ударника составлял R = 0,01 м. Подобласть грунта покрывалась разностной сеткой с квадратными ячейками, размеры сторон которых при численном исследовании сходимости решений принимались равными Rn. Рассматривались варианты сетки при n = 45,90,135 и 180. Серия численных расчетов показала, что применение схемы первого порядка точности [19, 20] обеспечивает сходимость в зависимости от шага сетки, близкую к линейной сходимости результатов численных расчетов (при силах сопротивления на квазистационарной стадии внедрения сферы в грунт со скоростью V0 = 400 м/с), и в данной нестационарной задаче проникания. Величина шага, определенная при n = 90, выбиралась в дальнейшем как базовая для проведения расчетов и приводила к погрешности не более 5%.

Результаты расчетов проникания сферического ударника в грунт с постоянной скоростью внедрения 300 м/с содержит рисунок 2. Кривые 1 – 4 (Рис. 2, а ) — это расчетные распределения вдоль поверхности ударника безразмерных нормальных напряжений при к = 0 в безразмерные моменты времени V ₀ t/R , которым на рисунке 2, б отвечают точки 1 – 4 . Аналогично, на рисунках 2, в , г показаны данные расчетов при к = 1. Кривые 5 , 6 получены в рамках модели локального взаимодействия с применением формул (2) и некой модификации, которая будет описана далее. Напряжения отнесены к величине скоростного напора q = р₀ V ₀².

Площади, ограниченные кривыми распределения напряжений, соответствуют значениям безразмерной силы сопротивления внедрению, изображенной на рисунке 2, б , г , в зависимости от безразмерного времени

z zS

— = -[° n dz ² = ^dS , qS 0     -1 q 0 q

F =- 2 S 0 J о „ zdz ,

-1

где S ₀ = n R ² — площадь миделя (наибольшего по площади поперечного сечения тела); S = 1 - z ² — текущая площадь поверхности контакта тела и среды; z =- 1 + V ₀ t/R ; - 1 <  z <  0 . Точки 1-3 отвечают временному интервалу, когда сила сопротивления достигает своего максимального значения; в момент времени, соответствующий точке 4 , устанавливается квазистационарное значение силы. Аналогичные результаты получены для скоростей из диапазона 0,5 <  V ₀ / A <  1,5 при коэффициентах внутреннего трения 0 <  к <  1,5 .

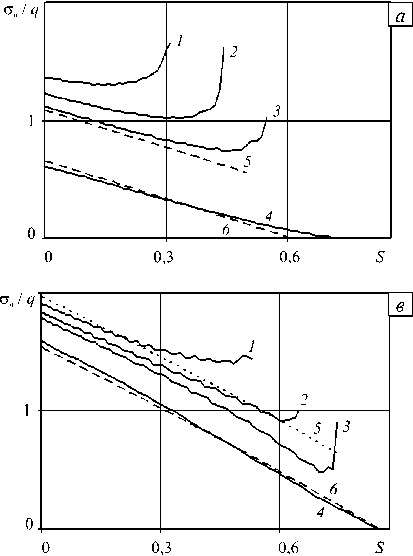
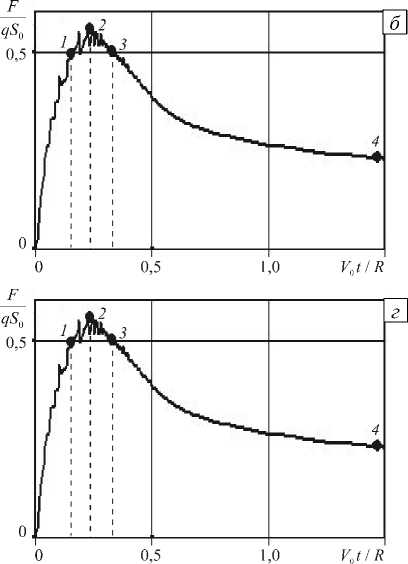
Рис. 2. Результаты расчетов проникания сферического ударника в грунт с постоянной скоростью внедрения 300 м/с при к = 0 ( а, б ) и к = 1 ( в, г )

Усредненные значения безразмерных нормальных напряжений, полученные численно для различных коэффициентов внутреннего трения, приведены на рисунке 3 в зависимости от площади поверхности 1z контакта   F/( о MS0 ) = -    | о ndz2 ® cj nS ,   S = 1 - z 2,   о M ® 2р0 (A + X V) V0 / 3. В представленных

° M -1

координатах наблюдается близкое к линейному падение значений напряжений, причем скорость падения, отражаемая наклоном кривых, обратно пропорциональна коэффициенту внутреннего трения. Точки на рисунке соответствуют моментам формирования максимума силы сопротивления и отрыва потока.

В целом по результатам расчетов можно отметить, что значения напряжений, определенные в моменты достижения силой сопротивления внедрению максимального значения, удовлетворительно отображаются моделью локального взаимодействия в форме (3) с параметрами, найденными на основе (2). Для описания квазистационарных значений предлагается модифицировать (2), добавив постоянное слагаемое σ* (с обратным знаком), равное напряжению в точке отрыва потока:

о '/р₀ = ( о - о * ) /р₀ = a V ₀ ² ( cos² ф - cos² ф * ) + в V₀ ( cosф - cosф * ) ,                     (5)

где cosф = - z , при этом угол ф отсчитывается от вершины сферы. В соотношениях (5) ф * является свободным параметром, который подбирается из условия наилучшего соответствия численным результатам. Проведенные расчеты показали, что значения параметра φ^* при изменении коэффициента внутреннего трения в диапазоне 0 < к <  1,5 близки к значениям угла отрыва потока. Показанные на рисунках 2, а, в кривые 6 отвечают зависимостям нормального напряжения, вычисленного по формуле (5). Рисунок демонстрирует их близость к соответствующим расчетным напряжениям (кривые 4 ).

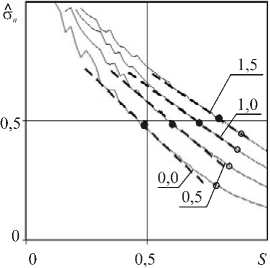
Рис. 3. Безразмерные нормальные напряжения в зависимости от площади поверхности контакта для значений κ (•, ○ – значения, отвечающие максимуму силы сопротивления и отрыву потока)

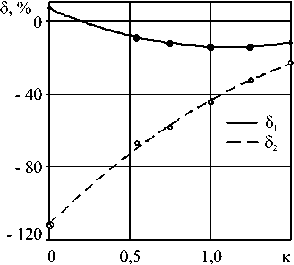
Рис. 4. Погрешности определения максимума ( δ ₁ ) и квазистационарного значения ( δ ₂ ) силы сопротивления в рамках модели локального взаимодействия (точки и аппроксимирующие их кривые) относительно численных расчетов

Интегрирование напряжений по формуле

* z

F = - 2 S о |

-1

* φ оnzdz = 2S0 |

σ _n cosφsinφ d φ

с использованием

для σ _n выражений (3) и (5) дает возможность определить максимум силы сопротивления и значение на квазистационарной стадии внедрения. Погрешности вычисления этих величин, соответственно δ₁ и δ₂ , относительно результатов осесимметричных численных расчетов показаны на рисунке 4 точками и аппроксимирующими их кривыми (сплошная линия соответствует погрешности δ₁ , штриховая — δ₂ ). Применялась модель (3) с параметрами, рассчитанными на основе (2), как для определения максимальных, так и квазистационарных значений силы сопротивления. Штриховая линия в данном случае фактически отражает уменьшение отношения максимальных и квазистационарных значений с ростом коэффициента внутреннего трения.

4.    Анализ влияния трения на силу сопротивления внедрению сферы

Рассмотрим далее задачу проникания сферы в грунт при учете поверхностного трения в соответствии с законом Кулона: с_т = k mp с _n , где к тр — коэффициент сухого трения. На рисунке 5, а приведены зависимости нормальных (кривые 1 , 2 ) и тангенциальных (кривые 3 , 4 ) напряжений от угла φ

а

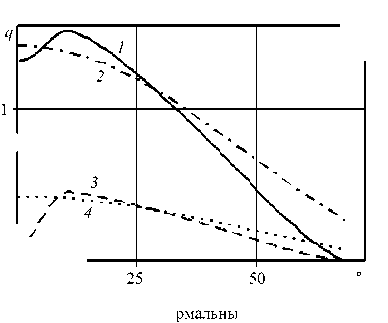
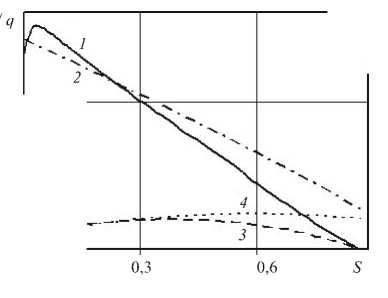
Рис. 5. Зависимости нормальных (кривые 1, 2 ) и тангенциальных (кривые 3 , 4 ) напряжений от угла φ на квазистационарной стадии внедрения ( а ) и их проекции на ось вращения сферического ударника ( б )

на квазистационарной стадии внедрения ударника. Кривые 1 , 3 получены численно с использованием пакета «Динамика 2», кривые 2 , 4 — по формуле (5). В численных расчетах применялся смешанный закон трения [23], что привело к различию в напряжениях на ранней стадии внедрения (см. Рис. 5, а ). Однако отличия у проекций напряжений на ось вращения (Рис. 5, б ), необходимых для нахождения интегральной силы сопротивления внедрению, проявляются существенно меньше. В приведенных координатах площади под кривыми определяют вклады соответствующих компонент напряжений в результирующую силу сопротивления на квазистационарной стадии внедрения сферы в грунт.

Сила сопротивления внедрению ударника с учетом сухого трения находится следующим образом [5]:

F = - 2 S 0 J ( g n z + g _t V1 - z ² ) dz = 2 S ₀ J ( g n cosф + o _T sinф ) sin ф d ф . -1^x                                                 0

На основе моделей локального взаимодействия (3) и (5) интеграл (6) можно вычислить явно. В результате получаются следующие выражения для коэффициентов квадратичной зависимости силы сопротивления внедрению сферы от скорости удара V ₀ :

Ff ( P o S о ) = AV 02 + BV o ,

A = a( A + k mp A ₂),        B = PC B 1 + k mp B 2 ),

где коэффициенты A_k , B_k для максимального значения силы сопротивления рассчитываются по формулам:

A 1 = ( 1 - cos⁴ ф ) /2, A ₂ = ( ф- 2sin ф cos³ ф + sin ф cos ф ) /4, B 1 = 2 ( 1 - cos³ ф ) /3,    B ₂ = 2 sin³ ф /3 .

Аналогично, с использованием (5), получаем значения коэффициентов силы сопротивления (7) на квазистационарной стадии внедрения:

A , = ( 1 - cos² ф ) ^2, A 2 = ( 2sin ф cos³ ф + sin ф cos ф- 4 ф cos² ф + ф ) /4, B 1 = ( cos³ ф- 3cos ф + 2 ) /3 , B ₂ = ( 2sin³ ф + 3cos² ф sin ф- 3 ф cos ф ) /3,

где ф — определенный ранее угол отрыва потока (символ « * » в обозначении опущен).

На рисунке 6 приведены δ₁ и δ₂ — погрешности результатов вычислений по модели локального взаимодействия (3) и (5) относительно результатов численных расчетов (на рисунке показаны точками и аппроксимирующими их кривыми) силы сопротивления внедрению жесткой сферы в песчаный грунт при коэффициенте сухого трения к_тр = 0,3 . Сплошная и штриховая линии соответствуют максимальному и квазистационарному значениям, вертикальные линии с засечками означают диапазон изменения δ₁ и δ₂ при варьировании скоростей внедрения в осесимметричных численных расчетах от 300 до 600 м/с.

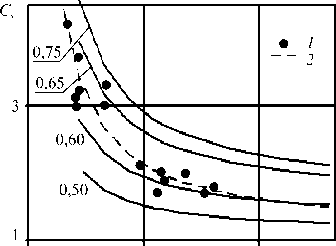
На рисунке 7 показаны значения коэффициента сопротивления внедрению сферы в песчаный грунт Cx = 2 F/qS ₀ в сравнении с данными обращенного эксперимента [14]. Наблюдается хорошее соответствие

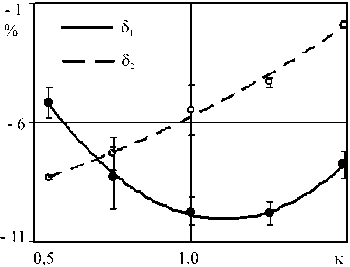
Рис. 6. Погрешности определения максимума ( δ ₁ ) и квазистационарного значения ( δ ₂ ) силы сопротивления в рамках модели локального взаимодействия с учетом трения (точки и аппроксимирующие их кривые)

О             0,5              1,0 VIA

Рис. 7. Значения коэффициента сопротивления внедрению сферы в песчаный грунт, полученные по формулам (2), (5), (9) при различных значениях коэффициента внутреннего трения грунта ц (сплошные линии) и данные эксперимента (точки 1 и аппроксимирующая их кривая 2 )

экспериментальных данных и данных по модели локального взаимодействия, полученных на основе формул (2), (5), (9), при k mp = 0,45 и коэффициенте внутреннего трения р = 0,6 + 0,65 (к = 1,0 + 1,2).

5.    Анализ применимости модели локального взаимодействия на основе волнового механизма формирования силы сопротивления

Как показано на рисунках 2, а , в , нормальные напряжения на контактной поверхности проникающей сферы изменяются от максимального значения, достигаемого в момент удара, до некоторого квазистационарного значения, устанавливающегося после отрыва потока грунта с боковой поверхности сферы. Скорость падения напряжений при этом пропорциональна коэффициенту внутреннего трения (Рис. 3) и максимальна при к = 0. Вследствие этого отношение максимума силы сопротивления к квазистационарному значению также увеличивается при уменьшении коэффициента внутреннего трения (Рис. 2, б , г ).

Полученные результаты находят объяснение в рамках предлагаемого далее волнового механизма формирования силы сопротивления внедрению затупленного тела вращения. Напряжения ° n ~ Р₀ ( A + ^ V n ) V n , где V n =- V) z , возникающие на контактной поверхности ударника в момент удара, далее за счет волнового взаимодействия с полупространством грунта уменьшаются в направлении, перпендикулярном нормали. Интенсивность данного взаимодействия определяется скоростью ударной волны c ( V n ) и внутренним трением. Коэффициент внутреннего трения к (см. (1)) в условиях одноосной деформации может быть определен, если известен коэффициент бокового давления K _σ , равный отношению радиального и продольного напряжений K _а = 1 -ц = ( 1 -к/ 3 )/( 1 + 2 к/ 3 ) [7].

Различия в скоростях падения напряжений и увеличения контактной поверхности приводят к тому, что максимум силы сопротивления наблюдается раньше, чем наступает отрыв потока, то есть сила сопротивления убывает при одновременном расширении контактной поверхности ударника. Это предположение подтверждается данными расчетов с коэффициентом внутреннего трения к = 0 (Рис. 2, а ) и результатами экспериментально-теоретического анализа процессов проникания сферы в песчаный грунт, выполненного в [24]. С ростом κ моменты времени достижения максимума силы сопротивления и отрыва потока сближаются. Изменение скорости удара в диапазоне 0,5 <  V₀ / A <  1,5 незначительно влияет на угол срыва потока, который составляет 60° + 70° при изменении коэффициента внутреннего трения в диапазоне 0 + 1,5 .

С течением времени от момента удара в окрестности головной части ударника за счет волнового воздействия в поперечном направлении устанавливается напряженное состояние, приближенное к одномерному, что объясняет невысокую (от +10 до –15%) погрешность применения одномерной модели локального взаимодействия. Смена знака погрешности определения максимума силы сопротивления внедрению сферического ударника в рамках модели локального взаимодействия при к ® 0,25 объясняется влиянием отошедшей ударной волны, увеличивающимся с убыванием κ и в наибольшей степени проявляющимся при к = 0 .

Слабая зависимость полученных результатов (отношений максимальных и квазистационарных значений силы, погрешностей модели локального взаимодействия) от скорости внедрения, по-видимому, связана с достаточно высоким значением параметра предельной сжимаемости X = 2,3 в ударной адиабате песчаного грунта, взятой в качестве примера. Это обеспечивает режим обтекания ударника с отошедшей ударной волной, по крайней мере, при 0,5≤V0 A≤1,5. При значениях λ ≈ 0,5 и сверхзвуковых скоростях внедрения V0 A≥ 1 отношение максимальных и квазистационарных значений силы сопротивления внедрению сферы приближается к единице.

Полагаем, что дальнейшее падение напряжений связано с кавитационными эффектами отрывного обтекания. С момента удара в окрестности головной части затупленного ударника формируется поле скоростей, направленное вдоль свободной поверхности среды, что приводит к дополнительному уменьшению напряжений, действующих на поверхность проникающего тела, до некоторых квазистационарных значений после отрыва потока. Таким образом, наблюдается влияние формы ударника в окрестности лобовой точки на распределение напряжений вдоль образующей тела, что противоречит исходным предпосылкам одномерных моделей локального взаимодействия и объясняет высокую ошибку, имеющую место при определения силы сопротивления сферы на квазистационарной стадии внедрения. Заметим, что значения силы сопротивления на данной стадии внедрения обуславливаются преимущественно параметрами процесса проникания тела конечной массы в грунт. Критерием применимости моделей локального взаимодействия в этом случае может служить величина отношения максимального и квазистационарного значений силы сопротивления внедрению сферы в грунт. Увеличение данной характеристики с ростом скорости сферического ударника показано экспериментально в [24] и связывается с увеличением коэффициента бокового давления грунта, а, следовательно, и большим влиянием эффектов волнового взаимодействия в поперечном направлении.

6.    Заключение

Проведено исследование применимости модели локального взаимодействия на основе численных расчетов процесса удара и проникания жесткой сферы в песчаный грунт с постоянной скоростью внедрения при изменении коэффициента внутреннего трения в допустимом диапазоне 0 ≤κ≤ 1,5 . Показано, что погрешность при расчете максимума силы сопротивления по модели локального взаимодействия на основе решения задачи расширения сферической полости составляет от +10 до –15%, а ошибка определения квазистационарного значения силы может превышать 100% при κ = 0 и 15% при κ = 1,5 . Предложен механизм формирования силы сопротивления, качественно отвечающий результатам экспериментов и расчетов внедрения сферы в нелинейный грунт с учетом внутреннего и поверхностного трения. Механизм может быть распространен и на тела другой формы.

Авторы благодарят профессоров В.Г. Баженова и А.М. Брагова за внимание к работе и представление отдельных результатов данной статьи на XVIII Международном симпозиуме им. А.Г. Горшкова «Динамические и технологические проблемы механики конструкций и сплошных сред».

Работа выполнена при поддержке Министерства образования и науки Российской Федерации в рамках реализации ФЦП «Научные и научно-педагогические кадры инновационной России» на 2009-2013 гг. (соглашение 14.132.21.1361), Совета по грантам Президента РФ для ведущих научных школ (грант НШ-2843.2012.8) и РФФИ (проекты № 10-08-00376-а, 12-05-1075-а, 12-08-33106-мол_а_вед).