О применимости тензорного метода стоимостного анализа сетей интегрального обслуживания
Автор: О. В. Колмаков, М. Н. Петров
Журнал: Informatics. Economics. Management - Информатика. Экономика. Управление.
Рубрика: Системный анализ, управление и обработка информации
Статья в выпуске: 2 (3), 2023 года.
Бесплатный доступ
Статья посвящена исследованию возможностей применимости тензорного метода стоимостного анализа сетей интегрального обслуживания. Анализ экономической эффективности процессов развития инфраструктуры сетей интегрального обслуживания показывает, что технологии интеграции телефонных служб в сети передачи данных являются востребованными из-за широких возможностей по уменьшению стоимости владения сетевыми инфраструктурами. Отмечается, что технологии мультисервисных сетей требуются первоначальных капиталовложения на модернизацию оборудования передачи данных для обеспечения должного качества обслуживания, установку интерфейсов взаимодействия внутри и вне сети, а также средств мониторинга и управления мультисервисной сетью. Показано, что реальные сети связи характеризуются большим числом узлов и имеют сложную архитектуру. Это затрудняет их аналитическое описание и использование методов, основанных на моделях теории массового обслуживания, случайных марковских процессов и теории вероятностей. В данной статье рассматривается возможность применения тензорной методологии к стоимостному анализу сетей интегрального обслуживания. В работе представлены полученные результаты применимости тензорного метода для стоимостного анализа сетей интегрального обслуживания. Полученные результаты доведены до инженерных расчетов, что позволило привести примеры расчетов конкретных топологий сетей.
Труктура сети, стоимостной анализ, интегральное обслуживание, тензорный метод, мультисервисная сеть
Короткий адрес: https://sciup.org/14127462
IDR: 14127462 | УДК: 621.3.063.8 (07) | DOI: 10.47813/2782-5280-2023-2-3-0210-0224
Текст статьи О применимости тензорного метода стоимостного анализа сетей интегрального обслуживания
DOI:
В настоящее время анализ развития инфраструктуры сетей интегрального обслуживания показывает, что технологии интеграции телефонных служб в сети передачи данных стали очень популярными, прежде всего из-за широких возможностей по уменьшению стоимости владения сетевыми инфраструктурами [1-4]. В результате такой интеграции отпадает необходимость содержать дополнительные сети, обеспечивающие передачу трафика реального времени. Следовательно, исчезают затраты, связанные с поддержанием и обслуживанием таких сетей (заработанная плата персонала, аренда каналов связи и так далее) [5]. Безусловно, на первых этапах перехода от традиционных телефонных технологий к технологиям мультисервисных сетей требуются первоначальные капиталовложения на модернизацию оборудования передачи данных для обеспечения должного качества обслуживания, установку интерфейсов взаимодействия с телефонной сетью, а также средств мониторинга и управления мультисервисной сетью [610].
Если еще не так давно отмечалось, что системы интегрированного широкополосного доступа нескоро приживутся в России, то сегодня очевидно широкое внедрение широкополосных систем (АТМ, Ethernet, Frame Relay, xDSL и т.д.).
Анализируя достоинства и недостатки той или иной технологии, ясно одно, что успех внедрения широкополосных систем будет зависеть от того, какое количество пользователей будет вовлечено в процесс использования новых технологий, от стоимости абонентского оборудования доступа, которое, в свою очередь, должно быть по карману массовым потребителям данной услуги [11].
МЕТОДЫ УВЕЛИЧЕНИЯ ДОХОДОВ
За прошедшее столетие архитектура телефонных сетей практически не изменилась, разве что алгоритмы сигнализации усложнились. Рост доходов от предоставления базовых телефонных услуг ограничен, поэтому телекоммуникационные операторы вынуждены искать новые источники доходов [5, 11].
Безусловно, внедрение новых технологий – процесс трудоемкий и дорогостоящий. По мнению специалистов, модернизировать, например, всю коммутационную систему не разумно, для обслуживания трафика новых услуг достаточно будет дооборудовать АТС мультисервисным узлом. К тому же это на порядок дешевле замены всего оборудования станции [12].
Одним из основных блоков мультисервисного сетевого узла (МСУ) является сетевой адаптер (рисунок 1), который должен обеспечить взаимодействие МСУ с любым коммутационным оборудованием, установленным на телефонной сети общего пользования (ТФоП). Это могут быть цифровые, координатные и даже декадно-шаговые АТС. Помимо сопряжения с АТС, узел МСУ должен решать еще ряд важных задач. К ним относится: подключение к ТФоП через интерфейс Ethernet пользователей с оконечными устройствами типа IP-телефонов; увеличение абонентской емкости АТС (через интерфейс Z); подключение существующих и новых абонентов АТС к услугам интеллектуальной сети (через пункт коммутации услуг - SSP).
Медиа-шлюз в составе МСУ является фактически шлюзом IP-телефонии и выполняет все свойственные ему функции. Это преобразование речевых/сигнальных сообщений в форматы, используемые в ТФоП и IP-сети, реализация физического интерфейса между этими сетями и тому подобное. Еще один элемент МСУ – блок взаимодействия IWF (Internet Working Function) – служит для доступа пользователей в сети АТМ и Frame Relay, а также Интернет. Структура МСУ может меняться в зависимости от решаемых задач. Так, в минимальной конфигурации он может выполнять только функции интегрированного с АТС узла интернет-доступа. Для крупных сетей, кроме узлов МСУ, целесообразно использовать так называемый сигнальный коммутатор (см. рисунок 2) [4].
МСУ
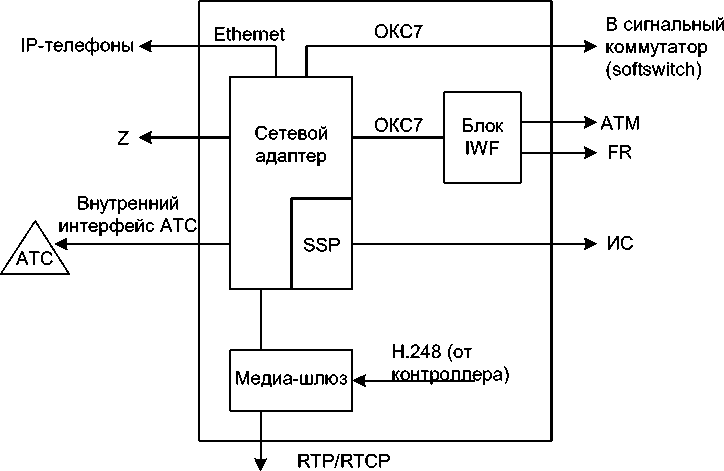
Рисунок 1. Структура мультисервисного сетевого узла.
Figure 1. Structure of a multiservice network node.
Сигнальный
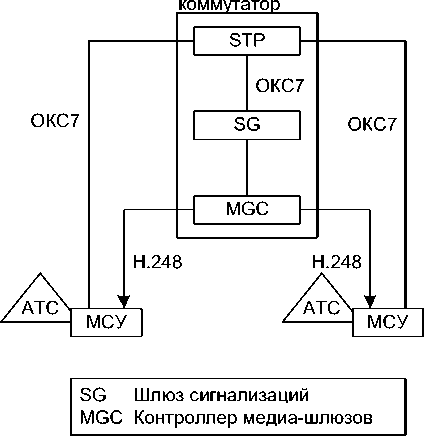
Рисунок 2. Вариант развертывания мультисервисных узлов с использованием сигнального коммутатора.
Figure 2. Variant of deploying multiservice nodes using a signal switch.
В состав сигнального коммутатора включен контроллер MGC (Media Gateway Controller), служащий для управления медиашлюзами. Причем, по мнению специалистов, для такого управления лучше использовать протокол H.248.
Сигнальный коммутатор может содержать также блок STP, назначение которого – обеспечить транзит сигнальных сообщений ОКС № 7 для оптимизации структуры сети сигнализации. Однако, использование STP целесообразно только на крупных ГТС, на сетях малой и средней емкости он не требуется.
В результате отметим основные тенденции при обеспечении роста доходов сетей интегрального обслуживания:
-
• технологии интеграции телефонных служб в сети передачи данных стали очень популярными;
-
• появление новых видов трафика происходит стремительно и в больших объемах;
-
• необходимо создавать интегрированные (мультисервисные) системы, предоставляющие широкий спектр услуг по передаче различных видов трафика;
-
• экономические проблемы остаются актуальными, о чем можно судить по многочисленным публикациям за последнее время.
РЕЗУЛЬТАТЫ ПРИМЕНИМОСТИ ТЕНЗОРНОГО МЕТОДА ДЛЯ СТОИМОСТНОГО АНАЛИЗА СЕТЕЙ ИНТЕГРАЛЬНОГО ОБСЛУЖИВАНИЯ
Все существующие на сегодняшний день современные технологии позволяют предоставлять широкий спектр услуг связи. Причем оборудование разных компаний во многом идентично по функциональным характеристикам. Различия начинают проявляться в деталях и, безусловно, многое зависит от стоимости оборудования, что в свою очередь влияет на стоимость сети в целом. Поэтому, развитие сетей с интеграцией служб зависит главным образом от платежеспособности спроса на современные услуги связи [13].
Среди проблем, связанных с концепцией построения сетей интегрального обслуживания, возникает потребность и в эффективных методах анализа систем и сетей связи. Реальные сети связи характеризуются большим числом узлов и имеют сложную архитектуру. Это затрудняет их аналитическое описание, даже если использовать современные методы, основанные на методах теории массового обслуживания, случайных марковских процессах и теории вероятностей.
В данной статье рассматривается возможность применения тензорной методологии к стоимостному анализу сетей интегрального обслуживания [14-18].
В данной работе предлагается использовать тензорный метод для стоимостного анализа и исследования сетей интегрального обслуживания. В качестве тензора выбрана формула определения стоимости узла коммутации.
S = N • и, (1)
где S - стоимость узла коммутации; N - число источников узла коммутации; и - удельная стоимость одного источника информации.
Рассмотрим конкретный пример. На рисунке 3 представлена сеть связи, состоящая из пятнадцати узлов.
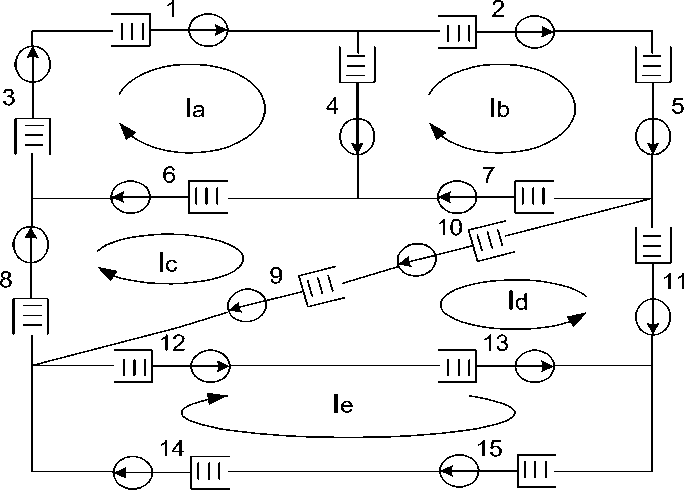
Рисунок 3. Исследуемая сеть.
Figure 3. Network under study.
Необходимо найти соотношение между суммарной стоимостью, числом источников и удельной стоимостью в сети для дальнейшего анализа с целью создания оптимальной топологии или при заданной топологии найти оптимальные затраты на оборудование узлов коммутации и самой сети. При тензорном анализе задача может решаться в обратном порядке, что является большим преимуществом данного метода, то есть имеется пятнадцать узлов с известными параметрами стоимости узла коммутации, числа источников и удельной стоимости одного источника, а необходимо найти оптимальную топологию сети.
Цифрами здесь и далее обозначены узлы коммутации интегральной информации.
Строчными латинскими буквами обозначены контуры. Контурные потоки не имеют явного физического смысла и приобретают его, суммируясь в ветви, по которой они
|
протекают. функции. |
Прописными латинскими буквами и греческими строчными обозначены u 1, N 1, S 1 u 2, N 2, S 2 u 3, N 3, S 3 u 4, N 4, S 4 u 5, N 5, S 5 u 6, N 6, S 6 u 7, N 7, S 7 u 8, N 8, S 8 u 9, N 9, S 9 u 10, N 10, S 10 u 11, N 11, S 11 u 12, N 12, S 12 u 13, N 13, S 13 u 14, N 14, S 14 u 15, N 15, S 15 Рисунок 4. Простейшая проекция пятнадцати узловой сети. Figure 4. The simplest projection of a fifteen-node network. |
Согласно методу тензорного анализа под пятнадцати узловой сетью понимается группа возможных комбинаций соединения узлов. Между различными проекциями существуют матрицы перехода. Поэтому можно получить решение для любой проекции, а затем с помощью известных формул перенести полученные результаты на другие проекции. При этом для получения результатов можно выбрать удобную (простую) проекцию, где меньше решений или они значительно проще.
Простейшая проекция пятнадцати узловой схемы, имеет такой вид: необходимо разнести узлы на бесконечное расстояние и рассмотреть каждый из них в отдельности (рисунок 4).
Для такой проекции имеется решение, оно простое и может быть представлено в виде матриц для всей сети в целом u =
u u2 u u4 u5 u6 u7 u8 u9 u10 u11 u12 u13 u14 u15
S 1
S 2
S 3
S 4
S 5
S 6
S 7
S 8
S 9
S 10
S 11
S 12
S 13
S 14
S 15
При этом сохраняется основное соотношение S = N ■ и.
В данном примере косвенное влияние между узлами коммутации отсутствует, поэтому все недиагональные элементы матрицы N равны нулю.
Тогда можно перейти к решению первоначальной проекции. Достаточно найти матрицу перехода. Для этого в исследуемой сети (рисунок 3) задаются новые удельные стоимости, число которых равно числу контуров в сети. Затем находятся соотношения между удельными стоимостями различных сетей.
|
N 1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
0 |
N 2 |
0 |
0 |
0 |
0 |
0 |
|
|
0 |
0 |
N 3 |
0 |
0 |
0 |
0 |
|
|
0 |
0 |
0 |
N 4 |
0 |
0 |
0 |
|
|
0 |
0 |
0 |
0 |
N 5 |
0 |
0 |
|
|
0 |
0 |
0 |
0 |
0 |
N 6 |
0 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
N 7 |
|
|
N = |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
N 8 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
N 9 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
N 10 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
N 11 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
N 12 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
N 13 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
N 14 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
N 15 |
|
u |
= u a , |
a |
b |
c |
d |
e |
|
u 2 |
= ub , "' |
1 |
0 |
0 |
0 |
0 |
|
u |
= u a , |
0 |
1 |
0 |
0 |
0 |
|
u 4 |
= u a - u b , |
1 |
0 |
0 |
0 |
0 |
|
u |
= u b , |
1 |
-1 |
0 |
0 |
0 |
|
u 6 |
= u a - u c , |
0 |
1 |
0 |
0 |
0 |
|
1 |
0 |
-1 |
0 |
0 |
||
|
u |
= u b - u c , |
|||||
|
0 |
1 |
-1 |
0 |
0 |
||
|
u 8 |
u c , C= |
|||||
|
0 |
0 |
1 |
0 |
0 |
||
|
u |
= u + u, , |
|||||
|
9 |
cd , |
0 |
0 |
1 |
1 |
0 |
|
u 10 |
= uc + ud , |
0 |
0 |
1 |
1 |
0 |
|
u 11 |
= - u d , |
0 |
0 |
0 |
-1 |
0 |
|
u 12 |
= u d + ue , |
0 |
0 |
0 |
1 |
1 |
|
u 13 |
= u d + u e , |
0 |
0 |
0 |
1 |
1 |
|
u 14 |
= u e |
0 |
0 |
0 |
0 |
1 |
|
0 |
0 |
0 |
0 |
1 |
||
|
u 15 |
= u e , |
Транспонированная матрица преобразования:
С Т
|
1 |
0 |
1 |
1 |
0 |
1 |
0 |
|
0 |
1 |
0 |
- 1 |
1 |
0 |
1 |
|
0 |
0 |
0 |
0 |
0 |
- 1 |
- 1 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
|
0 |
1 |
1 |
- 1 |
1 |
1 |
0 |
0 |
|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
Имея матрицу перехода С , можно перейти к первоначальной проекции. Для этого воспользуемся формулами, предложенными Г. Кроном [19].
S' = CT- S, (2)
N' = TT-N-C . (3)
Суммарные стоимости и число источников в контурах исходной системы:
- 1
5 ' = Ст • 5 =
- 1
- 1
- 1
0 x
S 1
S 2
S 3
S 4
S 5
S 6
S 7
S 8
S 9
S 10
S 11
S 12
S 13
S 14
S 15
5 1 + 5 з + 5 4
+ 56
52 - 54 + 55 + 57
- 5 6 - 5 7 + 5 8 + 5 9 + 5 10
5 9 + 5 10 - 5 11 + 5 12 + 5 13
5 12 + 5 13 + 5 14 + 5 15
X
|
N ' = CT • N • C = |
1 0 0 0 0 |
0 1 0 0 0 |
1 0 0 0 0 |
1 - 1 0 0 0 |
0 1 0 0 0 |
1 0 - 1 0 0 |
0 1 - 1 0 0 |
0 0 1 0 0 |
0 0 1 1 0 |
0 0 1 1 0 |
0 0 0 - 1 0 |
0 0 0 1 1 |
0 0 0 1 1 |
0 0 0 0 1 |
0 0 0 0 1 |
X |
||
|
N 0 |
0000 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
000 |
|||||
|
0 N |
0000 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
000 |
|||||
|
00 |
N 000 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
000 |
|||||
|
00 |
0 N 00 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
- 1 |
000 |
|||||
|
00 |
00 N 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
000 |
|||||
|
00 |
000 N |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
- 10 0 |
|||||
|
00 |
0000 |
N 7 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
- 1 0 0 |
|||||
|
00 |
0000 |
0 |
N 8 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
X |
0 |
0 |
100 |
||||
|
00 |
0000 |
0 |
0 |
N 9 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
110 |
|||||
|
00 |
0000 |
0 |
0 |
0 |
N 10 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
110 |
|||||
|
00 |
0000 |
0 |
0 |
0 |
0 |
N 11 |
0 |
0 |
0 |
0 |
0 |
0 |
0 - 1 0 |
|||||
|
00 |
0000 |
0 |
0 |
0 |
0 |
0 |
N 12 |
0 |
0 |
0 |
0 |
0 |
011 |
|||||
|
00 |
0000 |
0 |
0 |
0 |
0 |
0 |
0 |
N 13 |
0 |
0 |
0 |
0 |
011 |
|||||
|
00 |
0000 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
N 14 |
0 |
0 |
0 |
001 |
|||||
|
00 |
0000 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
N 15 |
0 |
0 |
001 |
|||||
|
N 1 + N з + N 4 + N 6 |
- N 4 |
- N 6 |
0 |
0 |
|
- N 4 |
N + N + N + N |
- N 7 |
0 |
0 |
|
- N 6 |
- N 7 |
N 6 + N 7 + N 8 + N 9 + Nю |
N 9 + N 1o |
0 |
|
0 |
0 |
N 9 + N 1o |
N 9 + N 10 + N 11 + N 12 + N 13 |
N 12 + N 13 |
|
0 |
0 |
0 |
N 12 + N 13 |
N 12 + N 13 + N 14 + N 15 |
Согласно постулату второго обобщения, уравнение состояния исходной сети,
записанное в матричной форме, имеет тот же вид, что и уравнение состояния простейшей сети, то есть:
5' = N • и' . (4)
Эквивалентная система уравнений состояния исходной сети:
S 1 + S з + S 4 + S 6 = ( N i + N з + N 4 + N 6 ) ■ u a - N 4 ■ u b - N 6 • uc
S 2 - S 4 + S 5 + S 7 =- N 4 ■ u a + ( N 2 + N 4 + N 5 + N 7 ) • u b - N 7 • u c
* - S 6 - S 7 + S 8 + S 9 + S 10 = - N 6 ■ u a - N 7 • u b + ( N 6 + N 7 + N 8 + N 9 + N 10 ) • u c + ( N 9 + N 10 ) • u d S 9 + S 10 - S 11 + S 12 + S 13 = ( N 9 + N 10 ) ■ u c + ( N 9 + N 10 + N 11 + N 12 + N 13 ) ■ u d + ( N 12 + N 13 ) ■ u e ^ S 12 + S 13 + S 14 + S 15 = ( N 12 + N 13 ) ■ u d + ( N 12 + N 13 + N 14 + N 15 ) ■ u e
Решение получившейся системы из пяти уравнений и пяти неизвестных не представляет большого труда [14].
ЗАКЛЮЧЕНИЕ
Таким образом, основные положения тензорного метода Г. Крона могут быть применены для стоимостного анализа сетей интегрального обслуживания. В работе представлен разработанный метод стоимостного анализа сетей интегрального обслуживания, для реализации и которого выведены и обоснованы основные соотношения для расчета стоимости узла коммутации в сетях с интеграцией служб. Полученные результаты доведены до инженерных расчетов, что позволило привести примеры расчетов конкретных топологий сетей. Отметим, что тензорный метод анализа может существенно упростить расчеты и обеспечить решение задач для сложных топологий сетей с большим числом узлов и связей между ними.


