О природе скачка коэффициента теплового расширения стекол при переходе жидкость-стекло

Симха и Бойер [1] для аморфных органических полимеров установили эмпирическое правило

A вTg - const - 0.1, (1) где А в = (e l — e g ) — скачок коэффициента объемного теплового расширения (КТР) при температуре стеклования T g , P l и P _g - КТР выше и ниже T_g.

Это правило оказалось справедливым не только для аморфных полимеров, но и для других стеклообразных систем, в частности, для низкомолекулярных неорганических стекол [2]. На рис. приводится схема типичной температурной зависимости удельного объема системы в жидком (1), переохлажденном (2), стеклообразном (3) и кристаллическом (4) состояниях. Здесь T f – температура плавления кристалла, которая равна температуре кристаллизации T s , если пренебречь явлением гистерезиса в области плавления – кристаллизации. На основе данной схемы будем анализировать природу правила Симхи-Бойера (1).

Очевидно, что объем жидкости выше температуры плавления T f один и тот же, независимо от того, получена ли жидкость путем плавления кристалла или размягчения стекла (для данного вещества). Поэтому началом совмещения значений объема должна служить точка А при T f . Из нее по разным путям расходятся кривые V(T) для стекла (ACD) и кристалла (ABEE 0 ), которые ниже T g становятся параллельными прямыми (CD и EE 0 ). В самом деле, известно, что КТР в стеклообразном и кристаллическом состояниях равны. Поэтому наклоны прямых CD и EE 0 одинаковы.

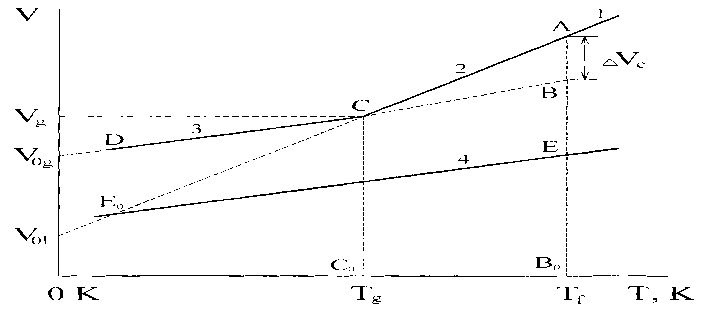
Рис. Температурная зависимость объема тела в жидком (1), переохлажденном (2), стеклообразном (3) и кристаллическом (4) состояниях. T g – температура стеклования, T f – температура плавления.

Из определения коэффициента объемного теплового расширения (КТР)

V V^A T )                                                        (2)

следует соотношение в А Т = A V/V, которое позволяет определить относительное изменение объема "жидкости" (если бы она, не стеклуясь, оставалась жидкостью до 0 К)

в l T g

Vg - V0-

V g

и стекла

V в gTg = -

—

g

V g

V 0 g

при их охлаждении от температуры стеклования до 0 К, т.е. в интервале температуры А Т = (T g - 0 К) = T g . Здесь V g = V(T g ) – объем при T g , V 0g и V 0l – объемы стекла и жидкости при 0 К (рис.). Вычитая почленно из выражения (3) соотношение (4), имеем

Ар T_g = ⁽ V 0 g ^— V 0 - ) ^g

.

g

Таким образом, величина Aр T_g в правиле Симхи-Бойера (1) имеет смысл относительной разности объемов стекла и жидкости, экстраполированных к абсолютному нулю температуры 0 К (иначе, относительного изменения объемов стекла и "жидкости" в интервале T g – 0 К).

Из рис. видно, что переход жидкость–стекло можно реализовать в принципе двумя путями: обычным изобарическим AD и изотермическим AB. В том и другом случаях процесс стеклования сопро- вождается изменением удельного объема на одну и ту же величину AVc, которая определяется разностью объемов жидкости Vl (Tf) и стекла Vg (Tf)

AVc = Vi(Tf) - Vg(Tf), где Vg (Tf) находится экстраполяцией объема стекла к температуре Tf. Геометрической мерой этого объема Vg (Tf) служит отрезок BB0, а объема Vl (Tf) – отрезок AB0, для Vg= Vg (Tg) – отрезок CC0 (рис.).

Используя определение КТР (2) и процедуру, аналогичную (3)–(5), для интервала температуры

A T = (T_f - T g ), для относительного приращения объема жидкости в интервале от температуры T_g до T_f

получаем соотношение V = AP(Tf - Tg) V g                                                                 (6) Вводя обозначение f = A Vc c g после небольшого преобразования равенство (6) можно представить в виде

( T              1 fE = A в T .1 — f- - 1 1 cg I T g      )                                              (7)

Для отношения температуры стеклования к температуре плавления известно эмпирическое правило Кауцмана-Бимена [3, 4], которое иногда называют правилом "двух третей"

T g               2 --- » const « — T f                 3                                                     (8)

Из приведенных соображений следует, что величина f c в равенстве (7) является однозначной функцией двух эмпирических правил (1) и (8), откуда она должна быть постоянной величиной: f_c ~ const.

В самом деле, на основе известных экспериментальных данных нами установлено, что относительное изменение объема вещества в интервале от температуры стеклования до температуры плавления (T f – T g ) у веществ различного химического строения в первом приближении постоянно (см. табл.)

f, = A V c /V g « const « 0.03 + 0.04                                (9)

Таблица

Относительное изменение объема Δ V c /V в интервале от температур стеклования T g до плавления T f

Вещество	T g ,	T f ,	V l (T f )	V g (T f )	f c = A V c /V g
	К		см3/г
Глицерин	185	291	0.795	0.765	0.037
Натуральный каучук	198	281	1.000	0.970	0.030
Манноза	297	405	0.689	0.669	0.030
Глюкоза	301	419	0.690	0.670	0.030
Галактоза	303	438	0.696	0.672	0.036
Полистирол	353	508	1.020	0.990	0.030
Поликарбонат	413	493	0.895	0.865	0.033
Кварцевое стекло	1473	1983	28.000*	27.300*	0.025
Стекло Na 2 O-SiO 2 **	673	1173	44.000*	42.000*	0.045

* значения молярного объема, см³, ** содержание Na 2 O составляет 33.3 мол.%

Таким образом, в результате анализа правила Симхи-Бойера установлено новое эмпирическое правило – постоянство относительного изменения объема в интервале от температуры стеклования до температуры плавления у веществ различного химического строения.