О прямолинейном течении в упруговязкопластическом цилиндрическом слое в условиях одностороннего прилипания

Прямолинейные движения вязкопластических сред изучались ранее в [1–3]. Учет влияния упругих свойств среды на параметры подобных движений оказался возможным только в рамках теории больших деформаций. Именно так были получены первые решения некоторых модельных задач прямолинейного движения упруговязкопластических сред с последующей разгрузкой [4–7]. В данной работе с использованием модели больших упругопластических деформаций, предложенной в [8, 9], и подхода, подробно описанного в [4–7], приводится решение задачи прямолинейного движения упруговязкопластического материала между двумя цилиндрами. Один из цилиндров движется, в то время как второй жестко закреплен.

2.    Основные модельные соотношения

Согласно [8] кинематика среды в декартовой прямоугольной системе пространственных координат Эйлера x _i определяется зависимостями

d -e. + p . -e,e,. /2-е., p,. - p ,e,. +e ,p,e ., ij ij p ij ik kj ik p kj p ik kj ik p ks sj ,

De _ij pp    p

Dt °ij ° ij ( ( ° k   ° k ⁺ z k ) e kj ⁺ e ik ( ° kj ° kj ⁺ z kj ) )/ ,

Dp _ij Dt

ppp ij    pik  kj ik pkj ,

Dn _ij    dn _ij

—- = —- - r,n, . + nr,

Dt dt ik kj ik kj , du   d u,

Vi = —^L = —^L + Ui V, ¹ dt d t ¹' j ^j

u i , j

ij

d u _i d xj ’

r. = (v . -v..)/2 + z..(s ,,m Л. iji , jj , i      ijsk , sk .

В соотношениях (1) приняты обозначения: dij — компоненты тензора деформаций Альманси, ey - eikekj [I, py — его обратимые и необратимые составляющие; ui, у — компоненты векторов перемещений и скоростей точек среды; DDt — используемая объективная производная тензоров по времени, приведенная для произвольного тензора ny; °p (источник в уравнении переноса для тензора необратимых деформаций) — компоненты тензора скоростей пластических деформаций. Наличие нелинейной составляющей zij тензора вращений rij , которая приводится в [8, 9], связано с выполнением требования неизменности тензора пластических деформаций pij в процессах разгрузки.

Если считать материал несжимаемым и принять во внимание условие независимости плотности распределения свободной энергии от необратимых деформаций, получатся аналоги формулы Мурнагана [8]:

^{СТ У}=" Р ⁵   ^Ei. ^(б kj" ² d k^

при Р у = 0 ( i , j , k = 1,2,3),

W ст ij=- Р15 у+^(5 kj- ekj)   при Ру* 0, d eik

W = - 2 p J ₁ -p J ₂ + bJ² + ( b -p ) J 1 J ₂ -x J 13 + ...,

_r L k при ^k I k при

Р у = 0,

Р у * 0,

• ^L 1    ^d kk ,    ^L 2    d ik d kj ,    1 1    e kk    e st e ts I"² ,   ¹ 2    e st e ts    e sk e kt e ts ⁺ e sk e kt e tn e ns /^4.

Здесь G _iy — компоненты тензора напряжений Эйлера-Коши; р , Р 1 — добавочные гидростатические давления; W = W ( е _у ) — упругий потенциал; p , b , x — постоянные материала; 5 _ky — символ Кронекера. Следует отметить еще раз, что напряжения (2) определяются только обратимыми деформациями.

В качестве пластического потенциала может быть использовано условие текучести

Треска

max |аi -сту | = 2k + 2р max |°pp |,

в котором ст _i , ° Р — главные значения тензоров напряжений и скоростей пластических деформаций; k — предел текучести; р — коэффициент вязкости.

Скорости необратимых деформаций связываются с напряжениями ассоциированным законом пластического течения

° Р =X"5F7, F1 (сту °Р ) = k, Х> 0.

3.    Начальное упругое равновесие и вязкопластическое течение

Пусть несжимаемый упругопластический материал, деформационные свойства которого соответствуют описанной выше модели, находится между двумя жесткими коаксиальными цилиндрическими поверхностями r = r ₀ и r = R , ( R >  r ₀). Начальное напряженно-деформированное состояние в материале такого цилиндрического слоя свяжем с усилиями на его граничных поверхностях. Под действием таких краевых усилий до момента начала пластического течения слой находится в состоянии упругого равновесия. Далее обсудим все возможные ситуации в задании граничных условий для последующего процесса упругопластического течения.

Рассмотрим случай, когда начальное упругое равновесие задается соотношениями

• u\ r - r ₀ = 0, ^ОД - r ₀ = a 0 , u l r - R = u 0 , О rrr = R =O ₀.                                            ⁽⁵⁾

Здесь и = u_z ( r ) — единственная не равная нулю компонента вектора перемещений, о _rr — радиальная компонента тензора напряжений. В дальнейшем будем использовать цилиндрическую систему координат r , ф , z .

Предельные значения и ₀ и о ₀ в (5) не могут задаваться заранее подобно а ₀, а должны рассчитываться из условий предельного упругого равновесия. Из формулы Мурнагана (2) следует, что отличие о ₀ от а ₀ определяется обратимыми деформациями в четвертой степени, поэтому впоследствии таким отличием пренебрегаем.

Полагаем, что среди состояний упругого равновесия имеется такое предельное состояние, когда воздействие на поверхности r = R приводит к срыву материала на границе r = r ₀. Иначе считаем, что на граничной поверхности r = r ₀ материал удерживается за счет сухого трения с коэффициентом трения покоя    f :

(|о _rz | - f |о _rr I)   <  0 при t <  0. Однако с момента времени t = 0 перемещение и ₀

^r = ^r 0

достигает такого предельного значения, что последнее неравенство обращается в равенство и материал начинает перемещаться вместе с поверхностью r = R как продеформированное упругое тело. В таком движении потребуем выполнения условий vr _ R =а t, (a- const), (|° rz| - f |° J + £ v )| = 0,                                     (6)

• ^{1 r} - ^r 0

где v - v _z ( r , t ) — компонента скорости перемещения, ^ — коэффициент вязкого трения. Наличие последнего связано с предположением о разрыве скорости на поверхности r - r ₀. Поскольку далее будет учитываться вязкость (с коэффициентом ц ) среды при ее пластическом течении, то естественнее было бы поставить условие прилипания. Но движение при срыве из состояния предельного равновесия подразумевает разрыв скорости, и это предопределяет выбор закона трения в форме второго соотношения из (6), тем более, что форма записи закона трения не влияет на корректность постановки задачи [6, 7]. Так как срыв из состояния равновесия происходит на поверхности r - r ₀, то на поверхности r - R остается условие жесткой спайки (см. первое выражение из (6)).

Рассчитаем параметры упругого равновесного состояния, соответствующего моменту начала пластического течения ( t - 0). Ненулевыми компонентами тензора Альманси в рассматриваемом случае являются : d _rr - - ( и ') ²/2, d _rz - и '/2, и' - д и /d r . Из зависимостей (2) для компонент напряжений в квадратичном приближении по и' , в рамках которого строятся решения в данной статье, получаем:

^О rr ^-О фф ^-- ( Р + ² И )^-( b + ц )( ^и ') ²/^{2 --} ^ ,     ^О zz ^-- ^ + ц ( ^и ')² ,     ^О rz ^- И ^и '.         ⁽⁷⁾

8g   8g   g - g

8g  8g„ g _ rZ । ZZ । fZ ^_ 0

8 r     8 z    r

Согласно уравнениям равновесия

---rr. +--- ^r z + r ----W = 0

dr    8z r переменная 5 является функцией только координаты z , так что 5 = gz - a0, где g — неизвестная постоянная. Для того, чтобы напряжения grr

G,„,„ и G были конечными фф ZZ

при z ^ да , необходимо положить g = 0. Тогда при граничных условиях (5) решение упругой задачи принимает вид:

^G rz = cl^r , ^G rr =^G фф = ^a о , ^G zz = ^a о ⁺ c 2/ ( h ^r 2 ) , u = ( cl h ) ^ln ( r/ r o ) .                   (8)

Для определения постоянной c воспользуемся условием пластичности (3), которое в рассматриваемом здесь случае принимает вид: g _rz|r = r = k . Отсюда c = kr₀. Так как a ₀ (задаваемое обжатие слоя) влияет только на распределение компонент нормальных напряжений, положим a ₀ = kJ f . В этом случае проскальзывание на внутренней поверхности начнется одновременно с пластическим течением на ней же при условии u о = ( ^kr o/н ) In ( Rr ) .

Компоненты обратимых деформаций, согласно первому уравнению (1), вычисляются по найденному полю перемещений из соотношений erz = drz = u 72 = kr0/(2H r) , err = - 3el /2, ezz = el /2.                                (9)

Развивающаяся с момента времени t = 0 область вязкопластического течения r ₀ <  r <  r 1 ( t ) ограничена поверхностями r = r₀ и r = r 1 ( t ) . В области r 1 ( t ) < r <  R материал по-прежнему деформируется обратимо, то есть r 1 ( t ) является движущейся границей области вязкопластического течения.

В области обратимого деформирования r ( t ) <  r <  R для компонент напряжений, аналогично (8), получаем

^G rz = c 1/ r , ^G rr = ^G фф = a 0 , ^G zz = a 0 ⁺ c l ²/ ( h ^{r 2} ) . (10) С учетом непрерывности компонент упругих деформаций на упругопластической границе r = r 1 ( t ) две последние кинематические зависимости из (9) будут справедливы и в области вязкопластического течения. Тогда, согласно формуле Мурнагана (2), для компонент напряжений с точностью до слагаемых второго порядка малости по e _rz в данной области имеют место выражения

^G rr = ^-( P l ^{+ 2} н )^{- 2} ( b + н ) el = ^{- 5} 1 ( t ) , ^G zz = ^{- 5} 1 ( t ) ⁺ 4 H el , ^G rz = 2 H e rz .

С другой стороны, интегрируя уравнения равновесия и используя условие непрерывности компонент напряжений на упругопластической границе r = r 1 ( t ) , можно показать, что в области вязкопластического течения r ₀ <  r <  r 1 ( t ) для компонент напряжений выполняются те же зависимости, что и в упругой области.

Пластический потенциал (3) в квадратичном приближении может быть записан в форме [10]:

F i (^g rz , ^ p ) = ^G 2 z ^- ( ^k + n^ pz ) 2 = 0.                                                          ⁽¹¹⁾

Следуя ассоциированному закону пластического течения (4), находим g _rz = k + pa rZ , ^ = £ P_z /( n ^£ ZZ + k ) . Сравнение этих соотношений и (10) позволяет определить скорость пластических деформаций

^£ pz = ( С 1 / r - k )/p .                                                                            ⁽¹²⁾

Учитывая, что на упругопластической границе r = r1 (t) sprz = 0, имеем: c1 = kr1. В области обратимого деформирования r1 (t) < r < R интегрирование уравнения равновесия приводит к выражению:

u = A(r) + at2/2, A(r) = (kr1 /ц)In(r/R)-(kr0/ц)In(r0/R), v = at.(13)

Кинематические зависимости drr = err + Prr — erz /2 - 2в„р„, dzz = ezz + pzz - e2 /2 - 2в„р„, d„ = e^ + p„, ddrL = ^ = vу 2, rr =- rrz = v'/ 2, s rz = v'/ 2 = s ez + s Pz = derz- + %,(14)

dt 5t                                                          5t5

pprr     pppzz     pppp rr dt       prz zr rz ,zz dt       prz rz rz ,rr zz rz rz , имеющие место в рамках квадратичного приближения, и краевое условие вязкого трения (6) позволяют найти скорости точек в области вязкопластического течения:

v = C ( ^r , ^r 0 ) + D , C ( ^r , ^r 0 ) = ( ² kJ n ) ( ^r i ln ( rr )^- r + г ) , D = k ( ^r i Л ^- 1 )Д .          ⁽¹⁵⁾

Принимая во внимание (15), а также равенство и' = 2 ( e _rz + p _rz ) и непрерывность перемещений на упругопластической границе r = r 1 ( t ) , для компонент перемещений в области вязкопластического течения находим и = A ( r ) + a t ²/ 2 + tC ( r , r 1 ) .

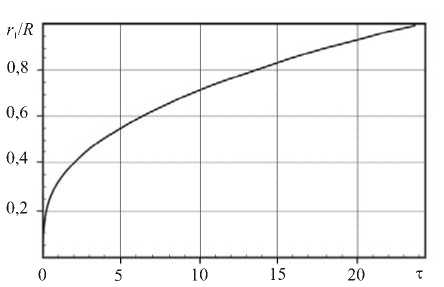
Рис. 1. Изменение радиуса упругопластической границы с течением времени при подвижной границе r = R

Из условия равенства скоростей (13) и (15) на упругопластической границе r = r1 (t) получаем уравнение для определения r1 , соответствующего скорости v = at на поверхности r = R :

C ( r 1 , r ₀ ) + D = a t .

На рисунке 1 показано изменение радиуса упругопластической границы r ₁ R от параметра т = a t ² / r ₀ при значениях r ₀ / R = 0,08, k / ц = 0,0005, ц _v r a /р = 100, ц r₀ /a Д = 500.

Пусть, начиная с момента времени t = t 1 , скорость движения внешней цилиндрической поверхности становится постоянной: v = a t 1 . Из уравнения (16) следует, что упругопластическая граница r = r 1 ( t 1 ) не изменяется и пластическая область дальше не развивается (пластические деформации растут только в пределах слоя r ₀ <  r <  r 1 ). Для последующего развития области вязкопластического течения можно увеличивать ст _rr : ст _rr = k ( 1 + у ( t - 1 1 ))/ f . Тогда скорость в пластической области и уравнение для определения r 1 ( t ) будут иметь следующий вид: v = C ( r , r ₀ ) + D - k y ( t - 1 1 )Д , C ( r 1 , r ₀ ) + D - k y ( t - 1 1 )/ ^ = a t 1 . Решение задачи в рассматриваемом случае, соответственно, для областей r 1 ( t ) <  r <  R и r ₀ <  r <  r 1 ( t ) записываем как и = A ( r ) + a t 1 1 -a t 12/ 2, v = a t 1 и и = A ( r ) + tC ( r , r 1 ) + a t 1 1 -a t 12/ 2.

4.    Торможение вязкопластического течения и разгрузка среды

Положим теперь, что с некоторого момента времени t = t2 > t1 внешний цилиндр начинает двигаться равнозамедленно со скоростью v = a t1 -Р( t -t2),                                                                           (17)

где в — заданная постоянная. Торможение продолжается до полной остановки внешней поверхности. Конечным моментом торможения является момент времени t_k = a t 1 /Р + t 2 . Начиная с момента времени t = 1 2 , при неизменном напряжении о rz = k' 1 /г , вязкопластическое течение будет продолжаться в области г₀ <  г <  г₂ ( t ) . В области г₂ ( t ) <  г <  г 1 не изменяются компоненты тензора необратимых деформаций, область г 1 <  г <  R является областью обратимого деформирования.

В области обратимого деформирования г 1 <  г <  R для компонент напряжений выполняются зависимости (10). Для компонент напряжений в областях г ₂( t ) <  г <  ' 1 и г ₀ <  г <  г ₂ ( t ) выполняются те же зависимости, что и для упругой области. Скорость пластических деформаций в области ^г 2 ( t ) <  ^г <  ^г 1 равна нулю и терпит разрыв первого рода на упругопластической границе г = г₂ ( t ) ; для нее выполняется соотношение (12). В области обратимого деформирования ' 1 <  г <  R после интегрирования уравнения равновесия получим: и = A ( г ) + F ( t ) , F ( t ) = a t 1 1 -a t 12/ 2 -Р ( t - t ₂ ) ²/2, v = a t 1 -Р ( t - t ₂ ) , где скорость точек среды в области вязкопластического течения г ₀ <  г <  г ₂ ( t ) удовлетворяет (15).

В области г ₂ ( t ) <  г <  г компоненты тензора необратимых деформаций изменяются в каждой точке слоя до того момента времени, пока поверхность г = г ₂ ( t ) не достигнет точки слоя; далее компоненты тензора сохраняют свои значения (то есть не зависят от времени, являясь только функцией координаты г ). Так как напряжение о _гz постоянно в процессе торможения, компонента перемещения в данной области, исходя из соотношения и' = 2 ( e _гz + p _гz ) , представляется в виде и = f ( г ) + g ( t ) . Учитывая, что в области обратимого деформирования скорость равна v = a t 1 - Р ( t - 1 ₂ ) , из условия непрерывности скорости на поверхности г = г₁ следует, что скорость будет такой же во всей области г ₂ ( t ) <  г <  г 1 . Тогда, согласно равенству скоростей на поверхности г = г ₂ ( t ) , имеем уравнение движения данной поверхности

C ( г ₂, г ₀ ) + D = a t 1 -Р ( t - 1 ₂ ) .                                                              (18)

На рисунке 2, а показано изменение радиуса упругопластической границы г ₂/ R от т .

Компонента тензора пластических деформаций p _гz в области г ₂ ( t ) <  г <  г₁ определяется из (12), (14) и (18) и представляется как p _гz = k ( t _k - D /Р )( ' 1 / г - 1 )/ц-- к ( г / г - 1 ) C ( г , г ₀ )/( пР ) . Используя это выражение, соотношения для напряжений (10) и учитывая непрерывность перемещений на границе r ₁ , находим перемещение в этой области:

и = A(') + F(t) + (tk -D/Р)C(',')-(C5 (',г-0)-C’ ('i,г>))/(2Р)•

В области вязкопластического течения г ₀ <  г <  г 1 ( t ) перемещение имеет вид: и = A ( г ) + F ( t ) + tC ( г , ' 2 ) + ( I k - D /Р ) C ( ' 2 , ' ) - ( C ² ( ' 2 , ' 0 ) - C ² ( ' , ' 0 ))/( 2 Р ) .

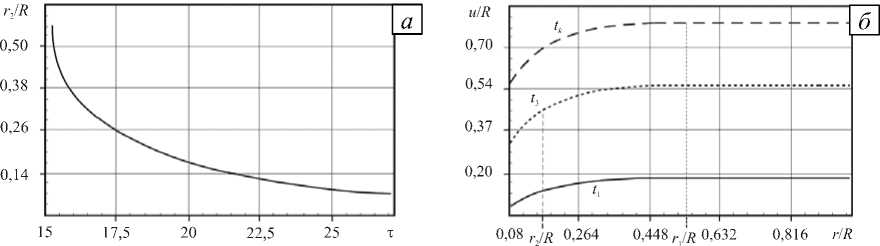
Рис. 2. Изменение радиуса упругопластической границы в процессе торможения ( а ) и перемещения точек среды в зависимости от радиуса в моменты времени t 1 , t 2 <  t 3 <  t * , t k ( б) при движущемся внешнем цилиндре и проскальзывании материала в окрестности внутренней поверхности

Согласно уравнению (18) в момент времени t * = t k - Dj в упругопластическая граница r₂ ( t ) дойдет до внутренней поверхности r₀ . С момента времени t = t * скорость становится одинаковой во всей области деформирования и вычисляется по формуле (17).

При дальнейшем уменьшении скорости внешнего цилиндра до полной его остановки напряжения, согласно (6), ведут себя по закону

о rz = с (t)/r, с (t ) = kr + £ r0 (ati-p( t - t 2 )) .                                           (19)

Перемещение определяется следующими зависимостями: u = A (r, t) + F (t) в области и      u = A (r, t) + F (t) + tC (r, r2) +

обратимого деформирования      r 1 <  r <  R

+ (tk - D! P) C ( r2, ri )-( C 2 ( r2, r ) - C 2 ( ri, r0 ))/( 2P) в области с накопленными необратимыми деформациями   r0 < r < r1;   при этом   A1 (r,t) = (c(t)/ц)In(r/R)-(kr0/ц)In(r0/R).

В конечный момент торможения функция c(t) и скорость, соответственно, равняются c (tk ) = kr0 и v = 0. На рисунке 2, б показаны перемещения точек среды в зависимости от радиуса в моменты времени t1, 12 < t3 < t , tk .

Уменьшение компонент напряжений до нуля приводит к разгрузке слоя. В конечный момент разгрузки, когда c ( t ) = о _rr = 0, как следует из соотношения (7), остаточные напряжения равняются нулю во всей области деформирования.

5.    Деформирование среды при движении внешнего цилиндрас возможным проскальзыванием материала в его окрестности

Рассмотрим случай, когда на поверхности движущегося цилиндра выполняется второе условие из (6): (| о _rz | - f |о _rr | + ^ [ v ])| ^ = 0; на поверхности внутреннего цилиндра зададим условие прилипания: u = v = 0. Теперь решение упругой задачи ^r = ^r 0         ^r = ^r 0

определяется через соотношения (8), где a ₀ = kr ₀ /( fR ) . Задание о _rz = а ₀ означает, что скольжение вблизи поверхности движущегося цилиндра начнется одновременно с пластическим течением на другой поверхности.

Итак, в момент 10 = 0 на внутренней поверхности начинается вязкопластическое течение. Как и в предыдущей задаче, упругопластическая граница r = r1 (t) разделяет область обратимого деформирования r1 (t) < r < R и область вязкопластического течения r0 < r < r1 (t). Найдем перемещения и скорости точек слоя в области обратимых деформаций u = A 2 ( r) + tC ( r1, Г0 ) , v = C (r1, r0 ) , A 2 ( r )=( kr1 /^) ln ( 4r0 ) (20) и в области вязкопластического течения u = A2 (r) + tC (r, r0), v = C (r, r0). Уравнение для радиуса упругопластической границы следует из второго условия (6), где v+ = at — скорость внешнего цилиндра, v- — скорость среды в окрестности внешнего цилиндра (второе уравнение (20)):

• -    C ( r i , Г о ) + a t = D 1 , D = k ( r /R - r , / R )Д . (21) При движении цилиндра с постоянной скоростью v = a t 1 граница r = r 1 ( t ) не изменяется, решение задачи имеет тот же самый вид. Чтобы вязкопластическое течение развивалось со временем, необходимо увеличивать ст _rr , как и в предыдущем случае.

В момент времени t = 12 > t1 начинается торможение внешнего цилиндра. С этого момента вязкопластическое течение будет

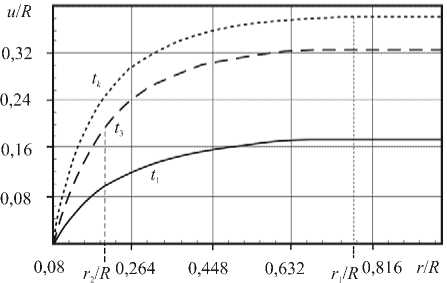
Рис. 3. Перемещения в зависимости от радиуса в разные моменты времени при движении внешнего цилиндра с проскальзыванием материала в его окрестности

продолжаться в области r ₀ <  r <  r ₂ ( t ) . В области r ₂ ( t ) <  r <  r 1 не изменяются компоненты тензора необратимых деформаций, область r 1 <  r <  R является областью обратимого деформирования. В области вязкопластических деформаций решение вычисляется по формулам (20). Упругопластическая граница r = r ₂ ( t ) удовлетворяет уравнению

• -    C ( r 2 , r , ) + a t i -P ( t - 1 2 ) = D i .    (22)

В упругой области и в области с необратимыми    деформациями, соответственно, решение задачи записывается в следующей форме:

u = A2 ( r ) + tC ( r2, r0 ) + ( tk - D1 /Р) C ( ri, r2 )-( C 2 ( ri, r0 )-C2 ( r2, r0 ))/( 2е) , v = C ( r2, r0 ) , u = A2 ( r ) + tC ( r2, r0 ) + ( tk - D1 /Р) C ( r, Г2 )-( C2 ( r, r0 )-C2 ( r2, r0 ))/( 23) , v = C ( r2, r0 )

и справедливо до момента времени t* = t _k - D 1 /р, когда упругопластическая граница доходит до внутренней поверхности r ₀ . В этот момент начинается разгрузка среды. Напряжению ст _rz отвечает первое соотношение из (19), где

| c (t )| = kr0 +^R (a t1 -p( t - t 2)).                                                           (23)

В области обратимых деформаций и в области накопленных пластических деформаций соответственно найдем

u = (c (t)/^) ln (r/ro) + (tk - D1 /Р) C (r1, ro)- C2 (r1, ro)/(2P),

u = (c (t)/^) ln (r/ro) + (tk - D1 /Р) C(r, ro)- C2 (r, ro)/(2P).

На рисунке 3 показаны перемещения точек среды в зависимости от радиуса в моменты времени t1, t2 < 13 < t*, tk при движении внешней цилиндрической поверхности, когда в ее окрестности может происходить проскальзывание материала.

6.    Деформирование среды при движении внутренней поверхности

Рассмотрим случай, когда условие (6) представляется в форме v|   = at, r=ro

(a = const), (|arz|-f |arr| 4v)| = 0, то есть на внешнем цилиндре задано условие вязкого трения, а внутренний жесткий цилиндр движется. Пока справедливо неравенство arz\r=R < f |arr|, считаем, что на внешней поверхности выполняется условие прилипания u\=R = vr=R = 0 . Решение упругой задачи имеет вид arz = cr , arr =афф= a0 = |c|/( fR ) , azz = a0 + c7(pr2 ) , u =( clP) ln ( r/R) .      (24)

При c = - kr₀ на поверхности r = r ₀ выполнится условие пластичности (11).

В момент времени t ₀ на границе r ₀ начнется вязкопластическое течение. В области обратимого деформирования решение задачи представляется в форме: u = A 3 ( r ) - tC ( r , r ₀ ) +a t ²/2, v =- C ( r_i,r₀ ) +a t , где A 3 ( r ) = - ( kr_i /p ) ln ( r/r ₀ ) - ( kr₀ /ц ) ln ( r ₀/ R ) . В области вязкопластического течения перемещение и скорость выражаются соотношениями: u = A 3 ( r ) - tC ( r , r ₀ ) + a t ²/2, v = - C ( r , r ₀ ) + a t . Уравнение для радиуса r = r_i ( t ) записывается как (21).

Если, начиная с момента времени t = t_i, скорость движения внутренней поверхности становится постоянной v = a t 1 , то в этом случае для областей r_i ( t ) <  r <  R и r ₀ <  r <  r_i ( t ) , соответственно, получаем: u = A 3 ( r ) - tC ( r , r ₀ ) + a t_it -a t ²/², v = C ( r , r ₀ ) + a t _i; u = A 3 ( r ) - tC ( r , r ₀ ) +a t_it -a t ²/² , v = - C ( r , r ₀ ) + a t 1 ; вязкопластическая область перестает развиваться, и, как уже отмечалось, чтобы заставить ее расти, нужно увеличивать a _rr .

С момента времени t = 1 ₂ начинается торможение внутреннего цилиндра. Его скорость определяется выражением (17). Решение задачи имеет вид:

• -    в области r_i <  r <  R

u = A3 ( r ) + F ( t )-tC ( r2, r0 )-( tk - D1 /Р) C ( ri, r2 ) + ( C 2 ( ri, r0 )-C2 ( r2, r0 ))/( 2P) ,

v = - C ( Г 2 , Г 0 ) + a t i -p ( t - 1 2 ) ;

• -    в области r ₂ ( t ) <  r <  r 1

u = A3 ( r ) + F ( t )-tC ( r2, r0 )-( tk - Di/Р) C ( r, r2 ) + ( C2 ( r, r0 )-C 2 ( r2, r0 ))/( 2p) ,

v = - C ( Г 2 , Г 0 ) + a t i -p ( t - 1 2 ) ;

• -    в области r ₀ <  r <  r ₂ ( t )

u = A 3 ( r ) + F ( t ) - tC ( r , Г 0 ) ,      v = - C ( r , Г 0 ) + a t i -p ( t - 1 2 ) .

Здесь радиус r = r ₂ ( t ) определяем из соотношения (22).

Данное решение справедливо до момента времени t = t * ( t* = t _k - D _i/р), когда упругопластическая граница доходит до внутреннего цилиндра радиуса r = r ₀. После этого начинается разгрузка. Напряжение a _rz находим по первой формуле (i9), а c ( t ) — по формуле (23). Скорость движения среды везде одинаковая и имеет вид (17). Таким образом, для перемещений среды в области обратимых деформаций и в области необратимых деформаций при торможении внутренней поверхности, соответственно, получаем выражения:

u = (-|C ( t )|A) ln ( rlro )-( kro N ln ( ro IR ) + F ( t )-( tk - D1 /Р) C ( r1, ro ) + C2 ( r1, ro )/( 4в) , u = (-|C ( t )|A) ln ( rlr0 )-( kr0 N ln ( r0 IR ) + F ( t )-( tk - D1 /Р) C ( r’ r0 ) + C 2 ( r, r0 )/( 4в) .

На рисунке 4, а показаны перемещения точек среды при движении внутреннего цилиндра с проскальзыванием материала в окрестности внешнего цилиндра в зависимости от радиуса в моменты времени t₁, t ₂ <  t 3 <  t * , t k .

В последнем из рассматриваемых случаев (6) принимает форму v r _ r = a t , ( a = const ) , ( a _rz | - f |a _rr | + £ [ v ])| = 0, а на внешней поверхности выполняется условие прилипания u| r _ R = v r _ R = 0. Решение упругой задачи имеет вид (24), только a 0 = k/ f , как в случае, описанном в разделе 3. В момент времени t = 1 0 на внутренней поверхности выполнится условие пластичности и начнется вязкопластическое течение.

Решение задачи в области обратимого деформирования r1 (t) < r < R записывается как и = A4 (r), v = 0, A4 (r) = (-kr/p) In (r/R), (25) в области вязкопластического течения ro < r < r (t)

и _ A 4 ( r ) - tC ( r , r ) , v _- C ( r , r ) . (26) Уравнение для радиуса упругопластической границы r _ r₁ ( t ) находим из второго условия (6), где v ⁺ = a t — скорость внутреннего цилиндра, v ^- — скорость среды в окрестности внутреннего цилиндра (второе уравнение (26)); оно имеет вид (16), как и в первом случае, когда движется внешняя цилиндрическая поверхность, а на внутренней возможно проскальзывание материала. Если с момента времени t _ t ₁ скорость движения поверхности становится постоянной, то решение определяется по формулам (25), (26), где r₁ _ const.

При уменьшении скорости внутреннего цилиндра в области r₁ <  r <  R решение принимает вид (25), в области с накопленными необратимыми пластическими деформациями r ₂ ( t ) <  r <  r₁ и в области пластического течения r _o <  r <  r ₂ ( t ) , соответственно:

u ^_ A 4 ( r )^-( t k ^- DI P ) C ( ^r , ^r 1 ) + ( C ²( ^r , r o )^- C ²( r b r o ) )/ ( 2 3 ) , v ^{_ o} ;

u ^_ A 4 ( ^r ) - ^tC ( ^r , ^r 2 ) - ( t k - DI P ) C ( ^r 2 , ^r 1 ) ⁺ ( C ² ( r 2 , r o ) - C ² ( ^r 1 , r o ) )/ ( 2 P ) , v" ^_ - C ( ^r , ^r 2 ) •

Уравнение движения упругопластической границы r _ r ₂( t ) представляется как (18). В момент времени t = t * ( t* = t _k - D /в ) эта граница достигнет внутреннего цилиндра и начнется разгрузка. Напряжение a _rz определяется по формуле (19), а для перемещений в области r ₁ <  r <  R и в области с накопленными пластическими деформациями соответственно получаем: и = ( - c ( t )/ ц ) ln ( r/R ) , и _ ( - c ( t )/ p ) In ( r/R ) - ( t _k - D /p) C ( r , r ₁ ) - C ² ( r_vr _o )/( 2 p ) . В конечный момент торможения | c ( t )| _ kr _o, а при полной разгрузке c ( t ) = o, a _rr = o.

На рисунке 4, б показаны перемещения точек среды в зависимости от радиуса при движущейся внутренней поверхности, в окрестности которой материал может проскальзывать, в то время как на внешней поверхности выполняется условие прилипания, в моменты времени t ₁, t ₁ <  1 2 <  1 ₂, t_k .

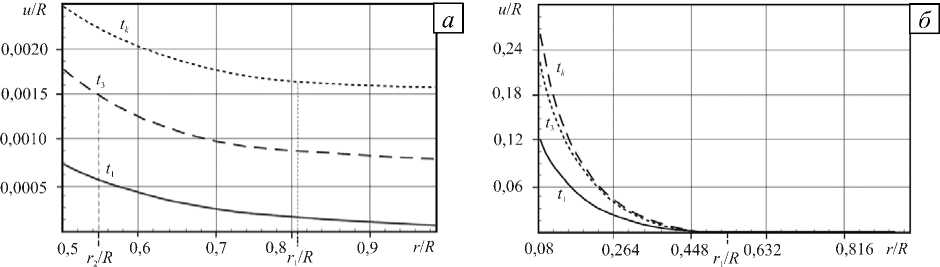
Рис. 4. Перемещения точек среды в зависимости от радиуса при проскальзывании материала в окрестности внешнего ( а ) и внутреннего ( б ) цилиндров при движущейся внутренней цилиндрической поверхности в разные моменты времени

7.    Заключение

В работе получены аналитические решения ряда краевых задач исследования прямолинейного движения упруговязкопластического материала в зазоре между двумя жесткими коаксиальными цилиндрическими поверхностями, когда на одной из поверхностей возможно проскальзывание материала. Решение получено в рамках теории больших деформаций. Рассмотрен простейший случай, когда обратимые деформации считаются малыми настолько, что при вычислении по ним напряжений можно пренебречь членами, содержащими эти величины в третьей степени. Необходимо заметить, что применяемая модель больших деформаций позволяет оставить в решении слагаемые более высокого порядка малости, а используемое приближение дает возможность получить аналитические зависимости для перемещений как в областях обратимого деформирования, так и в областях течения. Полученное решение моделирует процесс волочения для широкого класса конструкционных материалов с малыми, по сравнению с пластическими, упругими деформациями.

При построении графиков использованы значения постоянных величин для алюминия.