Принципиальное значение для нахождения решений уравнений физических полей имеет выбор анзаца - общей конфигурации полевых потенциалов, устанавливаемой из теоретико-групповых соображений (анзац Виттена, процедура Форгача-Мантона построения анзацев янг-миллсовских и хиггсовских полей для широкого класса пространственно-временных симметрий и др.). Симметрии используются также для построения законов сохранения, составляющих основу любой физической теории. Согласно теореме Э. Нётер и исследованиям группы американских ученых проективные и аффинные движения приводят к фундаментальным механическим и полевым законам сохранения. Главная трудность при построении таких законов сохранения заключается, по мнению авторов, в нахождении указанных движений

Векторное поле X на многообразии М с проективиой структурой П называется инфинитезимальным проективным преобраз о ванием^ или проективным движением (п.д.), если порождаемая этим полем в окрестности каждой точки р е М локальная 1-параметрическая группа состоит из (локальных) проективных преобразований, т.е. автоморфизмов проективной структуры. Для этого необходимо и достаточно выполнение следующих условий:

Zxg = %                              ⑴

(обобщенное уравнение Киллинга) и

• ▽从 У, Z, W ) = 2g(K Z )W^ + g(K W )Zg + g(Z, W »屮               ⑵

(уравнение Эйзенхарта)^ где У, Z, W е ТМ, (п + 1)g = divX. Если g = const, т. e. divX = const 、 то проективное движение является а ( 1 )( 1 ) ііішым. в частности, при % = cg гомотетическим (преобразование подобия), а при % = 0 изометрическим (сохраияющим метрику g).

Данная статья посвящена проблеме определения псевдоримаиовх многообразий (М, g), допускающих алгебры Ли инфинитезимальных проективных (в частности, аффинных) преобразований, более широкие, чем алгебры Ли инфинитезимальных гомотетий. Подобная задача для п-мерных собственно римановых и лоренцевых пространств была решена в работах Т. Леви-Чивита, А. С. Солодовникова, А. 3. Петрова и А. В. Аминовой ( [4], см. обзор в [9]). Для псевдоримановых многообразий произвольных сигнатуры и размерности проблема их классификации по алгебрам и группам Ли проективных преобразований, поставленная более ста лет назад, остается открытой.

Классификация пространств, допускающих негомотетические проективные движения, основана на разбиении их по типам в соответствии с алгебраической структурой производной Ли Lx g метрики g в направлении проективного движения X. определяемой в ка.ждой точке р е V С М характеристикой Сегре х тензора % = Lxg. Тип тензора Lxg определяет тип проективного движения X ii тип метрики g в области V. Такие метрики будем па ： зывать %- метриками типа х, а соответствующие пространства — %-пространствами типа %.

В работах [10] и [11] исследованы пятимерные %-простраиства типов соответственно {221} ii {32}. В данной работе с помошьто метода косоиормалыюго репера ( [9]. см. также [11]. где приведены необходимые сведения, касающиеся определения и свойств косонормального репера) определяются пятимерные %-простраиства типа {41} (теорема 1) и устанавливаются необходимые и достаточные условия существования проективного движения типа {41} (теорема 2).

1.    Вычисление 1-формы связности.

Пусть (У^ = £ ^д/д") — косонормалыіый репер в области V С М, 9% — каноническая 1-форма, %                                         一 сопряженная с У%. В терминах локальной координат ной системы каноническая форма 9 = Өг Ei задается соотношением ( [9], с. 96)

,

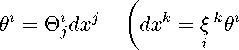
⑶ где (Ө]) - обратная матрица для

G) ：

I ^гө-= 琴

⑷

Пусть Ө һ — каноническая 1-форма, сопряженная с %, (У^) — (канонический) косонормалыіый репер в области V С М, в котором билинейные формы ди% имеют канонический вид

2                   2                                                    2

9ІҮ = £ 9р ，川 V = £ ( Лр + 2 屮)寿 + %о 三 а + 2gд, 2 屮 =£ 吊，

P=1           P=1                                   P=1

где 入 1 ,入 2 — не равные друг другу характернотические числа билинейной формы а = % — 2gg кратностей соответственно 4 и 1 (тип {41}),

91 = 6 1 ( Ө 1 Ө 4 + Ө2Ө3 + Ө з Ө2 + Ө4Ө1),  g2 = е2Ө₅Ө₅,

%о = ао = е1(Ө1Өз + Ө2Ө2 + Ө3Ө1)

⑸

,~          ~          ~          ~          ~       、

(1 = 4 , 2 = 3 , 3 = 2 , 4 = 1 , 5 = 5) , £ 1 ,^ 2 = ±1 .

Коэффициенты вращения Риччи 72Pz_e =— 加(左 определяются в области V С М равенствами ([8], § 30)

▽ %^У 三 ^2 ^ерУ2ре^Ур = Тр 匕 э,

P=1

где 7厶=ерМрк - компоненты 1-формы связности 叫 в косо репере (Уһ)： з；・=7；үӨ' = Q7,(/ = £еһе，7)"өһ.

⑹

һ=1

После ^замены % = а + 2gg уравнение Эігзенхарта (2) в косотюрма/ыюм репере (Уһ) примет

ВИД

匕口以 +〉: eh("hq7/“ + aph7%qr) = Gq^Yp屮 + GpfYq屮 h=1

(p,q,r = 1,..., 5). что равносильно

n

而pq +〉： eh(ahq〜刃 + "ph%R) = (Үдд)Өр + (Ypg)Oq ,                    ⑺ h=1

где ®pq = —^qp есть 1- ( ] ) орма’ свя ： зііостп.

Подставив в ⑺ вместо )pq и apq соответствующие канонические значения для типа {41}, получим

匕 g=Ү2g = узg = 0, "无 =2(У4g) 。 1, "赴 =2( 为 g)ө5,                 (8)

^ 13 = ：( Ү4д)Ө1 , ^ 14 =— (吗夕 ) 。 2 , ^ 15 = \ 丫⁵: Ө1 ,

2                                     入 2 — 入 1

^24 =^—( 吗 д^)Ө3,

^ 25

匕屮

(A2 — A1)2 Ө1 +

Ү5g

入 2 — 入 1

^Ө2 ,

Kg       Kg      Kg 夕

^34 = ^— (^Y4^g)^Ө4^, ^35 = 八---〕 Š& + 八---〕 І^Ө2 + ~\---]^Ө3,

( 入 2 — 入 1)³      ( 入 2 - 入 1)² 入 2 - 入 1

^ 45

Ү5g ( 入 2 - 人 1)⁴

Ө1 +

^Y5g    а ,     ^Y5g    а ,    ^Y5g   〃 , 吗屮 〃

( 》 2 — 人 1)^{3 Ө}2 + ( 。 2 — 人 1)^{2 Ө3 +} 》 2 — 人 1 ^Ө4 ⁺ 》 2 — 人 1 ^Ө5

Ипользуя （6）. найдем отстода коэ （ 1 ）（ 1 ） шпіепты вра ， ш,етшя Риччи ：

7314 = 二 -7134 =2е1 吗夕，7413 = -7143 = -е1 吗夕，7422 = -7242 : =-e1吗夕， 61匕8 e1为夕 7431 = 二-7341 — e1 人夕，7514 —  7154 - \    \，7523 — 入2 -入1 二 -7253 入2 —人1， e1为夕 e1为夕 7524 — 7254 = （д - д）2，7532 — --7352 入2 —人1， e1为夕 e1为夕 7533 —  7353 = （д    д）2，7534 —  7354 — （人2-人1）3， e1为夕 e1为夕 7541 — 7451 =人？ - 人]，7542 — 7452 — （人2-人1）2， £1%夕 £1%夕 7543 = 7453 =（人2 -Д1）3，7544 — --7454 一人2-人1， e2吗夕 7545 = 二 -7455 Д2 — Д1 Остальные коэффициенты 英/左 равны нулю. Из （8） следуют равенства 匕人1 = 2心4吗夕，匕人2 = 28*5为夕. ⑼ Используя полученные соотношения и формулу п 歐，匕］三▽“ 匕-▽у%м = £ е，（7，*% - 7lhk） 讦， /=1 составим скобки Ли векторных полей 匕，...，吗: ［匕，匕］= 0， ［匕，匕］=0， 明，吗］=-2（м夕）y2， ［匕，匕］= /9у Д2 - Д1 i， /，r]=0， ［K，W］ =-（吗同h， ［К，匕］= /8 一（人2-人1）2 1+ 必9 人2-人1"， 3 ［h，吗］—-2（吗同吗，                  （Ю） ［匕，匕］= /9 一（人2-人1）3 1+ '3 （人2-人1）2" + 》9 人2-人1m， m，匕］= /9 一（人2-人1）4 1+ '屮 （人2-д1）3%+ 》3              吗9 （人2-人1）2У3 1 Д2 - Д1 У4 1 Д2-人1Y5， остальные скобки Ли равны нулю.

Напомним, что система линейных дифференциальных уравнений в частных производных с неизвестной функцией и:

i         ~ ди         ,                              、

-"三Š （"，…選 ）我=0 （s = 1，…，?" = 1,---,n）, где £ * — компоііенты ? векторов косоиормалыюго репера （匕，...，厶），является вполне интегриру-s ем ой, т. е. допускает п - ? независимых решений и1，...，и「, если и только если все коммутаторы операторов системы （ [8], с. 143）

п

[匕，К]三匕匕-НК = £ е,（力st-方於）匕（s，t =1，...，？），              （11） т=1

где

皿% = &削 g ’ g^m 2 j "

—коэффициенты вращения Риччи, линейно выражаются через операторы системы К,..., 鬲( [7], с. 12).

Из приведенных выше формул следует, что системы дифференциальных уравнений

Yiu = У2& = 匕& = У5& = 0,

Hu = ^u = Y5U = 0,

Yi u = Y5U = 0, являются вполне интегрируемыми. Обозначим единственное решение первой системы и одно из двух независимых решений второй системы через u4, решение второй системы — через u3; решения третьей системы обозначим u2, а решения уравнения Y^u = 0 - через u1, u2, u3, u4. Система Y^u = Y2u = Y3u = Y4u = 0 также является вполне интегрируемой, ее единственное решение обозначим u5. В новых координатах т2 = u2, опустив штрихи, получим g2 = Q(t*2 , 1

Из (8) и (9) следует, что 尢 при этом

g2 = p(т*5, g3 = g4 = g5 = g4 = g5 = g5 = 0.

зависит только от т⁴, а 治- только от т⁵: 尢 三 /і(т⁴), А2 三 /2 ( т⁵)

屮 =2 ( 4 / 1 + / 2) .

2.    Основные уравнения.

Приравнивая в каждой координатной окрестности U координаты векторных полей в правых и левых частях уравнений (10), с учетом формулы

1 ° g¹dig¹ - g1dig1 — g²”¹ = 0,

2 。 g1dig² =0,

3 ° g¹ dig¹ - g1dig1 — g2d2g1 - g³d3g¹ = 0,

4 ° g1d1g² = 0,

5 ° g1d1g³ = 0,

6 ° g1d1g1 - g1d1 g¹ - g²d2g1 - g³d3g1 - g⁴d4g1 = - g⁴/1 g¹,

7 ° g1d1g² = - g⁴/ ’ g²,

8 ° g1d1g³ = 0,

11 ^。

12 。

13 。

14 。

21 ^。

22 ^。

23 ^。

24 ^。

9 。 ) 1д1)⁴ = 0, 14

100 )5д5)1

)1д1)5 = 0,

¹—¹- 产 f"¹. 2 /2 - /1 f ^/2) ,

)1д1)1 + )²д2)1 - )1д1)1 - )²д2)1 - )³дз)1 = 0,

)1д1)² + )²д2)² - )1д1)² - )²д2)² - )³дз)² = 0,

)1д1)3 + )2д2)3 = 0,

150 产&产 +1д2 产一产&产一 1д2 产一 1& 产一 9 为产 = - 2)4/1 产,

24 24 42 42 42 42

16 。 e1di ) ² + ) ²d2 ) ² - ) 1ді ) ² - ) ² 汲 ² - ) ³дз ) ² Т⁴%)² = - 2)4/1 ) ²,

)5д5)2

19 。

24 42 42 42 42

17^o )1 д1 )³ + )2д2)³ = - 2)4/1 )³,

24 24

18o )1 д1 )4 + )2д2)4 = 0, )1д1)5 + )2д2)5 = 0,

)5д5)1

1     1

2 /2 - /1

¹ ——¹——)5 f‘ )1 - ¹ —¹— )5 f‘ )1. 2 (/2 - /1 ) ²5 ^/2)     2 /2 - /11 ^/22 ,

)5/2)2,

)1ді)1 + )²д2 ) 1 + )3 дз)¹ - ) 1ді ) 1 - ) ²д2 ) 1 - )³дз )1 - ) 4д4 ) 1 = - 3 ) ⁴/1 )1,

34 34 34 43 43 43 43

)1ді)² + )²д2)² + )3 дз)² - )1ді)² - )²д2)² - )³дз)² - )4д4)² = - 3)4/1 )²,

34 34 34 43 43 43 43

)1д1)³ + )²д2)³ + )3 дз)³ - )1д1)³ - )²д2)³ - )³дз )3 - )4д4)³ = - 3)4/1 )3,

25 ^。

4 34 34 43 43 43 43

)1д1)⁴ + )² д2)⁴ + )³дз)⁴ = - 3/1 ()⁴)²,

34 34 34

26 ^。

)5д5)1

1     1

2 /2 - /1

27O

)5д5)2

£⁵ У‘ 产— ¹——¹—— £⁵ /‘ 产— ¹——¹— 5 ^/2)    2(/2-/1 ) ²І ^/2)    2 (/2-/1 )

1—1— )5/‘)2 - 1----1——)5/К)2.

2/2-/1"'2f    2 (/2 - /1)2І /22 ,

28O

)5д5)3

¹—¹— 产 f"³. 办 f f J J 2J ，

² /2 ^- /15   3

29 ^。

)1д1)5 + )2д2)5 + )3 дз)5 = 0,

)5д5)1

¹—¹- 破 f"¹ 一 ¹——¹—— 破 f"¹ 一 2 /2 - /1 ”^2f    2 (/2 - /1 ) ²5 ^/2)

2 (/2 - /1 )3

)5 /‘ )1 - 1-----1-----)5 /‘ )1

)f 2^f           / 、 4⁾/2^),

5   2    ^{2 (/}2 - 力 ) 5    1

■3)5/2)1,

31° 1д5І

¹____¹____С⁵ f ‘ С²

2 /2 - /1 f 咲

¹¹ A⁵ f"² — ¹¹ A⁵ f"²-2 (/2 - /і)^{2f /2f} 2( / 2 - / i )^{3 f /2}2 ,

32° f5d5f3

¹¹ ， ⁵ f‘ ， ^{3 2}/2 - /1 ^{f /2f}

¹¹ A⁵ f"³-2 (/2 - /1)^{2 f /2}3 ,

33° f5@5f4

2 ■ f5/2 f4

34° f1 dif5 + f2%f5 + f3d3f5 + f4d4f5 = /—/f4/1 f5

(штрих означает производную функции по ее аргументу, например, /‘ 三 d/i/dx⁴).

Интегрируя уравнения 10°, 2°, 20°, 5°, 14°, 27°, 11°, 19°, 29° и 34°, найдем f1

(/2 - /О¹/^{2 Т}1^(Х1

,x2, x3, x4), f2 2

(/2 - /1)^{1/2 T}2^(x2

,x3,x4),

^f3 = (/2 - /1 ) ^1/2T3 ( ^x3^{,x4), f}5 = (/1 - /2)^2T5^(x5)-

После преобразования координат

x

/ T-1dx1

x2‘ = / T-1dx2,

x3’ = / T-1dx3,

′

x

x4, x5’ = / T5-1dx5,

не меняющего полученных ранее результатов, опустив штрихи, имеем

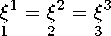
(/2 - /1 ) ^1/2 ,

^f5 =(/1 - /2 ) ² .

Интегрируя уравнения 9°, 18°, 25° и 33°, найдем

4     3(/2 - /1 )^1/2(/1 (x³)+ 3(x4))

Возможны два случая: /1 = 0 и /1 = 0. В первом случае сделаем замену координат x4

/1(x4), x* =x* (р = 4) и положим 3 = (/1)-1з, тогда

£ = 3(/2 - /1)^1/2(x³ + 3) , ^fP = ^fР 位 =⁴⁾

Во втором случае сделаем замену x4 = 3 J 3dx4. Опустив черту, объединим оба случая формулами

/1 = £1x4 + (1 - £])С1 © = COIlSt), f4 =(方 - /1)1/2.   (А 三 3£1 (x3 + 3(x4)) + 1 - £1), где £1 равно () пли 1.

Интегрирование уравнений 1° и 20° дает следующий результат:

^f1 = 2(/2 - /1)1/2 ⁽E1 ^{+ D(x2,x}3^,x4 )) , где введено обобзначение

£1 三 72-71 ，

Выполнив замену координат x1’ = x1 - I / Odx2, xp‘ = xp (р = 1), опустив штрихи, получим

І1 = 2(/2 -力) 1 / 2 *1 ・

Интегрирование уравнений 3°, 12° и 26° дает

€ 1 = I— — + (Е 。 ² + 2& ， ³ ,， ⁴)) ,

3     8^(/2 ^-/1 ) ^1/2

где =...1...

• ² — (/2-/l)²

В новых координатах

• т¹ ’ = 戸 —I / /dr³, 逆‘ =£p ( 召 =1), опустив штрихи, имеем

• ^€1 = 8(/2 - /1 )^{1/2 ((Е}1⁾² + ²*² ) .

Интегрирование уравнений 4°, 13° и 27° дает

• ^€2 = 2(/2 -1/і)1 / 2 ^(Е1 + ^{Ғ (}Ю

Сделаем замену координат

• *' = *^-/ ® м = "S=²⁾,

будем иметь

• ^€2 = 2(/2 - /і)^{1/2 Е}1.

В результате интегрирования уравнений 8°, 17°, 24° и 32° получим

• ^€3 = 2—(/2 - /1)1 / 2 ( '*1 + ³P⁽") ^-我 ¹"² ) •

После замены координат

• т³ ’ = т³ — / Pdr⁴, т^р ’ = т 「 (召 =3) в новых координатах, опустив штрихи, будем иметь

• 4³ = 2—(/2 - /і)^1/2 ( '*1 ^- 我 ¹" ) .

Интегрируя уравнения 7°, 16°, 23° и 31°, найдем

€² =         ¹ f 、 1/2 ( 2'*2 + '(*1)² + 3Q(r⁴) - 8еіт1 ) .

4    ⁸ '(力^{一 /}1 ) ^1/2

Выполнив замену координат

• ^т2‘ ”^2-/ Q"”⁴' м =丿= ²⁾, получим

• ^€2 = 8 ' ( / 2 - / і)1/2 ( ² ' *² + ' ^{(Еі)2 -} 涎 ¹" ).

Интегрируя уравнения 6°, 15°, 22° и 30°, будем иметь

• ^€1 = 6( / 2 -¹ / l)1/2 (*3 + 4*1*2 + |^(Еі)3) , где

ез = ...1...

• ^{3 —} (/2 - /і)3

  
  
3.    һ-пространства типа {41}.

Используя найденные значения компонент векторов косонормального репера

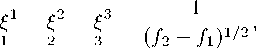
2     2(-2 -力 )3 / 2 , 3     8(/2 - /і)5 / 2 ,

• ²                        £1

• ²     2(/2 - /і)^3/2 ' ²     16(/2 - /і)^7/2 ,

• ²2 = 8(/2 - /і)^1/2 ( (/2 - /і)² - 12)'

  £ ³ =------¹

  ²     2(/2 - /і)^1/2

  
  

  К-л - ； '

  
  

• ² — 4/ 2 - / і )^{1 / 2} ' ² — (/1 - /2 ) ² '

А = 3^1 ( т ³ + ® (т⁴)) + 1 - £і' по (формулам (3). (4) вычислим компоненты каііоішческпх 1- ( ] ) орм в натуральном репере

。 1 = ( / 2 - / і )^{1 / 2} А/т ⁴ '

報 =(/2 - /і)^1/2 0т ³ - (2 / - / - 2fiT²) 4т⁴) '

“3= ^{( /}2^{-/і ) 1/2} 0^{T2 -} 2 к-л^- Gu2-W^{- е}1^т1+ ”/і ) 2' 。-^{( /}2 ^-/1 ^{) 1/2} 0^т1^- 2 与 ^-8ёйр -

/ 1 А        1 £]Т1     1   £iT²    、    4 、

16 (/2 - /і)3 ⁺ 2 「 1 + 4 (/2 - /і)^{2   T} '

“5 = (/1 - /2)— и затем по формулам (5) — компоііеиты метрики g и билинейной формы 九 в натуральном репере (Х〃). Подсчитав символы Кристоффеля найденной метрики g, непосредственной проверкой убедимся в том, что тензорные поля g’％ и g удовлетворяют уравнению Эйзеихарта. В итоге получим следующие результаты.

Теорема 1 Пусть М есть 5-мерное многообразие с метрикой g и связностью Леви- Чивита V. Пі/стъ 0-“орма 夕 и си.м.ме机р〃и〃〃/ билинейн(ія форма 九 х(ц)(штер'и х = {41} определены в М 〃瓜〃 а іье-копк >р< > й(> бааснш V С М и / z:t/ стъ /і' /2 — Р〃з ./ш “ іные характ ери с mu1 匕 еские корни билинейной формы 九一2gg кратностей соответственно / u」.Для того чтобы 九'g u g удовлетворяли уравнению Эйзенхарта, т. е. для того чтобы М было һ-пространством типа х = {41}, необходимо и достаточно, чтобы выполнялись равенства g = gi + g2'                                               (21)

^һ = ^(4/і + 力須 + ^/igi + ^/2g2 + ^һо,

(22) g = 2/1 + 2/2

и вокруг каждой точки р е V С М существовала каионическая карта (т, U ), в которой £i9ilu = 24/2 — fi)dx1dx⁴ + 2(/2 — fi)dx²dx³ + 2 ( 2£1 (力 — fi)x² — A ) dx2dx4- dr³2 + 2fi ( (/2 — /i)x1 — 2x² ) dx³dx⁴+

4^i ((/2 — /i)x1x² — x²2 — I Ax¹^ dx⁴2,

62921 u = (/1 — /2)4dx52, ei^o|u = 2A(/2 — /i)dx2dx4 + (/2 — /i)dx32 + 2(2£і(,/2 — /1)x2 — A) dx3dx4+

4fi

((/2 — /1) (x22 + ^Ax1) — Ax2) dx42, где /і = £避4 + (1 — £1)C1・ /2 = £2x5 + (1 — £2"2： q,C2 — con•品.A = 3印(x4 + ^(x5)) + 1 —印.印.功 принимают независимо значения 0 или」,61,62 = ±1, ® — функция x5.

Отсюда следует

Теорема 2 Векторное поле X е ТМ тогда и только тогда является (локальным) проективным движением типа {41} на 5-мерном псевдоримановом многообразии (М,д), когда выполняется равенство Lx 9 = 瓦 4е метрика 9 и билинейная форма 九 определены формулами (21)-(23) (теорема I).