О прогнозировании динамики показателей промышленного производства региона (на материалах Вологодской области)

Прогнозирование предстает значимой формой управления процессами социальноэкономического развития региона. В широком смысле прогноз – это предполагаемый сценарий развития некоторого процесса при возможных изменениях внешней среды. В настоящее время вопросы прогнозирования социально-экономического развития являются весьма актуальными, поскольку, согласно действующему законодательству, выступают основой для планирования бюджета региона на различные временные периоды. Кроме того, прогнозные индикаторы важны и для выявления направлений совершенствования системы стратегического планирования. Особое место в прогнозировании социально-экономического развития региона занимает промышленное производство. Промышленность – важнейшая отрасль экономики региона, обеспечивающая ведущую роль структурных преобразований экономики, внедрение достижений НТП, ускорение развития экономики региона и более полное удовлетворение потребностей общества (Ускова и др., 2013).

Исследование отечественного и зарубежного опыта в области прогнозирования показало, что степень обоснованности и точности полученных результатов во многом зависит от методик, используемых при получении прогнозных значений (Bom, Rachinger, 2019; Jadhav et al., 2017; Growiec, 2018; Liu, Papageorgiou, 2019; Mo et al., 2020; Motorin, 2015; Tomal, Ciborowski, 2020; Аитова, Орешников, 2017; Кашинцев, 2015; Клименко и др.,

2022; Лясковская, 2022; Носков, 2022; Носков, Бычков, 2022; Орешников, Аитова, 2019; Труфанова, Нещеменко, 2019; Халява, Еры-гин, 2022). В своих работах ученые применяют различный методический инструментарий, большей популярностью пользуются экономико-математические, нейросетевые и имитационные модели. Изучение работ по исследуемой теме выявило целесообразность применения моделей, сочетающих преимущества различных подходов. Таким образом, для выявления взаимосвязи между показателями и составления уравнения зависимости было принято решение воспользоваться методом регрессионного анализа, поскольку с его помощью можно легко оценить степень тесноты связи между показателями. Для прогнозирования независимых переменных в уравнении регрессии использован экстраполяционный метод как наиболее наглядный и доступный способ расчета прогнозных значений.

При этом исследователи приходят к различным выводам при анализе социальноэкономических систем в зависимости от масштаба изучаемых территорий. Так, на уровне страны воздействие инвестиций и течения времени на промышленное производство является несущественным, в то время как достаточно сильное влияние оказывает производительность труда (Рыбалкина, Тусков, 2018). На региональном уровне чаще исследуется взаимосвязь характеристик инвестиционной активности и ВРП (Трусова, 2013). На уровне муниципальных образований (в частности на примере г. Салават Респуб-

Вологодская область         Российская Федерация

Рис. 1. Индекс физического объема производства промышленной продукции, % к предыдущему году

Составлено по: данные Росстата.

лики Башкортостан) авторы отмечают, что ключевыми факторами развития являются бюджетные трансферты и динамика доходов населения (Орешников, Аитова, 2019).

Таким образом, целью нашего исследования стало прогнозирование показателей промышленного производства Вологодской области на долгосрочный период (до 2032 года). Следующий шаг состоит в определении дальнейших задач исследования: рассмотреть динамику ретроспективного и текущего развития промышленного производства региона; исследовать показатели, проявившие высокую степень согласованности в изменении признаков; разработать линейную модель множественной регрессии и произвести расчеты прогнозных значений.

Ретроспективный анализ промышленного производства

К ведущим отраслям промышленности Вологодской области относятся металлургия, химическая промышленность, деревообработка, производство готовых металлических изделий, машин и оборудования, пищевых продуктов, обеспечение электрической энергией, газом и паром1.

По данным Росстата, за 2021 год объем отгруженных товаров собственного произ- водства, выполненных работ и услуг собственными силами в промышленности составил 1295,6 млрд руб., что в сопоставимых ценах на 0,2% выше уровня предыдущего года. В структуре видов экономической деятельности выпуск предприятий обрабатывающей промышленности составил 96,2%, производства и распределения электроэнергии, газа и воды – 3,7%, добычи полезных ископаемых – 0,1%. В целом динамика индекса физического объема производства промышленных товаров в регионе схожа с общероссийской (рис. 1).

Резкое снижение индекса физического объема производства промышленной продукции отмечалось в 2009 году, основная причина – последствия финансово-экономического кризиса. В Вологодской области снижение темпов роста наблюдалось и в 2012–2013 гг. Указанный временной промежуток также пришелся на годы экономической нестабильности. При этом отмечено расхождение в динамике на региональном и страновом уровне в 2020–2021 гг., что во многом обусловлено различной структурой промышленности и снижением спроса на металлопрокат (вследствие охлаждения инвестиционных тенденций) на мировых рынках в период пандемии.

Моделирование показателей корреляционно- регрессионным методом

В ходе разработки регрессионной модели была использована классическая экономическая зависимость между объемом промышленного производства, инвестициями и трудовыми ресурсами (Марченко, Бурдакова, 2019). Для нейтрализации воздействия стоимостного, объемного, качественного и структурного факторов выполнен пересчет стоимостных показателей из фактических в сопоставимые цены (табл. 1).

Таблица 1. Исходные данные, в ценах 2021 года

Год	Объем промышленного производства, млн руб.	Инвестиции в основной капитал промышленных производств, млн руб.	Численность занятых в промышленности, тыс. чел.
	Y	X1	X2
2005	900	217	143,3
2006	964	175	138,1
2007	1012	176	136,6
2008	964	174	132,6
2009	872	135	117,2
2010	975	173	116,0
2011	1030	219	117,7
2012	1043	204	114,9
2013	1070	161	110,3
2014	1109	137	103,1
2015	1138	156	97,0
2016	1136	163	94,1
2017	1163	160	97,7
2018	1216	138	94,5
2019	1264	199	93,7
2020	1293	273	93,0
2021	1296	207	90,5
Источник: данные Росстата.

Объем промышленного производства – это зависимая переменная Y. Предположим, что на нее оказывают влияют независимые переменные Х1 – инвестиции в основной капитал и Х2 – численность занятых в экономике.

Для оценки тесноты связи между показателями применялся метод корреляционного анализа. Линейный коэффициент корреляции может принимать значения от -1 до +1, в зависимости от этого связь между признаками может быть слабой или сильной (тесной) (Яшин, Солдатова, 2015). Оценка этой зависимости производится в соответствии со шкалой Чеддока:

r xy < 0,1 – отсутствует;

0,1 < r xy < 0,3 – слабая;

0,3 < r xy < 0,5 – умеренная;

0,5 < r xy < 0,7 – заметная;

0,7 < r xy < 0,9 – высокая;

0,9 < r xy < 1 – весьма высокая.

При этом в качестве данных использована динамика индикаторов к уровню 2021 года, принятому в качестве 100%. Подобный подход успешно апробирован в работе В.А. Бессонова². В результате проведенного анализа получена матрица коэффициентов парной корреляции (рис. 2).

	Y	XI	X2
¥	I
XI	0,815237555	1
Х2	-0,857179608	-0,6431775	1

Рис. 2. Результат корреляционного анализа

Источник: составлено авторами.

Анализ первого столбца матрицы показал, что компоненты «Инвестиции в основной капитал промышленных производств» (0,8152) и «Численность занятых в промышленности» (-0,8571) по абсолютному значению проявляют высокую связь с зависимой переменной, вследствие чего в дальнейших расчетах они были включены в линейную модель множественной регрессии. Минусовое значение при коэффициенте Х2 означает обратную зависимость индикаторов.

Значимость полученных коэффициентов корреляции модели (между Y и X1, Y и X2) оценена с использованием t-статистики:

r YX1 √ n- 2  0,815√ 17 - 2

tрасч1 =            =               = 5,45

2       √1 - 0,815 ²

√1 - rYX1

r √ n - 2   0,857√ 17 - 2

t расч2 = ^YX2       =               = 6,44

2      √ 1 - (0,857) ²

√1 - rYX2

где:

r – выборочный коэффициент корреляции;

n – объем выборки.

Табличное значение критерия Стьюдента соответствует t табл = 2,1315. Сопоставив полученные величины индикаторов с табличными, можно сделать вывод о том, что соответствующие показатели коэффициентов корреляции являются значимыми (t табл > t табл ).

Результат проведенного регрессионного анализа переменных приведен на рис. 3.

Согласно протоколу анализа, уравнение зависимости объема промышленного производства от инвестиций в основной капитал промышленности и численности занятых в промышленности представлено ниже:

Y= 112,31 + 0,176 ∗ X1 - 0,295 ∗X2 (1)

Интерпретировать уравнение можно следующим образом:

– свободный член уравнения 112,31 показывает усредненную величину промышленного производства при Х1 = Х2 = 0;

– коэффициент переменной Х1 показывает, что увеличение инвестиций в основной капитал промышленных производств на 1% сопряжено с приростом выпуска промышленности на 0,176%, что может быть связано с высокой капиталоемкостью современного промышленного оборудования;

– коэффициент переменной Х2 показывает, что растущая в ходе модернизации производительность труда работников промышленных производств позволяет обходиться меньшей численностью производственного персонала (этот показатель снижается на 1% при росте промышленного производства на 0,295%).

Качество линейной модели множественной регрессии проверено с помощью ко-

Регрессионная статистика
Множественный R	0,923879629
R-квадрат	0,853553569
Нормированный R-к	0,83263265
Стандартная ошибка	4,1746262
Наблюдения	17
Дисперсионный анализ
	df	SS	MS	F
Регрессия	2	1422,051136	711,0255682	40,79904799
Остаток	14	243,9850547	17,42750391
Итого	16	1666,036191
		Стандартная	t-
	Коэффициенты	ошибка	статистика	Р-Значение
Y-пересечение	112,318	10,17802951	11,03534528	2,72117Е-08
Переменная X 1	0,176	0,052275591	3,369975835	0,004578343
Переменная X2	-0,295	0,069343497	-4,249991562	0,000808158

Рис. 3. Протокол регрессионного анализа

Источник: составлено авторами.

эффициента детерминации R2 (Кинякин, Милевская, 2014). Было определено, что переменными «Инвестиции в основной капитал промышленных предприятий» и «Численность занятых в промышленности» обусловлено 85,4% вариации индикатора «Объем промышленного производства», еще 14,7% объясняется влиянием прочих обстоятельств, не используемых в модели.

Значимость уравнения множественной регрессии оценена с использованием критерия Фишера. Расчетное значение F-критерия, как и коэффициента детерминации R², приведено в протоколе регрессионного анализа (значение равно 40,8). Уравнение регрессии можно считать значимым на уровне α , так как расчетное значение F > F табл. , где F табл. – табличное значение F-критерия Фишера, равное 3,68. Следовательно, допустимо использование данного уравнения для анализа и прогнозирования.

Для расчета прогнозных значений объема промышленного производства (Y) необходимо найти ожидаемые значения факторов инвестиций в основной капитал промышленных производств (X1) и численности занятых в промышленности (X2). Для расчета прогнозных значений показателей использовались экстраполяционные методы.

Для фактора Х1 «Инвестиции в основной капитал промышленных производств» в качестве аппроксимирующей функции определена следующая полиномиальная модель:

X1 = 0,4277x2 - 3,6218x + 31,07

График полученной модели временного ряда приведен на рис. 4 . Используя данную функцию, с вероятностью 75,4% (R² = 0,7537) можно утверждать, что к 2032 году ожидаемый объем инвестиций в основной капитал промышленных производств вырастет на 19,2% к уровню 2021 года (или на 99,1 млрд руб. в постоянных ценах). Спрогнозированные значения, основываясь на ретроспективных данных, демонстрируют стабильный рост показателя на протяжении всего исследуемого периода.

При этом на фоне санкционного давления, существенно затрудняющего поступление инвестиций и компонентов из внешних источников, остаются чрезвычайно актуальными вопросы выявления ресурсов для проведения мероприятий, имеющих целью построение современного индустриального базиса в российской экономике. В связи с этим нам видится безальтернативной концентрация внимания на внутренних факторах формирования собственного про-

x = 0,4277x2 - 3,6218x + 31,07

R2 = 0,7537

Рис. 4. Ожидаемый объем инвестиций в основной капитал промышленных производств Источник: составлено авторами.

мышленного капитала. Однако для их вовлечения в воспроизводственный процесс потребуются понятное для всех слоев населения направление развития отечественной экономики и соответствующая промышленная политика. Можно привести для сравнения опыт советской индустриализации, проводимой при более жестких условиях, но поддерживаемой осмысленной политической волей.

Другой важной задачей является конвертация сырьевого потенциала России в конкурентный. Ключевым приоритетом должно стать производство продукции более высоких переделов из первичного сырья (в случае Вологодской области речь идет о металлах, химических веществах, древесине).

Также стоит отметить сдерживающее влияние фискальной и монетарной государственной политики, во многом ориентирующейся на уровень инфляции и курс национальной валюты. Такой подход учитывает на «симптомы», являющиеся своего рода производной от реальных экономических процессов, и потому уместен для опоры бюджета на экспорт энергоресурсов, но создает определенные трудности для структурных преобразований экономики, ставящих целью организацию высокодоходных производств и увеличение производительности труда. При этом льготы определенным категориям предпринимателей не способны перекрыть тормозящее действие от завышения ставок на коммерческое кредитование, поскольку лишают производителей-льготников приемлемого объема внутреннего спроса, что отчасти подтверждается динамикой трудовых индикаторов промышленности, концентрирующейся по большей части на производстве и избегающей наращивания трат на НИОКР.

В то же время отметим, что со стороны органов власти предпринимаются усилия по повышению устойчивости экономики в «проблемных» аспектах. В частности, в последние годы нарастает интерес к вовлечению территорий во внутристрановые произ- водственные цепочки, о чем свидетельствует закрепление их значимости в качестве фактора развития внутреннего рынка в Сводной стратегии развития обрабатывающей промышленности Российской Федерации3 («В сфере потребительских товаров следует сосредоточиться на обеспечении платежеспособного спроса, как внутреннего, так и внешнего»). Установление в Стратегии в качестве общего принципа развития промышленности выхода на смежные стадии производственных цепочек подразумевает рост потенциала внутристрановой кооперации.

Для прогнозирования временного ряда «Численность занятых в экономике промышленности» выбрана следующая экспоненциальная функция:

X2 = 159,12e-0,03x

Используя данную функцию, с вероятностью 94,2% (R² = 0,9423) можно утверждать, что к концу прогнозного периода численность занятых в экономике составит 60,3 тыс. чел. (рис. 5). Ожидается, что численность занятых в промышленности, с учетом изменений за 2005–2021 гг., будет постепенно уменьшаться, что может быть обусловлено снижением потребности в производственном персонале при модернизации промышленности.

Прогнозные значения показателя «Объем промышленного производства» были найдены с помощью последовательной подстановки установленных значений в уравнение (1). Результаты расчетов представлены в табл. 2.

Таким образом, на практике была подтверждена классическая экономическая теория о том, что объем производства напрямую зависит от инвестиций и трудовых ресурсов. Ожидаемые значения объема промышленного производства по модели множественной регрессии демонстрируют положительную динамику, достигая к 2032 году значения в 138,8% от уровня 2021 года (или 730,1 млрд руб. в постоянных ценах).

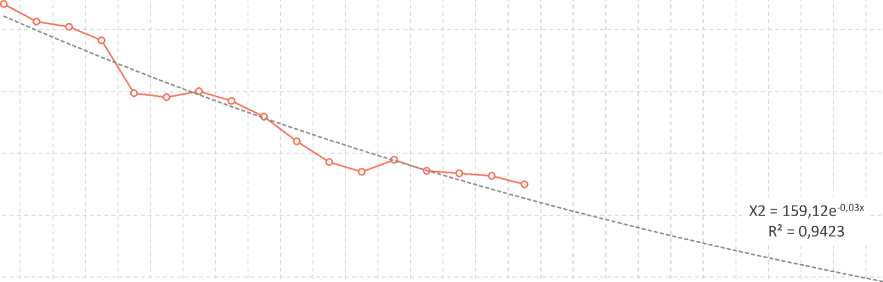
Рис. 5. Ожидаемая численность занятых в промышленности

Источник: составлено авторами.

Таблица 2. Прогнозные значения показателей, % к уровню 2021 года

Год	Объем промышленного производства,	Инвестиции в основной капитал промышленных производств	Численность занятых в промышленности
	Y	X1	X2
2022	103,4	104,5	92,7
2023	106,3	116,7	90,0
2024	109,4	129,7	87,3
2025	112,6	143,6	84,8
2026	116,0	158,4	82,2
2027	119,5	174,0	79,8
2028	123,1	190,5	77,5
2029	126,8	207,8	75,2
2030	130,6	226,0	72,9
2031	134,6	245,1	70,8
2032	138,8	265,0	68,7
Источник: составлено авторами.

Заключение

В статье представлены результаты прогнозирования объема промышленного производства. В процессе исследования была построена регрессионная модель на основе классической экономической зависимости между объемом промышленного производства, инвестициями в промышленность и занятостью в этой отрасли. Для оценки взаимовлияния показателей выполнен корреляционный анализ, по результатам которого сделан вывод о весьма тесной связи факторов. По данным протокола регресси- онного анализа составлено линейное уравнение множественной регрессии, качество которого проверено с помощью критерия Фишера и коэффициента детерминации. Качество линейной модели множественной регрессии проверено с помощью коэффициента детерминации R2 (Кинякин, Милевская, 2014). Определено, что переменными «Инвестиции в основной капитал промышленных предприятий» и «Численность занятых в промышленности» обусловлено 85,4% вариации индикатора «Объем промышленного производства».

Для определения прогнозных значений объема промышленного производства на основе экстраполяционных методов найдены ожидаемые значения внешних переменных «Инвестиции в основной капитал промышленности» (полиномиальная функция), «Численность занятых в промышленности» (экспоненциальная функция). Прогнозные значения показателя «Объем промышленного производства» были получены путем последовательной подстановки найденных значений в уравнение множественной регрессии.

Таким образом, в результате проведенного исследования были получены прогнозные значения объема промышленного производства, показывающие положительную динамику на протяжении всего наблюдаемого периода.