О прохождении межзвездных облаков через спиральный рукав дисковой галактики

DOI:

Хорошо известно, что активно процесс звездообразования в дисковых галактиках происходит в основном в спиральных рукавах [6]. Спиральные рукава включают в себя молодые звезды, области ионизированного водорода, пыль, гигантские молекулярные облака, то есть все признаки процесса формирования звезд [5]. Одновременно с этим наблюдения свидетельствуют о преимущественной концентрации молекулярного водорода в галактиках именно в спиральных рукавах [3]. Что до сих пор неясно, так это то, какую роль спиральные рукава играют в формировании и эволюции облаков молекулярного водорода.

По одним представлениям спиральные рукава, в которых происходит уплотнение межзвездного газа, выступают в роли инициаторов волн молекуляризации межзвездного газа, так что слой молекулярного газа в рукавах служит аналогом фронта волны дефлаграции [6]. Сверхзвуковое протекание газа через гравитационную яму сопровождается формированием галактических ударных волн [9]. Уплотнение газа на ударном скачке должно приводить к образованию гравитационно-связанных протооблачных структур, охлаждение газа излучением способствует достижению низких температур в облаках в десятки градусов Кельвина, при которых начинает эффективно происходить процесс молекуляризации газа на пылинках, а сами структуры затем дробятся на фрагменты (облака) вследствие образования звезд и/или гравитационной неустойчивости облачного слоя.

Согласно альтернативной точке зрения, молекулярный газ формируется повсюду в диске, а не только в рукавах, но сами рукава, рассматриваемые как протягивающиеся вдоль всего диска галактики гравитационные ямы, служат ловушкой для облаков и этим самым объясняется феномен повышенной концентрации молекулярного газа в рукавах.

В работах [1; 8] изучались стационарные потоки газа и пыли как однофазной среды в спиральном рукаве. В данной работе ставится цель смоделировать нестационарное течение — прохождение облака через спиральный рукав и проанализировать динамические и тепловые эффекты, возникающие при этом движении.

Целью работы является детальное двумерное гидродинамическое моделирование прохождения облака через спиральный рукав галактики и анализ эффектов, возникаю- щих при этом движении. Авторы исходят из простого предположения о том, что индикатором особенностей геометрии и интенсивности галактических ударных волн может служить таксономия межзвездных облаков в их окрестности. Например, о наличии или отсутствии области коротации должно быть возможным судить по сигнатурам (отличительным признакам) облаков — их характерным температурам, размерам, массам и формам сгустков, дисперсии скоростей, моментам инерции и т. п. Те статистические закономерности для размеров, ориентаций, ширин линий и скоростей молекулярных сгустков в облаках, которые могут быть обнаружены в компьютерных экспериментах, должны быть сопоставлены с наблюдениями в радиолиниях молекулярных конденсаций в реальных межзвездных облаках.

lg[n](x,y)

Рис. 1. Пространственные распределения логарифма плотности в облаке и в межоблачном газе при дозвуковом протекании газа через спиральный рукав галактики, 2Dh-модель. Число Маха М _гТ1 = 0 , 5 , глубина потенциальной ямы рукава Ф _а0 = 1 , начальный радиус облака R = 40 пк, начальная концентрация в облаке п _с = 200 см -3 . Коллаж собран из рисунков для моментов времени 1 — 0, 2 — 21 млн, 3 — 42 млн, 4 — 60 млн, 5 — 75 млн, 6 — 90 млн, 7 — 135 млн лет

1.    Физическая модель течения межзвездного газа в спиральном рукаве и геометрия течения

Физическая модель прохождения облака межзвездного газа через спиральный рукав галактики была разработана на основе следующих предположений.

• I)    Газ рассматривается как сплошная столкновительная сжимаемая среда. Динамика газа описывается в гидродинамическом приближении.

• II)    Газ считается совершенным.

• III)    Течение газа описывается как адиабатическое. Явно в используемых уравнениях гидродинамики эффекты обмена энергией межзвездного вещества с излучением не учитываются. Однако они учитываются неявно, приданием показателю адиабаты γ значения, близкого к единице. В расчетах показатель адиабаты брался равным 1,05.

• IV)    Самогравитация газа не учитывается.

• V)    Учитывается, однако, внешнее гравитационное поле, создаваемое всем распределением массы в Галактике и звездами в спиральном рукаве. Последний в модели рассматривается как конечных размеров в поперечных направлениях гравитационная потенциальная яма шириной 2а и высотой 2Ь (Ь <  а). Под поперечными к рукаву понимаем одно из горизонтальных направлений, параллельное плоскости диска (соответствующее направление связываем с осью ж), и вертикальное направление, которое задается осью z, перпендикулярной плоскости диска. Предполагается, что рассматриваемый фрагмент течения в окрестности рукава расположен далеко от центра галактики на расстояниях R _gw ^ 2а. Это позволяет на масштабах порядка 2а пренебречь неоднородностью потенциальной ямы вдоль рукава. В этом приближении яму естественно представлять бесконечно протяженным вдоль продольной оси у цилиндром эллиптического сечения.

• VI)    Сильное неравенство R _gw ^ 2а позволяет пренебречь эффектами кривизны течения и, в частности, учетом влияния центробежной силы по сравнению с силой Кориолиса [9]. Однако, как показано в [8], одномерная модель течения с учетом действия одной только гравитационной силы и без учета силы Кориолиса позволяет качественно верно воспроизводить основные особенности течения (например, предпочтительное положение ударного фронта на передней стороне ямы). Такая одномерная адиабатическая модель течения удобна уже тем, что допускает аналитическое построение решения для течения со стационарной ударной волной внутри гравитационной потенциальной ямы. В логике данного подхода силой Кориолиса в настоящей работе пренебрегается.

• VII)    Рассматриваются двумерные (2D) модели течения. Облако представляет собой однородный бесконечный цилиндр изначально круглого сечения радиуса R. В подмодели 2Dh ось цилиндра облака сонаправлена с вертикальной осью z. В подмодели 2Dv ось цилиндра облака сонаправлена с осью потенциальной ямы спирального рукава (ось у).

VIII) На входе в яму облако считается вмороженным в межоблачный газ и движется вместе с ним, проникая в гравитационную яму со скоростью, превышающей начальную скорость звука в межоблачном газе. За счет того, что облако имеет более высокую плотность, чем межоблачный газ и, соответственно, большую инерцию, в той области течения, где скорость потока переменна вдоль линии тока, возникает относительное движение облака и межоблачного газа. Если облако находится над экваториальной плоскостью, то оно не может находиться в гидростатическом равновесии. В этом случае под действием силы тяжести облако сваливается к экваториальной плоскости. Расходящееся течение, напротив, способно выносить облако вверх, в сторону от экваториальной плоскости. По мере того как облако сносится течением, оно деформируется и частично или полностью разрушается.

Таким образом, течение межзвездного газа, как межоблачного, так и газа внутри облака, описывается следующими основными уравнениями газовой динамики

+ v (pv) = o, d (pv)   _ z            x      _ d^ + V • (pv ® v + pI) =  p V ф, 9 ( p E )                      9 ф dt + V (I PE + p ]v) = p 9t,

(1) (2) (3)

Е =       + - + ф.                      (4)

(Y - 1)р    2

Здесь v — скорость; р — плотность; р — давление газа; ф — заданный внешний гравитационный потенциал; I — единичный тензор.

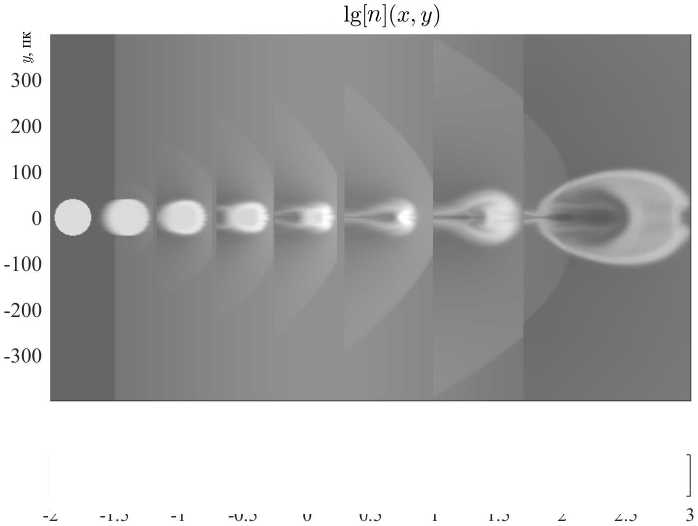
Рис. 2. То же, что и на рисунке 1, но для течения с ударной волной (число Маха M _in = 1 , 5 ), 2Dh-модель. На коллаже представлены состояния облака для моментов времени 1 — 0, 2 — 8 млн, 3 — 16 млн, 4 — 24 млн, 5 — 32 млн, 6 — 42 млн, 7 — 56 млн, 8 — 84 млн лет

2.    Одномерная стационарная модель течения

При построении аналитического решения в рамках одномерной модели течения газа в рукаве руководствуемся работами [1; 8].

Используемая в данном приближении одномерная геометрия нивелирует влияние неоднородности диска в экваториальной или вертикальной плоскостях, учитывается поле только спирального рукава.

Гравитационный потенциал спирального рукава ф _а считаем зависящим только от координаты ж. Профиль потенциальной функции ф = ф _а (ж) представляем в виде потенциальной ямы, локализованной в конечной области пространства —а <  ж <  а. Потенциал калибруем таким образом, чтобы на входе в рукав и на выходе из рукава потенциал обращался в ноль:

ф « ( — а) = ф « (а) = 0.                                 (5)

Соответственно вне ямы потенциал считаем равным нулю тождественно. Для конкретности в численных расчетах выбираем потенциал симметричным относительно ж = 0 с минимумом в центре ямы

* ( _ж ) = J - *2' ' [ 1 ^{+ cos(}У Т ) ] , ^{ж е [} - °, °];

“        ( 0,                       ж G ( -то , - °) U (°, то ).

В дальнейшем все величины соотносим с тремя размерными параметрами задачи — плотностью p _in и адиабатической скоростью звука c _s,_in межоблачного газа на входе в спиральный рукав, а также с полушириной потенциальной ямы °. Безразмерными управляющими параметрами в задаче служат относительная глубина потенциальной ямы | Ф _а0 | = ^ _a0 /c² j _n , число Маха M _in для потока межоблачного газа в точке входа в спиральный рукав и положение ударного скачка внутри спирального рукава ж ₅ ^ /°.

Для одномерного плоского движения стационарного течения совершенного газа в отсутствие силы Кориолиса система (3)–(4) интегрируется pn = J,(7)

)«2 + гЛг + * = В,(8)

• 2     (у - 1)p

pp-Y = А.(9)

Здесь J, В, А — интегралы движения, ап — компонента скорости течения вдоль оси ж. Остальные компоненты скорости в одномерном приближении считаются равными нулю. Вертикальной компонентой скорости можно пренебречь, если вертикальные движения малы по сравнению с продольным течением (всюду вне непосредственной окрестности ударного скачка это приближение полностью справедливо). Параллельная плоскости диска поперечная компонента скорости (вдоль оси ^) в рамках используемого одномерного приближения остается постоянной вдоль всего потока из-за отсутствия сил, вызывающих ее изменение. Таким образом, преобразованием Галилея ее можно полностью устранить.

В отсутствие источников массы и энергии константы J и В остаются неизменными всюду в потоке, в том числе и на фронте адиабатической ударной волны, а А терпит на ударном фронте скачок (для адиабатического скачка всегда в сторону возрастания).

Система (7)-(9) может быть сведена к одному уравнению для числа Маха M (ж) = = п(ж)/с₈(ж) [1] (под c_s = ( y p/ p ) ^{1 / 2} понимается адиабатическая скорость звука),

М ^{- 2} Y +1 ¹ М² -|--— = лм^{-2 Y +1 1} М² -|-- ¹--.          (10)

I 2 у 1/                 \2 ^гп у 1      / .                '

В выражении (10) и в последующих заглавной буквой Ф обозначается обезразмеренный потенциал Ф(ж) = *(ж)/с² _in . Коэффициент Л характеризует скачок энтропии на ударном фронте:

/ А ₊ у Y - 1 _ Г/ 2 +(у - 1)М² V / 2уМ² - (у - 1) \1 ^{Y +1}

А-/           М2 (у + 1) ) \ у + 1

Здесь и далее нижними индексами «+» и «–» отмечаем состояния сразу за и непосредственное перед ударным фронтом.

При выводе (11) используется

стандартное соотношение на адиабатическом удар-

ном скачке [4]:

М 2 = ² + ( ^Y - 1)^ 2

+    2 y M ² — (y - 1)'

Нетрудно убедиться в том, что в начальном состоянии до скачка Л = Л ₀ = 1, а всюду в потоке за скачком Л = Л 1 < 1.

Нижние индексы «0» и «1» удобно далее приписывать переменным потока, относящимся, соответственно, к области течения всюду перед скачком и всюду за ним. Тогда можно считать, что уравнение (10) с равным успехом описывает как дофронтовое, так и зафронтовое течения с точностью до переобозначения числа Маха в левой части

уравнения на М 0

Переменные формулам

или на потока

М 1 и коэффициента Л на Л ₀ или на Л 1 соответственно.

в

дофронтовой и зафронтовой областях восстанавливаются по

- = Л 2 ^ ^p in       \ ^М1п )

γ +1

•

и _л_ 1.   / М \ Y+¹

с~ = ^{Л М} (mJ  •

с ²

V" = Л s,in

1(МЛ М ;„

2 γ

γ +1

, (13)

которые вытекают из интегралов движения (7)–(9) и определения (11). Ясно, что в формулы (13) следует подставлять значения чисел Маха и коэффициента λ соответственно с индексами «0» или «1».

В итоге решение, описывающее структуру стационарного протекания межоблачного газа через спиральный рукав в одномерном приближении, строится по следующему алгоритму:

• 1)    задается начальное значение М_1; в начальной точке ж = —а;

• 2)    уравнение (10), в котором параметр λ полагается равным единице, решается численно; в зависимости от величины М_1;, меньшей или большей единицы для дозвукового или сверхзвукового входного потока, строится, соответственно, дозвуковое или сверхзвуковое решение М₀(ж); в первом случае решение протягивается вплоть до выхода из ямы в точке ж = а; во втором — решение находится только до положения ударного фронта ж = ж₅^ внутри ямы;

• 3)    по найденному значению числа Маха перед скачком М_ = М₀(ж₅^) из соотношения (12) находится значение числа Маха М+ сразу за скачком, а из уравнения (11) находится значение параметра Л = Л₁, которое теперь меньше единицы;

• 4)    значение М+ является стартовым, М1(ж₅^) = М+, для построения с помощью (10) дозвукового решения М1(ж) всюду за ударным фронтом вплоть до выходя из ямы в точке ж = а; напомним, что при построении решения в зафронтовой области в уравнении (10) используется коэффициент λ1.

3.    Численная схема для моделирования многомерных газодинамических течений

Характерные профили течения в случае дозвукового безударного и сверхзвукового течения с ударным скачком приведены в работах [1; 8].

Формально ударный фронт может находиться как на передней, то есть в области ж ₈н <  0, так и на задней стороне потенциальной ямы по отношению к натекающему потоку (ж ₅ ^ > 0), однако, как показано в работе [8], устойчивым является положение ударного фронта на передней стороне ямы. Численное 2D-моделирование полностью подтверждает это утверждение.

Одномерное решение задавалось в качестве начального невозмущенного для межоблачной среды при двумерном численном моделировании движения облака в плоскости диска (подмодель 2Dh, раздел 4).

Для численных расчетов система уравнений газовой динамики (3)–(4) приводилась к безразмерной форме с использованием трех основных размерных величин — характерного пространственного масштаба 2а = 1 кпк, начальной плотности межоблачного газа p _in = m _P n _in = 1, 67 • 10 - 24 г/см 3 и начальной скорости звука в межоблачном веществе c _s,_in = 10 км/с. Из этих трех параметров с независимой размерностью комбинируются характерное время задачи т = 2а/c _s , _/n ~ 10 8 лет, а также характерные концентрация n _in = 1 см ^{- 3} и температура T _in = n _p c 2_in /( у к _в ) = 1,14 • 10 4 К в межоблачном газе. Во всех предыдущих выкладках под т _р понимается масса протона, а под к _в — постоянная Больцмана.

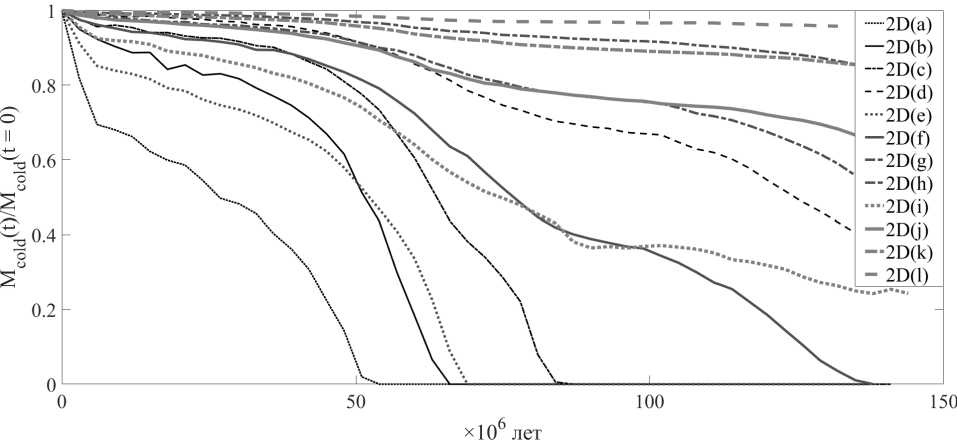
Рис. 3. Зависимость массы холодного вещества в облаке от времени нахождения облака в спиральном рукаве галактики при дозвуковом режиме протекания, 2Dh-модель. Число Маха М гп = 0 , 5 , глубина потенциальной ямы рукава Ф _а0 = 1 , значения начального радиуса облака и начальной концентрации газа в облаке для различных подмоделей приведены в таблице 2

Для облака характерными параметрами служат его радиус R и концентрация п _с , измеряемая в см ^{- 3}.

Кратко опишем основные черты используемой численной схемы [2] расчета нестационарных двумерных газодинамических течений.

Во-первых, для построения численной схемы был применен метод расщепления по физическим процессам, в соответствии с которым решение строится как решение уравнений, описывающих различные физические процессы. Во-вторых, для численного решения уравнений в частных производных гиперболического типа применялась схема неубывания полной вариации TVD, которая относится к типу MUSCL. Такие схемы эффективно подавляют нефизичные осцилляции численного решения на сильных разрывах, то есть на ударных волнах, контактных и тангенциальных разрывах. Основная идея схем MUSCL состоит в повышения точности схемы за счет изменения порядка интерполяции в пределах расчетной ячейки.

Реализованная в расчетах схема типа MUSCL имеет первый порядок аппроксимации по пространству в областях скачков и третий порядок на участках гладкого течения. Второй порядок по времени достигается посредством включения алгоритмов пересчета типа Рунге — Кутты. Для вычисления потоков величин через границы дискретных ячеек применялся приближенный метод решения задачи Римана, предложенный Хартеном,

Лаксом, ван Леером с учетом контактного разрыва [7].

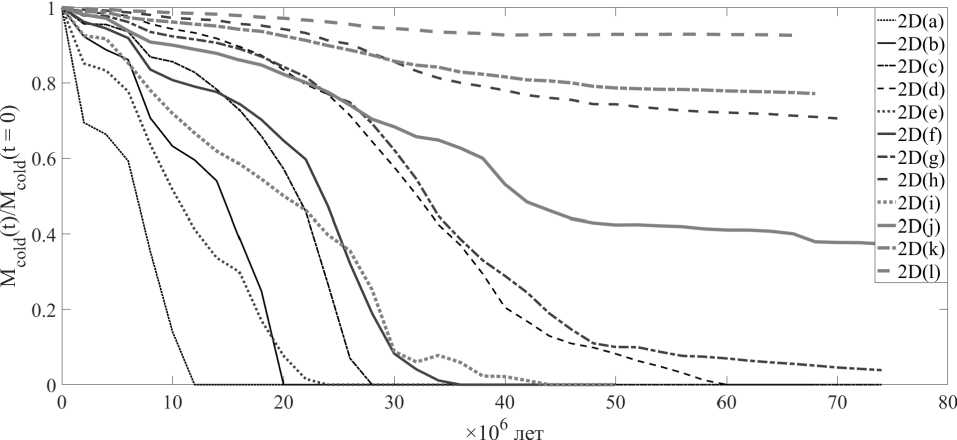
Рис. 4. То же, что и на рисунке 3, но для течения с ударной волной. Число Маха M _in = 1 , 5

Расчеты проводились на декартовых (ж, у) или (ж, z ) сетках. Размер сеток N _x х N и N _x х N _z составлял 700 х 600 ячеек (пространственный шаг 0,1 х 0,1 пк).

В таблице 1 приведены параметры численных моделей, включая использованные граничные условия, пространственное разрешение и физические параметры облака — радиус и концентрация газа в нем.

Параметры численных моделей

Таблица 1

Вариант модели	ГУ, ось X	ГУ, ось у или г	Разрешение	Радиус облака R, пк	Концентрация в облаке n c , см 3
2Dh	входные:	входные:	10–40	10,	50,
сверхзвуковой	фиксированные,	жесткая стенка,	ячеек	20,	100,
поток с УВ,	выходные:	выходные:	на радиус	40	200,
Мт = 1 , 5	свободные	свободные	облака R		500
2Dh	периодические	входные:	10–40	10,	50,
дозвуковой		свободные,	ячеек	20,	100,
поток,		выходные:	на радиус	40	200,
Мт = 0 , 5		свободные	облака R		500
2Dv	входные:	входные:	5–20	10,	50,
сверхзвуковой	фиксированные,	свободные,	ячеек	20,	100,
поток с УВ,	выходные:	выходные:	на радиус	40	200,
Мт = 1 , 5	свободные	свободные	облака R		500
2Dv	периодические	входные:	5–20	10,	50,
дозвуковой		свободные,	ячеек	20,	100,
поток,		выходные:	на радиус	40	200,
Мт = 0 , 5		свободные	облака R		500

4.    Модель 2Dh течения в экваториальной плоскости диска

В данной модели рассматривалось движение облака в горизонтальной плоскости. Параметры течения газа в межзвездной среде задавались аналитически, на основе математической модели, основные черты которой были описаны в пункте 2.

Гравитационный потенциал спирального рукава задавался в виде симметричной ямы вида (6), локализованной в конечной области пространства с полушириной а и с глубиной Ф _а0 . В рассмотренных численных моделях выбиралось Ф _а0 = 1, характерная полутолщина ямы принималась равной тому же значению, что и в одномерной модели, а = 500 пк.

В двумерной модели облако представляет собой бесконечно однородный цилиндр с осью, расположенной поперек плоскости течения. Невозмущенное состояние межоблачного газа задается как плоское стационарное адиабатическое течение одноатомного газа в соответствии с формулами, приведенными в разделе 2. Переменность параметров течения имеет место только вдоль линий тока. При натекании сверхзвукового потока газа на спиральный рукав галактики облако проходит сквозь ударный скачок. В начальный момент времени ударный фронт находится в точке x _sh = - 450 парсек на передней кромке ямы.

На рисунках 1, 2 представлены фрагменты движения облака в рукаве в различные моменты времени, позволяющие проследить эволюцию концентрации газа (изображенной в логарифмическом масштабе) как самого облака, так и окружающей среды.

По результатам серии численных экспериментов были получены зависимости относительной массы «холодного» газа от времени, которые представлены на рисунках 3, 4. Разделение межзвездного газа на «теплую» межоблачную и «холодную» облачную фазы производилось в соответствии с простым правилом, согласно которому принималось, что все вещество с температурой Т <  300 К принадлежит облачной фазе, а более разогретое вещество — теплому газу.

5.    Модель 2Dv течения в вертикальной плоскости диска

Решение одномерной задачи (п. 2) неприменимо в двумерном случае при учете вертикальной структуры спирального рукава, поэтому такое решение не использовалось для задания начального распределения потока межоблачного газа в рукаве в модели 2Dv. Изначально поток задавался как гладкий безударный и однородный вдоль ж. Затем на протяжении времени, равного динамическому времени задачи τ = 105 лет, до своего максимального значения по амплитуде «выращивалась» потенциальная яма. По истечении этого времени, в расчетной области происходит трансформация структуры газового диска, который выходит из состояния статического равновесия. В газовом диске возникают вертикальные осцилляции из-за возникающих там сил и градиентов. В случае сверхзвукового потока в газовом диске формируется сложная система ударных волн с различной интенсивностью. Первичный и наиболее интенсивный ударный скачок располагается на передней кромке потенциальной ямы.

При дозвуковом течении формируется уплотнение газа на дне ямы. Моделирование динамики газа в диске проводилось до установления квазистационарного режима течения в расчетной области. Затем на входе потенциальной ямы «формировалось» облако межзвездного газа с заданной температурой, которая подбиралась из условия равновесия по давлению с окружающей средой, скорость газа в облаке предполагалась такой же, как в окружающей среде. Положение облака в некоторых моделях было смещено относительно экваториальной плоскости.

Таблица 2

Параметры 2D-моделей

Наименование модели	R , пк	п с , см 3	Ц , М0
2D(a)	10	50	390,4
2D(b)	10	100	781
2D(c)	10	200	1 562
2D(d)	10	500	3 904
2D(e)	20	50	1 562
2D(f)	20	100	3 123
2D(g)	20	200	6 246,5
2D(h)	20	500	15 616
2D(i)	40	50	6 246,5
2D(j)	40	100	12 493
2D(k)	40	200	24 986
2D(l)	40	500	62 465

С                                ^д[п](ж, г)

-400 -200   0   200 400 600 х, пк

-2-1012

Рис. 5. Пространственные распределения логарифма плотности в облаке и межоблачном газе при дозвуковом протекании газа через спиральный рукав галактики, 2Dv-модель. Число Маха M _in = 0 , 5 , глубина потенциальной ямы рукава Ф _а0 = 1 , диска — Ф ^₀ = 5 , начальный радиус облака R = 40 пк, начальная концентрация в облаке п _с = 500 см ^-3 , начальная высота облака над экваториальной плоскостью г = 0 . Коллаж собран из рисунков для моментов времени 1 — 2 млн, 2 — 24 млн, 3 — 54 млн, 4 — 86 млн, 5 — 140 млн лет

В этой модели гравитационный потенциал включает в себя стационарный потенциал диска Ф _д (г), однородный вдоль плоскости диска и переменный в вертикальном направлении, и установившийся потенциал рукава Ф _а (х,г). Последний задается как двумерное обобщение зависимости (6) — аналитическое продолжение функции в вертикальную плоскость. Мы полагаем, что возмущению плотности в спиральной волне существенно проще распределяться вдоль экваториальной плоскости диска, чем в перпендикулярном ей вертикальном направлении, поскольку для утолщения рукава вдоль направления г газу приходится преодолевать действие силы тяжести со стороны гравитационного поля диска. Поэтому эквипотенциалями рукава мы считаем сплюснутые в вертикальном направлении концентрические эллипсы с центром в точке (ж = 0,г = 0):

где

Ф а (ж,г) = <

Ф(ж, г ) = Ф д (г) + Ф „ (ж, г),

Ф а (г)

-| Ф до | exp

( ^- I ) -

^- ^ [ 1 +^cos ( ^п V ^ж 2 + 1 — ; 2 )] , ^2+^5 <  °;

0,                              уД² + 1—_? >  °.

Эксцентриситет каждого из эллипсов задается равным 0,71, что соответствует полутолщине рукава в вертикальном направлении, равной b = 350 пк. Полутолщина диска К д выбирается равной 250 пк. Глубина потенциальной ямы составляет | Ф _а0 | = 1 для рукава и | Ф до | =5 для диска.

Отсчет времени в расчетах начинается с момента внесения облака в расчетную область. Облако задается в начальный момент времени t = 0 как множество ячеек внутри круга радиуса R, расположенного непосредственно перед спиральным рукавом. Распределение температуры в облаке задается как однородное, а давление и плотность стратифицированы, то есть находятся изначально в гидростатическом равновесии как и окружающий облако газ. Давление в каждом слое внутри облака на уровне г равно давлению на той же высоте г в межоблачном газе непосредственно возле облака. Плотность в облаке подстраивается под заданные температуру и давление из уравнения состояния идеального газа.

Облако сносится потоком межзвездного газа, натекающим на спиральный рукав галактики, и в случае сверхзвукового течения проходит через систему ударных волн, сформировавшихся ранее в потоке. В дозвуковом случае течение более спокойное, но и оно разрушительным образом воздействует на облако. На рисунке 5, 6 представлены фрагменты движения облака в рукаве в дозвуковом безударном потоке в различные моменты времени, позволяющие проследить эволюцию как самого облака, так и окружающей среды.

В результате проведенной серии численных экспериментов были получены зависимости доли сохранившейся массы холодного газа в облаке от времени, которые представлены на рисунках 7, 8. Разделение вещества на холодный и теплый газ производилось по тому же критерию, что и в модели 2Dh: температура облачной фазы не должна превышать 300 К. Как видим, модель 2Dv подтверждает результаты предыдущей модели 2Dh, когда в четырех из двенадцати рассмотренных подмоделей облака сохраняется не менее 40 % его начальной массы.

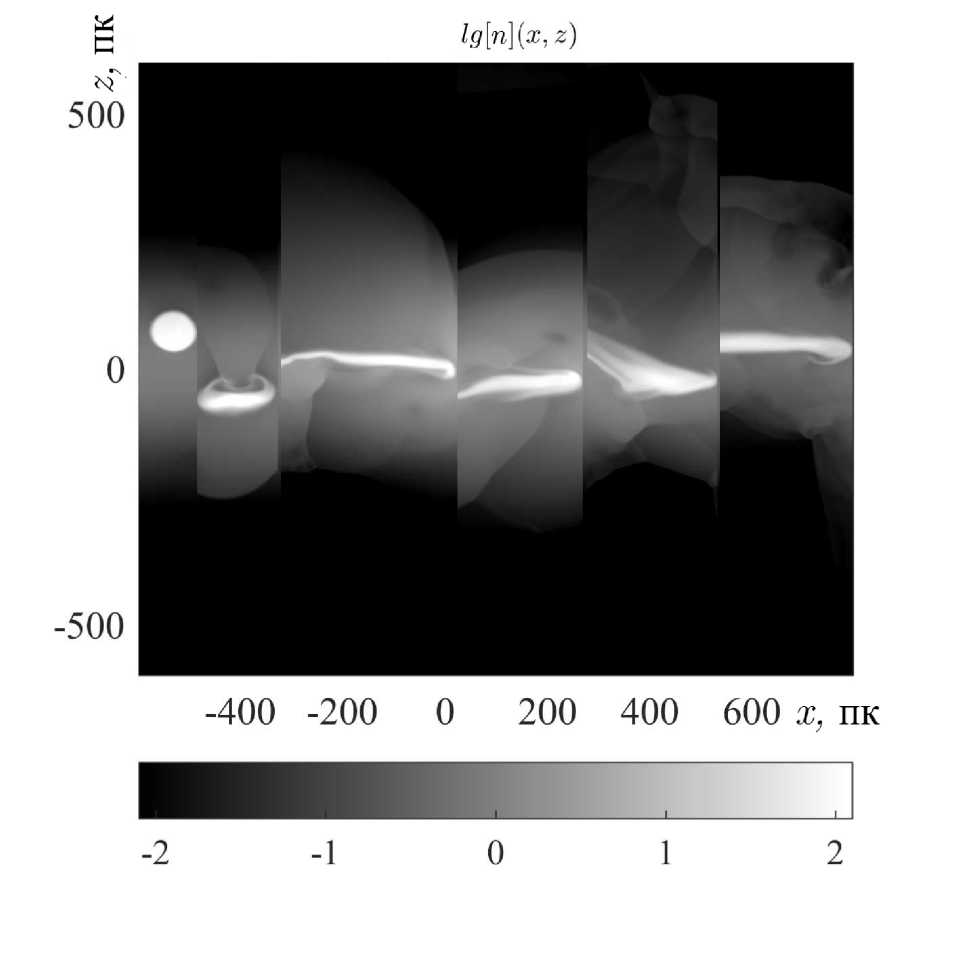
Рис. 6. То же, что и на рисунке 5, но для начальной высоты г = 80 пк.

Представлены изображения облака в моменты времени 1 — 2 млн, 2 — 26 млн, 3 — 58 млн, 4 — 84 млн, 5 — 114 млн, 6 — 146 млн лет

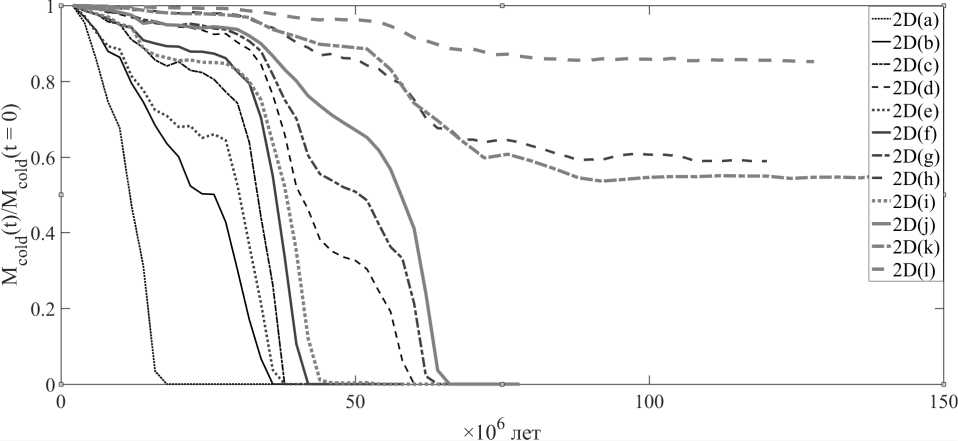
Рис. 7. Зависимость массы холодного вещества в облаке от времени нахождения облака в спиральном рукаве галактики при дозвуковом режиме протекания, 2Dv-модель.

Число Маха M _in = 0 , 5 , глубина потенциальной ямы рукава Ф _а0 = 1 , диска — Ф _й0 = 5 , значения начального радиуса облака и начальной концентрации газа в облаке для различных подмоделей приведены в таблице 2

Выводы

Расчеты показали, что по мере прохождения облака через спиральный рукав, оно, вне зависимости от того, является ли течение дозвуковым и безударным или сверхзвуковым с галактической ударной волной, сильно деформируется, вытягиваясь вдоль экваториальной плоскости диска. Облако, изначально отклоненное от экваториальной плоскости, совершает затухающие колебательные движения поперек этой плоскости. В сверхзвуковом течении с ударной волной (число Маха на входе в рукав задавалось равным 1,5) облака разрушаются полностью при малых радиусах либо при достаточно больших радиусах, но малых плотностях.

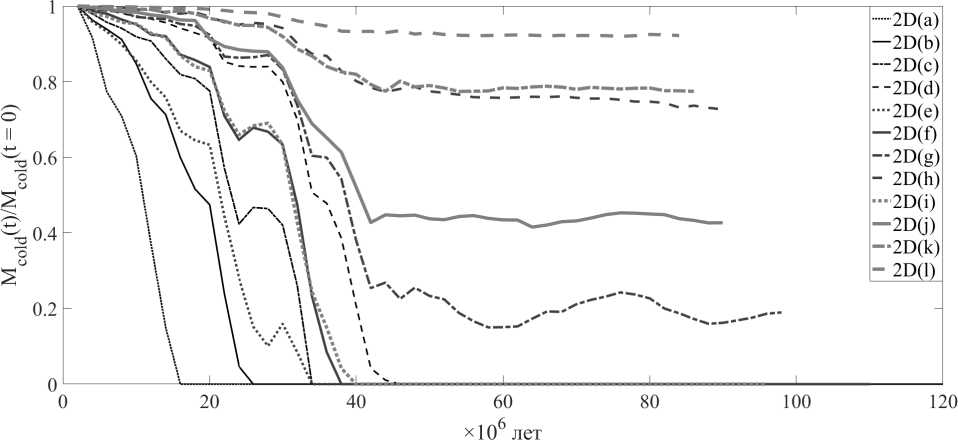
Рис. 8. То же, что и на рисунке 7, но для течения с ударной волной. Число Маха М ^п = 1 , 5

Удобно критерий того, выживает ли облако при прохождении спирального рукава или разрушается полностью, выражать в терминах массы облака. Для цилиндрической геометрии облака масса может быть определена как погонная величина, выраженная в расчете на характерную единицу длины вдоль цилиндра. В расчетах массы облака мы использовали значение погонной массы µ на 1 пк. Как следует из таблицы 2, граничное значение массы облака, при котором происходит разрушение, лежит в интервале между 3 000 и 6 000 М ₀ . Ясно, что такое определение массы облака носит весьма условный характер, и для более аккуратной оценки граничного значения массы следует использовать трехмерные модели течения.

Неожиданным результатом численных экспериментов оказался тот факт, что дозвуковое безударное течение (число Маха в этом случае на входе в рукав задавалось равным 0,5) разрушает облака интенсивнее, чем течение с ударной волной. По всей видимости, причиной этому служит тот факт, что облака в этом случае сталкиваются с характерным для дозвукового протекания газа через яму сформировавшимся массивным уплотнением газа на дне ямы.