О пространствах Гельфанда-Шилова типа S

В теории обобщенных функций, теории дифференциальных уравнений значительный интерес представляют пространства быстро убывающих бесконечно дифференцируемых функций. Это связано с тем, что при решении различных задач анализа в таких пространствах можно воспользоваться богатыми возможностями, которые представляет преобразование Фурье. Одним из таких пространств являются пространства Гельфанда — Шилова типа S [1]. Они возникли в середине 1950-х годов в работах И. М. Гельфанда и Г. Е. Шилова в ходе изучения проблемы единственности решения задач Коши

для уравнений в частных производных. К настоящему времени пространства типа S нашли многочисленные применения также в теории псевдодифференциальных операторов, частотно-временном анализе. Достаточно общий подход к определению двух классов пространств Гельфанда — Шилова типа S (в настоящей работе это пространства S ϕ и S ψ ), частными случаями которых являются как классические пространства Гельфанда — Шилова S _α и S ^β , так и их обобщения (см., например, [2]), построенные с помощью некоторых неубывающих последовательностей положительных чисел, был предложен в заметке [3]. Данная работа продолжает начатые в [3] исследования пространств Гельфанда — Шилова типа S более общего вида и линейных операторов на них и имеет своей целью подготовку необходимых сведений для дальнейшего перехода к изучению задач теории (псевдо)дифференциальных операторов и вейвлет-анализа в этих пространствах. В частности, для этого с помощью двух счетных семейств ϕ и ψ раздельно радиальных весовых функций в R ⁿ введено пространство S ϕψ , более общее, чем пространство S α^β [1, гл. 4]. Рассмотрен вопрос о его нетривиальности и дано его описание в терминах преобразования Фурье функций (раздел 2). При определенных условиях на семейство ϕ показано, что оператор периодизации непрерывным образом переводит пространство S ^ϕ в пространство периодических ультрадифференцируемых функций типа Румье (раздел 4). Изучение оператора периодизации потребовало описания функций последнего пространства в терминах убывания их коэффициентов Фурье (раздел 3).

Статья посвящена юбилею Александра Васильевича Абанина в знак восхищения широтой его научных интересов, красотой полученных им результатов и признания его большого вклада в тесное взаимодействие ростовской и уфимской школ по комплексному анализу и теории функций.

1.    Обозначения и определения Для a = (ai , . . . , an) a! = ai! • • • an!, xa = x^1 •

G Z ” , x = (x i ,... ,x n ) G R n полагаем | a | = a i + ... + a n ,

αn   α xn ,

_∂ |α|

' dx a¹ •••dx nn '

, в _п ) G Z ” обозначение a С в означает, что a j C e j

...

Для a = (a i ,..., a n ) и в = (в 1 ,

(j = 1, 2,..., n). В этом случае С в := n n=i C e j ■

Для t ^ 0 t ⁺ = max(t, 1), ln ⁺ t = In t ⁺ .

По произвольной функции g : X ^ R, где Z ⁿ С X C R n , определим функцию g* : R n ^ [ -от , + от ] по правилу: g * (x) = sup _ae Z n ( ( a,x ) — g(a)), x G R n .

Преобразование Юнга — Фенхеля функции g : R n ^ [ —от , + от ] есть функция g : R n ^ [ -от , + от ], определяемая по формуле g(x) = sup y_eR n ( ( x,y ) — g(y)).

Придерживаемся следующего определения преобразования Фурье f функции f G S(R n ): f (x) =     _n 4n f«)e i^ d^, x G R n .

Через Q обозначена совокупность всех семейств w = { w _v } V=i , состоящих из функций w _v : Z ” ^ [0, от ) таких, что для любого v G N:

• i i )    существуют зависящие от w _v числа a i ^ 0, а 2 > 0 такие, что w _v (a) ^ a i + a 2 | a | , a G Z ” ;

• i ₂ )    w _v+i (a) >  w _v (a) для любого a G Z" и lim |_a|^₊^ (w _v+i (a) — w _v (a)) = + от .

Через Q i обозначим подмножество Q, семейства w = { w _v } V=i которого удовлетворяют условию

• is)    для любого v G N существует число b^ > 0 такое, что

• Wv(a + в) C bv + Wv+i(a),   a G Z”, в G Z” П [0,1]n.
2.    О пространствах Гельфанда — Шилова типа S более общего вида и свойствах им принадлежащих функций 2.1.    Определение пространств S^, S^ и S^ . Пусть ^ = {^v}“1 g Q. Для любых v g N и m g Z. пусть m,ϕν

( f G rmm^lxe(Daf Xx)l < m , J g C (R ) • Ilf l|m,v = SUP                     < TO I xeRn,eez+,      e^v (p)

a E Z + : |a| ^ m

Положим S ^ _v •= |"|“ ₌₀ S _m,^ _v . Снабдим S ^ _v топологией, определяемой семейством норм I • ||m,_v (m g Z + ). Очевидно, пространство S ^ _v непрерывно вложено в S ^ _v+1 , v = 1, 2,... Пусть S _v = l i m S ^ _v — внутренний индуктивный предел [4] пространств S ^ _v .

По семейству ^ = {^ _v }“ 1 g Q определим пространство S ^ . Вначале по v g N, m g Z + введем пространство

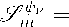
(1 + ||x||) ^m | (D ^a f)(x) | e ^ v ^(a)

< TO

f g C “ (R n ) • p m,v (f) = SUp xe R n, ae z +

Эквивалентная топология в S mψ ^ν может быть задана с помощью норм

qm,v (f ) —

SUp xe R n,ae z +, ee z +: |e| < m

|x ^e (D ^a f )(x)| e ^ v ^(a)

Пусть S ° ^v •= Q “₌-0 S m" . Наделим S ° ^v топологией, определяемой семейством норм p _m,_v (m g Z + ). Пусть S ^ = lim S ψ ^ν — внутренний индуктивный предел пространств S ψ ^ν .

По семействам ^ = { ^ _v } “=i /0 = { ^ _v } “=1 g ^ определим пространство S ^ как внутренний индуктивный предел нормированных пространств

St = О g C )• Ilf ||v

SUp x ∈ R ⁿ, a,ee z +

|xa(Def)(x)| < efiv (a)+^v (в)     °°

Пространства S ϕ , S ψ , S ϕψ построены по аналогии с пространствами Гельфанда — Шилова S α , S ^β , S α^β , соответственно [1].

Замечание. Если положить M _v (a) = e ^ ^{v (a)} для a g Z ” и M = { M _v } “=i , то получим, что S ϕ ( S ^ϕ ) не что иное, как пространство S M ( S^M ). Однако обозначения S M и S ^M представляются более громоздкими.

2.2.    О некоторых свойствах пространств Sϕ, S ψ, Sϕψ.

Теорема 1. Пусть ^ = { ^ _v } “=i ,^ = { ^ _v } “=1 g ^- Пусть функции семейства ^ не убывают по каждой переменной и lim |_a|_4M ^^1 = + то для каждого v g N.

Функция f g S (R ⁿ ) принадлежит пространству S ^ тогда и только тогда, когда существуют числа v g N и C >  0 такие, что для любого в g Z ”

^D ^e f)(x)¹ C Ce ^- ^ - ^{(ln +} Wv^xnD +V’ v ^(в) ,  x = (x ₁ ,...,x n ) g R ⁿ .

• <1 Пусть f G S G . Тогда f G S$ V при некотором v G N. Значит, для любых x G R n , а,в G Z +

| x ^a (D ^e f )(x) | С \\f ||v e ^^(a)+^ ^(в) .                                 (2)

Отметим, что благодаря неубыванию ϕ _ν по каждой переменной

|x ^Y (D ^e f )(x)| С ||f||v■ '^(a)+^ ^{v (e)} ,   a,Y G Z ^ , y С a.                    (3)

Поставим в соответствие точке x = (x i ,..., x n ) G R n точку x ⁺ = ( | x i | ⁺ ,..., | x n | ⁺ ). Тогда, с учетом (3), из (2) следует, что

PV (( a )

,ln ⁺ |x „ |)+^ „ (в)

| (D ^e f )(x)| « I f I v inf -— e * ^{v (e)} = B f B v e -~ ^(b* ^{| x 11}' a ^z I (x )

Обратно, пусть функция f G S(Rn) такова, что при некоторых v G N и C > 0 выполнено неравенство (1). Тогда для всех x = (xi,...,xn) G Rn и a = (ai,...,an), в G Z+

(D ^e f )(x)^| С Ce ^{- a 1 ln + | x} i ^|- ...-^a n

ln ⁺ lx n l+^ v (a) e ^ „ (в)

Т. е.

( | x i | ⁺ ) ^{a 1} • • • ( | x n | ⁺ ) ^a n |(D ^e f )(x)| С Ce ^(a)+^^(в) .

Тогда тем более справедливо неравенство

^| x ^a (D ^e f)(x) ^| <  Ce ^ v ^(a)+^^(e) .

Значит, f G S$ . О

В доказательстве ряда последующих утверждений точку (1,..., 1) G R n обозначаем для краткости через 1.

Предложение 1. Пусть семейства ^ = { ^ _v } V=i , ^ = {^ _v } V=i G Q i - Тогда функция f G S (R n ) принадлежит пространству S^ тогда и только тогда, когда найдутся числа v G N и C >  0 такие, что

У ^| x ^a (D ^e f )(x)| ² dx С Ce ²⁽* v ^(a)+^^(e)) , a,e G Z n₊ .                   (4)

R ⁿ

• < Пусть f G S (R n ) принадлежит пространству S ^ . Тогда найдутся числа p G N и K >  0 такие, что

• |xa(Def)(x)| С Ke*p(a)+^p(в), а,в G Z^.                       (5)

Пусть a, в G Z" произвольны. Представим интеграл JRn | x ^a (D ^e f )(x) | ² dx в виде суммы 2 ⁿ интегралов по непересекающимся подмножествам R n , описываемых n неравенствами вида | x k | С 1 или | x k | > 1. В интегралах по множествам, в описании которых участвует неравенство | x k | > 1, умножаем и делим подынтегральное выражение на x k . Тогда из (5) с учетом условий i a ) и i 2 ) имеем

У | x ^a (D ^e f )(x)| ² dx С K i e ²⁽^ p^{+1 (a)}+^ p^{+1 (в))} , a,e G Z + ,

Rn где Ki — некоторое положительное число. Итак, неравенство (4) выполнено с v = p + 1, C = Ki.

Пусть теперь имеет место неравенство (4) и а, в € Z ” произвольны. Тогда для любого x ∈ R ⁿ

\x ^a (D ^e f)(x)\ ² ^ J

R ⁿ

d n (e(D ^e f )(e)) ²

д^ 1 ... de

d£ <  E Ci^(D j (^ ^2a ))(D ^{1 -} j (D ^e f )²^ ))\d£.

^je Z + ^: j'C ¹ R n

Согласно [2], если u € S (R n ), то при любых ^,j € Z n справедливо неравенство

J \ D ^j (x ^ )\ | u(x) | dx <

R ⁿ

\2

J M|(D j u)(x)|

R ⁿ

dx.

Таким образом, с учетом неравенства (6) и пользуясь неравенством Г¨ельдера, имеем

\ x ^a (D ^e f )(x) \ ² ^ 2 n V 2У IHKD¹^ f )²«)) | de

R ⁿ

^ 2 n V 2 e c s [\t ^a (D ^e+s f)(&\\t,^a(D ^{e+ 1 -s} f)(J№ se Z + s ^ 1 R n

1                                  1

\ 2 /                                          \ 2

^ 2 n V2 E c s se Z + : s ^ 1

• ² d^l I /|^ ^a (D ^{в+ 1 - S} f )(£) \ ² del

R ⁿ

< 2 n V2C  ^   C s e ²^(^a) _e ^ v (^e+s) e ^ v (^e+ ^{1 -} s)

.

se Z ^ :s < 1

Отсюда, благодаря условиям i a ), i 2 ), получим, что при некотором C 2 > 0

| x ^a (D ^e f )(x) | ² ^ c ₂ e ²^ v+i ^(a) e ²^ v+i ^(e) .

Следовательно, f € S ^ . >

Точно теми же рассуждениями, что и в предложении 1, доказываются следующие два утверждения.

Предложение 2. Пусть семейство ^ = { ^ _v }^ i € Q i - Тогда функция f € S(R n ) принадлежит пространству S ϕ тогда и только тогда, когда существует число ν ∈ N такое, что для любого в € Z ” найдется число С в >  0 такое, что

У | x ^a (D ^e f)(x) | ² dx <  С в e ²^ ^(a) , a € Z ” .

R ⁿ

Предложение 3. Пусть семейство ф = { ^ _v }“ i € Q i - Тогда функция f € S(R n ) принадлежит пространству S ψ тогда и только тогда, когда найдется число ν ∈ N такое, что каким бы ни было a € Z ” , найдется число С _а >  0 такое, что для любого в € Z ”

У | x ^a (D ^e f )(x) | ² dx <  C _a (M ^{v (в)} .

R ⁿ

Доказательство следующего утверждения проводится по схеме доказательства теоремы 3.3 из [5]. Поэтому считаем возможным не приводить его. Отметим лишь, что оно по существу использует предложения 2 и 3.

Теорема 2. Пусть семейства ф = { ^ _v }“ 1 , Ф = {^ _v }^ i € ^ 1 - Пусть для любого ν ∈ N выполнены условия:

i ^ ) при некотором d^ >  0

^ v (a + в) >  ^ v (а) + ^ v (в) - du,

^ v (a + в) >  ^ v (а) + ^ v (в) - d v ;

• i s )    при некоторых A^B^ >  0

• 2.3 . О (не)квазианалитичности II пространства S ϕψ . В работах [6, 7] класс функций назван квазианалитическим II, если в нем отсутствует нетривиальная финитная функция, т. е. функция, отличная от тождественного нуля и равная нулю всюду вне какой-нибудь ограниченной области.

e^v(a)+^v(а) ^ A^B^a!, a € Z+ ig) существуют числа s = sv € N и b^ > 0 такие, что для всех a € Z”

^ v (2a) <  b v + 2^ v+s (a),

^ v (2a) <  b v + 2^ v+s (a).

Пусть также выполнено условие i^) существует число a > 1 такое, что для каждого v € N найдется число lv > 0, что для любого a € Z''

l v + a | a | + ^ v (a) <  ^ v+i (a), l v + a | a | + ^ v (a) <  ^ v+i (a).

Тогда функция f € S (R ” ) принадлежит пространству S p тогда и только тогда, когда f ∈ S ϕ ∩ S ^ψ .

Пусть L — некоторая (достаточно быстро растущая) положительная функция на Z ” . Она порождает класс C d (L) всех бесконечно дифференцируемых в области D С R ” функций f таких, что для любого компакта K ⊂ D найдутся положительные числа A и C такие, что

| (D ^a f)(x) | <  CA l^al L(a), x € K, a € Z ⁿ ₊ .

По L образуем последовательность чисел

L m = sup inf t ^m—a L _a , m € Z ₊ .

t>0 a& +

Определим еще функцию

0(r) = sup (|a | In r — In L(a), r> 0.

Известен следующий результат [8–11].

Теорема B. Класс C d (L) является квазианалитическим II тогда и только тогда, когда ^ ^₌i —L m = го , или, тогда и только тогда, когда / ^ 1+ 2 dr = ж.

В следующем утверждении через (exp v _v ) обозначено отображение, сопоставляющее каждому a € Z ” число e ^ ^{v (a)} .

Предложение 4. Пусть семейства ф = {фv}“!, ф = {фv}“1 g Q удовлетворяют условию iy) и пространство S* является квазианалитическим II. Тогда для каждого v g N расходится ряд

∞

Е m=1

(exp ^ф v ) m

.

^(e xp ^ф v ) m₊i

<1 Пусть в пространстве S * отсутствует нетривиальная финитная функция. Допустим, что при некотором v g N ряд (7) сходится. Тогда найдется отличная от тождественного нуля и равная нулю всюду вне какой-нибудь ограниченной области O С R n бесконечно дифференцируемая в R n функция f такая, что для любого компакта K С R n найдутся положительные числа A K и B K такие, что

| (D ^e f )(x) | С A k B^v ^(e) , x g K, в g Z + -

В частности, это неравенство справедливо и при K = Q. Поэтому, с учетом условия i i ), при некотором R >  0, зависящем от Q, для всех x g R n

|    D- f )(x)| c C i (фф , e ' ‘«’ B^e * ^- <«,

A где Ci = eai(v). Отсюда, с учетом условия iy), получим, что при некоторых s g N и C2 > 0

¹ x ^a (D ^e f ⁾(x)¹ С C 2 e ' -+s ^(a)+* -+s ^(e) , x g R n , a, в g Z ^ -

Значит, f g S * . Но по условию в пространстве S'- отсутствует нетривиальная финитная функция. Таким образом, допущение неверно и ряд (7) расходится. >

Предложение 5. Пусть для каждого v g N расходится ряд (7). Тогда пространство S ϕψ является квазианалитическим II .

< Пусть для каждого v g N расходится ряд (7). Допустим, что пространство S '* не является квазианалитическим II. Это означает, что существует нетривиальная бесконечно дифференцируемая в R ⁿ функция f , обращающаяся в ноль вне некоторой ограниченной области O С R ⁿ , и такая, что при некоторых v g N и C > 0 для любого x g R n

| x ^a (D ^e f )(x) | С Ce '^(a) e * v ^(e) , a, в g Z ⁿ ₊ -

Отсюда, в частности, следует, что

| (D ^e f )(x) | С Се ' - ⁽⁰⁾ e * - ^(e) , в g Z + -

Но тогда по теореме B f (x) =0 для любого x g R n , что противоречит допущению. >

Из предложений 4 и 5 имеем

Следствие 1. Пусть семейства ф = { ^ _v }“ i , ф = { ^ _v }“ i g Q удовлетворяют условию i y ). Тогда пространство S '* не является квазианалитическим II тогда и только тогда, когда при некотором v g N сходится ряд (7) .

2.4 . О преобразовании Фурье в пространстве Sϕψ.

Теорема 3. Пусть семейства ф = { ф _v }“ i , ф = { ф _v } V=i g Q i удовлетворяют условию i y ). Тогда отображение F : f g S '* ^ f устанавливает изоморфизм между пространствами S ϕψ и S ψ^ϕ .

<1 Покажем вначале, что отображение F действует из S ^ в S^. Пусть g G S ^ . Тогда g G S $ V Для некоторого v G N. Поэтому для всех y,^ G Z ” , x G R n справедливо неравенство

H(D ^Y g)(x) | C h g b v e ^ ^{( y )} .                             (8)

Далее, пусть £ G R n , a = (a i ,... ,a n ), в = (в 1 ,---,в _п ) G Z ” произвольны. Положим K _s := min(a s , e s ) для s = 1,..., n и к := ( ki, ..., K n ). Так как

(i£) ^e (D ^a g)(£) = ^-^ [ £ c e (D ^e-j g^D j (ix) ^a yx®dx,

^{(V2 n )} R n je Z + j Ck

| « ^e (Da^ l c        £ C e i ^  «M I Dex ^a ) l dx.

⁽V^{2 n )} n7ⁿ ^Ck   J

J^ Z + ^{j C K} R n

Отсюда, пользуясь неравенством (6), получим, что

| £ ^e (D ^a g)(£) | c

(vZ? nⁿ   £   Ce / ^{| x} (D e ^g ) ^{( x ) |} dx.

⁽V 2 ⁿ⁾ j^-. j C K    R n

Продолжим эту оценку, следуя [2, с. 371] (как и в предложении 1). А именно:

• 1)    представляем Rn_n | x ^a (D ^e g)(x) | dx в виде суммы 2 ⁿ интегралов по непересекающим-ся подмножествам R n , описываемых n неравенствами вида | x k | С 1 или | x k | > 1;

• 2)    в интегралах по множествам, в описании которых участвует неравенство | x k | > 1, умножаем и делим подынтегральное выражение на x k .

Тогда, пользуясь неравенством (8), получим, что

^9 '|3n”1

| У (D ^a g)(£)| С (^—2^ l ^ g h v e ^ ^(e)      sup e ■ ^{( a}”^) .

(vn) ⁿ                       ^=(^ ₁ ,...,^n)e z +:

^j ^ 2 ,j =1 ,...,n

Отсюда, благодаря дополнительному условию на семейство ф и условию i a ) на у, имеем при некоторых m _v G N и C 3 > 0

С (D ^a g)(£) ^| С C 3 ||g|| v У"⁺ т" We^ +iy а, в G Z ” .

Пусть n _v = max(m _v , 2). Тогда при некотором C 4 > 0

| £ ^e (D ^a g)(£) | С C 4 | g | v e ^⁺-^(e) e^ ⁺ n ^(a) , а,в G Z ” .                 (9)

Следовательно, g G S^^ n" . Итак, g G S^. Обозначим норму в S ^ ^v через || • ||( _v ) . Тогда из неравенства (9)

lgl (v₊n v ) С C 4 lgl v , g G Sy.

Отсюда следует, что отображение F действует из S ϕψ в S ψ^ϕ непрерывно.

Точно такими же рассуждениями показывается, что отображение F ^{— 1} действует из S ψ^ϕ в S ϕψ и является непрерывным. Кроме того, очевидно, линейное отображение F действует из S ϕψ в S ψ^ϕ инъективно. Таким образом, отображение F осуществляет изоморфизм между пространствами S $ и S^. О

3.    Пространство периодических ультрадифференцируемых функций типа Румье в Rn и его характеризация

Пусть C 2_n (R n) — пространство 2п-периодических по каждой переменной непрерывных в R n функций f , C “ (R n ) = C _2n (R n ) П C “ (R n ).

Каждой функции f G C 2_n (R n ) ставим в соответствие ее ряд Фурье:

f (x) <Е fa^x, X G Rn, где коэффициент Фурье fα задается формулой fa     2П.      / f (x)e-i

[0,2n]n

Пусть H = {hv}V=1

— произвольное семейство выпуклых функций h_v : Rn ^ [0, от)

с h_v (0) = 0 таких, что для любого v G N:

ji) hv (x) = hv (|X1|,..., |xn |), X = (X1, ...,Xn) G Rn;

j2) lim_x-^ h^ = +от;

j3) h_v+_i(x) ^ h_v(x) для любого x G Rn и lim_x—x(h_v+i(x) — h_v(x)) = +от;

j⁴) ^{Tv :}   ^^=(^1,

p K+l(^ln+|ai|,...,ln⁺|a_n|)-h* (ln⁺|ai|,...,ln⁺|a„|)  ,

...,a_n)eZⁿe ⁺                                                 < ^OT.

Определим пространство J(H) как внутренний индуктивный предел нормированных пространств

J (hv) = If G C“ (Rn) : Nv (f) = sup у                          xeRn,aez+

l(D^af)(x)l

ehv (a)

< ∞ , ν ∈ N.

Следуя определениям теории ультрадифференцируемых функций (см, например, [10, 12-16]), пространство J(H) можно отнести к классу пространств ультрадифференциру-емых функций типа Румье в Rⁿ, нашедших многочисленные применения в теории дифференциальных уравнений в частных производных (см., например, [17] и библиографию там) и теории операторов свертки [18–20].

Далее, следующим образом введем пространство C(H). Для каждого v G N пусть C(h_v) — пространство, состоящее из функций f G C2_n(Rn), коэффициенты Фурье которых f_a при некотором a_v(f) > 0 удовлетворяют оценке

Ifal C av(f)e^-hZ(ln+ ^^1k"^{Jn+ |an|)}, a = (ai,...,an) G Zⁿ.

Так как (благодаря условию j₂)) для любого v G N lim_x—xhRT = +от, то функции из C(h_v) бесконечно дифференцируемы. Наделим C(h_v) нормой

Pv (f )=      sup      (|/аИ ^(ln+|ai|’-’^ln+^^nD).

a=(ai,...,a_n)eZⁿ '                                 '

Далее, поскольку hv(x) ^ hv+i(x) для любого x G Rn, то pv+i(f) C pv(f) для произвольной функции f G C(hv). Значит, пространство C(hv) вложено в C(hv+i) непрерывно. При этом C(hv) — собственное подпространство пространства C(hv +i). Действительно, имеются функции из C(hv+i), не принадлежащие C(hv). Например, такова будет функ- ция

^fv+i^(x)=

Е

eh+1 (ln⁺|ai |,...,ln⁺|a_n|)_ei{a,x)

x ∈Rⁿ.

aGZn

Для нее p_v”₁(f_v) = 1, а p_v(f_v) = +го, поскольку благодаря условиям j₂) и j^) limx^_№(hV(x) — hV₊i(x)) = +ro. Пусть C(H) = UX1C(h_v)• Линейное пространство C(H) снабдим топологией индуктивного предела пространств C(h_v)•

Справедлива следующая теорема, доказательство которой проводится по той же схеме, что и доказательство теоремы 2.1 в [21], и приводится здесь для полноты изложения.

Теорема 4. Пространства J(H) и C(H) совпадают.

<1 Пусть f G J(H). Покажем, что f G C(H)• Так как f G J(h_v) для некоторого ^{V G N}’^TO             |(D^ef⁾(x)^|C Nv(f)eh^v(^ x G Rn, в G Z”.

Отсюда и из представления fa^) =(21^ J Df)(.x)e-i{ax} dx, a G Zn, в G Z”,

[0,2n]n получим, что для любых a = (ai,..., an) G Zn, в = (в1, • • •, вп) G Z” .                           ehv (в)

^{|fa| СNv(f)}(ЖМШ^П.

Отсюда следует, что

Ifal С Nv(f)e^{-hV(ln+ |a1} |”-”^{ln+ |an|)}, a = (ai,...,an) G Zn.

Следовательно, f G C(h_v) и, значит, f G C(H). Кроме того, из последнего неравенства следует, что p_v(f) С Nv(f) для f G J(h_v). Значит, пространство J(h_v) вложено в C(h_v) непрерывно. Но тогда и J(H) вложено в C(H) непрерывно.

Пусть теперь f G C(H). Тогда f G C(h_v) для некоторого v G N. Значит, Ifal С pv(f )e^{-K(ln+ |ai|}’-’^{ln+ |an|)}, a = (ai,..., an) G Zn. (10)

Таким образом, при любых a = (ai,...,an) G Zn, в = (в1, •••,в_п) G Z” .                          ehv (в)

^|fa| ^ ^(f a               a         .

Эта оценка означает, что f G С^П(Rn). Далее, пользуясь неравенством (10), условием j^), для произвольных x G Rn, в = (в1,..., в_п) G Z” имеем

|(De f )(x)| С       £       |f|(|«1|* )в1 ••• (|a„| + )вп a=(ai,...,a„)eZn

С p_v(f)      ^£      e^{-hv(ln+ |ai|}’-’^{ln+ |a}n^|)(|a₁|⁺)^ei••• (|an|⁺)^en

(ai,...,an)eZn sup      (в1 ln+ |ai|++вп ln+ |an|-h*+1(ln+ |ai|,...,ln+ |an|))

С T_vp_v(f)e(^al-."-^an)6Zⁿ

С     (f) tan^^-hV+i (t))

Отсюда, воспользовавшись предложением 1 из [21], получим, что

|(D^ef)(x)| С Tvpv(f)e^hv+1(e), x G Rn, в G Z”.                     (11)

Итак, f G J(h_v+1) и, значит, f G J(H). Из неравенства (11) следует, что

Nv+1(f) С Tvpv(f), f G C(hv).

Но тогда и вложение C(H) в J(H) непрерывно.

Из доказанных утверждений следует совпадение пространств J(H) и C(H). >

4.    Об операторе периодизации в S ϕ

Отметим, что если f G S(Rn), то для любого в € Z+ ряд E«eZ”(D^ef )(x + 2na) сходится равномерно на компактных подмножествах Rn. Поэтому его сумма принадлежит классу C“(Rn) и, очевидно, является 2п-периодической по каждой переменной функцией.

Определение. Пусть ^ = {^_v}v=i G Q. Определим на S^ оператор периодизации P, полагая

(Pf )(x) = £ f (x + 2na), x G Rn.

aeZn

Теорема 5. Пусть семейство H = {h_v}“! выпуклых функций h_v : Rn ^ [0, от) с h_v(0) = 0, помимо условий ji)-j4), удовлетворяет дополнительным условиям:

• j5) для любого v G N существует число c_v> 0 такое, что

• hv(a + в) С Cv + hv+1 (a), a G Z+, в G Z+ П [0,1]n;

• j6) для любых v,m G N найдется число c_v,_m> 0 такое, что

• n

hv+i(a) > Cv,m + hv (a) + £m ln(1 + ak), a = (ai, ...,an) G Z^. k=i

Пусть семейство ^ состоит из функций ^_v := h_v|z+ , v =1, 2,...

Тогда оператор P действует из S ^ в J (H) и является непрерывным.

• <1 Согласно следствию 1 из теоремы 1 в [3] отображение F : f G S^ ^ f устанавливает изоморфизм между пространствами S ^ϕ и Sϕ . В частности, отображение F действует непрерывно из S ^ϕ в Sϕ . Причем, как следует из концовки доказательства теоремы 1 в [3], каково бы ни было v G N для любого m G Z+ при некотором C_m,_v> 0

Ilf ^m,v +1 < Cm,vPm+2n,v (f), f G S ' .                        (12)

Далее, для любого a G Zn

(4Гa          / £ f (x + 2na)e-i(^ax>dx

^{( J} [aX]n aeZn

• =        £ f f (x + 2na)e^-i(a,x>dx =        [ f (x)e^-i(a’x>dx

(2n)n        I              ’               (2n)n J M > a^Z [a,2n]n                                         Rn

Следовательно,

(Pf )(x) = —R- £ /(-a)e«^a'^x>, x G R".

^(V2n)aezn

Заметим, что в силу неравенства (12), в частности,

I x^ef(x) I < Cm,vPm+2n,v (f ■     ^(в), x G Rn, в G Zn.

Из этой оценки следует, что

If(-a)| ^ Cm,vPm+2n,v (f У-^^ ^¹^"^ln^{+ |an|)}.

Отсюда, с учетом того, что ^_v+i = h_v+i|z+ , имеем

| рJ < Km,vPm+2n,v (fe^^^ |a1|,-,ln+ |an|), где Km,v = -gmnVn ■ Следовательно, ((Pf )a)aeZn 6 C(hv+1) и

Pv+l^Wa)_a&n ) < Km,vPm+2n,v (f), f 6 S ' •

Но тогда согласно концовке доказательства теоремы 4 Pf 6 J{h₊+2) (и, значит, Pf 6 J(H)), причем, при любом m 6 Z+

NV+2(Pf ) < Tv+1Km,vPm+2n,v (f), f 6 S *^v.

Из этого неравенства следует, что линейный оператор P действует из S^ в J(H) непрерывно. >