О рациональном распределении пористости при кручении бруса прямоугольного поперечного сечения

DOI:

Вопросы оптимального проектирования конструкций приобретают в последнее время все большую значимость и актуальность. Имеется ряд направлений оптимизации. Одним из них является управление свойствами внутренней структуры материала. Теоретические исследования по возможности управлять упругими характеристиками при кручении (модулем сдвига G) рассматриваются в работах К.А. Лурье [5]. Пример решения рационального распределения модуля сдвига G по прямоугольному сечению бруса при кручении представлен в работе М.И. Рейтмана и Г.С. Шапиро [6]. Другим направлением является регулирование свойств материала уровнем пористости. В настоящей работе рассматривается задача распределения пористости по сечению бруса прямоугольного профиля при кручении с целью наиболее рационального использования материала без потери несущей способности. Большой вклад в изучение свойств пористых материалов внесли Ю.А. Кашталян, С.В. Белов, У.Д. Кингери, Д.О. Бутарович [1–4]. Пористые материалы обладают рядом специфических свойств: пониженной теплопроводностью, повышенной звукоизоляцией, хорошей ударной вязкостью. Кроме того, в теплоэнергетике пористые материалы являются единственно возможными жаропрочными материалами, выполненными из керамики или пористых металлов, полученных методом порошковой металлургии.

Представляет интерес рассмотреть задачу чистого кручения бруса прямоугольного поперечного сечения, выполненного из материала (стали) пористой структуры с переменной по сечению пористостью. Ограничимся случаем упругого деформирования, полагая, что максимальное касательное напряжение в брусе τ _max не превышает предела текучести материала при сдвиге τ _T . Известно, что упругие характеристики материала (модуль сдвига G , а также напряжение начала текучести σ _T ) являются функциями пористости материала [1–4]. Сглаживая результаты экспериментальных данных для пористой стали методом наименьших квадратов (МНК), получаем зависимости G ( p ), σ _T ( p ), τ _T ( p ) в виде:

G = a ₁ + a ₂ p + a ₃ p ² , σ _T = b ₁ + b ₂ p + b ₃ p ² , τ _T = c ₁ + c ₂ p + c ₃ p ² .

Значения коэффициентов a_i , b_i , c_i ( МПа ) сведены в таблицу 1 для интервала пористости от 0 до 0,43. На рисунке 1, а , б , в приведены графики функций (1), (2), (3) соответственно. Точками обозначены экспериментальные значения упругих характеристик.

Поскольку переменная по сечению пористость приводит к неоднородности свойств материала, используем теорию кручения неоднородных стержней с введением функции напряжений Φ [7]. Исходное уравнение задачи кручения имеет вид:

∂ ₍ 1 Φ ∂ x G ( p ) ∂ x

8   1  ф

) + ^∂ ( ^{1  Φ} ) =- 2 θ ,

∂y G(p) ∂y где G(p) – модуль сдвига как функция пористости. В свою очередь, пористость – функция координат p = p(x, y); θ – относительный угол закручивания.

Таблица 1

Таблица значений коэффициентов, полученных методом наименьших квадратов

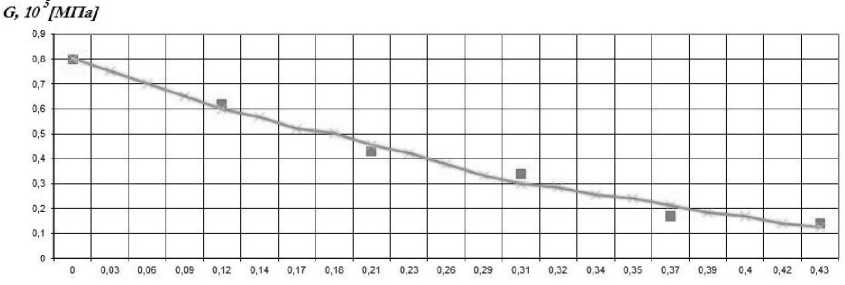
Рис. 1, а . Зависимость модуля сдвига от пористости

а 1	0,805⋅105	b 1	190,31	c 1	109,87
а 2	-1,737⋅105	b 2	-893,15	c 2	-515,67
а 3	0,359⋅105	b 3	1226,49	c 3	708,15

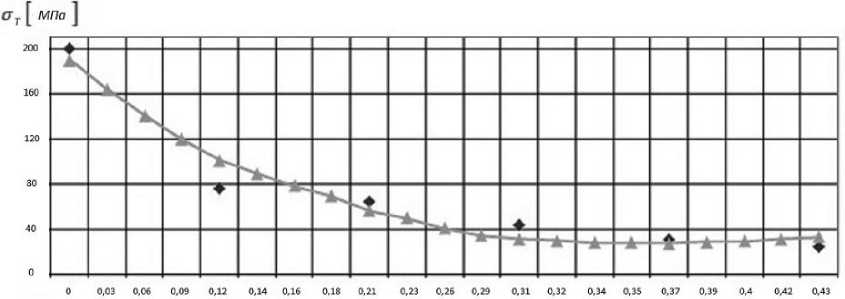
Рис. 1, б. Зависимость предельных нормальных напряжений от пористости

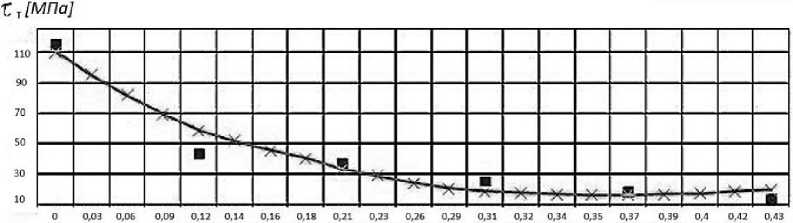
Рис. 1, в . Зависимость предельных касательных напряжений от пористости

Граничное условие на внешнем контуре L для функции напряжений Ф следующее:

Ф L = 0.

Решение краевой задачи (4), (5) заменим поиском минимума эквивалентного ей функционала:

I =и

A

1^т---

² G ( x , У )

2 дФ) ( дФ ) д x J ⁺^д у ,

- 29Ф > dxdy.

Для поиска минимума функционала (6) воспользуемся методом конечных элементов, для чего разбиваем сечение бруса на прямоугольные треугольники (двумерные симплекс-элементы) с катетами, ориентированными по x и y (рис. 2, б ).

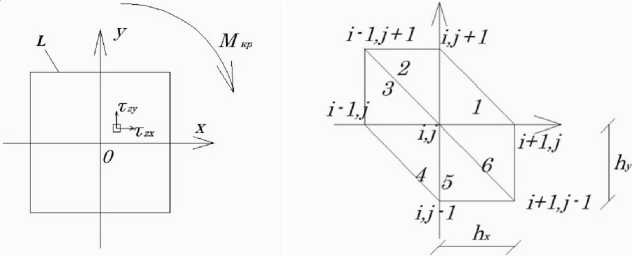
Рис. 2, б. Схема разбиения сечения на двумерные симплекс-элементы

Рис. 2, а . Расчетная схема

При этом функционал (6) минимизируется на множестве функций сопрягаемых элементов, которые при линейной сплайн-аппроксимации на границах сопряжения элементов удовлетворяются автоматически.

Тогда для узла i, j получим I = ^Ii, i = 1, 2,..., 6, где

И

A i

^ _-------

² G ( x , y )

дФ i ) (дФ i ) д x J \ д y ,

- 29Ф > dxdy.

Аппроксимируем функцию напряжений Ф в каждом элементе линейным сплайном

^Ф k = « к 1 ⁺ « к 2 ^{Х +} « к 3 У ’ ^k = 1, ², ™, ⁶,                                ⁽⁸⁾

где a k 1 , а k ₂ , а k ₃ - выражаются через узловые значения функции напряжений Ф j . .

Для первого элемента имеем:

xy ij

«11         ij L V ‘j        ‘+1’ j' h        '1         ‘, j+1 ’ hx                 hy

1 ,            , дФ

« 12 = г( ^Ф ‘ +и^-Ф j ) = !T^;

h_x                д x

, -Ф ) = —.

13                     ‘, j + 1           ‘I hy               дy

Для четвертого элемента:

xy ij

⁴¹ ‘j К ^V ‘ ^{- 1,} j         ‘ ’ j'      К ^V ‘ ’ j ^{- 1}          ‘ ’ j ⁷;

hx                  hy

« 42 = h^j -^-u) ;

a₄₃ = — (Ф - Ф J = — .

⁴³ h ⁽ i ’ j       i ’ j ^{- 1)}     д y

Для остальных элементов коэффициенты получаются перестановкой индексов.

Подставляя зависимости (8) в функционал, интегрируя и используя процедуру Ритца [7], получаем систему уравнений:

ф n ⁺¹= — [ф ^п r +ф ^п, D +Ф ^П-1,F +Ф ^П .' C -40)

Фу a Фi,j+1 Bj +Фi-1,jDj +Фi,j+1 Fj + Фi+1,jCj 4Vj, где

11  1

A, = — (—7 +—?) + ^{j            2}     h y ²

Gh

1        J

x

Bj =     + j   G4hy2   G5hy2 ,

C j =

1 G 2 h y ² 1

G 1 h X +

1    11   1     1     1

++(—7 +—7) +7 +7

^G 3 ^hx ^{2    G} 4 ^hx ^{2    h}y ^{2     G} 5 ^hy ^{2    G} 6 ^hx ^{2 ,}

1 D = 1 + 1 F = 1 + G ₆ h³’  ^j   G 4 h X + G 3 h²’   j    G 1 h y   G 2 h²"

Систему (11) решаем по методу итераций, проверяя условие:

Max\ФS,У"ФS,-,■ 1|

При этом найденное значение функции напряжений Ф позволяет вычислить составляющие касательного напряжения по формулам:

∂Φ ∂Φ

, τ zy = -      .

∂ y , ^y ∂ x

Соответственно касательное напряжение в произвольной точке сечения определится зависимостью:

τ=V zx zy и должно подчиняться условию: τ τT, (15) где τT – функция пористости.

На основании (15) корректируется пористость по сечению по схеме последовательных приближений.

В качестве примера рассмотрим брус прямоугольного поперечного сечения 10 × 5 см, выполненный из пористой стали. Разобьем его на 100 частей по большей стороне и на 50 по меньшей. Таким образом, h_y = 0,001 м и h_x = 0,001 м.

Для рационального распределения пористости изначально задаемся произвольной постоянной пористостью ( р = 0), при этом G = const. Решая систему уравнений (11) для фиксированного относительного угла закручивания θ = 0,03, получаем таблицу значений Ф _ij (рис. 3, а ) и τ (рис. 3, б ).

Достоверность полученного результата для сплошного материала ( р = 0) подтверждается сравнением решения данной задачи с точными формулами теории упругости, где значение момента получилось равным 6,87 кНм (погрешность решения 0,21 %), значение касательных напряжений на большей стороне 111,7 МПа (погрешность решения 2,2 %) и значение касательных напряжений на меньшей стороне 88,8 МПа (погрешность решения 2,9 %).

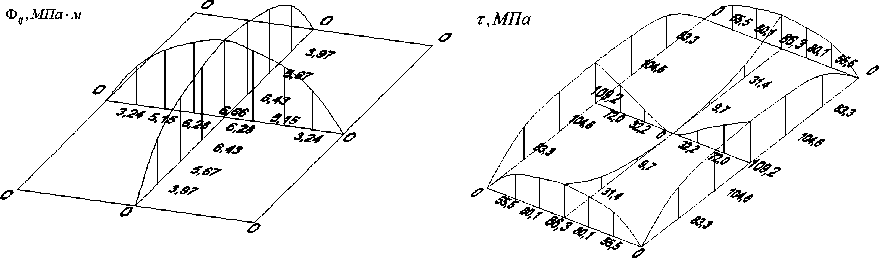
Рис. 3, а. Распределение значений функционала            Рис. 3, б. Распределение значений по поперечному сечению           касательных напряжений по поперечному сечению

По значениям касательных напряжений τ находим значения пористости р исходя из (3) в соответствии с условием (15) и ограничениями, задаваемыми техническими возможностями производства 0 <  p < 0,4.

Получив сетку значений распределения пористости р по поперечному сечению, находим поле значений модуля сдвига G по (1) во втором шаге и заново решаем задачу.

По известным значениям функционала Ф _ij вычисляем крутящий момент как:

N

M_кр = 2 ∑ Φ _срh_xh_y ,                                     (16)

k = 1

где N – число сдвоенных элементов в сечении.

Процедуру последовательных шагов заканчиваем тогда, когда при заданном θ выполнится условие:

M + i - M.

M

i + 1

•100% < 0,5%

.

Результаты приближений сведем в таблицу 2.

Таблица 2

Результаты итерационных вычислений

№ приближения	Значение крутящего момента, кНм	Средняя пористость	Значение M, - M, , —--—, % M
0	6,8554	0	–
1	5,49278	0,15942	24,80747
2	4,93786	0,21006	11,23807
3	4,67816	0,2317	5,551328
4	4,5464	0,2424	2,898117
5	4,47284	0,2486	1,644593
6	4,43036	0,25214	0,958839
7	4,4045	0,25433	0,58127
8	4,38384	0,25623	0,47127

При оценке полученных результатов мы видим, что достигли необходимого значения на 8-м приближении.

Характерные значения окончательного рационального распределения пористости показаны на рисунке 4.

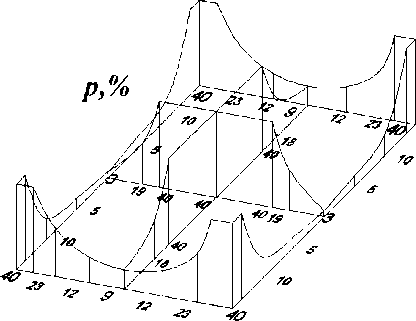
Рис. 4. Рациональное распределение пористости по поперечному сечению

При этом значения Ф .j иллюстративно представлены на рисунке 5, а , а значения т - на рисунке 5, б .

Таким образом, в зоне минимального уровня касательных напряжений (вблизи угловых точек и в центре) пористость выше, а в зоне максимального уровня касательных напряжений (в серединах сторон) – ниже некоторого среднего значения. Кроме того, значение крутящего момента для бруса с рационально подобранной пористостью по поперечному сечению (Мкр = 2,19192 кНм) на 31,3 % выше, чем для бруса со средней пористостью (Мкр = 1,6700 кНм), что свидетельствует о рационализации распределения пористости по поперечному сечению.

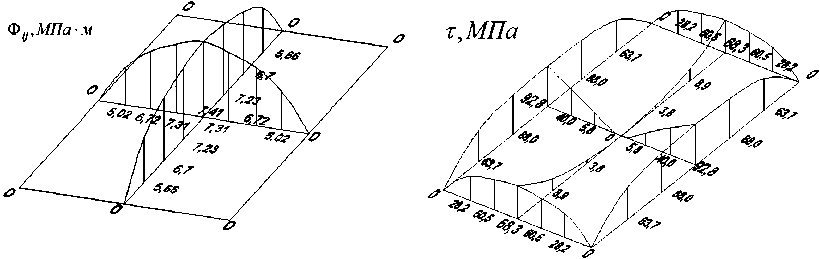
Рис. 5, а . Значения функционала, соответствующие рациональному распределению пористости

Рис. 5, б . Значения касательных напряжений, соответствующие рациональному распределению пористости