О рациональных приближениях алгебраических чисел \root 3\ of {D}
Автор: Тасоев Ботаз Георгиевич
Журнал: Владикавказский математический журнал @vmj-ru
Статья в выпуске: 3 т.3, 2001 года.
Бесплатный доступ
В статье усиливается результат К. Рота о рациональном приближении для алгебраических чисел \root 3\of D.
Короткий адрес: https://sciup.org/14318028
IDR: 14318028
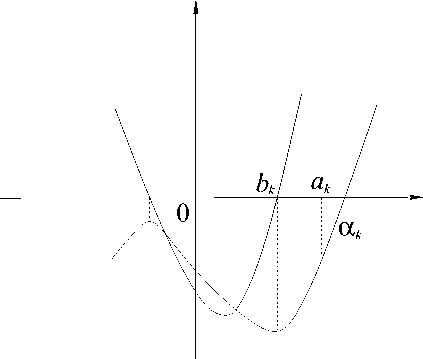
Список литературы О рациональных приближениях алгебраических чисел \root 3\ of {D}
- Ленг С. Введение в теорию диофантовых приближений-М.: Мир, 1970.-103 с.
- Тасоев Б. Г. О рациональных приближениях к некоторым бесконечным цепным дробям.-МПГУ, Москва, Автореф. дисс. на соиск. уч. степ. канд. физ.-мат. наук, 1997.
- Фельдман Н. И. Приближения алгебраических чисел.-М.: МГУ, 1982.-311 с.
- Хинчин А. Я. Цепные дроби.-М.: Наука, 1978.-112 с.
- Шидловский А. Б. Диофантовы приближения и трансцендентные числа.-М.: МГУ, 1982.-264 с.
- Шмидт В. Диофантовы приближения.-М.: Мир, 1983.-228 с.
Статья научная
