О расчете надежности восстанавливаемых систем с невосстанавливаемым резервом

Рассмотрим систему из n + 1 идентичных элементов, из которых только один является рабочим, а остальные n – ненагруженными резервными элементами. Система функционирует таким образом, что после отказа рабочего элемента производится его замена (восстановление системы) одним из резервных элементов, при этом восстановление отказавшего элемента не производится и в дальнейшей работе системы он участия не принимает. Система функционирует до тех пор, пока не откажет последний n + 1 элемент. Смысл такого рода резервирования заключается в том, что хотя каждый отказ элемента, стоящего на рабочем месте, фиксируется как отказ системы, но быстрая замена отказавшего элемента позволяет форсированно перевести систему в состояние работоспособности, поддерживая ее высокую готовность к функционированию [1].

Начав работать, система последовательно попадает из состояния работоспособности в состояние отказа, затем опять в состояние работоспособности и т. д., причем за время функционирования система может побывать только в конечном числе состояний H0, H1, ...,H2n, H2n +1. Пусть система находится в работоспособном состоянии, если она находится в «четных» состояниях H0, H2, ... , H2j, ..., H2n ; система находится в состоянии отказа, если она находится в «нечетных» состояниях H1, H3, ..., H2j+1, ..., H2n+1. Та- ким образом, H2 j – состояние работоспособности, в которое система переходит после j-го отказа и j-го восстановления; H2 j+1 - состояние отказа, в которое система переходит после j-го восстановления и, соответственно, j+1-го отказа.

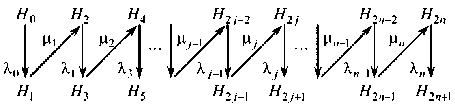
Рис. 1. Граф переходов восстанавливаемой системы

Граф переходов описанной выше системы показан на рис. 1. На графе все нечетные (нижние) состояния являются состояниями отказа системы, а все четные (верхние) состояния – состояниями работоспособности. Введем обозначения

N = 2 n + 1; X j = Ю 2 j ; Ц j = ® 2.j - 1 ;

ц_1 = 0 ; 0 < j < n, тогда граф переходов можно представить в другом виде (рис. 2), что соответствует графу переходов системы для «схемы гибели» [1, 2].2

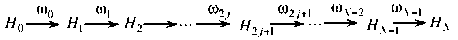
Рис. 2. Преобразованный граф переходов («схема гибели»)

О расчете надежности восстанавливаемых систем с невосстанавливаемым резервом

Решая систему дифференциальных уравнений, отвечающих графу на рис. 2, вероятность P k ( t ) того, что система в момент времени t находится в состоянии H_k [1] при начальных условиях P о ( 0 ) = 1; P k ( 0 ) = 0;1 <  k <  N ;

для случая, когда все юi различны, получим к-1     k      p^itit

P k ( t ) = П ю _У Е ------ ; 1 <  k <  N -1;     (1)

j ^{- 0} i ^{- 0} П ( “ , - “- )

l - 0 l ^ i

N -1 N -1        ,,^-l,) i '

P n ( t ) - 1- П    Z e --------.           (2)

j-0   i-0 “,П(“I - “J l-0 l ^ i

Если замена отказавшего элемента на резервный производится с одной и той же интенсивностью h независимо от номера отказа системы, а интенсивности последовательности отказов одинаковы и равны X , т. е.

“ 2. j + 1 -h ; 0 <  j <

N –3

то в этом случае

; “ 2 j -X ;

получаем

0 <  j <

N –1

для четных k

(Xh) 2 . ^P‘^(t) T-h) * |

e

к

X t Z (-1 Ус i-0

k k ²

k

¹ [ (h-x) - ] 2^— i ₊

--1

—1 2

-1+i ( k .V — i V k 2 J

k — 1 + ( - 1 ) ²

k

--1

e ^—H t Z C i -0 :

k k2 —+i

k

KiHz-X t b

— i — 1

k        11/

— i - 1 k

2       )

Г ,

для нечетных k ( 0 <  k <  N )

Х⁽Хц ) ₂ .

^{Pk (} t ) ^- (X-h) k 1

e ^—X t

k - 1

Z ( - 1)‘C.

i - 0

k _— 1                  k — 1

V [ (h-x) t 1 2^— i

k —1 •          1      1

⁺ i | k - 1

I

i !

+

В условиях рассматриваемой модели значение коэффициента готовности равно

K - lim K ( t ) . (7) t ^^

Среднее время T_N функционирования системы до ее окончательного отказа (состояние H_N ) и среднее время T ^ пребывания системы в состояниях работоспособности определяются по выражениям

N –1 1 N –1 1

T n - Z — , T ^ - Z — (для четных i ). (8) k - 0 ^ю i k - 0 “ i

Вероятность того, что система в интервале времени [ 0; t ] еще функционирует (либо работает, либо производится замена отказавшего элемента), т. е. вероятность того, что система за интервал [ 0; t ] не попадет в конечное состояние H N , определяется по формуле S N ( t ) - 1 - p_n ( t ), где вероятности p_N ( t ) для соответствующих случаев определяются по выражениям (2) и (5).

Пусть имеется система из оного основного элемента и пяти резервных элементов, находящихся в ненагруженном режиме. Интенсивность отказов работающего элемента равна X- 0,05 1/ ч , интенсивность подключения резервных элементов на место отказавшего (интенсивность восстановления) равна ц - 5 1/⁴. Определим, что в момент времени t - 30 ч система будет работоспособной.

Система может находиться в двенадцати состояниях: H ₀ , H ₂ , H ₄ , H ₆ , H ₈ , H ₁₀ – состояния работоспособности; H ₁ , H ₃ , H ₅ , H ₇ , H ₉ , H ₁₁ – состояния отказа, причем H ₀ – состояние системы, характеризующееся тем, что основной элемент работает безотказно; H ₁ – состояние системы, в котором основной элемент отказал и началось подключение первого резервного элемента (восстановление системы); H ₂ – состояние системы, в

k + 1

+ ( - 1)^

k - 1

e ^—h t Z C. i - 0

k - 1

k -1 .

+ i

k —1 .

KhzXO - Ll- 1

k - 1

r ,

i !

^{PN (} t ) ^{- 1-}F x n

n ( X t ) ^{n -1}_v.

H e Z, ,,Z i ^) j^cn -1+ j l —7 i -0 ^{( n -} i )! j -0            k ^ц-Х,

X

j

I +

л n +1

+(-1) n+1      e ц-Х

. n —1 fl Я?^- i ^—1 L ( 11 Y I

-h - ( M t ) _____ ^C^{n h} I

Z^    Zc cn + j      r i-0(n-i-1)!j-0 Ац-ХJ I

-L

Используя формулы (1)–(5), для соответствующих вариантов можно определить вероятность пребывания системы в момент времени t в одном из состояний работоспособности K ( t ) :

N –1

K ( t ) - Z P_k ( t ) (для четных k ).

k - 0

котором закончилось подключение первого резервного элемента, и система продолжает работать безотказно и т. д.; H ₁₁ – состояние окончательного отказа системы, когда отказали последовательно все пять резервных элементов.

Так как n - 5, N - 2 n + 1 - 11, то, воспользовавшись формулами (3)–(5), для вероятностей p_k ( t ) того, что в момент времени t система находится в состоянии H k ( k - 0, 1, ..., 11 ) , получим

P 0 ( t ) - e ^-X t ,

P 1 ⁽ - )=Д^{( e -X} t ^{- e}" ) ,

P 2 ( t I ’T^ ( « [ ( H-X ) t - 1 ] + « -^H ' ) , -, ( H ^-X )

P 10 ( t ) ^-

e "^X t

— ( ц-Х ) ⁵ 1 ⁵ —⁵ ( ц-Х ) ⁴ 1 ⁴ + 120           24

Е.А. Алёшин

+ 2 ( ц-Л ) 3 t ³ - 35 ( ц-Л ) ² t ² + 70 ( ц-Л ) t - 126 ] - ^— e ^Ц t 24 ^(ц-Л) 4 t ^{4 + (ц-Л)} 3 t ^{3 +} "2" ^(ц-Л) 2 t ^{2 +} + 56 ( ц-Л ) t + 126 ) .

Вероятность того, что система в момент времени t = 30 будет работоспособной в соответствии с формулой (6) равна K (t = 30) = 0,986. Вероятность того, что система в момент времени t = 30 попала в состояние окончательного отказа H11 равна pN (t) = p11 (30) = 0,004. Среднее вре мя работы системы (8) TN = 220 , а среднее время пребывания в состояниях работоспособности Т^ = 120.