О расчете полосы температур при переходе жидкость - стекло для двухкомпонентных неорганических стекол

Современное материаловедение ставит во главу угла поиск и разработку функциональных материалов с прогнозируемыми свойствами. К таким материалам относятся и стекла, аморфные сплавы, полимеры. Они обладают отличительными свойствами, которые позволяют использовать их в электронике и других областях.

Особое место в изучении неорганических стекол, полимеров, металлических сплавов и других аморфных веществ занимает исследование процесса перехода жидкость — стекло. Научные работы по данной тематике показывают наличие общих, независимых от природы соединений, закономерностей, универсальных правил, по которым происходит стеклование этих материалов [1-3].

Наличие выявленных общих для указанных выше материалов закономерностей позволяет высказать предположение о том, что процесс перехода жидкость — стекло для стеклообразующих жидкостей различной природы может быть описан единой теорией, разработка элементов которой соответствует основной задаче данной области физики конденсированного состояния.

Вместе с тем замечено, что для отдельных классов веществ при температуре стеклования T g замораживается подвижность кинетических единиц, обладающих различным характером взаимодействия между собой. Для линейных аморфных полимеров процесс стеклования связан с релаксационным процессом и потерей сегментальной подвижности при температуре стеклования, а в неорганических стеклах с принципиально иной структурой этот процесс связан с химической релаксацией и замораживанием процесса переключения валентных химических связей.

При охлаждении стеклообразующей жидкости в области температуры стеклования резко возрастает ее вязкость. Принято считать, что переход жидкость — стекло происходит при достижении предельной вязкости п _g= П ( T _g):

П ~ const ~ 10¹² Па • с . ⁽¹⁾

Выражение (1) является приближенным правилом постоянства вязкости при температуре стеклования T , , т. е. это соотношение можно рассматривать как условный феноменологический критерий стеклования. В литературе по тематике исследования установлено, что температура стеклования T g для большинства рассмотренных стекол соответствует значениям, при которых вязкость п _g достигает величины в пределах 10¹¹-10¹² Па^с, т. е. приблизительно равна значению в выражении (1) с допустимой погрешностью [4]. Такая закономерность более отчетливо прослеживается, если рассматривать материалы одного класса.

Если обратиться к попыткам определить температурную зависимость вязкости аморфных веществ с применением уравнения Аррениуса, то становится очевидно то обстоятельство, что оно неэффективно ввиду зависимости энергии активации вязкого течения в области температуры стеклования от температуры и вследствие того возможностью расчета только в очень узком интервале T [4].

Температурная зависимость вязкости для маловязких жидкостей описывается известным уравнением Френкеля [1, 5]

( U 1 П = n o exp I      I •

V RT J

Однако уравнение (2) не применимо для стеклообразующих расплавов, поскольку в данной формуле энергия активации U вязкого течения учитывается как постоянная величина, тогда как для рассматриваемых расплавов данная такая энергия в области перехода жидкость — стекло значительно зависит от темпера-

туры U = U ( T ). Таким образом, с учетом вышесказанного считаем, что для выра-

жения температурной зависимости вязкости для аморфных веществ, таких как

рассматриваемые стекла, более удачным будет применение уравнения Вильям-

са — Ландела — Ферри (ВЛФ) [1, 3, 6]:

In a_T = - Q

^T - ^T g   ,

T - T g + C 2

a _ n(T) ~ r(T), aT=ПТ)=TQ

где параметр aT называется относительной вязкостью, τ — время структурной релаксации. Эмпирический параметр C1 является безразмерной величиной, а C2 имеет размерность температуры. Полученные в настоящей работе и ранее значения эмпирических параметров уравнения ВЛФ приведены в таблице 1 [7, 8]. Также на основе этих данных получены другие параметры стеклующихся систем. Результаты расчетов показывают, что величина C1 приблизительно остается универсальной постоянной для различных классов веществ, в том числе исследуе- мых силикатных и оптических стекол.

Параметры уравнения ВЛФ (3) С ₁ и С ₂ и характеристики процесса стеклования стекол [8, 9]

Таблица 1

Вещество			С 1	С 2 , K	T g, K	δT g , K	f g
№	Стекло,	мол. %		Натриево-силикатные стекла
	Nа 2 O	SiO 2
1	15	85	36	430	782	11,9	0,028
2	20	80	36	390	759	10,8	0,028
3	25	75	35	355	739	10,1	0,029
4	30	70	35	322	721	9,2	0,029
5	33	67	35	304	712	8,7	0,029
6	35	65	35	291	705	8,3	0,029
№	Стекло,	мол. %		Свинцово-силикатные стекла
	PbO	SiO 2
1	20	80	19	543	808	28,6	0,053
2	30	70	21	501	765	23,9	0,048
3	33,3	66,7	22	490	749	22,3	0,045
4	35	65	30	688	746	22,9	0,033
5	40,1	59,9	27	562	728	20,8	0,037
6	42,1	57,9	34	660	702	19,4	0,029
7	45	55	18	333	697	18,5	0,056

8	48	52	33	552	675	16,7	0,030
9	49,6	50,4	22	301	675	13,7	0,045
10	50	50	50	856	673	17,1	0,020
11	55	45	81	1272	646	15,7	0,012
12	60	40	188	2780	640	14,8	0,005
13	63	37	93	1180	632	12,7	0,011
14	66	34	26	262	618	10,1	0,038
15	66,6	33,4	26	263	619	10,1	0,038
16	68	32	49	559	627	11,4	0,020
№	Стекло,	мол. %		Халькогенидные стекла
	As	S
1	12,5	87,5	12	81	319	6,7	0,083
2	15	85	13	102	326	7,8	0,077
3	17,5	82,5	12	87	338	7	0,081
4	20	80	14	113	352	8,1	0,072
5	25	75	15	121	379	8,3	0,069
6	27	73	17	175	387	10,1	0,058
7	28,6	71,4	19	217	392	11,3	0,052
8	30	70	19	211	396	11,2	0,053
9	32,5	67,5	18	210	404	11,6	0,055
10	35	65	22	287	419	12,9	0,045
11	36,7	63,3	23	304	423	13,4	0,044
12	37,6	62,4	26	364	432	13,8	0,038
13	39	61	26	351	441	13,7	0,039
14	40	60	27	356	450	13,2	0,037
15	40,6	59,4	28	379	446	13,7	0,036
16	41,1	58,9	26	360	444	13,7	0,038
17	42,1	57,9	27	361	440	13,3	0,037
18	42,7	57,3	27	360	434	13,3	0,037

Следует отметить, что данное уравнение ВЛФ находится во вполне удовлетворительном согласии с известным уравнением Фогеля — Фулчера — Таммана:

Л^Г ) = A ■ exp

.

г - Г

Далее приводятся результаты расчета кинетического критерия стеклования в двухкомпонентных силикатных и халькогенидных стеклах.

Результаты расчета полосы температур

Уравнение ВЛФ с учетом постоянства параметров C 1 и C 2 удобно тем, что при преобразовании его в уравнение прямой, где y = — ( T — T _g) / ln a _T, а переменная x = ( T — T _g). Графики, построенные в данных координатах по известным данным о температурной зависимости вязкости стекол, показывают достаточно отчетливую линейную зависимость y ( x ). Так, для двухкомпонентных силикатных и оптических стекол были построены соответствующие графики, которые показали применимость уравнения ВЛФ к описанию температурной зависимости вязкости. На рисунке 1 представлен график зависимости y(x) для стекла As-S по данным о вязкости базы SciGlass [9].

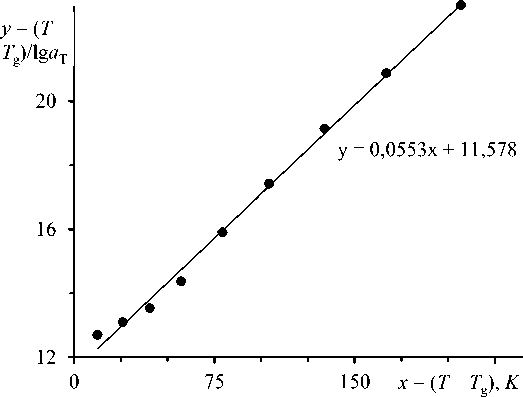
Рис. 1. Температурная зависимость вязкости As-S стекол в координатах, соответствующих уравнению ВЛФ. Использованы данные [9].

Содержание As — 32,5 мол. %.; S — 67,5 мол. %

Графики такого типа дают возможность получить приближенную оценку параметров уравнения ВЛФ С ₁ и С ₂ из данных уравнения прямой (табл. 1).

Модель делокализованных атомов Сандитова [7, 10, 11] предлагает следующее толкование одного из параметров уравнения ВЛФ: C 1, представляет собой обратную величину доли флуктуационного объема f _g при температуре стеклования:

Су = —.                        (5)

1 _f ^g

Величина f g , являющаяся одним из основных параметров модели делокализованных атомов, слабо зависит от природы вещества. Флуктуационный объем ΔV e обусловлен тепловыми смещениями атомов аморфного вещества [10, 11]

AVe = Ne AVe , где Ne — число делокализованных атомов, Δve — элементарный флуктуационный объем, необходимый для предельного смещения атома из равновесного положения. Величина fg, рассчитанная по данным о параметре С1, как и следовало, лежит в узком диапазоне значений до 10% [7, 10] (табл. 1):

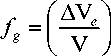
® const® 0.03 - 0.08 •

t — T

g

В области стеклования при уменьшении температуры вследствие замедления молекулярной подвижности и перегруппировки атомов структура расплава не успевает следовать за уменьшением температуры. В области Tg резко возрастает вязкость расплава, а также время релаксации т(Т), которое связано в уравнении стеклования со скоростью охлаждения расплава q = (dT/dt). Данная связь согласно релаксационным теориям [12-17] играет решающую роль в процессе стеклования. Бартеневым [12] из общих соображений на основе экспериментальных данных было предложено уравнение, которое связывает эти величины в выражении qTg — C,                        (6)

где т _g — время структурной релаксации при температуре стеклования T _g, C — эмпирический параметр с размерностью температуры. Скорость q в данном уравнении подразумевает абсолютную величину скорости изменения температуры I q I при охлаждении расплава или при нагревании стекла. Соотношение (6) хорошо зарекомендовало себя при определении зависимости температуры стеклования от скорости охлаждения, при использовании методов релаксационной спектрометрии других стеклообразных материалов и других аморфных веществ [16].

Волькенштейном и Птицыным также была разработана строгая теория о по- ведении кинетических единиц, которые могут находиться в двух состояниях, разделенных энергетическим барьером [13]. Решение кинетического уравнения показывает, что стеклование системы происходит при некоторой температуре Тg, когда происходит замораживание доли частиц в возбужденном состоянии. Тем- пература Tg в данной теории соответствует условию.

dT ^

-- —-- dT J T—T

В указанной теории стеклования роль кинетического критерия перехода жидкость-стекло выполняет уравнение стеклования [11]:

qTg — 3Tg •(8)

Величина 5Tg, предложенная данным образом профессором Немиловым [14], характеризует температурный интервал перехода от жидкости к стеклу при охлаждении.

В данной работе предлагается оценка этого параметра уравнения стеклования 5 T _g для двухкомпонентных силикатных и бескислородных халькогенидных стекол, для чего предлагается обратить внимание на указанные выше формулы (3) и (7).

Подстановка зависимости т (T) из ВЛФ (3) в выражение (7) приводит к соотношению qTg

С 2 , С 1

при сопоставлении которого с уравнением стеклования (8) можем записать формулу для расчета полосы температур 5 T g с использованием полученных нами значений параметров уравнения ВЛФ:

S T = С 2 .                      (10)

g    _{С 1}

У исследуемых стекол (табл. 1) рассчитанная таким образом величина δ T _g составляет Na 2 O — SiO 2 : 8.3 — 11.9 K ; PbO — SiO 2 : 10.1 — 28.6 K ; As — S: 6.7 — 13.8 K .

Второй параметр уравнения ВЛФ С 2 равен отношению f g к коэффициенту теплового расширения флуктуационного объема при температуре стеклования β f [10]

f

С = g^, 2   Pf но произведение βf ∙Tg также является однозначной функцией fg:

вТ = f; ln 1 fg).            <12)

Из равенств (5), (10) и (11) с учетом (12) следует, что параметр уравнения стеклования (8) δTg можно определить температурой стеклования и долей флуктуационного объема fg:

f

^ T g =

g T. tn(Vfg) g

Ранее мы оговаривали, что материалы, особенно стекла одного класса, имеют значения f_g ≈ const , поэтому следует предполагать, что между величинами δ T _g и T _g должна наблюдаться линейная корреляция. Из рисунков 2–4 видно, что у всех исследуемых полоса температур δ T g , в пределах которой происходит переход от жидкости к стеклу, линейно зависит от температуры стеклования T _g. Однако следует сказать, что не для некоторых исследованных составов, которые здесь не приведены, такой закономерности не наблюдается с достаточной достоверностью.

Об относительном постоянстве угла наклона зависимости полосы температур δ T _g от температуры стеклования T_g (13) также говорит достаточно малый разброс значений доли флуктуационного объема f g (табл. 1).

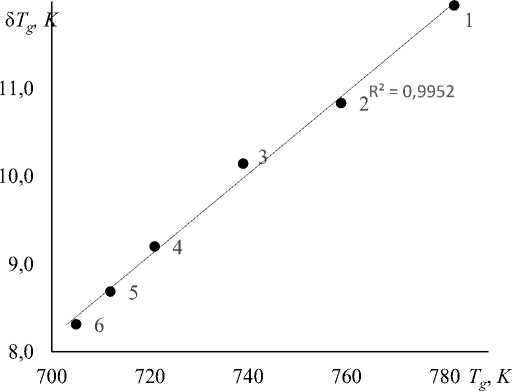
Рис. 2. Линейная корреляция между полосой температур δ T_g , характеризующей интервал стеклования, и температурой стеклования T_g стекол системы Na₂O — SiO₂ Номера точек соответствуют номерам стекол в таблице 1

δ T g , K

25,0

15,0

5,0

600         650         700         750         800 T_g , K

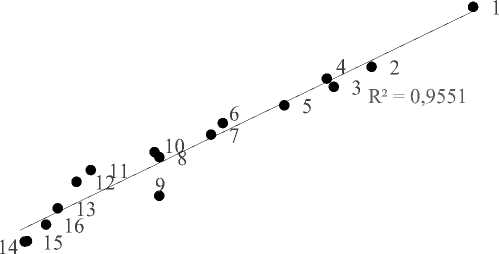
Рис. 3. Линейная корреляция между δ T _g и T _g для стекол PbO — SiO₂.

Номера точек соответствуют номерам стекол в таблице 1

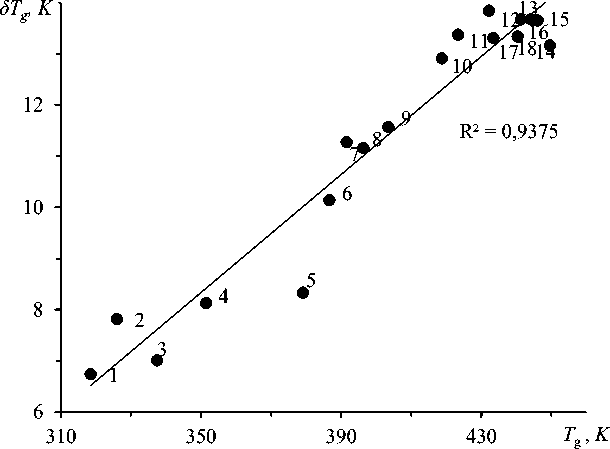
Рис. 4. Линейная корреляция между δ T g и T g стекол системы As-S.

Номера точек соответствуют номерам стекол в таблице 1

Заключение

Переход жидкость — стекло с точки зрения релаксационной теории стеклования имеет ярко выраженный релаксационный характер. При охлаждении расплава в области температуры стеклования перегруппировки атомов, групп атомов становятся замедленными, в связи с чем изменение структуры не успевает следовать за уменьшением температуры. Данный подход в процессе стеклования жидкости отдает решающую роль соотношению между временем структурной ре- лаксации τ и скоростью охлаждения расплава q = dT/dt. Взаимосвязь этих величин лежит в основе уравнения стеклования: qτg = δTg.

В работе представлен расчет полосы температур δТ _g, в пределах которой жидкость переходит в стекло, по рассчитанным нами данным об эмпирических параметрах уравнения Вильямса — Ландела — Ферри C 1 и C 2 . У исследованных двухкомпонентных натриево-, свинцово-силикатных и халькогенидных стекол величина δТ _g находится в диапазоне от 6,7 K до 28,6 K .

Было предположено, что малый разброс значений доли флуктуационного объема f g для исследованных стеклообразных систем одного класса дает основание для наличия линейной зависимости полосы температур δТ _g от T_g . Результаты расчетов относительно близко демонстрируют данное предположение на графиках, хотя и не для всех материалов, что требует дальнейших исследований в данном направлении.

Уравнения типа уравнения Бартенева (6) имели успешное применение не только для процесса перехода жидкость — стекло, но и для других релаксационных процессов [12]. К таким процессам можно отнести термостимулирование электрической деполяризации аморфного полимера, которое описывается подобным соотношением [19].