О распараллеливании решения краевых задач на квазиструктурированных сетках
Автор: Свешников Виктор Митрофанович, Рыбдылов Батор Доржиевич
Статья в выпуске: 3 т.2, 2013 года.
Бесплатный доступ
Рассматриваются технологические аспекты решения краевых задач на предлагаемых квазиструктурированных сетках специального вида. Их особенностью является то, что и макросетка в расчетной области, и подсетки в подобластях являются структурированными и прямоугольными сетками, что обеспечивает создание экономичных структур данных и эффективное применение численных алгоритмов. В то же время, результирующая квазиструктурированная сетка является адаптивной к неоднородностям внутри области и к сложной конфигурации внешней границы, что достигается путем регулировки плотности узлов подсеток и локальной модификации сетки вблизи криволинейной границы. Существенным является то, что подсетки могут быть несогласованными. Решение ищется предлагаемым вариантом метода декомпозиции, который основан на отдельной аппроксимации краевой задачи на интерфейсе и в подобластях. Распараллеливание проводится путем группировки подобластей в объединения с целью балансировки загрузки процессоров. Приводятся оценки эффективности распараллеливания на примере решения модельной задачи на различном числе вычислительных ядер, различных сетках и объединениях.
Краевые задачи, параллельные алгоритмы и технологии, декомпозиция области, квазиструктурированная сетка
Короткий адрес: https://sciup.org/147160504
IDR: 147160504 | УДК: 519.67
Текст научной статьи О распараллеливании решения краевых задач на квазиструктурированных сетках
Адаптивные квазиструктурированные сетки, рассматриваемые в настоящей статье, имеют ряд преимуществ по сравнению со структурированными и неструктурированными сетками. По отношению к первым они дают возможность избавиться от лишнего числа узлов, которые зачастую вводятся лишь для поддержки структурированности, а по отношению ко вторым имеют гораздо более простую структуру данных небольшого объема, что позволяет более эффективно строить численные алгоритмы. Важным является то, что подсетки, из которых состоит результирующая квазиструктурированная сетка, могут быть несогласованными. Это дает возможность автономной аппроксимации решаемого дифференциального уравнения в подобластях, на которые разбивается расчетная область. Сетки, обладающие данным свойством, рассматривались в работах Ю.А. Кузнецова [1], Ю.В. Василевского [2], К. Бернарди [3] и других авторов. Характерным для этих работ является применение метода конечных элементов и множителей Лагранжа для поиска решений в подобластях и на границе их сопряжения (интерфейсе). В настоящей работе рассматривается конечно-разностный подход [4], основанный на непосредственной аппроксимации уравнения Пуанкаре–Стеклова на интерфейсе при помощи дискретных функций Грина, который дает простой параллельный алгоритм для поиска решения.
Процесс распараллеливания алгоритмов решения краевых задач на квазиструктури-рованных сетках имеет некоторые особенности, связанные с равномерной загрузкой процессоров. Обычно используемое при распараллеливании отображение одна подобласть – один процессор в этом случае недопустимо вследствие того, что подсетки в подобластях могут быть несогласованными, то есть иметь существенно различное число узлов. Это приводит к разбалансировке загрузки процессоров. Для её выравнивания предлагается группировать подобласти в объединения, имеющие приблизительно одинаковое число узлов, что привносит некоторые изменения в технологию распараллеливания, так как в объединение могут входить как подобласти, не требующие межпроцессорных пересылок, так и подобласти, для которых они необходимы. В последнем случае обмены происходят с процессорами-соседями, номера которых должны быть предварительно определены и сохранены. С целью исследования эффективности данного нового подхода был проведен цикл численных экспериментов, результаты которых приводятся ниже.
1. Алгоритмы построения квазиструктурированных сеток и решения на них краевых задач
В этом разделе мы кратко приведем сведения по алгоритмам построения ква-зиструктурированных сеток и решения на них краевых задач, которые необходимы для изложения дальнейшего материала. Более подробную информацию по данному вопросу можно почерпнуть в работах [4, 5].
Расчетной областью, в которой ищется решение ф ( х ) краевой задачи, будем называть замыкание G = G U Г , где G - открытая, односвязная, ограниченная область в двумерном вещественном пространстве, в которой задано решаемое уравнение
Lu = f , x е G , (1)
а Γ – граница, на которой заданы краевые условия lu = g, x еГ. (2)
Здесь L, l – соответственно операторы уравнения и граничных условий, а f, g – задаваемые функции. Отметим, что задача (1), (2) рассматривается как в декартовых x, y , так и в цилиндрических x = r, y = z координатах соответственно для плоских и осесиммет- ричных областей.
В прямоугольнике R = {о < x < Dx 0 < y < Dy }, где Dx, Dy - заданы, описанном во- круг расчетной области ( G ⊂ R ), построим прямоугольную равномерную макросетку
Q h
-- -- D D
,
Xi = IHx, Yj = JHy, I = 0, Nx, J = 0, Ny, Hx = , Hy = ^y xy где Nx , Ny – заданные целые числа, с шагами Hx , Hy >> h ( h – максимальный шаг сетки, на которой аппроксимируется задача (1),(2)). Фактически мы тем самым проводим декомпозицию на подобласти . Среди них будем различать – внешние,
– внутренние, – граничные подобласти, которые соответственно не содержат точек , содержат только точки , содержат точки и . Точки пересечения координатных линий x = XI , y = YJ макросетки являются макроузлами, которые обозначим как , а отрезки координатных линий, принадлежащие расчетной области, образуют границу сопряжения подобластей γ или интерфейс.
В замкнутых подобластях G^J, Gj'2^ построим равномерные прямоугольные подсет- ки
^hk = К = XI + ik hxk , У jk = YJ + Jk hyk , ik = 0, nxk , Jk = 0, ny,k } к XI+1 - XI ,. Yj+1 - Yj с шагами hxk =---------, hyk =-------. Здесь введена единая нумерация подобла- nxk ’ n y,k стей и подсеток по индексу . По аналогии с подобластями будем различать под сетки двух типов: внутренние Qh1k и граничные Qh2k.
Граничные подсетки Qh2k подвергаются локальной модификации, состоящей в сдвиге приграничных узлов на границу Γ , в результате которой они преобразуются в подсетки Qh(^. Объединение подсеток Qh1k и Qh^ образует результирующую ква- зиструктурированную сетку Ωh .
На границе сопряжения подобластей γ введем сетку ω h , не содержащую макроузлов Г;: to h = {( x i , У; ) е Y , ( x, , У, ) * T p , i = 1, Nra } , где N y - известное целое число. Дополнив to h макроузлами T p , образуем сетку (5h = { to h , T 1 , T 2 ,^TP } .
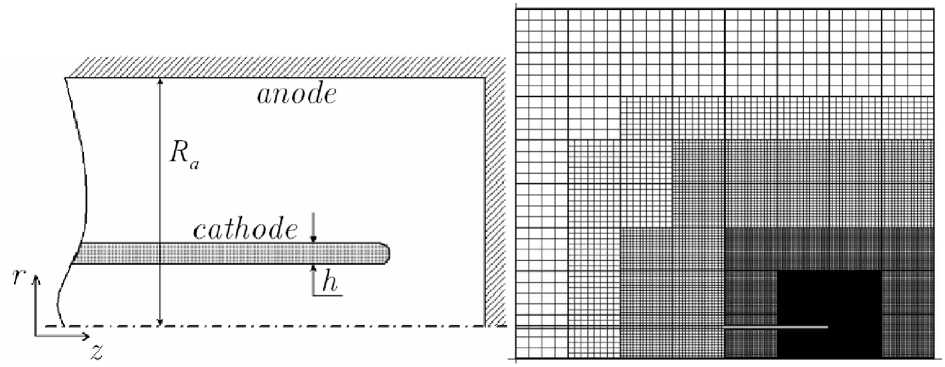
На рис. 1а приведен пример геометрии практической задачи, которая представляет собой так называемый сильноперенапряженный промежуток, предназначенный для формирования мощных электронных пучков в приборах сильноточной электроники. Ее особенностью является то, что отношение максимального размера к минимальному составляет 35000 (h=0,0001, R a =3,5). На рис. 1б показана квазиструктурированная сетка для расчета данного прибора, которая стягивается к острию катода, то есть подобласти, где требуется получить детальное решение.
а)
б)
Рис. 1. Пример геометрии сильноперенапряженного промежутка и квазиструктурированная сетка
Краевая задача (1),(2) в подобластях G I ^,) , G^J методом конечных разностей, конечных элементов или конечных объемов на сетках Q h(1k , Q h( ^ заменяется приближенной задачей, причем на интерфейсе ставится граничное условие Дирихле
ϕh γ =vh , где ϕh , vh – приближенные значения функций u , v , ( v – след ϕ на γ ).
Для отыскания v h применяется метод декомпозиции расчетной области на подобласти, сопрягаемые без наложения, предложенный и подробно изложенный в работе [4]. Он основан на непосредственной аппроксимации уравнения Пуанкаре–Стеклова
f* ^ + ^ - = 0 (3)
(an J (an J при помощи дискретных функций Грина в узлах сетки ωh и исходного уравнения (1) в макроузлах. Здесь n – нормаль к γ , верхние индексы показывают принадлежность объекта к различным подобластям. Результатом является система линейных алгебраических уравнений
Av h + b = 0
относительно функции v h с невырожденной квадратной матрицей A и известным вектором b . Ее решение осуществляется итерационным методом вида
vh-+1) = a(av;", vh"), (4)
где n=0,1,… – номер итерации, а Λ – матрица, определяющая конкретный алгоритм, то есть здесь используется лишь сам вектор v hn ) и действие Av hn ) матрицы на вектор.
Этим условиям удовлетворяет, например, семейство быстросходящихся итерационных методов в подпространствах Крылова [6]. На каждом шаге данного итерационного процесса необходимо вычислять величины
( n )_(,4(+)т< n ,+ f^—W n" )!
f h , i = ( d h T h ) i - ( d h T h ) , (5) в узлах сетки У h , где d h + ) , d^ - конечно-разностные операторы, аппроксимирующие нормальные производные в уравнении (3).
2. Параллельные технологии решения задач
Распараллеливанию подлежит итерационный процесс (4) по подобластям, который занимает подавляющую часть времени решения всей задачи. Важным звеном в технологической цепи решений по достижению эффективности распараллеливания является отображение сеточных данных на вычислительную сеть. Обычно принятый способ отображения «одна подобласть – один процессор» в данном случае не эффективен, так как подобласти могут содержать существенно различное число узлов, в которых вычисляются значения искомой функции (в дальнейшем – счетных узлов), что приводит к дисбалансу загрузки процессоров.
Поэтому подобласти группируются в объединения Um , m = 1, M , где M - известное число, с целью обеспечения приблизительно равной загрузки процессоров. Для этого в каждое объединение Um = ^ Qhmk) включаются такие подсетки Qhmk), которые давали k бы в сумме Nm = ^Nk(m) число счетных узлов такое, что Nm « NU , где NU - заданная k величина, а Nkm) - число счетных узлов в подобластях.
Алгоритм группировки подобластей для идеальной балансировки должен строиться на решении задачи линейного программирования. При этом может оказаться, что в объединение включаются не только соседние подобласти, но и подобласти, разделенные подобластями из других объединений. Последнее обстоятельство может привести к значительному увеличению объема самых медленных операций, а именно операций пересылки в системах с разделенной памятью.
Обмены не происходят между соседними подобластями одного объединения, в связи с чем был принят следующий алгоритм построения объединений . Задается число N U , которое должно быть больше или равно максимальному числу узлов в подобласти. Для каждой свободной, то есть не включенной ни в одно объединение, подобласти просматриваются свободные соседи. Количество узлов просмотренных подсеток суммируется. Если после просмотра -й подсетки в m -м объединении окажется, что N m > N U , то процесс группировки заканчивается, причем при N m - N U > 0.5 N kkm ) последняя подсетка не включается в данное объединение.
Строится отображение «одно объединение – один процессор». На текущем процессоре на каждой n -й итерации выполняются следующие вычислительные работы:
1. Вычисление искомой функции в подобластях, то есть решение приближенной задачи в подобластях с заданным значением v{n) на интерфейсе.
2. Расчет нормальных производных на сторонах подобластей, входящих в интерфейс. По окончании расчетов массивы производных пересылаются на процессоры-соседи, номера которых определяются до проведения итераций.
3. Вычисление разностей производных (5) на смежных сторонах подобластей. Перед проведением вычислений с каждого процессора-соседа читаются необходимые массивы производных.
4. Реализация очередного шага итерационного процесса по подобластям, то есть вычисление нового значения v{n+1). При этом могут потребоваться обмены информацией с процессорами-соседями, необходимой для реализации конкретного итерационного процесса, определяемого формулой (4).
3. Численные эксперименты
Рассмотренные алгоритмы и технологии были реализованы с использованием системы параллельного программирования MPI [7]. Расчеты проводились на кластере НКС-30Т Сибирского суперкомпьютерного центра СО РАН.
Цель численных экспериментов – исследование эффективности распараллеливания решения краевых задач на квазистуктурированных сетках. Наибольший интерес при этом представляют несогласованные сетки, так как одно из основных практических применений предлагаемого подхода – это решение задач с сильными неоднородностям на несогласованных сетках.
Рассматривалась модельная краевая задача для уравнения Лапласа: 'Au = 0 в G = {0.1 < x < 0.6,0 < у < 0.5} u г = f с точным решением и = 1 + lg д/x2 + у2 и значениями на границе f = и |г . Расчетная область покрывалась квазиструктурированной сеткой, которая представляла собой совокупность подсеток Ωh,k в подобластях Gk . Подсетки Ωh,k строились в шахматном порядке: соседние подобласти имели по каждому направлению число узлов, отличающееся в два раза, то есть были несогласованными. На рис. 2 приведен пример такой сетки, в которой число узлов макросетки равно Nx = Ny = 4 и число узлов подсеток - 8 х 8 , 16х16.
Рис. 2. Декомпозиция на 4 х 4 подобласти
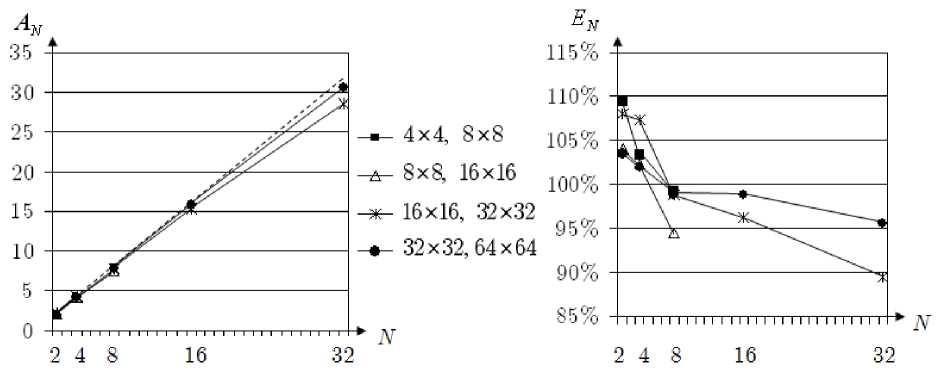
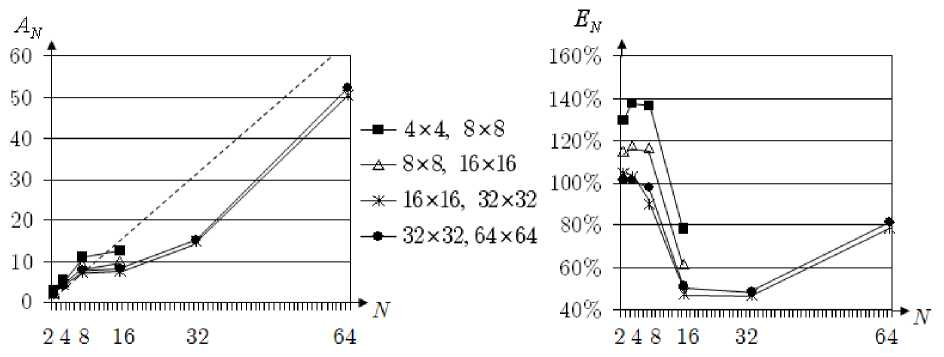
Подсетки группировались в объединения естественным образом: слева направо, снизу вверх в зависимости от числа процессоров N, на которых производится расчет. Все объединения имели одинаковое число узлов. Так, при N=2 в объединения включались подобласти, лежащие снизу-сверху от горизонтальной линии, при N=4 – снизу-сверху и слева-справа от горизонтальной и вертикальной средних линий и т.д. Расчеты проводились для числа подобластей N x х N y = 32 х 32, 64 х 64 и при числе процессоров N=2, 4, 8, 16, 32. Подсетки при этом имели следующее число узлов: Q hk = { 4 х 4,8 х 8 } , { 8 х 8,16 х 16 } { 16 х 16,32 х 32 } , { 32 х 32,64 х 64 } . Таким образом, самая густая ква-зиструктурированная сетка имела количество узлов, приблизительно равное ((32 х 32) х 32 + (64 х 64) х 32) х 64, что составляет более 10 миллионов узлов. Уравнение Лапласа аппроксимировалось обычной пятиточечной схемой. Производные, входящие в формулу (5), вычислялись по трехточечным схемам второго порядка. В качестве итерационного процесса брался метод сопряженных градиентов. Сначала были проведены численные эксперименты, которые показали, что относительная точность решения данной задачи составляет приемлемую величину порядка долей процента. Затем, для исследования эффективности распараллеливания проводилось заданное число итераций, равное 100.
Результаты экспериментов представлены на рис. 3, 4, где ускорение вычислений A N и эффективность процесса распараллеливания E N (последнее – в процентах) вычисляются по формулам
TA A N =T N , E N = N 100 , при различных вычислительных параметрах (пунктирной линией изображено линейное ускорение).
а) Ускорение A N
б) Эффективность E N
Рис. 3. Результаты для числа подобластей 32 х 32
а) Ускорение A N
б) Эффективность E N
Рис. 4. Результаты для числа подобластей 64 х 64
Из приведенных результатов можно сделать следующие выводы:
-
1. Ускорение вычислений A N растет с увеличением числа процессоров, что говорит о масштабируемости предлагаемого подхода.
-
2. Эффективность E N падает с увеличением числа процессоров, что объясняется увеличением числа межпроцессорных обменов.
-
3. При малом числе процессоров (не более 8) наблюдается явление сверхлинейного ускорения, при котором эффективность превышает 100 %, которое особенно заметно на сетках с большим числом подобластей, то есть при густой макросетке. Объяснение этому следующее. Подобласти группируются в объединения. Каждое объединение обрабатывается одним процессором. Расчет подобластей, входящих в объединение, на одном процессоре проводится последовательно, то есть одна подобласть рассчитывается автономно, что приводит к эффективному использованию сверхбыстрой кэш-памяти компьютера. Кроме того, малое число процессоров (или малое число объединений) говорит о малых затратах на обмены. Эти два эффекта: ускорение за счет кэш-памяти, с одной стороны, и уменьшение числа обменов, с другой стороны, – дают явление сверхлинейного ускорения.
Заключение
В работе рассматривался вопрос о распараллеливании решения двумерных краевых задач на предлагаемых квазиструктурированных сетках. Данные сетки просты в использовании и адаптивны к решению, которое ищется итерационным методом декомпозиции. Проведены численные эксперименты по распараллеливанию решения модельной краевой задачи на несогласованных сетках. Результаты численных экспериментов показали, во-первых, работоспособность и адекватность предлагаемого подхода, и, во-вторых, наличие сверхлинейного ускорения за счет влияния сверхбыстрой кэш-памяти. В дальнейшем планируется проведение исследований по эффективному использованию данного явления в предлагаемых алгоритмах и технологиях.
Список литературы О распараллеливании решения краевых задач на квазиструктурированных сетках
- Kuznetsov, Yu. Efficient iterative solvers for elliptic problems on nonmatching grids/Yu. Kuznetsov Yu.//Russian Journal of Numerical Analysis and Mathematical Modeling. -1995. -Vol. 10, No 3. -P. 187-211.
- Василевский, Ю.В. Методы решения краевых задач с использованием нестыкующихся сеток/Ю.В. Василевский//Труды Математического центра им. Н.И. Лобачевского. -Казань: УНИПРЕСС, 1999. -Т 2. -С. 94-121.
- Bernardi, C. A new nonconforming approach to domain decomposition: the mortar element method/C. Bernardi, Y. Maday, A. Patera//Nonlinear partial differential equations and their applications. -Paris: College de France Seminar, 1994. -Vol. 11. -P. 13-51.
- Свешников, В.М. Построение прямых и итерационных методов декомпозиции/В.М. Свешников//Сибирский журнал индустриальной математики. -2009. -Т. 12, № 3(39). -С. 99-109.
- Свешников, В.М., Построение квазиструктурированных локальномодифицированных сеток для решения задач сильноточной электроники/В.М. Свешников, Д.О. Беляев//Вестник ЮУрГУ, серия «Математическое моделирование и программирование». -2012. -Вып. 14. -№ 40(299). -С. 118-128.
- Ильин, В.П. Методы конечных разностей и конечных объемов для эллиптических уравнений/В.П. Ильин -Новосибирск: Изд-во ИВМиМГ (ВЦ) СО РАН, 2001. -318 с.
- Корнеев, В.Д. Параллельное программирование в MPI/В.Д. Корнеев -Новосибирск: Изд-во ИВМиМГ (ВЦ) СО РАН, 2002. -215 с.


