О равновесной концентрации вакансий в сплавах железа с водородом

Р.А. Рябов и П.В. Гельд [1] предложили теорию образования флокенов, в которой они рассматриваются как разросшиеся дискообразные скопления вакансий, возникающие благодаря конденсации неравновесных (избыточных) вакансий в условиях относительно быстрого охлаждения. Радиус диска может увеличиваться благодаря присоединению других вакансий. Начиная с какого-то момента водород испаряется внутрь диска, а его газ создаёт внутреннее давление, стимулирующее развитие флокена, ибо подвижность атомов водорода во много раз выше подвижности вакансий. Предложенный авторами [1] качественный механизм образования флокенов не противоречит известным в практике фактам.

Существование притяжения между вакансиями и атомами водорода отмечено в нескольких исследованиях [2–4]. Первопринципные расчёты [5, 6] также позволяют сделать вывод о сильном притяжении вакансий и атомов водорода в α -железе. Оказалось, что в одной вакансии могут накапливаться до шести атомов водорода [2, 5, 7]. Подобное взаимодействие приводит к росту концентрации вакансий, о чем свидетельствует ряд экспериментов [8, 9]. Поэтому возникает иная задача о влиянии взаимодействия водород–вакансия на равновесное количество вакансий и степень захвата вакансиями атомов водорода. Последнее может не стимулировать, а наоборот задерживать образование флокенов.

В данной работе представлены результаты расчётов «из первых принципов» энергии взаимодействия в комплексах вакансия–атом(ы) водорода и термодинамического моделирования температурной зависимости концентрации таких комплексов.

Первопринципные расчеты проводились методом линейных присоединенных плоских волн (LAPW) с учетом обобщенного градиентного приближения (GGA’96) в программном пакете WIEN-2k. В качестве модели для расчетов была выбрана суперячейка ОЦК-железа из 54 атомов, из которой удалялся 1 атом приблизительно в центре суперячейки. Все вычисления проводились с использованием 27 k-точек в неприводимой области зоны Бриллюэна. При этом радиус muffin-tin сферы Rmt был равен 2,0 а.е. и 0,7 а.е. для железа и водорода соответственно, параметр Kmax = 5,0; Ecut = 7,0 Рб.

На первом этапе была проведена релаксация атомов железа вокруг точечной вакансии, и для равновесного параметра решетки было получено значение a = 2,84 Å. Был проведён расчёт энергии образования вакансии для системы из N атомов в ячейке по следующей формуле:

EV ( N ) = E i ( N - 1,1, Q ) - NN- ■ E i ( N ,0, Q ), (1) где E 1 ( N , m , Q ) - энергия структуры, содержащей N атомов и m вакансий в равновесном объёме Q . При найденном равновесном значении постоянной решётки энергия образования вакансии б у = E ^f (54) = 2,15 эВ. Авторами [5] и [6] были получены значения соответственно e _V = 2,00 и 2,17 эВ.

Энергия захвата атома водорода в одиночную вакансию, содержащую n –1 атомов водорода с образованием комплекса V H n , определялась соотношением

E trap (1, n ) = E 2 (1, n - 1, Q ) + E 2 (0,1, Q ) - E 2 (1, n , Q ) - E 2 (0,0, Q ), (2) где E ₂(1, n , Q ) - энергия системы, состоящей из 53 атомов железа и n атомов водорода, находящихся внутри вакансии в равновесном положении с объемом Q ; E ₂(0,1, Q ) - энергия системы из 54 атомов железа и атома водорода в тетрапоре; E (0,0, Q ) - энергия системы из 54 атомов чистого железа при равновесном объеме Q .

Результаты расчётов в сравнении с данными работы [5] приведены в табл. 1. Видно, что они очень близки, поэтому найденные значения энергий E_trap (1, n ) , по-видимому, можно считать достаточно надёжными. Для n = 1 имеется также очень близкий результат [6]: E_trap (1,1) = 0,57 эВ. Экспериментальные оценки [2] дают усреднённые значения 0,63 эВ для n = 1...2 и 0,43 эВ для n = 3...6. В дальнейших расчётах будут использоваться найденные в нашей работе значения E trap (1, n ) для n = 1...4 и значения [5] для n = 5 и 6, которые нами не определялись.

Таблица 1

Энергии захвата атома водорода вакансионными комплексами E _trap (1, n )

Образующийся вакансионный комплекс	Etrap (1, n ), эВ
	Наши данные	Данные [5]
V H 1 ( n = 1)	0,603	0,56
V H 2 ( n = 2)	0,607	0,62
V H 3 ( n = 3)	0,396	0,40
V H 4 ( n = 4)	0,260	0,27
V H 5 ( n = 5)	–	0,33
V H ( n = 6)	–	–0,02

Общий подход к решению задачи о термодинамике твёрдых растворов внедрения, содержащих вакансии, был разработан А.А. Смирновым [10]; позже схожая теория была предложена авторами [11]. Однако указанные работы относятся к сплавам с ГЦК-решёткой; кроме того, некоторые использованные в них допущения не подтверждаются первопринципными расчётами, результаты которых представлены выше. Поэтому в данной работе проведено повторное рассмотрение задачи о равновесной концентрации вакансий.

Известно, что водород, растворяясь в ОЦК-железе, благодаря своему малому радиусу занимает тетраэдрические междоузлия в кристаллической решетке [5, 6, 12]. Рассмотрим твёрдый раствор внедрения водорода в решётке ОЦК-железа, содержащей вакансии, взаимодействующие с растворёнными атомами водорода. Будем считать, что атомы водорода занимают центры тетраэдрических пор, расположенных на гранях куба симметрично на расстоянии ¹ ₄ a от центра грани в количестве 4 поры на грань. Расстояние от центра тетраэдрической поры до центров ближай-

Мирзаев Д.А., Мирзоев А.А., Окишев К.Ю.,                 О равновесной концентрации вакансий

Шабуров А.Д., Рузанова Г.Е., Урсаева А.В.                          в сплавах железа с водородом ших атомов железа равно r1 = 45a a. Количество тетрапор, приходящихся в целом на один узел решётки, есть v = 6, но фактически каждый атом железа или вакансия окружены z2 = 24 тетраэдрическими порами, в которых могут находиться атомы водорода.

Таким образом, N _н атомов водорода размещены в v N тетрапорах, где общее число узлов N = N Fe + N V включает в себя N _Fe узлов, занятых атомами железа, и N_v вакантных узлов. Концентрацию атомов водорода 6 _Н будем выражать отношением

^ = N H .                               (3)

Для описания всевозможных конфигураций атомов водорода вокруг вакансий удобно ввести параметр nVl – число вакансий, имеющих в ближайшем соседстве l атомов водорода [10]. Если обозначить через £vH энергию связи атома водорода и вакансии, взятую с противоположным знаком, то для полной потенциальной энергии взаимодействия V–H во всей системе получается выражение z2

^£ v Н I n Vl l ,                                         ⁽⁴⁾

l = 0

к которому необходимо добавить энергию образования всех вакансий z2

^£ V I n vl = ^£ v^Nv ,                                   ⁽⁵⁾

l = 0

где г V - энергия образования моновакансии.

Однако приведённые выше результаты первопринципного компьютерного моделирования (см. табл. 1) свидетельствуют о том, что формула (4), предложенная в [10], неточна. При образовании комплекса vH 1 энергия системы изменяется на £ _{v Н1} = -0,6 эВ; присоединение следующего атома водорода (комплекс V H 2 ) уменьшает энергию ещё на 0,6 эВ. Но для третьего атома водорода понижение энергии составляет уже 0,4 эВ, для четвёртого и пятого ~0,3 эВ, а для шестого оно отсутствует.

В используемом приближении взаимодействия ближайших соседей конфигурационная энергия кристалла при 0Н «1 имеет вид z2

z ₂

E = E ^{0 (} ^ н ) ^{+ £} v E n vl ⁺ I ^£ v h l n vl .

l = 0 l = 0

Термодинамическая вероятность, или число различимых конфигураций взаимного расположения ближайших взаимодействующих соседей – атомов железа, водорода и вакансий при заданных N _Fe, N_V и всех n_Vl определяется выражением, приведённым в [10]:

Г      za.   I

^N Fe ⁺ I n vl ^!

W = ^У

l = 0

N Fe ! ∑ ^{z 2} n Vl

z 2 Г

z П l=0 У

n Vl

--z ²— I W ₂, l !( z 2 - 1 )! у

l = 0

где первый сомножитель отражает число микросостояний, возникающих при всевозможных размещениях по решётке вакансий, имеющих различное число ближайших соседей – атомов водорода, а

22.    ^

^W 2 ⁼ Г----

^N H ^-

У

iV NFe + I nvl _ У        l=0    у

z^

^z 2 1 n Vl Г !

22.     ^

22.    ^

I Invi !)V NFe + E %

l = 0      у

У        l = 0     у

l = 0

z ₂ z ₂ ∑ n_Vl l = 0

^2

Nн +1 lnvlV- l=0

представляет число способов размещения атомов водорода по тетрапорам с одинаковыми энергиями вдали от вакансий. Отрицательное слагаемое в числителе (8) возникает потому, что каждая вакансия, независимо от точного количества окружающих её атомов водорода, блокирует z ₂ тетрапор от заполнения их дополнительными атомами водорода. Второй сомножитель в формуле (7)

отражает различные конфигурации, которые могут возникать при размещении l атомов водорода в z2 тетрапорах внутри вакансии. Возможно, что не все из них являются стабильными, и действительное число возможных конфигураций атомов водорода меньше; но этот вопрос требует от- дельного исследования.

Поскольку конфигурационная свободная энергия

F = E - TS = E - kT ln W ,                             (9)

то для нахождения равновесного распределения атомов водорода по ближайшему окружению вакансий после подстановки соотношений (6), (7) и (8) в это выражение следует выполнить условие минимума свободной энергии как функции от n Vl :

^{∂ F} = 0 ( l = 0, 1, 2, 3, …).                                (10)

∂ n_Vl

После простых расчётов с использованием единственного допущения NH ≫ NV находим равновесные значения nVL = z2! . f NH ) . f 1N11 ) 2 exp f - EV + EV H l ) N l!(Z 2 -1)! (yNFe J ( VNFe J 4 kT /

Это выражение переходит в формулу (7) статьи [10], если принять ν = 1 , z ₂ = 6 и

εV H l = lεV H1 . Если взаимодействие вакансий с атомами водорода будет отсутствовать ( εVHl = 0 ), то согласно выражению (11) концентрация комплексов VHl будет соответствовать хаотическому распределению атомов водорода в железе с концентрацией вакансий:

Fe

nV      I E

^V = exp - ^V

N     ( kT

На основе полученной общей формулы запишем конкретные выражения для n Vl при различных l . В частности, доля вакантных узлов, в окружении которых нет ни одного атома водорода,

n V 0 ₌ N

f

(

-

NH I I E I

^H exp - ^V ;

6 N Fe J     ( kT J

(13 а )

поскольку NH ≪ NFe , то она практически совпадает с долей вакансий в чистом железе (12). Да- лее,

nV1 = 24 Nh ' 1 ⋅ 1- NH I 17 exp I _ Ey + Ey hi 1 , (13б) N ( 6 N Fe J ( 6 N Fe J kT J’ nV 2 = 276 r Nh I2 ⋅ f1 - NH I16     I J exp I _ EV + EVH2 1 . (13в) N ( 6 N Fe J ^3 ( 6NFe kT J’ nV3 = 2024 NH ⋅ 1 - N H 15 J exp r _ EV + EV H3 1 (13г) N ( 6 N Fe ( 6NFe ( kT J и т.д.

Выше в табл. 1 представлено изменение энергии связи при добавлении каждого следующего атома водорода к комплексу V H l –1 ; суммирование от 1 до l позволяет найти ε V H l :

l

ε _VHl = - ∑ E_trap (1, n ) ;                                     (14)

n = 1

рассчитанные значения ε _VHl приведены в табл. 2.

Для расчётов по формулам (13) требуется также энергия образования вакансии ε V . Следует отметить, что полученная из первопринципного расчёта величина ε _V = 2,15 эВ находится на верхнем пределе диапазона значений, наблюдавшихся экспериментально (от 1,4 ± 0,1 до 2,0 ± 0,2 эВ) [13, 14]. А. Зеегер в обзоре [15] на основании литературных данных и собственных экспериментов пришёл к значениям ε _V = 1, 61...1, 75 эВ, а из результатов работы [16], где непосредственно измерялась концентрация вакансий после закалки от 1040 К, получил ε _V = 1,59 эВ.

М.А. Штремель [17] считает наиболее надёжным значение ε _V = 1,6 эВ. Авторы [13] показали, что повышение концентрации углерода в α -железе с 2·10^–5 до 1·10^–3 мас. % приводит к снижению наблюдаемой энергии образования вакансии с 1,79 ± 0,10 до 1,53 … 1,60 эВ. Возможно, именно поэтому рассчитанное для чистого железа значение ε _V выше, чем в большинстве экспериментов. В дальнейших расчётах мы использовали экспериментальное значение ε _V = 1,6 эВ.

Таблица 2

Энергии захвата вакансией l атомов водорода ε V H l

l	0	1	2	3	4	5	6
ε VHl , эВ/вакансия	0	–0,603	–1,210	–1,606	–1,866	–2,196	–2,176

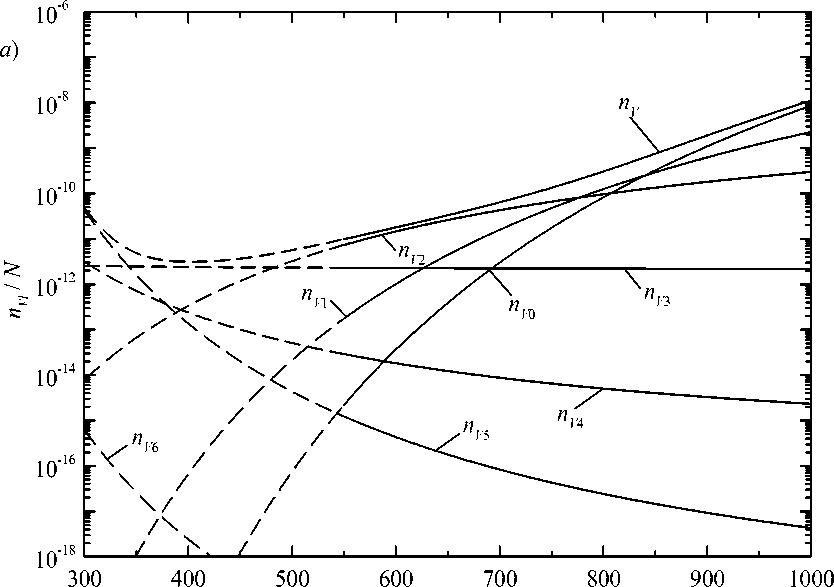
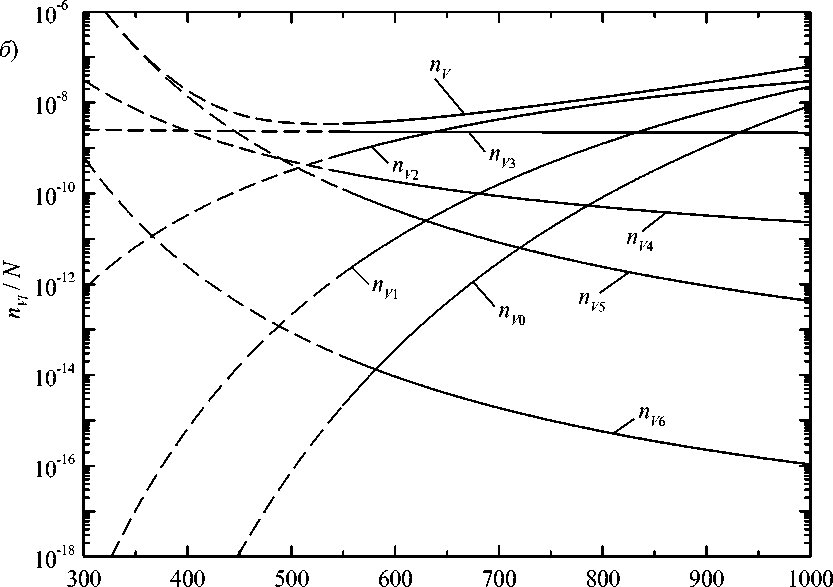
Результаты расчётов доли вакантных узлов, окружённых различным числом l атомов водорода, представлены на рисунке для концентраций водорода θH = 10-5 и 10-4 , что соответствует массовым концентрациям 1 и 11 ppm.

При всех температурах доля вакансий, содержащих 1, 2, 3 и более атомов водорода, значительно превышает долю одиночных вакансий, причём проявляется конкуренция между вакансиями с различным окружением. С понижением температуры преимущество последовательно получают комплексы V H 2 , V H 3 , а ниже 350 … 450 К почти все вакансии оказываются связанными с пятью атомами водорода ( V H 5 ).

Равновесное количество самих вакансий можно найти как сумму всех n Vl . При таком суммировании можно ограничиться l = 0…6, так как начиная с l = 6 энергия ε _{V H l} начинает уменьшаться

(табл. 2), что приводит к резкому уменьшению соответствующих n_Vl (см. рисунок):

n V ₌ ⁶ n Vl N  ^∑ l = 0 N .

Из графиков на рисунке видно, что взаимодействие с атомами водорода резко увеличивает равновесную концентрацию вакансий (напомним, что доля вакансий в железе, не содержащем водорода, практически совпадает с nV0 ). С понижением температуры этот эффект усиливается и N при 500 К может достигать 5…8 порядков. При более низких температурах значительной становится доля комплексов VH4 и VH5, для которых энергия взаимодействия εVHl превышает по абсолютной величине энергию образования вакансии εV и снижение концентрации вакансий должно смениться её ростом. Этот эффект резко усиливается с ростом общей концентрации водорода.

Впрочем, диффузия вакансий в железе ниже 500…600 К почти прекращается, поэтому указанные изменения равновесной концентрации вакансий при низких температурах в действительности могут не реализоваться. Это должно оказывать влияние и на эффекты захвата вакансиями водорода.

Таким образом, в данной работе предложен новый вариант статистической теории образования вакансий в сплавах Fe–H, учитывающий обнаруженный при первопринципных компьютерных расчётах эффект неодинаковой энергии связи с вакансией для различных групп атомов водорода, расположенных в первой координационной сфере, и показано, что, как и в теории А.А. Смирнова, взаимодействие с атомами водорода увеличивает равновесную концентрацию вакансий.

T , К

T , К

Температурная зависимость доли вакансий с различным окружением атомами водорода, рассчитанная по формулам (11), (13): а – при общей концентрации водорода θ H = 1·10^–5; б – при θ H = 1·10^–4