О разрешимости обратной задачи нахождения старшего коэффициента в уравнении составного типа

Пусть Q есть ограниченная область пространства Rⁿ с гладкой (для простоты — бесконечнодифференцируемой) границей Г, Q есть цилиндр Qx(0,T), 0<Т< +оо, Ь^у(ж, t), Ь^г(жД), г, з = 1, ..., п, b^x^tY К(ж), /(ж,#), и^х\ г<1(ж), ц(Ц — определенные при ж Е Q, t Е [О, Т] заданные функции, Ви — дифференциальный оператор, определенный равенством

Ви = b^x^Ux^ + b\x,t)uXi + b(x,t^u

(по повторяющимся индексам здесь и далее ведется суммирование в пределах от 1 до п). Обратная задача: найти функции u(x,t) и q(t), связанные в цилиндре Q уравнением q^utt - Aut -Ви = f(x, t),(1)

при выполнении для функции ц(ж, /) условий иСМ)1гх(о,т) = О,(2)

ц(ж,0) = г/о(ж), щ(ж, 0) = цЦж), ж Е Q,(3)

K(x)u(x,t) dx = ц(<), 0 < t < Т.(4)

В рассматриваемой обратной задаче условия (2) и (3) являются условиями обычной первой начально - краевой задачи для уравнения составного типа (1), условие же (4) есть условие переопределения интегрального вида, необходимое вследствие наличия дополнительной неизвестной (наряду с решением u(x,t^ функции q^t\ Подобные обратные задачи для уравнений составного типа (1) ранее не изучались.

Целью настоящей работы является доказательство разрешимости обратной задачи (1) - (4) в классе регулярных решений. Техника доказательства основана на переходе от исходной задачи к новой уже прямой начально - краевой задаче для нелинейного интегро -дифференциального уравнения составного типа вида (1), исследовании разрешимости новой задачи и далее построении с помощью решения новой задачи решения рассматриваемой обратной задачи. Близкая техника ранее использовалась автором в работах [1-3].

Перейдем к содержательной части работы.

Определим пространства V i и V 2"

У 1 = {«(ж, Z) : и(ж, t) € ioo(0, Т; ^(П) П W 2(^)), vt(x,t) Е Loo^T^^nW^^, nM €L2(0,T;ty^(Q))}, У2 = {«(жД): и(жД)еУ1, vtt(x,i) € L2(0,T; W22(n) ПЖ2(^))};

нормы в этих пространствах определим равенствами

^^1    ^'^^(О.Т^^ПЩ^П)) ⁺ H^ytILoo(0,T;W₂²(n)n]yi(n)) ⁺ 11^УИ^₂(0,Т;Ж1(П))’

ИУИу2 “ ^Иу! + ^“^ДО^И/Д^ЦПиД^))"

О о

Для функций и(жД) из пространств У i и У ₂ для почти всех t из отрезка [О, Г] выполняются неравенства

IM^IIl^q) < ^со521К(яД)||2₂(_П)< С1||^(жД)||^_2(п),              (5)

t

НМ1112(П)<2ТУ 1Мацт)||£2(п)^т + 2||у(ж,0)||£2(п)             (6)

о

— см. [4]. Далее, определим дифференциальный оператор By:

B1V = 6^(ж, f)v_XiX) + ЬДж, t>_Xi + Ь_#(ж, t>.

Предполагая, что коэффициенты операторов В и В^ ограничены, нетрудно показать, что для функций и(ж, t) из пространств У i и У ₂ для почти всех t из отрезка [О, Т] выполняются неравенства

П^(МН12(п) < МА«(жД)||£2(п),                     (7)

1|51у(жД)||^_2(п) < Ь₁||Ди(жД)||^_2(п),                            (8)

с некоторыми постоянными, определяющимися лишь функциями Ь^у(жД), У(жД) и Ь(жД), областью Q и числом Т.

Неравенства (5) - (8), а также собственно числа со, щ, 6q и bi нам понадобятся ниже.

Определим другие величины, которые понадобятся ниже. Пусть 70 и 71 есть заданные положительные постоянные (роль 70 и 71 будет прояснена ниже). Положим далее

F(t) = J K(x)f(x,t)dx,

/31 = max f 9 + ^ + ^lT2 + 2ЬоД >

2                 -470/

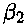
/ /1 ^x dt + 2 urai max[ f /²(жД) c/ж] + (biT + 2Z>o) [(Аио)²<3ж+ “ J              0

Q                                ft                                      ft

и

q

22 1^^^ JBu^t ¹⁼¹ n            q

М = 4Дехр(4АТ), 7V₂ = atm + A,

Q

N₃ = 2T² Ai + 2 у о

N₄ = I J K²^d \n

Теорема 1. Пусть выполняются условия

Wf + tMb)* •

b⁴^,^ ecHQY b\x,t) е c^Q), i,j = i,...,n, Цх^еС^У

К^ G C^Q);(9)

/(x,t)GL₂(Q), ftM Eb^QV uq^ g Ж²(П)ЛИ^(Л),

М^ЮФЖМ ^)6С-2([О,Т]);(10)

^"to>№>0,  F(t) >70+71, 70 >0,  71 >0, t€[O,T];(11)

j K^uo^ dx = д(0), J K^u^^x) dx = р'(ОУ,(12)

N4 < 71.(13)

Тогда обратная задача (1) - (4) имеет решение {u($,t),q(<)} такое, что u(x,t) G V i, ₉(t)GL₂([0,T]).

Доказательство. Воспользуемся комбинацией метода срезок, метода неподвижной точки и метода регуляризации.

Пусть N есть заданное положительное число. Определим функцию Gn(C) (срезку):

Gn^) =

-TV,

если если если

ki <  n, on, ^<-N.

Далее, для заданной функции и(жД) определим функции V’^,^у) ^и Ч^^У-

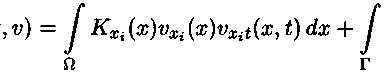
К(х)ихДх,^Угдз-

j\К(х)Ьг(х, <) — (K(x)bi3(х^^я^Ьх^х, <) dx — J K(x)b(x,t)v(x,t) dx+

J K^b^^x^^Uxi ^x,t^v₃ds г

(1/ = (i^i,..., i/n) — вектор внутренней нормали к Г),

Рассмотрим краевую задачу: найти функцию u(x,tY являющуюся в цилиндре Q решением уравнения

q(t, u)u_tt - Au_t - Ви = f^x, /)                            (Г)

и такую, что для нее выполняются условия (2) и (3). В данной краевой задаче уравнение (1') представляет собой нелинейное «нагруженное» [5, 6] уравнение составного типа. Разрешимость поставленной задачи докажем с помощью метода регуляризации и метода неподвижной точки.

Пусть е есть положительное число. Рассмотрим краевую задачу: найти функцию и(х, tY являющуюся в цилиндре Q решением уравнения

q(t, u^utt - E^u_tt - Ащ - Ви = f^x, t)                      (1')

и такую, что для нее выполняются условия (2) и (3). Наконец, пусть и(ж, <) есть заданная функция из пространства У 2- Рассмотрим краевую задачу: найти функцию u(x,tY являющуюся в цилиндре Q решением уравнения q^t, v^utt - eSutt - Дщ - Ви = f(x, t)                      (1')У)

и такую, что для нее выполняются условия (2) и (3).

Пусть выполняются условия (9) - (12) за исключением условия Д(ж, i) € L^QY Тогда, О как следует из [7], краевая задача (lg„), (2), (3) будет разрешима в пространстве У 2- Следовательно, при выполнении указанных выше условий данная краевая задача порождает оператор Ф, переводящий пространство У 2 в себя: Ф(и) = и. Докажем, что этот оператор О имеет в пространстве У 2 неподвижные точки.

Рассмотрим равенство

t

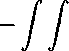
[^(т, и)и_ТТ — eAu_tt — Ди_т — Ви + и_т] Аи_тт dx dr.

о п

Интегрируя по частям и используя условия (2) и (3), нетрудно от данного равенства перейти к следующему

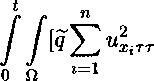
+ е(Дп_тт)²] dx dr +

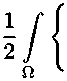
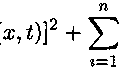
«^(^Д) ►

dx =

t

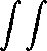
о Q

JAuTT dx dr —

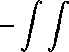
BuAuTT dx dr +

n (

s//

0 n

Ux^T^xiTT dx dr У

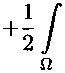
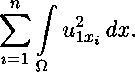
Положительность функции q(t, и), неравенство Юнга, неравенство (7) и лемма Гронуолла позволяют вывести из этого равенства априорную оценку

11(^итт)2 dxdr + j[Дц^(ж, t)]2 dx + У^ j и^.^х,^ dx < Со on              n              1=1 n с постоянной Со, определяющейся лишь нормами функции J^x,^ в пространстве ^(Q), функцией по (ж) и г<1(ж) в пространстве W§ (И) П W 2(H), числами Т и е. Из этой оценки, из неравенств (5) и (6) вытекает оценка

Ы« <  Сх                            (15)

V 2

с постоянной Ci, определяющейся теми же величинами, что и постоянная Со-

С помощью оценки (15) нетрудно установить, что оператор Ф, определенный выше, будет переводить некоторое замкнутое выпуклое ограниченное множество пространства V 2 в себя, и будет вполне непрерывным на пространстве V 2 — подробности рассуждений см. [1-3]. Согласно теореме Шаудера, оператор Ф имеет в пространстве У 2, по крайней мере, одну неподвижную точку и(х, t). Эта неподвижная точка даст решение краевой задачи (1'), (2), (3), принадлежащее пространству V 2.

Итак, краевая задача (1'), (2), (3) при фиксированном е имеет решение, принадлежащее пространству V 2; обозначим это решение и^е(ж,/). Покажем, что при выполнении всех условий теоремы 1 из семейства функций {u^£(®, i)} можно извлечь последовательность, сходящуюся к решению краевой задачи (I'), (2), (3).

В равенстве (14), соответствующем уравнению (1^.), выполним интегрирование по частям в первом и во втором слагаемом правой части. Получим равенство (индекс «е»у решения временно опустим)

J J V^L^tt + e^u^dx dx + - j        -V^-u^x,^dx =

0 Q 2=1                             П                 г=1

t

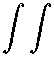
0 n

П

t

+ J J BvuAu_T dx dr — j on           n

П

П

П

t

+- JI BuTAuTdxdT+

0 n n *

j* J f^xiT^xiTT dx dx ^г=1 0 n

1 ' Г t^dx*-^ / ^iXidx.

Неравенство Юнга и положительность функции у(т, и) позволяют перейти от данного равенства к неравенству

— ^2 jJ ^их{тт dx dr + е J J (Д«_тт)² dx dr + ^ J^ut(x,t^² dx-V

2=1 0 n             on                n у J J к^тУ dx dr + ^ JI frdxdr+ on               1 0 n

n

• 2    /             «г J             - J J

П                 П               О П t                                     t                                       t

^^ JI^Ut^ dx dT + ^ J Jк^НтУ dx dx +-^ 11kB^2dxdx+

• ³    о n                 on                ⁴ о n

• ⁺ ^ /^^Ut^’ ^ ^{dx +} ~^ /V^Bukx, ^z)l^{2 dx}"^Tlj / ^uvr dx dx+ n                    ⁵ n                    ²⁼¹ о n

  ^V^J /"^&+ ly

  ^2—О П                П

  
  

  52 / ^^dx^ ²⁼¹ n

  
  

п            п

Используя далее неравенства (6) - (8), приходим к следующему неравенству

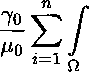
I [ △ щ(ж,4)]² dx+ n

• 1 Л Г ⁺ u_Xitkx,t)dx <

• ^£(—r^ ⁺ 2H ⁺ ~sr ⁺ li)j J^ ^M+

0 n tiA j^Ди^5 ^p dx + ^ J J j2dxdT + A_ j ^2^, c n                    1 О ПП

• + (^^- + ^) J к^иоУ dx + ^^f J ^uxiTT dx dr+ n                 ²⁼¹ 0 n

• ⁺ 2^52// ^ux_iT^dxdT + ^ jk^urydx+

• 6 2=1 0 nn

+^ 521 uixi dx-V I Buq^ui dx — J fkx, 0)Aui dx. 2=1 n          nn

Положим ^i = ^з = ^4 = 1, ^2 = 85 = |, <$6 = у 7о/^о ^Т- Учитывая введеные выше обозначения, получаем неравенство

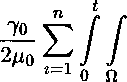
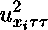
dx dr + г

t

11 (A«_TT)²

0 П

dxdr + - j [dut($,i)]²da:+ n

j n «                          Г Г               ⁷¹

+ 2 53 / ^((ж, ^^dx<01    [(A^r)² + 53 ^i^ ^{dx dT} + A-

¹⁼¹ a                on          «=1

Используя лемму Гронуолла, приходим к первой равномерной по е априорной оценке решений краевой задачи (1g), (2), (3):

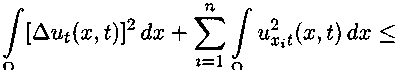
Из этой оценки очевидным образом выводятся следующие оценки t е J J"(Дитт)2 dx dr < N2, о п

J [Дгфж,^]² dx < W3. п

Кроме того, в целом из оценки (16) следует оценка

Мл < Nq V 1

с постоянной Nq, определяющейся лишь коэффициентами оператора В, функциями f(x,t), К^х\ p,(tY но(т), ^1(ж), областью Q и числом Т.

Оценки (18) и (20), теоремы о компактности вложений W^Q) С ^(Q), W2 (Q) ^с ^(Г) [8, 9], о возможности выбора из сильно сходящейся последовательности подпоследовательности, сходящейся почти всюду [9] и о слабой компактности ограниченного в L^ множества [10] дают существование функции н(ж,#), а также последовательностей {е_т} и {н_т(т,£)} таких, что при m —> 00

Em 0,

Um(^,t) -> Цх,^, Umx^X,t^ -7 их^Х^, Umt(x,t) -7 щ(т,£), итх^(х,£) —> uXit^x,t^ сильно в L2YQ) и почти всюду в Q,

Щпх^Х,^) ^ I^XiV^^Y ^mxitk^i^ ^ ^x^t СИЛЬНО в

L2 (Г х (0,7)) и почти всюду на Г х (0,7),

'^и-тХгХ₃ (ж, i) — V UxiXj^itY ^umxiXjt{^xit) ~^ ^uXiXjt>

Umtt^,^ -» Нн(ж,<) слабо в L₂(Q), E_mAu_mtt(x,t) -> о слабо в I^QY

Из данных сходимостей следует, что предельная функция и^х, /) принадлежит пространству V 1, является решением краевой задачи (I'), (2), (3), и что для нее сохраняются оценки (17), (19) и (20). Оценки (17) и (19) означают, в частности, что выполняется неравенство ;

|^(^“)| < N4.

Из этого неравенства и из условия (13) вытекает, что для решения н(ж,<) краевой задачи (I'), (2), (3) имеет место равенство

G71Wt,uY = ij)(t,uY

Положим,

Очевидно, что функции и(ж, t) и у(£) связаны в цилиндре Q уравнением (1). Умножим уравнение (1) с указанной выше функцией g(t) на функцию K^p’^t) и проинтегрируем по области Я. Полученное равенство и равенство (21) дают систему

q(t) j K(x)uu(x,t) -Vij)(t,u) = F(tY q(t)p"(t) + ^(t,u) = F(tY n

Из этой системы и вследствие положительности функции q(t) и условий согласования (12) вытекает, что выполняется равенство

У ^Г(ж)к(ж, f) dx = p(t).

Следовательно, для функции и(жД), являющейся решением краевой задачи (1'), (2), (3), выполняется условие переопределения (4).

Итак, построенные функции и(ж,<) и q(t^ связаны в цилиндре Q уравнением (1), для функции u(x,t) выполняются условия (2) - (4), функция u(x,t) принадлежит пространству V 1, функция q(f) — пространству ^^([О, Т]). Другими словами, построено требуемое решение рассматриваемой обратной задачи.

□

Пусть 7 есть заданное положительное число. Определим множество WY

Wi = {и(жД) : у(жД) € V 1, |^(^у)|<7 Vt€[O,T]}.

Теорема 2. Пусть выполняются условие (9), а также условия р'Ч^ > Мо > 0 при t Е [О, Т];(22)

f^x^EL^QY Mx,t)EL2lQY F^ >i>1 при £б[0,Т];(23)

К^ = 0 при х Е Г.(24)

Тогда обратная задача (1) - (4) не может иметь в множестве Wi более одного решения.

Доказательство. Предположим, что в множестве Wi имеется два решения {гц (ж, tY qi (<)} и {г/2(ж, tY 92^)} обратной задачи (1) - (4). Условие (22) позволяет дать предствление функций qi(t) и q₂(t^ через функции иДж,#) и ^(жД):

„ m F^“ ^и^ п F(t)-^Yu2)

Положим w(x, t) = г«1(ж,/) — u2(x,tY Имеют место равенство qi^uitt - Awt -Bw = [q2(t) - qi(t)]u2tt, (ж, t) E Q-,

ш(жД)|_Гх(_{0 Г}) = 0, w(x, 0) = wt(x,0) = 0, и E fl.

Следствием этих равенств является равенство

t j J qi^w^ 0 q

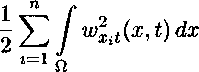
WXiWXjT

b4wZiTwIjT

dxdx+

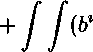
— Ьг^ )wXiwTT dx dx +

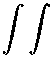
0 Q

dxdx +

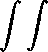
bwwTT dx dx+

t

^//^^      u_2ttw_tt dx dx.

0 Q

Используя условия (22) - (24) и применяя неравенство Юнга, а также первое неравенство (5) и неравенство (6), нетрудно от данного равенства перейти к неравенству

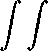
w^_T dx dx +

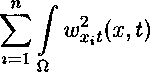
dx <

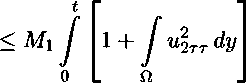
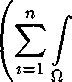
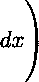
dx,

постоянная M\ в котором определяется лишь функциями /(ж, 4), А:(ж), /Д4), коэффициентами оператора В и областью Q. Из этого неравенства и из леммы Гронуолла вытекает, что функции w_Xit(x,t), г = 1. ..., п, шц(х,б) являются тождественно нулевыми в цилиндре Q функциями. Но тогда и функция w(x, t) будет тождественно нулевой в Q функцией. Другими словами, функции нДж, 4) и u₂(x,t) будут совпадать почти всюду в цилиндре Q. Из совпадения функций нДж, 4) и u₂(x,t) вытекает совпадение функций qi(t} и дДД- □

Определим множество И^:

W₂ = {и(ж,Д : и(жД) € У i, Дн(ДжД) G L₂(Q), |^(<,v)| < 7 V4 € [О,Г]}.

Теорема 3. Пусть выполняются условия (9), (22) и (23). Тогда обратная задача (1) - (4) не может иметь в множестве W₂ более одного решения.

Для доказательства этой теоремы достаточно уравнение для функции ш(ж, 4) умножить на Аш^ и проинтегрировать. Лемма Гронуолла вновь даст тождество w(x, 4) = 0. Из этого тождества и следует требуемое.

Сделаем несколько замечаний.

Аналогичные результаты о разрешимости обратной задачи нахождения решения н(жД) и коэффициента д(4) при второй производной по времени, о единственности решений можно получить при замене условия (2) на условие

(2')

9v 1гх(о,Т) -

Далее, изложенными выше методами можно исследовать разрешимость обратных задач нахождения решения н(ж, 4) и коэффициента при второй производной по времени с заданием на боковой границе цилиндра Q граничных условий первой или второй краевых задач в более общей ситуации — при замене оператора Лапласа произвольным линейным эллиптическим оператором, в случае функции К, зависящей не только от переменных дц, ..., жп, но и от переменной I.

Разрешимость вспомогательной линейной краевой задачи (1' Д, (2), (3) нетрудно установить непосредственно — например, с помощью метода Галеркина с выбором специального базиса.

Работа выполнена при поддержке Российского фонда фундаментальных исследований, код проекта N 06-01-00439, и Сибирского отделения РАН, интеграционный проект N 48.