О разрушении решения нелокального уравнения с градиентной нелинейностью

Прежде всего отметим, что значительный вклад в изучение линейных и нелинейных уравнений соболевского типа и, в частности, псевдопараболических уравнений внес выдающийся российский математик Георгий Анатольевич Свиридюк, например, в своих классических работах [1 – 4]. В этих работах были заложены базовые принципы нового и мощного метода полугрупп, который привел в дальнейшем к образованию одной из самых больших и широко известных в России научных школ, изучающих неклассические уравнения современной математической физики.

В данной работе мы рассмотрим начально-краевую задачу для следующего модельного уравнения:

t

∂

• — ( 4u — u ) + 4u + I ds h ( t — s ) 4u ( s ) + ^|Vu| ^p = 0 - ц >  0 , p >  0 , ∂t

а функция h ( t ) G C ⁽¹⁾ ([0 , + ro )) удовлетворяет следующим условиям:

max { h ⁽ t ) I, | h ' ⁽ t ) | 0 6 ^{X (} t ) ^- X ⁽ t ) 6 ^{0 -} X ⁽ t ) ^G C ^{(1) ([0} , + ^ro )) ,                (2)

причем функции x ( t ) , x ' ( t ) являются ограниченными постоянной h о >  0 .

В нашей предыдущей работе [5] мы рассмотрели соответствующее локальное уравнение

∂

dt (4u - u) + 4u + ^|Vu|p = 0, для которого мы рассмотрели начально-краевую задачу в ограниченной области с гладкой границей и получили результаты о глобальной во времени разрешимости и о разрушении его решения за конечное время. При этом мы рассмотрели случай, когда p G (0- NN—2 )

при N >  3 и p G (0 , + ro ) при N = 2 .

2.    Вывод уравнения

Рассмотрим область Q С RN при N ^ 2 с гладкой поверхностно-односвязной границей dQ G C ^{2 ,5} при 5 Е (0,1] в случае N ^ 3. Предположим, что эту область занимает кристаллический полупроводник. Как известно, в теории полупроводников (см., например, [6, 7]) хорошо работает квазистационарное приближение для системы уравнений Максвелла [8], электрическая часть которой имеет следующий вид:

div D = — 4nn, rot E = 0, D = E + 4n P ,                    (4)

где D — это вектор индукции электрического поля, E — это вектор напряженности электрического поля, P — это вектор поляризации среды, n — плотность свободных зарядов, причем в силу поверхностной-односвязности границы dQ определен потенциал электрического поля ϕ:

E = —V y.

Поскольку полупроводник, очевидно, является проводящей средой, то мы должны дополнить уравнения (4) уравнением для тока свободных зарядов, которое имеет следующий вид:

∂n

— = div J i + div J 2,                                (5)

∂t где J = Ji + J2 — это вектор тока свободных зарядов. Естественно, нам нужно записать выражение для этого вектора. При этом учтем тепловой разогрев полупроводника [9], тогда для вектора J1 имеет место следующее выражение [8]:

J i = a E - yVT, а > 0, y > 0,                          (6)

где T — это температура в полупроводнике, а величина J 2 учитывает временную дисперсию

t

J2(t) = У ds h(t — s)E(s).

Причем для температуры T имеет место уравнение теплопроводности с тепловым нагревом за счет электрического поля E следующего вида [9]:

_£— = A T + Q( | E | ),

где параметр £ > 0 имеет следующий вид [9]:

£ = £0e а и £о > 0 — это фиксированное число, а параметр а > 0 достаточно велик. Функция Q(|E|) описывает тепловую накачку в полупроводнике в самосогласованном электрическом поле E и хорошо аппроксимируется степенной функцией следующего вида [9]:

Q( | E | )= qo | E | ^p , p> 0,   qo > 0.

В силу свойства «малости» параметра (9) вместо уравнения (8) мы рассматриваем следующее уравнение:

A T + Q( | E | )=0.                               (11)

Теперь мы рассмотрим выражение для вектора P :

div P = poy,  po > 0,

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ что учитывает распределение связанных зарядов.

Дифференциальным следствием системы уравнений (4)–(12) является следующее уравнение:

t

∂

• — (Д у — 4проу) +   ds a(t, s) Д y(s) + 4п [a + a(0)] Д у — 4nYqo |V y | ^p = 0,     (13)

∂t которое элементарными заменами сводится к следующему уравнению типа С. Л. Соболева:

t

∂

— (Ду — у) + Ду + / ds h(t — s) Д y(s) + у |V y | ^p = 0, у > 0, p >  0. ∂t

В следующих параграфах мы будем рассматривать либо задачу Дирихле, либо задачу Неймана, поэтому обсудим физический смысл этих граничных условий. Действительно, однородное условие Дирихле y|дQ = 0

означает, что граница полупроводника «заземлена», а по договоренности электрический потенциал земли равен нулю. Однородное условие Неймана dnx Lq означает, что нормальная компонента электрического поля на границе полупроводника равна нулю.

3.    Задача Дирихле в Q C RN при N ^ 2

Прежде всего сформулируем классическую формулировку задачи, для которой мы дадим обобщенную постановку. Итак, пусть Q C RN при N >  3 является ограниченной областью с гладкой границей dQ G C ^{2 ,5} при 5 G (0,1].

t

∂

• —- (Д и — и) + Ди + dsh(t — s) Д u(s) + у |V u | ^p = 0 в QT, ∂t

и = 0 в Гт, и(х, 0) = uo(x) в Q,                         (16)

где Q t = (0, T) х Q, Гт = (0, T) х dQ. Мы будем рассматривать случай, когда p >  0.

Теперь сопоставим задаче (15)–(16) обобщенную постановку. Действительно, дадим определение.

Определение 1. Функция u(x)(t) класса

u(x)(t) G L^(0, T; H0(Q)), и ’ (x)(t) G L ² (0, T; H0(Q))

называется слабым обобщенным решением задачи (15)-(16), если при некотором T > 0 имеет место следующее равенство :

( D(u),w ( = 0 для п. вс. t G [0, T] и для всех w G H0(Q),

где (-, •) — это скобки двойственности между гильбертовыми пространствами H0(Q) и H-1 (Q), а t

D(u) = я" (Ди — и) + Ди + [ ds h(t — s) Дu(s) + y|Vu|p ∂t и uo(x) G Hq(^) П H2(Q).

Теперь мы рассмотрим различные случаи.

СЛУЧАЙ p G (0,1]. Сначала мы получим априорную оценку, из которой сразу же вытекает, что в данном случае нет разрушения сильного обобщенного решения. Действительно, возьмем в определении 2 слабого обобщенного решения функцию v(x)(t), равную решению u(x)(t), тогда после интегрирования по частям мы получим следующее равенство:

t

2 dt [ |V u » 2 + « и » ² ] + ||Vu « 2 + j dsh(t — s) j (Vu(s), V u(t)) dx = ^ j |V u | p udx.   (19)

0Ω    Ω

Поскольку при p G (0,1], очевидно, p ^ 1 + 2/N при N ^ 2, то в силу неравенства Гельдера и вложения

H q (Q) С Lq(Q) при q =----

2 — p справедлива следующая цепочка оценок:

/              \ p/2

(2-p)/2

^

^ У |V u | ^p udx <  | ^ | I У |V u | ² dx I

Ω

(p+1)/2

I г \

< ci(Q,p) | ^ | I / |V u | ² dx I ,

Ω где ci = ci(Q,p) — это соответствующая постоянная вложения (20). Таким образом, мы из (19) и (20) приходим к следующему неравенству:

2 d [ bv u h 2 + | u | 2] + bv u h 2 +

t ds

h(t — s) У

( V u(s), V u(t)) dx ^ c ₂ ||V u||p ⁺¹

Теперь мы воспользуемся неравенством Коши–Буняковского и получим, что имеет место неравенство

t

¹ 4 [ |V u | 2 + | u | 2] <  ¹ [ds | h(t - s)H |V u | 2(s) + th ⁰ |V u | 2 + C2 «V u » ?* ¹ .      (22)

2 dt                     2                               2

В силу арифметического неравенства Юнга при p G (0,1) мы приходим к следующему выражению

C2 »V u |P ⁺¹ <  G- p_C2 ^{/ (1- p )} + -2- |V u | 2.

Таким образом, отсюда и из (22) приходим при p G (0,1) к следующему неравенству:

t

¹ -d [ »V u « 2 + | u | 2] <  ¹ [ds | h(t - s) inV u « 2(s)+th ⁰ |V u fl 2+G - p_c2 ^{/ (1- p )} +^. ₈vu| 2 , (23)

2 dt                   2                          2           2

а при p = 1 мы сразу же имеем следующее неравенство:

t

1 -d [«Vu|2 + Bu|2] ^ 1 f ds |h(t - s)H|Vu|2(s) + th0 |Vu|2 + C2|Vu|2.(24)

2 dt                     22

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

Рассмотрим неравенство (23), т. е. случай p £ (0,1), поскольку при p = 1 все проще. Итак, после интегрирования по времени мы получим следующее неравенство:

t hVuhi C hVuohi + Wi + у j(t - s)hVuhi(s) ds+

t

+ (th° + p+1) /М2ds + Цг'А p't. (25) o

Пусть теперь t G [0, T] при некотором T > 0, тогда мы из (26) получим следующее неравен ство

t hVuhi C hVuohi + huohi + 1-pci/|1-P)T + (hoT + p+1) IhVuhi(s) ds,     (26)

o из которого в силу теоремы Гронуолла–Беллмана–Бихари мы получим следующее неравенство:

h V u h i(t) c

hVuohi + huohi +     ci/|1-p)T exp | (hoT + p+) )■ при t G [0, T].

Следовательно, норма Ц Vuhi(t) ограничена на всяком компакте из R^. Таким образом, сла- бое обобщенное решение рассматриваемой задачи не разрушается за конечное время. Докажем, что при uo(x) G Ho(^) П H2(Q) слабое обобщенное решение существует глобально во времени. С этой целью нам нужно воспользоваться классическим методом Галеркина в сочетании с методом компактности [10]. Таким образом, справедливо следующее утвержде- ние.

Теорема 1. Пусть p G (0,1] и uo(x) G Ho(^) П H ² (Q). Тогда существует слабое обобщенное решение задачи (15), (16) класса

u(x)(t) G L“(0, T; <(Q) П H2(Q)), u ‘ (x)(t) G L2(0, T; <(Q) П H ² (Q))

для произвольного T > 0.

СЛУЧАЙ 1 C p C 1 + 2/N. Докажем сначала теорему о локальной разрешимости задачи (15)–(16), понимаемой в слабом обобщенном смысле определения 1, в классе

u(x)(t) G C ⁽¹⁾ ([0,To); h o (Q))

при некотором максимальном To > 0, зависящем от uo(x) G Hj(Q). С этой целью рассмотрим следующий оператор:

Au = -Д и + I : Ho(Q) ^ H ^-1 (Q).

Используя теорему Браудера–Минти, и точно так же как и в работе [11], удается показать, что этот оператор обратим, причем обратный оператор является липшиц–непрерывным с постоянной Липшица равной 1. Тогда начально–краевую задачу (15)–(16), понимаемую в слабом смысле определения 1, можно представить в классе

u(x)(t) G C ⁽¹⁾ ([0, T]; <(Q))

в следующем абстрактном виде:

t у + B1A-1V + f dsB1A-1v(s) = ^|B2A-1v|p , v(0) = vo = A-1uo, v = A-1 u,    (29)

dt

o где

Bi = —△ : H0(Q) ^ H ^-1 (Q), B ₂ = V : H0(Q) ^ L ² (Q) 0 • • • 0 L ² (Q).

Заметим,

что оператор

B ₁ A ^-1 v : H ^-1 (Q) ^ H ^-1 (Q)

является венств:

липшиц–непрерывным. Действительно, имеет место следующая цепочка нера-

^|| B ₁ A ^-1 v ₁ — B ₁ A ^-1 v ₂^ ^ || A'

¹ v ₁ — A ¹ v ₂ | < ||v ₁ — v ₂ H * для всех v ₁ ,v ₂ Е H ¹ (fi). (32)

Докажем теперь ограниченную липшиц-непрерывность оператора |B ₂ A ¹ v|p. Действительно, имеет место следующая цепочка неравенств при q = 2/p и p Е [1, 2):

|| |B2A ^-1 V1| ^p — |B2A ^-1 V2| ^p | ^ ^

^ p || | V A ^-1 (V1) — V A ^-1 (v2)|max {| V A ^-1 (v1) |p ^-1 , | V A ^-1 (v2) |p ^-1 } | ^ ^

1/q

<

< С1(Р)(У | V A ^-1 (v1) — V A ^-1 (v2)|q x max { | V A ^-1 (v1) | ^{q ( p -1)} , | V A ^-1 (v2) | ^{q ( p -1)} } dx)

/                                           \ 1/2

< c ₁ (p) I У | V A ^-1 (v ₁ ) — V A ^-1 (v2)|2 dx I x

Ω

/                                                                                    \ (2-q)/(2q)

x I У max || V A ^-1 (v1) | ^{2( p -1) / (2- q )} , | V A ^-1 (v2) | ^{2( p -1) / (2- q )} } dx |

Ω

= ^(R) || V A ^-1 (vi) — V A ^-1 (v ₂ ) || ₂ ,

где

д(К) = ciR ^{p -1} , R = max { ||V A ^-1 (v1) || ₂ , || V A ^-1 (v ₂ ) || ₂} .

Заметим теперь, что в классе v(t) Е C(1)([0, T]; H-1(Q)) мы можем свести нашу задачу к интегральному уравнению ts

v(t) = v₀ + 1 dsG(v)(s), G(v)(s) = — B ₁ A ^-1 v(s) — У dah(s — a)B ₁ A ^-1 v(a) + ^ |B2A ^-1 v(s) | ^p .

^{0                                               0}                                             (34)

И при достаточно малом T > 0 в силу оценок (32) и (33) можно применить метод сжимающих отображений в банаховом пространстве

L“(0, T; H ^-1 (Q))

и доказать существование единственного решения интегрального уравнения (34) в этом банаховом пространстве. Далее можно воспользоваться «бутстэп» методом (см., например, [11]) и доказать, что это решение на самом деле из класса

C ⁽¹⁾ ([0, T]; H ^-1 (Q)).

Затем нужно применить стандартный алгоритм продолжения решений интегральных уравнений во времени и получить следующий результат.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

Теорема 2. Пусть p Е [1, 2) и uo(x) Е H0(Q), тогда найдется такое То = Tо(uо) > 0, что существует единственное решение u(x)(t) задачи (15), (16), понимаемое в слабом смысле определения 1 , в классе

u(x)(t) Е C(1)([0, То); H0(Q)), причем либо То = +го либо То < +го и в последнем случае имеет место следующее предельное равенство:

limsup|| V u|| ₂ (t) = + го .                                   (35)

t↑T 0

Очевидно, что это решение, вообще говоря, не единственное.

СЛУЧАЙ p Е (1 + 2/N, N/(N - 2)) при N >  3 или p > 2 при N = 2.

Дадим определение.

Определение 2. Функция u(x)(t) класса

u(x)(t) Е L“(0, Т; H0(Q) П H2(Q)), u ‘ (x)(t) Е L2(0, Т; H0(Q) П H ² (Q))        (36)

называется слабым обобщенным решением задачи (15)-(16), если при некотором T >  0 имеет место следующее равенство :

( D(u),w ) = 0 для п. вс. t Е [0, Т], и для всех w Е H0(Q),            (37)

где {•, •) — это скобки двойственности между гильбертовыми пространствами H0(Q) и

H-1 (q), а t

D(u) =    ( △ u — u) + △ u + ddh h(t — s) A u(s) + AVu | ^p ,

∂t uo(x) Е H0(Q) П H2(Q).

Докажем, что при uo(x) Е H0(Q) П H ² (Q) слабое обобщенное решение существует локально во времени. С этой целью нам нужно воспользоваться классическим методом Галеркина в сочетании с методом компактности [10].

Таким образом, справедливо следующее утверждение.

Теорема 3. Пусть p Е (1 + N2, AN-2) при N ^ 3 или p > 2 при N = 2 и uo(x) Е H0(Q)ПH2(Q). Тогда существует единственное слабое обобщенное решение задачи (15), (16) класса u(x)(t) Е L“(0, Т; H0(Q) ПH2(Q)), u (x)(t) Е L2(0, Т; H0(Q) ПH2(Q)) для некоторого малого Т > 0.

4. Разрушение решения

Прежде чем переходить к получению достаточных условий разрушения, нам нужно изучить сходимость следующего интеграла — нелинейную «емкость»:

a(p; Q; N )

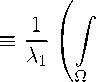
|V ^ ₁ | ^{p/ ( p -1)} ^1 ^{/ ( p -1)} (x)

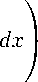
(p-1)/p

где функция ^1(x) — есть первая собственная функция, соответствующая первому собственному значению А1 > 0 оператора Лапласа в ограниченной области Q С RN с гладкой границей dQ Е C ^2,5 при 5 Е (0,1]:

△ ^1(x) + А1 ^1(x) = 0, ^1(x)|d = 0.

Обозначим через ро = ро(^; N ) > 1 такое число, что при р > ро интеграл в правой части равенства (38) сходится. Докажем, что существуют области Q С RN, для которых такое ро существует. Действительно, пусть Q = B r = {x G RN : | x | < R} — шар радиуса R> 0. Тогда можно вычислить первую собственную функцию и первое собственное значение задачи (39) (см., например, [12]). Действительно,

^1(x) = ^1(Ы) = cor(2-N )/2J(N-2)/2 (A1/2r), A1 = (zR 2) , r = |x|, где zni — первый корень функции Бесселя J(n2)/2(x). Заметим теперь, что для функции Бесселя Jv (z) справедлива следующая формула Эйлера [13]:

J v (z) =

(2 z) ^v r(v + 1)

+“       2

П 1 - n=1 1     zv'n)

где z_v,1 < z_v,2 <  • • • <  z _v,n <  • • • — это корни функции Бесселя J _v (z). Из явного вида (40) следует, что подынтегральная функция в (38) имеет интегрируемую особенность при р >  2, т. е. число ро = 2 в случае шара. Теперь мы предположим, что рассматриваем область Q, для которой число ро существует, и пусть

Р > Ро.

Получим достаточные условия разрушения слабого обобщенного решения задачи (15)–(16) при таких р. С этой целью возьмем в качестве w = ^1 (x) G Н0(^) П H ² (Q) в равенстве (37), тогда после «интегрирования по частям» получим следующее равенство:

t

(A1 + 1),, + A1J(t) + А1 / dt

ds h(t — s)J(s)

о

= E

j |V u | ^p^(x) Q

dx,

J(t) '

Q

u(x)(t)^1(x).

Справедлива следующая цепочка выражений:

| J | = У u^1(x) dx = a“ У u^E dx =

Q

Q

—   ( V u, V ^1) dx ^

^A1 J

Q

<     [ |V u ||V ^1 | dx = ^ [ ^ ^1/P IVU m l

A1                    A1

QQ

< -1 ([ ^|VN ^{p/ ( p -1)} _d Vp^{-1) /P} [ r_{pиП1 d ж} |

" A1 U ^ ¹ /(P- ¹ )(x) dx)        \J |   | ^1 dx)

IV^ dx < ^1 ^/p

1 /p

.

Таким образом, из неравенств (42) и (43) приходим к следующему обыкновенному интегро– дифференциальному неравенству:

t

(A1 + 1)^7 + A1J(t) + A1 [ dt

о

dsh(t — s)J(s) ^ E | J(t) | ^p ,

J(t) v

Q

u(x)(t)^1(x),

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ из которого с учетом условий (2) сразу же получаем неравенство

t dsX(t - s)J(s) » -g-|J(t)r

^{( A}i + 1)-у- + ^AiJ(t) + Ai ( dt

Заметим, что J(t) G C(1)([0, T]), поэтому справедлива формула интегрирования по частям tt

/^{dsx ( t} - ^{s )J} (^{s )} = ^- 0 Mt - _№

-

t

x(t - s)J(s)|    + [ dsx(t - s)J‘ (s) = s=0

t

= ^- X ^{(0)J( t ) +} X ^{( t )J(0) +} j ^dsX ^{( t} - ^{s )J} ‘ ^{( s )} - ⁽⁴⁶⁾

С учетом условий (2) мы имеем x(t) <  0, поэтому с учетом неравенств (46) мы приходим из (45) к следующему неравенству

t

(Ai + 1)dJ + Ai (1 + ho) J(t) >     | J(t) l p — [ dsx(t — s)J ‘ (s), J(t) = / u(x)(t)^i(x).   (47)

dt                      a ^p

Ω

Предположим теперь, что имеет место начальное условие

Jo =

j uo(x)^ _i (x) dx >

Ω

( A i(1 + ho)a ^p y^{/ ( p -i)}

но тогда из неравенства (45) вытекает, что имеет место неравенство dJ dt(0) > 0.

Таким образом, найдется такое ti G (0, T], что dt (t) > 0 при t G [0, ti].

Следовательно, из (45), (46) и (50) мы приходим к следующему неравенству:

^{( A}i ^{+ 1)}”T7 ^{+ A}i ^{(1 + h}0 ^{)J( t )} ^ ” | ^{J( t ) | p} при t ^{G [0 ,} ti]-dt                     a ^p

Таким образом, доказано следующее утверждение.

Теорема 4. Пусть p > p0 . Тогда при выполнении условия

Jo > ( A id 4_iho)a^p ) ^{i / (p}-¹⁾ _

Jo = У uo(x)^ _i (x) dx

Ω

имеет место предельное равенство

limsup J(t) = + ro , T^ <

tTT^                        P - 1

in (1 - AillG-NG j _o-p) ,

где

J(t) x/ Ω

u(x)(t)^ _i (x) dx.

и значит решение задачи (15), (16), понимаемое в слабом обобщенном смысле определения 1, разрушается за конечное время.