О развитии некоторых направлений конструктивной геометрии

Исторически сложилось так, что в математических науках – носителях фундаментальных знаний – не использовался их идейно-нравственный потенциал, богатое гуманитарное и культурное содержание. Каждый человек, желая уяснить смысл науки, обращается к ее истории. Наш соотечественник А.К. Рерих писал: "Камни прошлого – это ступени, ведущие к будущему", а великий Г.В. Лейбниц предостерегал о том, что тот, кто хочет ограничиться настоящим без знания прошлого, никогда его не поймет.

Изучение истории математики имеет большую общекультурную значимость и мировоззренческую направленность ввиду того, что первоначальные математические факты всегда были неотделимы от практических потребностей человека. Она обусловлена тем, что математические понятия и методы следует рассматривать не как застывшие раз и навсегда данные, а как развивающиеся и изменяющиеся под воздействием и влиянием развития общества.

Одни и те же теории, созданные независимо друг от друга, свидетельствуют об объективном характере развития математики,

благодаря которому совершаются открытия. Задачи Древней Греции, стран Востока, Европы демонстрируют связь математических знаний с культурными традициями общества, являются источником получения сведений межпредметного характера.

Отражение истории науки существенно, так как в ней показано развитие идей и методов, за которыми стоит множество как знаменитых, так и безвестных ученых. Элементы истории математики являются связующим звеном математики с другими дисциплинами.

На любом из этапов развития человечеству было свойственно стремление к прекрасному, возвышенному. История математики хранит немало сведений, достойных восхищения и эстетического наслаждения, позволяет расширить чувственный мир человека, сделать более наглядными те математические факты, о которых идет речь. Отмеченное выше в полной мере относится и к геометрии. На протяжении многих веков она служила образцом математической строгости. Геометрические построения были орудием исследований. Лучшие умы человечества более двух тысяч лет осуществляли поиск решения классических задач древности, формировали теории и законы.

Построения циркулем и линейкой, знакомство с происхождением геометрических терминов и формированием понятий; выра- ботка подходов к решению задач представляют научный, практический, методологический и исторический интерес.

Одним из важных разделов элементарной геометрии является материал, связанный с многоугольниками, многими касающимися их проблемами, историческими фактами, персоналиями.

В статье представлен конкретный исторический материал, относящийся к использованию учеными разных времен и государств циркуля и линейки при решении различных видов геометрических задач.

Уже в древних египетских и вавилонских памятниках встречаются правильные 3-, 4-, и 8-угольники в виде изображений на стенах и украшениях из камня. Древнегреческие ученые проявляли большой интерес к правильным многоугольникам еще со времен Пифагора Самосского (VI в. до н.э.). Ему приписывается систематическое введение доказательства в геометрию. В пифагорейской гетерии умели строить правильные 3-, 4-, 6-, 8-угольники. В связи с исследованиями они доказали теорему о том, что плоскость вокруг точки можно заполнить только тремя видами правильных многоугольников: треугольниками, квадратами и шестиугольниками (рис.1, а-в ). Они, как видим, стояли у истоков теории пакетирования и упаковок, столь актуальной в наши дни.

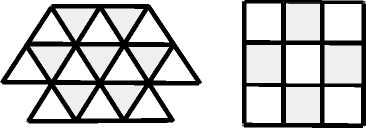
а )                     б )

в )

Рис. 1

В школе Пифагора классическими средствами были впервые построены правильные вписанные в окружность выпуклый (пентагон) и звездчатый (пентаграмма) пятиугольники, изображенные на рис. 2. Диагонали пентагона, образующие пентаграмму, делятся в среднем и крайнем отношении:

(a - x) : x = x : a, как впервые доказали пифагорейцы.

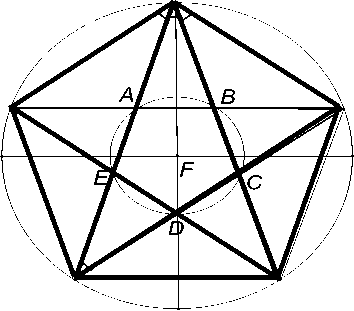
Рис. 2

Отсюда х2 = а(а - х) и x = —— , где а - длина диагонали, а х - ее большая часть [1].

Ниже проведено построение (рис. 3):

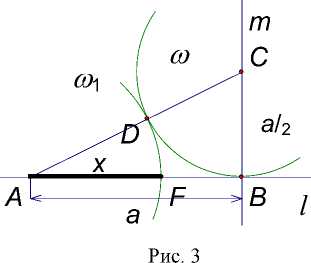
• 1.    l ;

• 2.    AB : AB = a , AB c l ;

• 3.    m : m ± l , B e m ;

• 4.    BC : | BC| = ^a / 2 , C e m ;

• 5.    AC ;

• 6.    a ( C ; a / 2 );

• 7.   a 1 ( A ; AD );

• 8.    D : D = AC na , D e AC ;

• 9.    F : F = AB no 1 , F e AB ; AF - искомый отрезок x .

Это уравнение в школе Пифагора решалось эллиптическим способом приложения площадей. Впоследствии такое деление отрезка великий художник и изобретатель Леонардо да Винчи (1452-1519) назвал "золотым сечением".

В разработку методов решения задач на построение существенный вклад внес Платон (428-342 до н.э.). Он считал задачу геометрической, если при ее решении использовались циркуль и линейка, т.е. классические инструменты. В противном случае она таковой не являлась. И в наши дни задачи на построение решаются так, как это было в Академии Платона, по четырем этапам.

Учение о правильных многоугольниках было продолжено и систематизировано в IV книге "Начал" Евклида (365-ок. 300 до н.э.). Он поместил в ней построенные классическими инструментами квадрат, правильные 5-, 6- и 15 - угольники. Доказана также формула удвоения числа сторон правильных вписанных многоугольников. Таким образом, древние греки умели строить многоугольники при n равном 3 • 2 k , 4 • 2 ^к , 5 • 2 k , 15 • 2 ^к , где k e N _o. Открытым оставался вопрос о возможности построения циркулем и линейкой правильных n -угольников: 7, 9, 11, 13, 14, 18, 22,

Правильные многоугольники нашли широкое практическое применение в античной архитектуре, астрономии, ювелирном деле и изобразительном искусстве. Древнеримский архитектор М.Н. Витрувий (I в. до н.э.) в "Десяти книгах о зодчестве" описал правила построения правильных 8- и 16-угольников в связи с планировкой городов, строительством крепостей и устройством солнечных часов [2]. В разделе, посвящённом планировке древнегреческих городов, требовалось спланировать улицы таким образом, чтобы на них не дули основные ветры. При этом предполагалось, что таких ветров восемь, и дуют они в определённых направлениях. Если около центра города провести окружность, то они совпадают с радиусами, проведёнными из центра в вершины правильного восьмиугольника. Считалось также, что имеется ещё 8 второстепенных ветров. Следовательно, для учёта и их воздействия следует построить правильный вписанный 16-угольник и расположить улицы города под определённым углом по отношению к диаметрам, соединяющим соответствующие вершины [3, с.18].

Древнегреческий астроном, математик и географ Клавдий Птолемей (II в.) в "Альмагесте" вычислил длины сторон правильных вписанных 3-, 4-, 5-, 6- и 10-угольников.

Много веков спустя в построение правильных многоугольников внес вклад и 20-летний Карл Фридрих Гаусс (1777-1855). Ему удалось доказать критерий возможности построения классическими средствами в том и только том случае, когда число n может быть представлено в виде: n = 2 mpi p 2.ps, где тeN0, a p 1, p2, ..., ps - простые числа вида 22 +1, где ke N0. В честь этого замечательного открытия памятник Гауссу в Брауншвейге стоит на 17-угольном постаменте.

Из критерия Гаусса следовала принци- пиальная возможность построения классическими средствами правильных многоугольников при п = 257 и п = 65537, т. е. имеющих вид 22 +1, когда к равно 3, 4 соответственно. Сколько же терпения и мужества потребовалось для их построения французскому математику Ф. Дж. Ришело (1808-1875) и немецкому ученому О. Гермесу (1826-1909)! Их изложения построения заняли 80 страниц у первого и целый чемодан рукописей у второго ученого.

В XIX в. теорию многоугольников развивали А.Ф. Мёбиус (1790-1868), К.Г.С. фон Штаудт (1798-1867), К.Ф.А. Якоби (1795-1855), Я. Штейнер (1796-1863) и другие. Благодаря им было показано, что задача деления окружности на n равных частей решается классическими средствами тогда и только тогда, когда уравнение деления круга (окружности) решается в квадратных радикалах.

Новое направление в решение геометрических задач с помощью циркуля и линейки внесли Георг Мор (1640–1697), которого называли "датским Евклидом", и итальянский геометр Лоренцо Маскерони (1750–1800). Независимо друг от друга они пришли к выводу о том, что всякая геометрическая задача на построение фигуры, состоящей из конечного числа точек, разрешимая циркулем и линейкой, может быть решена только циркулем. Вслед за ними французский математик и инженер Ж.В. Понселе (1788–1867) и швейцарский геометр Я. Штейнер доказали, что в условиях предыдущей проблемы задача, решаемая классическими средствами, может быть решена одной линейкой, если на плоскости построена какая-либо окружность с отмеченным центром.

Древнегреческое предание повествует о том, что на эллинской земле умельцы создали чудесный золотой сосуд, состоявший из чаши и подставки. Впоследствии крестоносцы доставили его из Византии для средневековых западноевропейских архитекторов и золотых дел мастеров. Схематичный рисунок этой чаши можно получить, если в правильном пятиугольнике ABCDE провести три диагонали: BE, BD, EC (рис. 4) [4]. Замкнутая линия BECDB представляет профиль изделия. Зако- ном этой "золотой чаши" является равенство

BE BK отношений    =

DC KD

MK

KN ^.

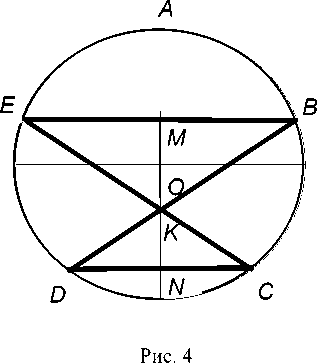
Для русского средневекового зодчества характерно изображение шлемовидного купола – элемента зданий, церквей и других культовых сооружений. В наставлении для мастеровых указывалось, как определить периметр и поверхность для покрытия купола золотом по заданному диаметру и дополнительному условию: треугольник ABC – правильный (рис. 5).

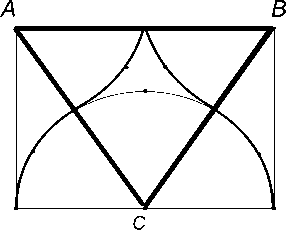
Рис. 5

сти и по длине его стороны. Первый был разработан ещё в Древней Греции, а второй – учёными стран ислама.

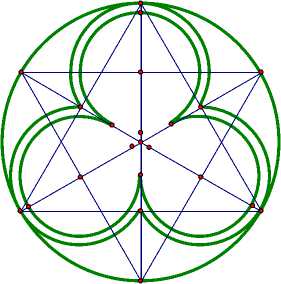
Рис. 6

Свойства правильных вписанных треугольников и шестиугольников (рис. 7) пользовал ещё Гиппократ Хиосский (V в. до н.э.) при своём решении знаменитой задачи о квадратуре круга . Впоследствии он занялся исследованием проблемы квадрируемых гур, носящих его имя ( луночки Гиппократа ).

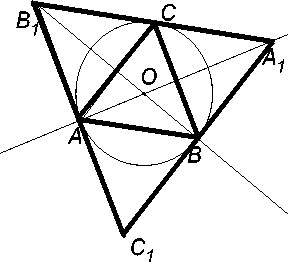
Рис. 7

К сложным геометрическим задачам, с которыми сталкивались строители средневековой Западной Европы относилось проектирование входных дверей и окон. Они обычно имели сложный орнамент из рам [5], имевший вид либо правильного многоугольника с дуговыми сторонами, либо более сложной фигуры, основанной на таком многоугольнике (рис. 6).

Построение правильных многоугольников

Исторически сложилось так, что при построении правильных многоугольников наметились два пути: вычисление длины стороны a n через радиус R описанной окружно-

Построение правильного вписанного в окружность шестиугольника с исчерпывающим доказательством дано в " Началах " Евклида. Очевидно, вершины, соединённые хордами через одну, образуют правильный треугольник (рис. 8). Такой шестиугольник всегда привлекал внимание в теоретических разработках и практических руководствах учёных благодаря простоте построения и интересным свойствам. К ним, в частности, относится тот факт, что квадрат его меньшей диагонали в три раза больше квадрата стороны …

В эпоху Возрождения учёные заметили, что фигуры в виде правильного шестиугольника встречаются в природе. Л.Б. Альберти

(1404–1472) писал о том, что " … природу радует шестиугольник …, а потому пчёлы и все другие насекомые умеют строить только шестиугольные ячейки в своих сотах " [6, с. 217].

За-построе-правиль-шести-угольни-Дюрер (1471– считал более кой ввитого, что мож-

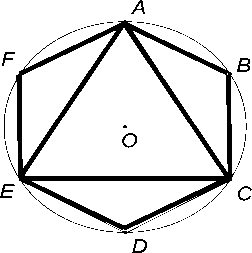
дачу ния ного ка А.

1529) наи-лёг- ду его

Рис. 8               но по-

стро- ить циркулем постоянного раствора. Такой шестиугольник стал объектом исследований И. Кеплера (1671–1630). Рассуждая о том, почему снежинки имеют такую форму, он отметил ряд свойств 6-угольника: плоскость можно построить без зазоров и наложений лишь равносторонними треугольниками, квадратами и правильными шестиугольниками. При этом среди них лишь правильный шестиугольник покрывает наибольшую площадь. Далее, из всех правильных фигур шестиугольник – это первая, из которых нельзя составить объёмное тело [7, с. 5–32].

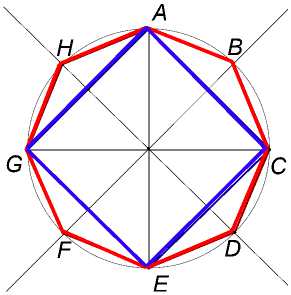
Рис. 9

В трактате "Стереометрия винных бочек" [8] И. Кеплер ссылается на Архимеда (287–212 до н.э.), показавшего, что отношение длины окружности к диаметру заключено в пределах 310 < п < 3! , и доказал этот факт. С 71         7, этой целью ученый использовал различные фигуры, вписанные или описанные около круга [8, с. 111–114]. Кеплер же в качестве такой фигуры взял правильный шестиугольник.

Проблема построения правильных вписанных четырёхугольников и восьмиугольников также имела важное научное и практическое значение (рис. 9). Они встречаются ещё в вавилонских текстах [9]. Построение квадрата осуществлялось следующим образом: проводилась окружность, а в ней – два взаимно перпендикулярных диаметра, четыре точки пересечения которых с окружностью являлись вершинами квадрата. Впоследствии все авторы строили правильные вписанные 4- и 8- угольники таким способом.

Построение правильных 5- и 10 -угольника занимало особое место, начиная с древних греков. Правильный пятиугольник часто встречается в природе: такую форму имеют очертания минералов, цветов, плодов, некоторых морских животных и т.д. В древности его изображению придавали мистическое значение. Знáком принадлежности к пифагорейской гетерии считали пентаграмму, образованной диагоналями пентагона (рис. 2). И пентагон, и пентаграмма как составные части входили в орнаменты, которые широко использовались в архитектуре, живописи, а также в произведениях мастеров-ювелиров, гончаров.

В 10-м предложении своей XIII книги Евклид доказал теорему о том, что квадрат стороны правильного вписанного 5-угольника равен сумме квадратов, вписанных в тот же круг правильных 6-угольника и 10-угольника [10]. Эта и другие теоремы были вспомогательными для доказательства следующих за ними теорем о пяти видах правильных выпуклых многогранников .

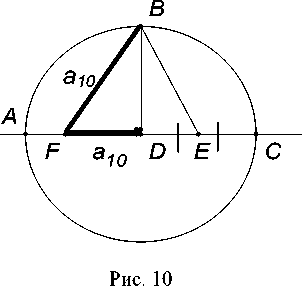
Десятую главу I книги " Альмагеста " Птолемей начал с построения правильных 5-и 10-угольников. Он рассмотрел окружность с центром в точке D и диаметром AC (рис. 10). В точке D восстанавливал перпендикуляр к AC , пересекающий окружность в точке B .

Проводилась окружность ω ( E , BE ) пересекающая AC в точке F . Тогда BF=a 5 . Заметим, что еще в IV в. до н.э. Менелай доказал, что FD является стороной правильного вписанного десятиугольника (рис. 11). Этому факту учёный дал чёткое доказательство, основанное на делении отрезка в отношении " золотого сечения " .

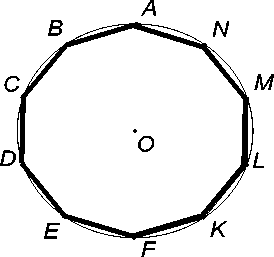
Рис. 11

Методами построения правильных пятиугольников интересовался А. Дюрер не только как учёный и художник, часто обращавшийся к орнаменту. Решая вопросы фортификации, он обратил внимание на то, что план крепостных сооружений часто имел форму пентагона [11]. В своём труде " Руководство к измерению с помощью циркуля и линейки в линиях, плоскостях и целых телах, составленное Альбрехтом Дюрером и напечатанное с соответствующими чертежами в 1525 г. на пользу всем, любящим искусство " [12] ученый предложил два способа построения правильного 5-угольника – точный и приближённый.

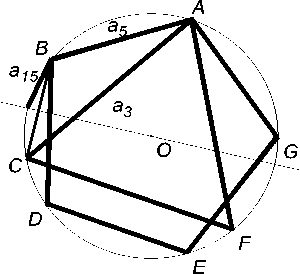
Рис. 12

В IV книге "Начал" Евклида впервые был указан способ построения правильного 15-угольника. Ученый заметил, что дуга на- клонения эклиптики к экватору представляет 1/15 часть всей окружности, т.е. стягивается стороной правильного вписанного 15-угольника. Но 2/15 = 1/3 – 1/5, поэтому 1/15 часть окружности находится как половина разности длин дуг, стягиваемых сторонами правильных 3- и 5-угольников (рис. 12).

Заключение

Таким образом, в статье представлен конкретный историко-математический материал, касающийся методов построения выпуклых вписанных и описанных многоугольников с помощью циркуля и линейки ученых разных времен и народов. Указаны различные методы построения таких фигур, описаны приложения многоугольников в пакетировании, зодчестве, архитектуре. Исторический интерес представляет также разработка методов их построения по данной стороне. Кроме того, так как ученые стран ислама пользовались линейкой и циркулем постоянного раствора, то хотелось бы осветить точные и приближенные методы построения таких многоугольников с использованием указанных инструментов. Однако эти вопросы представляют материал другой статьи.