О развитии второго метода Ляпунова качественного исследования в целом динамических систем



Качественная теория

ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

О РАЗВИТИИ ВТОРОГО МЕТОДА ЛЯПУНОВА КАЧЕСТВЕННОГО ИССЛЕДОВАНИЯ В ЦЕЛОМ ДИНАМИЧЕСКИХ СИСТЕМ*

А. А. Шестаков, О. В. Дружинина

В настоящей статье обсуждаются результаты качественного исследования в целом динамических систем. Охарактеризованы некоторые перспективы применения указанных результатов для изучения математических моделей естествознания и техники. Рассмотрены вопросы об устойчивости и об условиях существования притягивающих и отталкивающих областей силового поля.

Проблемам качественного исследования в целом динамических систем начиная с работ А. М. Ляпунова [8], А. Пуанкаре [20], Ж. Ада-мара [22] посвящены многочислешгые работы [1-7; 9-19; 21; 23 и др.].

Отправляясь от идеи второго метода Ляпунова исследования устойчивости, рассматриваемой в геометрическом аспекте, а также от идеи метода Пуанкаре топографических поверхностей, Н. Д. Моисеев [11-13] развил метод качественного исследования динамических систем, названный им методом характеристик контактов. Сообщение об этом методе Н. Д. Моисеев сделал на Втором Всесоюзном математическом съезде в 1934 г. Метод характеристик контактов представляет собой обобщение метода, разработанного Ж. Адамаром в 1897 г. для обратимых динамических систем. Н. Д. Моисеев разработал метод для необратимых динамических систем.

Независимо друг от друга Ж. Адамар и Н. Д. Моисеев разработали два варианта второго метода Ляпунова качественного исследования в целом динамических систем, опирающиеся на использование пробной (вспомо гательной) функции и ее первой и высших орбитальных производных в силу дифференциальных уравнений. Эти варианты назовем соответственно первым и вторым вариантами дифференциального метода Адамара-Моисеева качественного исследования динамических систем. Метод Адамара—Моисеева получил значительное развитие в трудах московской научной школы В. В. Немыцкого [1— 2; 7; 9-10; 14-19; 21]. С этими работами тесно связаны работы [4-6].

Поставим вопрос о характере изменения функции вдоль траектории, описываемой точкой, движущейся согласно дифференциальным уравнениям первого порядка

ДГ}

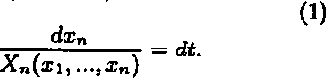
С этой целью запишем вычисленную в силу уравнений (1) полную производную от пробной функции V(xi, ...,т_ге) по времени t

@ А. А. Шестаков, О. В. Дружинина, 2010 ’Работа выполнена при поддержке РФФИ (проект № 10-08-00826-а).

dV dt

av

8x;

dV 8x2

dV

Sx^

= W), являющуюся некоторой функцией от фазовых координат (xi,..., т„).

Приравнивая это выражение нулю, получаем уравнение поверхности

X(V) = 0,             (2)

являющееся геометрическим местом контактов траекторий с семейством топографических поверхностей V = const или же геометрическим местом точек пространства R?, в которых возможно достижение экстремума функции V при движении вдоль траектории уравнений (1).

Далее рассматривается вторая производная пробной функции V, вычисленная также в силу уравнений (1):

d²V _ дХ(У) dt² 8xt ¹

—---Л 2 + ... + 0X2

^-^^Ха-ХХ^), являющаяся также некоторой функцией от фазовых координат. Приравнивая ее нулю, получим уравнение другой поверхности в фазовом пространстве

XX(V) = 0.

Поверхность (3) пересечется с поверхностью контактов (2) по некоторой линии

Х(У) = О, XX (У) = 0,       (4)

называемой оскулатрисой.

Оскулатриса (4) разделяет поверхность контактов (2) на две части; для одной из этих частей справедливы соотношения

Х(И = 0, XX(V)<0,      (5)

для другой части справедливы соотношения

Х(К) = О, ХХ(У) > 0.      (6)

Если рассматривать функцию V как сложную функцию времени t, зависящую от времени через посредство координат точки М, двигающейся согласно уравнениям движения (1), то все максимумы такой функции могут достигаться только в точках части пространства, которая определяется неравенством

XX(V) < 0, (7)

или же только в точках совокупности областей (4) и (5). Все минимумы функции V могут достигаться только в области, в которой

ХХ(У) > 0, (8)

или же - более точно - в области, являющейся совокупностью (4) и (6). Справедливы следующие.

Теорема 1 [22]. Рассмотрим дифференциальные уравнения первого порядка вида (1). Пусть при. движении точки М по фазовой траектории уравнений (1) (при изменении t от to до оо) пробная функция V будет иметь, вообще говоря, бесконечное множество последовательных максимумов и минимумов. Каждая траектория, вообще говоря, должна пересекать бесконечное число раз поверхность контактов (Й), переходя при этом из одной части (7) этой поверхности в другую (8).

Теорема 2 |22]. Рассмотрим динамическую систему, определяемую уравнениями вида. (1), для которой функции Xi и их производные до второго порядка являются ограниченными. Пусть пробная функция У(г1,...,г_п) и ее производные до третьего порядка остаются ограниченными при неограниченном возрастании t и не имеют при возрастании t бесконечного числа экстремумов. Тогда У($1,..., т_п) асимптотически стремится к оскулатрисс (Д), в том смысле, что по крайней мере для одной из траекторий значение V(xi,..., т_п) с возрастанием времени t произвольно близко подходит к любой точке оскулатрисы.

Будем называть метод качественного исследования, использующий теоремы 1 и 2, первым (фазовым) вариантом метода Адамара-Моисеева. Теоремы 1 и 2 вносят существенный вклад в обобщение и систематизацию методов общего качественного анализа применительно к задаче движения точки в фазовом пространстве и к случаю, когда уравнения движения являются дифференциальными уравнениями первого порядка вида (1). Они представляют большую ценность для теории устойчивости, так как с их помощью в ряде случаев можно легко решать вопрос о неустойчивости заданного состояния равновесия.

Кроме того, Адамар разработал второй (координатный) вариант рассматриваемого метода качественного анализа. В этом варианте речь идет не о фазовом, а о координатном пространстве, в котором движется точка. Уравнения движения записываются в ви- де лагранжевых уравнений второго порядка, разрешенных относительно вторых производных от координат по времени. Пробная функция выбирается здесь зависящей только от координат, а не от координат и компонент скорости, как это было в фазовом варианте. Но идея метода остается прежней, а именно при помощи второй орбитальной производной от пробной функции по времени, вычисленной в силу дифференциальных уравнений движения, и при помощи условия равенства первой производной нулю стремятся получить областную качественную характеристику или функцию точки в пространстве движения. Знак указанной функции дает возможность различать области возможности максимумов пробной функции от области возможности минимумов той же функции, рассматриваемой как сложная функция времени, зависящая от него через посредство координат движущейся точки.

Отличие исследования А. Кнезера [23] от исследования Ж. Адам ара [22] состоит в том, что Адамар вычисляет вторую производную от пробной функции при условии равенства нулю первой производной, тогда как Кнезер этого условия равенства первой производной нулю не использует. Этот факт существенен, так как дает возможность получить вторую производную в виде областной характеристики в пространстве движения, в виде функции точки этого пространства, тогда как в работе Кнезера вторая производная зависит не только от координат, но и от скоростей изменения этих координат. Для получения характеристики Адамара как функции точки в обычном пространстве одного условия равенства нулю первой производной недостаточно. Нужно привлечение еще иных дополнительных условий. Адамар рассмотрел случай задачи движения точки в поле консервативной силы, допускающей потенциальную энергию, зависящую только от координат, причем число степеней свободы равно двум. В этом частном случае для выражения второй производной от пробной функции через одни только координаты оказывается достаточным использовать, кроме условия равенства нулю первой производной, еще интеграл энергии. Это дает два уравнения, из которых компоненты скорости определяются через координаты и постоянную интеграла энергии. Два дифференциальных уравнения движения дают выражения вторых производных от координат через координаты. С помощью этого вторая производная от пробной функции может быть выражена через одни координаты и через постоянную интеграла энергии. В результате получается величина, которую Н. Д. Моисеев назвал характеристикой контактов траекторий данного изоэнер-гетического семейства с кривыми топографической системы.

Далее в координатном методе устанавливается для каждого заданного значения постоянной энергии разбиение области возможного движения1 точки на две части. Одна из них является областью возможности максимумов пробной функции, другая - областью возможности минимумов. Каждая «неисключительная» траектория должна поочередно переходить из одной такой области в другую, бесчисленное количество раз пересекая оску-латрису.

Ж. Адамар [22] принял в качестве пробной функции именно потенциальную функцию задачи. С другой стороны, он рассмотрел движение точки не в плоскости, ио по некоторой кривой поверхности.

Теорема 3. Пусть существует по крайней мере одна неустойчивая координата. Тогда. движущаяся материальная точка, пребывающая. в окрестности состояния равновесия, где потенциальная функция не имеет максимума, отклоняется от этого состояния на конечное расстояние. Исключе ние может иметь место лишь: 1) для тра екторий, когда отклонения и скорости тех параметров, которые соответствуют состоянию неустойчивости, являются и продолжают оставаться достаточно малыми по сравнению с отклонениями и скоростями других параметров; 2) для траекторий, стремящихся асимптотически к рассматриваемому состоянию равновесия, достаточно близкому к равновесию, если таковое имеется.

Впрочем, вопросы существования и многообразия упомянутых здесь исключительных движений Адам аром не рассматривались.

В тех случаях, когда имеются только две степени свободы и потенциальная функция имеет минимум, А. Кнезер [23] установил наличие траекторий, асимптотических к положению равновесия. Очевидно, что в общем случае аналогичное рассмотрение было бы значительно более сложным. Так, например, через произвольную точку гиперболического параболоида не проходит траектория, стремящаяся асимптотически к вершине: единственной траекторией, представляющей этот вид, является парабола, находящаяся в осевом сечении и вогнутая снизу. Имеется в ви ду, что движение материальной точки проис ходит по поверхности гиперболического пара-2      2

болоида г = ---—, причем положительная 2р 2g ось г направлена вертикально вверх.

Рассмотрим далее общий характер дви жения консервативной голопомной системы. Для простоты примем, что материальная точка единичной массы движется по глад кой поверхности под действием сил с потенциалом П. Обозначим через пив парамет ры, определяющие точки на поверхности, элемент длины которой определяется формулой ds2 = Edu2 4- 2Fdudu + Gdu2, где E, F, G - заданные функции от и и -и. Точка обладает кинетической энергией Т = ^(^й2 + 2Ftti 4- Gv2). Рассмотрим на траектории голопомной системы точку, в которой потенциал П имеет минимум. Очевидно, что в этой точке П — 0 и вторая производная П в силу лагранжевых уравнений движения положительна. Если точка описывает траекторию, то пробная функция П либо принимает бесчисленное множество чередующихся друг за другом максимумов и минимумов (общий случай), либо начиная с определенной точки изменяется в одном направлении (частный случай). Допустим сначала, что имеет место общий случай. Разложим поверхность на две такие области, что в одной из них /п > 0, а в другой /п < 0, где /п -функция, имеющая стандартный явный вид. Из вышесказанного следует, что первая из этих областей содержит все точки траекторий, в которых П имеет минимум, т. е., вообще говоря, бесчисленное множество отрезков траекторий, каждый из которых имеет конечную длину. Но во второй области, где In < 0, материальная точка не может оставаться постоянно. Поэтому обе эти области называются в [22] соответственно притягивающей и отталкивающей областями. В общем случае существуют одновременно обе эти области, так как нетрудно показать, что все изолированные точки поверхности, в которых П имеет минимум, т. е. точки, в которых возможно устойчивое равновесие, принадлежат притягивающей области, а все точки, в которых П имеет максимум, принадлежат отталкивающей области.

Предположим теперь, что имеет место второй случай, т. е. что начиная с некоторо го момента времени функция П изменяется в одном направлении. Будем предполагать, что поверхность нигде не уходит в бесконечность и не имеет особых точек, а функция П правильна во всех точках поверхности. Так как функция П изменяется в одном направлении, то опа необходимо стремится к некоторому определенному пределу, а первая и вторая производные П и П стремятся к нулю. Следовательно, если на поверхности существует только конечное число состояний равновесия (что, как правило, действительно имеет место), то материальная точка приближается к одному из этих состояний со скоростью, стремящейся к нулю. Такое состояние равновесия будет неустойчивым, так как при обращении движения материальная точка, находясь в начальный момент вблизи состояния равновесия и имея малую скорость, будет с течением времени удаляться от этого состояния, что противоречит определению устойчивости. Таким образом, справедлива следующая теорема.

Теорема 4 [22]. Пусть материальная тонка свободно движется по поверхности, нигде не уходяи^ей в бесконечность и не име-ющей особых точек, пусть, кроме того, потенциальная энергия есть функция правильная во всех точках поверхности и имеет на ней только конечное число экстремумов. Тогда либо длина отрезка траектории, ле-жащего е притягиватои^ей области, превышает каждое заданное число, либо траектория асимптотически приближается к состоянию равновесия неустойчивого состояния равновесия.

Сравним заключение теоремы 4 с результатом при движении точки по заданной кривой под действием силы, зависящей только от положения. В этом случае точка либо описывает бесконечно большой путь в определенном направлении, либо колеблется около состояния устойчивого равновесия. Притягивающая область при движении с двумя степенями свободы соответствует состоянию устойчивого равновесия при движении с одной степенью свободы.

Описанные выше фазовый и координатный методы являются важными для практических приложений вариантами второго метода Ляпунова, причем фазовый метод целесообразно использовать для решения задач устойчивости неуправляемых и управляемых технических систем, а координатный метод - для решения задач устойчивости систем небесной механики. Фазовый метод ис- следования устойчивоподобных свойств в монографии [21] распространен па распределенные динамические системы различных типов (стохастические, нечеткие распределенные системы и др.)

Исследования В. В. Немыцкого, известного ученого и неутомимого пропагандиста качественных исследований в целом с помощью второго метода Ляпунова, содержатся в статьях [14-18], а исследования учеников и последователей В. В. Немыцкого - в [1-2; 7; 9-10; 19; 21] и др. работах. Идея о вращающей функции Ляпунова развита в [15]. С помощью вращающей функции возможно исследовать фазовые портреты траекторий в случае отсутствия асимптотической устой чивости. В. В. Немыцкий разработал общий метод качественного исследования в целом свойств траекторий на плоскости при наличии одной особой точки и предложил топологическую классификацию особых точек и обобщенных функций Ляпунова. Е. А. Барба-шин [1-2], развивая идеи работ В. В. Немыцкого о структуре вполне неустойчивых динамических систем, показал, что вопрос о нахождении простейшей структуры выпрямляемой системы решается вторым методом Ляпунова. Пользуясь методами В. В. Немыцкого, его ученики и последователи внесли весомый вклад в качественные методы исследования в целом траекторий динамических систем с помощью второго метода Ляпунова.