О регулярной ходьбе экзоскелетона нижних конечностей при дефиците управляющих воздействий

Исследование усилительных систем типа экзоскелетона впервые было инициировано компанией General Electric в конце 1960-х гг. в рамках полноразмерного экзоскелетона с 30 степенями свободы, называемого «Хардимен» [9]. «Хардимен» был разработан с целью увеличения способностей солдат по переноске и подъему грузов. Однако проект не был успешным из-за большой массы экзоскелетона и несовершенной системы управления. В последние десятилетия интерес исследователей к организации двуногой ходьбы постоянно возрастал как в области биомеханики, так и в области робототехники. Научный анализ двуногой ходьбы позволяет лучше понять особенности человеческой походки и ее объективные свойства, а также вносит потенциальный вклад в проектирование и разработку экзоскелетонов – мобильных устройств, помогающих перемещаться человеку. Такие устройства необходимы и для организации движения ног человека, потерявшего полную или частичную способность двигаться самостоятельно в результате травм, а также они необходимы для обеспечения перемещения груза по сложной пространственной траектории.

Наиболее сложной и важной является проблема разработки системы управления экзоскелетоном нижних конечностей, который способен обеспечить перемещение по заданной траектории. Экзоскелетоны, как правило, описываются и моделируются как двуногие роботы, управляемые человеком. Двуногий робот, перемещающийся в сагиттальной плоскости, может рассматриваться как плоская кинематическая цепочка, состоящая из двух ног и туловища. Ноги одинаковы и симметричны и соединены с туловищем в бедре. Каждая нога состоит из двух звеньев – верхнего (бедро) и нижнего (голень), соединенных посредством колена. Стопа обычно рассматривается как третье безмассовое звено. Таким образом, рассматриваемый механизм является семизвенным. Цикл ходьбы состоит из одноопорной и двуопорной фаз. На одноопорной фазе движения, называемой также фазой переноса конечности, только одна стопа находится в контакте с землей. В этом случае математическая модель представляет собой кинематическую цепь с пятью степенями свободы, в каждой степени которой формируется некоторый момент. Если на земле находятся обе ноги, то число степеней свободы уменьшается до трех, но возникают дополнительные кинематические соотношения. Движение робота представлено на рис. 1.

Целью настоящего исследования является аналитический синтез законов управления движением человека, интегрированного с экзоскелетоном посредством двигателей, расположенных в тазобедренном и коленном шарнирах, которые позволяют реализовать желаемое движение человека в сагиттальной плоскости как в одно-, так и в двуопорной фазах. Синтез строится на основе динамических уравнений механизма, моментные двигатели считаются идеальными.

Д инамическая система и уравнения движения

Рассматривается задача управления биомеханизмом – человеком, интегрированным с экзоскелетом, при перемещении его по ровной горизонтальной поверхности в режиме плоской ходьбы. На рис. 1 показана схема тела человека с аппаратом и введены обозначения углов и моментов M _{i , j} ( i = 1; 2; j = 1; 2; 3) в суставах; в стопах ног в точках ( x _{1 p} , y _{1 p} ) и ( x _{2 p} , y _{2 p} ) точечно приложены силы реакции R . Определяющими координатами динамической системы являются ( x , y ) – координаты тазобедренного сустава, а также углы звеньев экзоскелетона с вертикалью (ψ, α₁, β₁, α₂, β₂) .

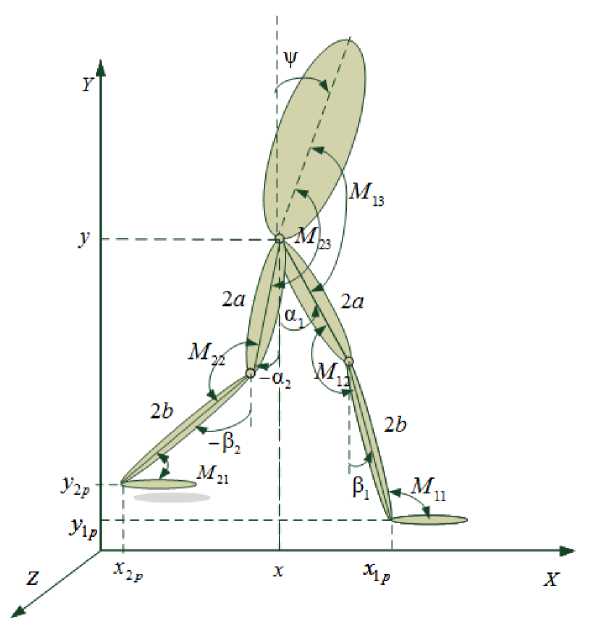
Рис. 1. Схема человека с экзоскелетоном в движении

Используя метод Лагранжа, получим следующую систему уравнений [1, 2], описывающую движение аппарата:

Mx + K_r ( V cos у - V 2 sin V ) +

>Z {Ka (ai cos ai - ai2 sin ai)+ Kb (в cos Pi - в^ sin вi )} = Qx, i=1

My - K_r ( V sin v + V 2 cos V ) +

⁺ E { ^Ka ( ^a i sin ^a i ^{+ a} i ² cos ^a i ) ^{+ K}b ( ^в sin P i ^{+ e} i ² cos P i ) } = ^Qy - ^M g ^, i =1                                                                                                                  ⁷

J V - K _r ( y sin V - x cos V ) - gK _r sin V = Q _V ,                      ⁽³⁾

JX + Jab Pi cos ( ai - Pi ) + Ka ( x cos ai + y sin ai ) + + JabP2 sin ( ai - Pi ) + gKa sin ai = Qai , i = 1; 2,

^Jb P i ^{+ J}ab ^a i cos ( ^a i - ^в ) ^{+ K}b ( ^X cos ^{в +} y sin ^в ) -- ^Jab^{a 2} sin ( ^a i - ^в i ) ⁺ g ^Kb sin ^в i = ^Qei , i = 1; ² .

Здесь обозначено

2 Q = Z R x -I = 1

Q, =Z R, - i =1

Q , =— Z M i3 -                                (6)

i = 1

Q a . = — ^Mi2 — M 3 + ² a ( ^Rix cos ^a i + ^Riy sin ^a i ) ^-

Q_R = M,, + 2 b Г R. cos в, + R , sin в,) + M= , - β          2              x                y                   1

где g – ускорение силы тяжести; R _x , R _y – силы реакций опоры; 2 a и 2 b соответственно длины бедер и голеней; m_a , m_b – их массы; m_t – масса корпуса; r – расстояние центра масс корпуса от таза; a , - b , - соответственно расстояния центров масс бедра и голени от таза и коленей ног; J и J_a – моменты инерции соответственно корпуса и бедра относительно точки таза; J_b – момент инерции голени относительно колена.

Обозначим также

M = m_t + 2 m_a + 2 m b -

*2

^Ja = J a ^{+ 4} m b^{a -}

K a = m a^a , ^{+ 2} m b^{a -}

Kb = mb - Jab = 2mM - Kr = mr•

Уравнения (1)–(6) пригодны для описания движения как с одноопорной (с мгновенной двуопорной фазой), так и с протяженной двуопорной фазой, а также для режима, где сочетаются обе фазы. В дальнейшем под номером один всегда будет пониматься передняя опорная, а под номером два – задняя (переносимая) нога.

Если рассматривается одноопорная ходьба, то количество переменных переопределено, так как координаты таза могут быть выражены через углы опорной ноги:

x, - x = 2a sin a, + 2b sin p,- p                                                                  (7)

y - ,1 p = 2a cos a1 + 2b cos P1- причем можно считать, что x1 p = ,1 p = 0 . Дифференцируя соотношения (7), нетрудно получить выражения для первых и вторых производных по координатам x и y. Используя формулы (7), можно также в случае одноопорной ходьбы заменить выражения x и , через первые и вторые производные углов a1, в1, выразить через них силы реакции в опорной ноге R1x,R1y и, подставив все это в соотношения (3)–(5), получить замкнутую систему из пяти дифференциальных уравнений. В компактной форме эта система уравнений имеет вид [8]

B ( z )|| z || + D ( z )|| z ²|| + Ag\ |sin z || = C||M ,3 - M _B- M ₁₂- M 22 - M ,,|| ^r ,              (8)

где ||z|| = Цу- a,- a2- в,- в2||Г - а B(z)-D(z)- A-C - некоторые матрицы- зависящие от масс-инерционных характеристик человека и экзоскелетона. Пусть все звенья тела человека и, соответственно, экзоскелетона весомы за исключением стоп. Считается, что моменты M.j (i = 1; 2; j = 2; 3) вырабатываются двигателями экзоскелетона, а человек поддерживает только вертикальную позу. Величины масс-инерциальных характеристик тела человека и экзоскелетона, используемые в численных экспериментах, указаны в прил. 1.

П остановка задачи

Под действием управляющих моментов M i j ( i = 1; 2; j = 2;3) механизм совершает предписанное движение. Построим систему управления экзоскелетоном, используя только четыре двигателя, развивающие управляющие моменты M ₁₃, M ₂₃, M ₁₂, M ₂₂ . Что касается стопных моментов M ₁₁, M ₁₂ , то они приняты пассивными, т.е. реализуются в фазе опоры соответствующих ног с помощью идентичных крутильных пружин с подбираемой жесткостью и нейтральной угловой длиной; в фазе переноса ноги пружина в стопе фиксируется и M ₁₂ = 0. Такая схема управления технически более выгодна, поскольку позволяет иметь меньшее число управляющих моментов. Оценим, к каким погрешностям в конце одного шага регулярной ходьбы приведет синтезируемый алгоритм управления на примере «желаемого», комфортабельного движения [1, 2] с известным периодом шага T , длиной шага L и высотой перемещения точки таза h .

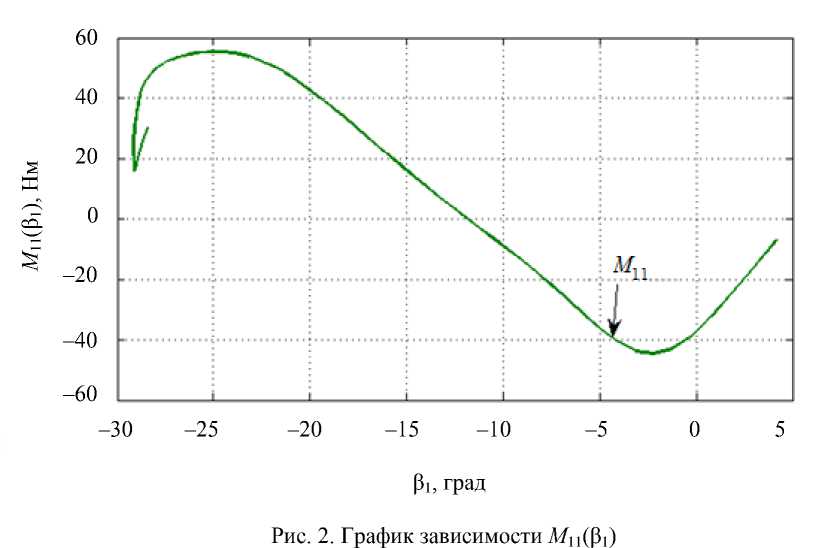
Проведенные исследования [6] показали, что зависимость момента в голеностопе от угла между голенью и стопой приближенно носит кусочно-линейный характер. На рис. 2 приведен график этой зависимости M ₁₁(β₁) при параметрах L = 50 см, h = 86 см, T = 0,7 с в случае одноопорной ходьбы. Угол с горизонтом в опорной стопе также определяется углом в ! , он равен в 1 + п / 2 .

Из рис. 2 видно, что за исключением короткого начального отрезка фазы опоры ноги (с точки зрения реальной ходьбы человека это, скорее, фаза двуопоры) при в 1 ^ - 5° управляющий момент M ₁₁ растет, в то время как угол β₁ убывает. Отметим, что такая общая тенденция отвечает пружине с отрицательным коэффициентом жесткости.

С лучай одноопорной ходьбы

Поскольку остальные степени свободы, кроме стопы опорной ноги, управляемы, примем для них следующий закон управления [6]:

^1 _O ⁽ t ) = ^а1 ⁽ t ) - ^ai* ⁽ t ) = (^ 11 + ^X12 X^a 1 ⁽ t ) - ^a 1* ⁽ t)) - ^ 11 ^ 12 ^(ai ⁽ t ) - ^ai* ⁽ t )X

ё_2а ( t ) = a₂ ( t ) - a₂ * ( t ) = (X₃₁ + X₃₂ )(a₂ ( t ) - a 2 ( t )) - X₃₁X₃₂ (a₂ ( t ) - a₂ * ( t )), ^ ( t ) = в 2 ( t ) - 0 2* ( t ) = (X 41 + X 42 )(0 2 ( t ) - 0 2* ( t )) - X 41 X 42 (в₂ ( t ) - в 2* ( t )),

ё_¥ ⁽ t ) = V ⁽ t ) ^- V ⁽ t ) = ⁽ Y 1 ⁺ Y 2 Xv ⁽ t ) ^{- V} *⁽ t )) ^- Y 1 Y 2 ⁽ V ⁽ t ) ^- V *⁽ t ))•

Здесь λ, γ – отрицательные константы; углы с верхним индексом «*» отвечают желаемому комфортабельному типу движения, определяемому следующими выражениями: по углам α ₁ ,β ₁ соотношениями (7) при

x* = Vt - о, y *= h , V = L / T , о = L /2; x 1 _p = y 1 _p = 0,                (10)

по углам α 2 , β 2 [3, 4]

x 2 p =- L cos(Q t ), y * p = 5²sin²(Q t ), Q = n / T ,                  (11)

«желаемой» кинематике таза [1, 3, 4]:

*         ₊ ^{x -} xp 1

a 1 =- arctg—----

У ^- У р 1

+ arctg

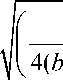
4ad a2) - d2

β 1

= - arctg

*

■ - x p 1

*

У - У р 1

-

arctg

I (    4 bd ^—

\(4( a² -b ²) - d²

^- 1,

^- 1,

где δ - некоторая константа, задающая высоту траектории переносимой ноги (обычно 6 ² = 0,02 м) и, наконец, по углу v [2]

ML Й ( t ) =- 2 K r

1 + ch® T    1 Mx *       L 2     Krg ch® t --sh® t --, о = —, to2 =---- r ---.        (12) L        sh® T      J   Kr       2        J + Krh

Приведем явные формулы, определяющие поведение углов aj, 01 при заданной где d = ^(x* - x1 p )2 +(y* - У1 p )2.

Формулы (13) легко могут быть получены из условий (7).

Для синтеза закона управления определим, какой информацией располагает система управления. Будем считать, что в шарнирах экзоскелетона установлены сенсоры, определяющие углы и угловые скорости v, a 1 , a₂, 0 i , в₂, V, a 1 , a₂, 0 i , в₂ экзоскелетона. Углы в шарнирах экзоскелетона и их угловые скорости могут быть определены с помощью инкрементных или абсолютных датчиков, а также инклинометров и акселерометров. Примем, что углы и угловые скорости в суставах человека совпадают с соответствующими переменными экзоскелетона, так как положение человека жестко фиксировано относительно экзоскелетона.

Определим величины потребных моментов, которые должны развивать приводы экзоскелетона, используя уравнения динамики (8) одноопорного движения и управляющие соотношения (9). Поскольку стопный момент M ₁₁ известен:

M 11 = c (в 1 - в 0 ) , (14) где c – жесткость пружины; β ₁ ⁰ – ее нейтральная угловая длина, и, наоборот, величина в 1 неизвестна, то уравнения (8) можно переписать в следующей форме:

B i ⁽ z )|| w || + D ( z )| z ² 11 + BAg ||s ⁱⁿ z || = C l M ₁₂, M ₂₂, M !3 , M 23 , ^l ^Г .

Откуда находим

I M 12 , M 22 , M 13 , M 23 , &| \ ^T = C ^{- 1} [ Ё ( z )| P I + D ( z )|| z ²|| + Ag |^in z\ I] .         (15)

Здесь ||w || = | |\|7, &i, a₂, M _m Р2Ц и, по-прежнему, ||z || = | p, « 1 , « 2 , P i , P 2I Г • Подставляя эти векторы и их производные в правую часть соотношений (15), получаем явный вид неизвестных моментов и второй производной 0 1 как функций времени. Конкретный вид матриц A , (2 , Ё ( z ), B) ( z ) приведен в прил. 2.

Построенный алгоритм был промоделирован для различных вариантов кинематики комфортабельного движения в широком диапазоне величин жесткостей c и нейтральных длин β ₁ ⁰ пружины, отвечающей развиваемому моменту M ₁₁ . В приведенной ниже табл. 1 детально проанализированы различные варианты этих расчетов, относящиеся к случаю крутильной жесткости стопной пружины c = - 100 Нм. Согласно рис. 1 положительный момент M ₁₁ является распирающим, т.е. он отталкивает голень от стопы опорной ноги, покоящейся на поверхности перемещения. При принятых величинах параметров походки h , L , T подбирались угловые значения ненагруженной пружины β ₁ ⁰ для обеспечения наилучшей точности в конце шага. В качестве критерия точности ρ было выбрано выражение

Р = V [ ^ ( Г ) - L /2]² + [ y ( Г ) - h ]² + [ X p 2 ( T ) - L ]² + [ У р 2 ( T )]²,              (16)

представляющее собой точность реализации требуемого положения таза и переносной ноги в конце одиночного шага при периодической ходьбе. Аппарат считался нагруженным дополнительным грузом в 100 кг.

Таблица 1

Таблица выбора величины β ₁ ⁰ и отвечающего ей критерия качества ρ

h	L	T	β 10	ρ	h	L	T	β 10	ρ
86,5	50	0,7	-0,177	0,0015	82	60	0,7	-0,228	0,0205
85	-	-	-0,197	0,005	80	-	-	-0,248	0,009
84	-	-	-0,207	0,023	86,5	50	0,75	-0,16	-0,012
82	-	-	-0,228	0,0205	85	-	-	-0,18	0,0018
80	-	-	-0,248	0,02	84	-	-	-0,19	0,026
86,5	40	-	-0,171	0,0205	82	-	-	-0,21	0,032
85	-	-	-0,189	0,002	80	-	-	-0,247	0,0008
84	-	-	-0,2	0,0012	86,5	-	0,65	-0,195	0,014
82	-	-	-0,22	0,004	85	-	-	-0,217	0,0028
80	-	-	-0,239	0,009	84	-	-	-0,229	0,0005
86,5	55	-	-0,17	0,007	82	-	-	-0,25	0,0178
85	60	-	-0,188	0,0009	80	-	-	-0,268	0,0064
84	-	-	-0,204	0,014	-	-	-	-	-

Значения h , L , ρ з десь дан ы в санти м етрах, ве л ичина T – в секу н дах, β ₁⁰ – в радианах. Заметим, что высота т аза аппарата над п о верхност ь ю переме щ ения при пол н остью распрямлен н ых ногах составляет 91,6 с м . Наиме н ьшее из указанных значений h отвечает состоянию лег к ого прис е да (характерному дл я человека, несущего достаточно большой доп о лнительн ы й груз).

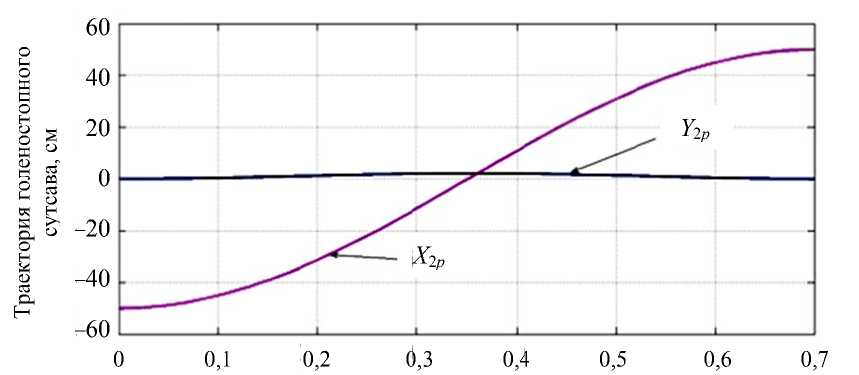
Критерий ρ пок а зывает то ч ность д о стижения конечног о положе н ия таза и пер е носимой ноги. Ниж е приведе н ы графики угла на к лона кор п уса ψ и т раектория пер е носимой ноги (рис. 3, 4), соо т ветствую щ ие пара м етрам, пр и веденны м в первой строке табл. 1.

Представленные выше р е зультаты вычисле н ий гово ря т о во з можности отр а ботки алгоритмом у п равления желаемой кинемати к и с весь м а высоко й степенью точ н ости, в частности поэтому н а рис. 3 и 4 предст а вленные г рафики ж елаемой и реальной траекторий сов п адают.

При той же величине жес т кости пружины алг о ритм поз в оляет об е спечить с высокой точностью кон е чное поло ж ение таза и переносной ноги и в случае нагрузки мех а низма меньшим вес о м, о чем г о ворят рез у льтаты, п р едставлен н ые в табл. 2.

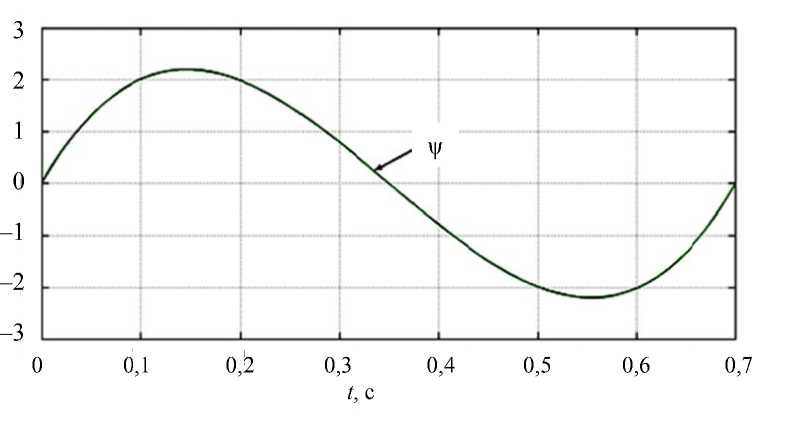
Рис. 3. Гр а фик завис и мости угла наклона ко р пуса от вр е мени

t , c

Р и с. 4. Графи к траектор и и переноси м ой ноги

Таблица 2

Таблица выбора величины β ₁ ⁰ и отвечающего ей критерия качества ρ при разных значениях переносимого груза

Нагрузка, кг	h	L	T	β 10	ρ
75	86,5	50	0,7	-0,196	0,0016
-	84	-	-	-0,229	0,0008
-	82	-	-	-0,249	0,0038
50	86,5	-	-	-0,196	0,0054
-	84	-	-	-0,2287	0,0037
-	82	-	-	-0,249	0,0051

Обращает на себя внимание, что в сходных вариантах расчетов при разных нагрузках от 100 до 50 кг величины 0 0 , реализующие указанные в последних столбцах обеих таблиц малые значения ρ, практически неизменны. Таким образом, в широком диапазоне нагрузок можно использовать пружину постоянной жесткости, например c = -100 Нм, немного подстраивая только параметр 0 0 по мере изменения кинематических параметров h , L , T . Отметим, что исследование выявило также высокую достижимую степень точности и в широком диапазоне величин жесткости от c = -200 Нм до c = 100 Нм, исключая случай полного отсутствия пружины, т.е. при жесткости c = 0 и в окрестности этого значения. При c = 0 и тех же величинах нагрузок и параметров h , L , T соответствующие значения ρ колеблются в полосе от 0,044 до 5,2 см, причем наименьшие значения ρ, как правило, отвечают только высоте h = 86,5 см, т.е. когда движение осуществляется при достаточно высоком положении таза.

Несколько слов о диапазоне подстраиваемых величин 0 0 , при которых достигается хорошая точность реализации конечного положения. Согласно табл. 1 и 2 он равен [-0,2675; -0,16] рад, т.е. его ширина (разброс) при c = -100 Нм порядка 6°. Однако высокая точность отработки реализуется в довольно узкой полосе величин 0 0 вблизи тех значений, которые указаны в вышеприведенных таблицах. Например, при реализации кинематических условий из верхней левой строки в табл. 1, значения ρ меньше условного «барьера», который примем в 0,25 см, только в полосе порядка 1,8° (0,031 рад) вблизи указанного в таблице значения 0 0 = 0,1768. Отметим также, что разброс при положительных значениях жесткостей c заметно больше, а полоса диапазона «барьера» несколько меньше, чем в случае отрицательных величин c . Так, например, при с = 100 Нм разброс составляет около 15° (0,26 рад), а ширина, отвечающая «барьеру», примерно 1,6° (0,028 рад). Причина этого кроется, видимо, в том, что согласно графику управляющего стопного момента опорной ноги на номинале (см. рис. 2) отрицательные жесткости способны отразить его желаемое поведение заметно лучше, нежели положительные.

С лучай совместной двуопорной и одноопорной фаз ходьбы

Рассмотрим один шаг аппарата, в котором сочетаются и двуопорная, и однопорная фазы движения, точнее, будем считать, что при t ≤ τ обе ноги находятся на поверхности перемещения, а при τ < t ≤ T на опоре находится передняя нога, а задняя участвует в переносе.

Построение алгоритма управления на двуопорной фазе при наличии ненулевых воздействий M ,M,M,M,M,M,R,R,R,R заметно сложнее, чем на xyx y одноопорной. Существенным изменениям по разным причинам подвергаются формулы (9) и (13). Поскольку теперь обе ноги находятся на поверхности перемещения, то соотношения (7) при x2p = -L, y2p = 0 применимы и ко второй ноге, а формулы типа (13) описывают также и поведение углов α2, β2. В связи с этим система соотношений (9), описывающая управление аппарата, изменяется и формально становится короче:

^a ⁽ t ) = ^а 1 ⁽ t ) ^{- а} 1* ⁽ t ) = (^ 11 + ^ 12 ) ^(а 1 ⁽ t ) ^{- а} 1* ⁽ t )) ^- ^ 11 ^ 12 ^(а 1 ⁽ t ) ^{- а} 1* ⁽ t )Х ё_¥ ⁽ t ) = ^ф( t ) ^- V ⁽ t ) = ⁽ Y 1 + Y 2 ^)(ф( t ) ^{- V} * ⁽ t )) ^- Y 1 Y 2 ⁽ V ⁽ t ) ^- V * ⁽ t ))•

**

Хотя желаемые величины по углам α2, β2 определяются условиями двуопоры, их реальные значения теперь зависят от реальных α1, β1, за формирование которых отвечают первое уравнение в (17) и момент в стопе первой опорной ноги M11 . Иными

**

словами, достаточно точная реализация величин α2, β2 не является гарантией соблюдения двуопорной фазы. Требование строгого соблюдения двуопорной фазы говорит о необходимости построения более сложного алгоритма управления.

Воспользуемся уравнениями системы (1)–(6). Это семь соотношений относительно 17 переменных, коими являются вторые производные от x, y, ψ, α₁, β₁, α₂, β₂ (всего семь) и M ₁₁, M ₁₂, M ₁₃, M ₂₁, M ₂₂, M ₂₃, R _{1 x} , R _{1 y} , R _{2 x} , R _{2 y} (всего десять). Для того чтобы найти все эти величины, необходимы еще десять дополнительных соотношений. Два из них даются в (17), еще два – это формулы для стопных пружин типа (14).

M 11 = c (Р , - e 0 ), M 21 = C (₽ 2 — e 2 ), в 0 = в 0 = в о .              (18)

Еще четыре соотношения можно получить, дважды дифференцируя

соотношения типа (7) в случае неподвижных голеностопных суставов обеих ног: x ip = x + 2 a (a i cos a i - a² sin a i ) + 2 b (в i cos в i - в 2 sin в i ) = 0, y_ip = y + 2 a (a i sin a i + a²cosa i ) + 2 b (в i sin в i + в²cosв i ) = 0, i = 1;2.

В сумме условия (17)–(19) дают восемь дополнительных соотношений. Наконец, устраним динамическую неопределенность в системе (1)–(6) за счет предположения о постепенной загрузке передней ноги и, соответственно, разгрузке задней. Обозначим через Rx, Ry суммарные силы реакции опоры, воздействующие на аппарат в точках контакта с поверхностью. Введем коэффициенты распределения нагрузки χ1 , χ2 , меняющиеся на интервале [0, 1]:

Х 1 ( t ) = ^{(т -} t )/ ^т , X 2 = ^1,2 Х 1 , R 2 x = X 2 R x ,

R 1 x = (1 - x 2 ) R x , R 2 y = X 1 R y ,

R 1 y = (1 - X 1 ) R y .

Рис. 5. Г рафики си л реакций в опорной н о ге

Соотнош е ния (20) показываю т , что реа к ции R_x , R_y в голен о стопах но г распред е лены по линейному закону во времени, одна к о этот закон один по горизо н тальной о си и другой – по вертикальной. П ричина р а зличия з а конов кр о ется в ф и зиологич е ской неодинак о вости поведения по осям x и y реакций, например, в передн е й ноге: п р и ее постанов к е на поверхность го р изонталь н ая реакция оказыва е т тормозя щ ее дейст в ие и становится даже отрицательной, в т о время к ак верт и кальная р еакция с т рого неотрицательна. На рис. 5 приведен ы график и [7] по в едения в е ртикальн о й и горизонтальной реакции при х о дьбе чел о века без груза.

Из рассмотрения этих графиков вытекает, что в мо м ент пост а новки оп о рной ноги суммарные вертикальная и горизон т альная ре а кции пол о жительн ы , в то вре м я как горизонтальная реакция на опорной но г е отрицательна. Эт о т факт и был учте н при конструи р овании функций χ₁ , χ₂ в фор му ле (20).

В сумме соотношени я (17)–(2 0 ) дают д есять требуемых д ополните л ьных соотноше н ий, чем полностью замыкае т ся весь алгоритм у п равления, а именн о при задании констант c , β₀ систе м а привед е нных выше соотношений позв о ляет найти все управляю щ ие моменты M_{i , j} ( i = 1;2; j = 2;3) .

Проведенные предварительные р а счеты по представленной мо д ели указ ы вают на необх о димость определенн о го уточн е ния модели угловог о движени я корпуса в (12) при рассмотрении шага аппар а та, на ко т ором сов м ещаются о дно- и дв у опорная ф азы. Угловое д вижение корпуса в э том случа е оказывает, как выя с нилось, с и льное вл и яние на резуль т аты расчетов.

Ф о рмула изменения в о времени угла ψ (12) была п о лучена в работе [1 ] при следующих предположениях: д вижение а ппарата к о мфортаб е льное, од н оопорное, ноги его неве с омы, стопы отсутс т вуют. В результат е в лине й ном при б лижении было проинтегрировано дифференц и альное у р авнение д ля ψ и н а йдено его периодич е ское с периодом T решение. Предполагая аналогич н о, что н оги аппа р ата неве с омы, в линейн о м приближении из (1)–(6) имее м (значок «*» ради к р аткости д а лее отбро ш ен)

R x = K r (у cos у - у 2 sin у) * K r У,

R y = Mg — k r (У sin У + У 2 cos У) * Mg , J У — gK r У = — M 13 — M 23 , M_t 1 — M_t 3 +

+ R ix (2 a cos a i + 2 b cos P i ) + R iy (2 a sin a i + 2 b sin в i ) = 0 ( i = 1;2).

При 0 <  t <  т на двуопорной фазе шага, ввиду x ₂ p = - L = - 2g, y ₂ p = 0 , имеем

2 a sin a 1 + 2 b sin P 1 = - x ,

2 a sin a 2 + 2 b sin в 2 = - x - 2g,

2 a cosa i + 2 b cosp i = y , ( i = 1; 2).

Поэтому из последнего соотношения в системе (21) вытекает, что m _n + m 21 + hR ; - xr; - 2gx i ( t ) r ; = m ₁₃ + m 23

или

( J + K r h )y - gK r У = - ( M 11 + M ₂₁) + Mg(Vt + g) - 2 M g gt I т.        (22)

В случае одноопорной фазы, когда т <  t <  T , данное выражение упрощается:

( J + K_rh )у - gK_r У = - ( M _п + M 21 ) + Mg (Vt - g).             (23)

Заметим, что в правых частях формул (22) и (23) стоят одновременно линейные функции времени и углов β₁, β₂. Это обстоятельство неудобно для аналитического исследования. Однако двуопорная фаза при ходьбе человека составляет малую часть общего времени шага и, кроме того, физиологические исследования говорят, что поведение каждого из углов β₁, β₂ на ней носит почти линейный характер по времени. Будем считать поэтому, что сумма стопных моментов (а на одноопорной фазе это просто момент M ₁₁ , о приближенной линейности по времени которого говорилось выше) носит кусочно-линейный характер. Формулы (22) и (23) тогда можно объединить, записав

( J + K r h )y - gK r у = - Mg <

• ^{- (} Vt + ^g) + ² t ^G + ⁽ ^ dt + ⁿ d )/ Mg , t <  т

τ                                (24)

• - (Vt - g) + [^ _s ( t - т) + n . ]/ Mg , T >  t >  т,

  •^

  
  

  •^

  
  

где ^ _d , n _d , относящиеся к фазе двойной ( double ) опоры, и ^ s , fj s , относящиеся к фазе одноопоры ( single ), косвенно характеризуют интенсивность суммарного стопного момента вместе со скоростью роста углов β₁, β₂; по физической сути они являются параметрами алгоритма управления, поскольку отвечают за поведение «желаемого» угла ψ^*. Введем в рассмотрение величины

« 2 = -gK- , J + hK_r

M σ ц =--- , v = ют

Kr и обозначим

^ d = ^ d / Mg ^G , n d = ⁿ d I Mg G ^ s = ^ s ¹ Mg G n s = n s / Mg g.

Тогда решение системы (24) на интервале двуопоры имеет вид

V = C 1 chto t + C ₂ shto t - ц

V 2

_V от   >

_ , _x I V 2

V = to( C 1 shto t + C ₂ chto t ) - ц I----

V о т

L d I t+1 - П d •

а в фазе одноопоры

V = D 1 chto t + D ₂ shto t - ц

— t - *)-L■ (t - T) - ns •

V = to( D 1 shto t + D ₂ chto t ) - ц I —

,

где C и D

-

произвольные постоянные. При t = τ эти решения должны быть

согласованы. Поэтому получаем

D ₁chtoт + D ₂shtoт = C ₁chtoт + C ₂shtoт + ц(L _d т + n _d - n _s )•

I 2 L - L

D 1 shtoT + D ₂chtoT = C 1 shtoT + C ₂chtoT + ц +      ^:

Tto to

s

,

или

L. - L

D 1 = C 1 - ц(- + ^^^ s )shv + ц(^ d т + n d νω

D 2 = C 2 + ц(- + ^ d-^s )chv - ц(^ d т + n d νω

В итоге строящееся решение приобретает вид при t ≤ τ

^- n s ) ^chv ,

- n _s ) shv.

V( t ) = C 1 chto t + C ₂shto t - ц

V 2

^^^^h         ^^^^h

στ

^L d I t ^{+ 1 -} П d •

при t > τ

I 2 L

V = C 1 chto t + C ₂ shto t - ц —+ — V v

d - L s

ω

( shv • chto t - chv • shto t ) -

^- ц ( ^ d ^{т +} n d

-

П _s ) ( shv • shto t - chv • chto t ) - ц ^— t - 1 + ц _ L _s ( t - т) + n _s ] ,

причем коэффициенты C 1 , C 2 должны определяться из условия его периодичности. Окончательно получаем следующие формулы для C 1 , отвечающие условиям периодичности:

+ d js

_V v 2to _v

( shv • chto T - chv • shto T ) - ц ( L _d т + n _d - n s ) ( shv • shto T - chv • chto T ) -

ц —

^ - T ^{- 2 +} n d

2 о

+2ц _Ls (T - t)+ns ]

shω T

1 - chto T

I 1 L_d — L

•<-ц — +

s

V ^v

2to _v

• (shv • shto T -

-chv • chto T) - ц ( L d т + n d - n s )•( shv • chto T - chv • shto T )-12 + L d - L s I -• 2 '                 '                                      2to V т             7

Аналогично для C 2 :

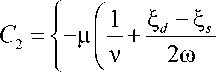
( shv • chto T - chv • shto T ) - ^— ( £ _d т + n _d

- n , ) ( shv • shto T - chv • chto T ) -

µ

V

-T - 2 + n d σ

+ JI[^,(T - т) + n,]••

shto T    [ ( 1

-------+ <-— - +

1 - chto T [ ( v

^ d - ^ , ]

2to J

x

x ( shv • shto T - chv • chto T ) - ^— ( ^_d т + n _d - n , ) ( shv • chto T - chv • shto T ) -—[ — + ^ _d - ^ ^ J > . 2 ^х               '                                2to V т            J

Данные соотношения являются заменой формулы (13) для случая совмещения одно- и двуопорной фаз движения. Параметры ξ _s , η _s , ξ _d , η _d , используемые в модели

(25) и отражающие приближенную физическую линейность во времени стопных моментов, могут рассматриваться одновременно как свободные коэффициенты настройки модели.

Ч исленное исследование алгоритма на шаге с одно - и двуопорой

При численном исследовании данного режима ходьбы величина τ полагалась τ = 0,17 c, что составляет приблизительно четвертую часть периода шага. Двуопорная фаза подразделялась на «чистую» двуопорную и «критическую», когда расстояние между голеностопом задней ноги и тазом превышало длину распрямленной ноги (или было близко к этому). Следует отметить, что при таком подходе «критическая» фаза заметно превышает по времени «чистую» двуопору, этот факт наблюдается и при физиологических исследованиях человека. В реальности «критическая» фаза предполагает сгибание стопы в плюснефаланговом суставе, что моделировалось подъемом по вертикали с переменной скоростью голеностопного сустава. При этом действие стопного момента на этой фазе в задней ноге сохраняется; на одноопорной фазе и стопный момент, и силы реакции опоры, естественно, считались равными нулю.

Исследование показало, что точность реализации алгоритмом, использующим четыре движителя, в смысле критерия (16) комфортабельного движения аппарата, существенно зависит от вида углового движения корпуса по ψ. Так, на модели углового движения (12) добиться приемлемых результатов не удалось. Модель же (25) дает заметно лучшие, технически приемлемые результаты. Так, например, в случае h = 86,5 см, L = 50 см, T = 0,7 c, c = -100 Нм, P0 =-0,21,

^ d = 0 c ^{- 1}, n d = 160, ^ , = 4 c ^{- 1}, n , = 94

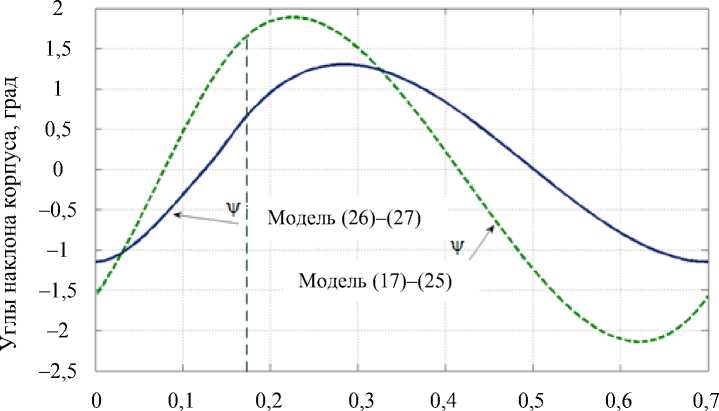
значение ρ составляет технически приемлемую величину 0,44 см. График функции ψ показан на рис. 6, корпус аппарата раскачивается вперед-назад в пределах порядка 2°, график периодичен. На пружинах другой жесткости при незначительном изменении параметров β0 , ηs удается получить величины ρ такого же порядка: при c = -150 Нм, когда n^ = 165, в0 = -0,223, величина p составляет 0,43 см, при c = -200 Нм, когда n5 = 170, в0 =-0,23, p составляет 0,425 см. Достаточно точно реализуется и периодическое движение корпуса по углу ψ. Сам угол ψ на данных решениях меняется в пределах у е[-0,037;0,033] рад.

Заметно лучшую точность реализации обеспечивает другая модель по углу ψ, также основанная на системе уравнений (1)–(6). От указанного выше подхода она отличается прежде всего модифицированной формой соотношений (17) на двуопорной фазе, вместо которых рассматривается

Ё1а ⁽ t ) = ^а 1 ⁽ t ) - ^а 1* ⁽ t ) = (^ 11 ⁺ ^ 12 ^)(а 1 ⁽ t ) - ^а 1* ⁽ t )) - ^ 11 ^ 12 ^(а 1 ⁽ t ) - ^а 1* ⁽ t )), i ^ 1p ( t ) = в 1 ( t ) - в ; ( t ) = <х_и+х₁₂)(в 1 ( t ) - в 1 ( t )) - ^ 11 ^ 12 (в 1 ( t ) - в 1 ( t )).

t , c

Рис. 6. Графики поведения угла наклона корпуса при разных моделях двуопоры

Тогда из дважды продифференцированных соотношений (7) мы имеем X, у . Поскольку аналогичные связи справедливы и для задней ноги, то известны и а₂, в 2 , а значит, и левые части в уравнениях (4), (5).

Пусть сумма их левых частей, распространенная на обе ноги, есть P . Складывая эти соотношения почленно, приходим к следующему условию:

P = ( M 11 + M 12 ) - ( M 13 + M 23 ) + yR ^ - xR ^ - Х 1 LR" _y . (27)

В соотношении (27) члены суммарной реакции R ^ , R y , а также M ₁₃ + M ₂₃ (с учетом условия (3)) известны с точностью до членов, содержащих линейную зависимость от второй производной у. Сумма M 11 + M ₂₁ задается формулой (19). Таким образом, условие (27) можно рассматривать как линейную связь между у их 1 . Если величину χ ₁ задать в виде линейной зависимости от времени, например, согласно формуле (20), то это определит некоторую величину у, а затем по цепочке уравнений (1)–(6) можно найти как функции времени и все остальные неизвестные переменные данной системы, в том числе и все управляющие моменты. Для этого надо только задать начальные условия у₀, у₀.

При переходе из фазы двуопоры в фазу одноопоры при t = τ теперь приходится, опираясь на достигнутые к данному моменту значения у(т), у(т), строить прогнозирующую траекторию для фазы одноопоры, обеспечивающую периодичность колебаний корпуса. При численном исследовании задачи она задавалась формулой со свободными, подбираемыми коэффициентами A , B , C , D :

у = A shw( t - т) + B chro( t - т) + C ( t - т) + D .

Приведем некоторые результаты численного исследования такого алгоритма. При тех же параметрах комфортабельного движения h, L, T, что и ранее, при c = -100 Нм, β0 = 0,3 величина ρ составляет 0,157 см; график соответствующей функции ψ показан на рис. 6, ему отвечают следующие начальные значения (в радианах и радианах в секунду): у0 = 0,02, у0 = 0. При c = -150 Нм, в0 = 0,11 имеем ρ = 0,078 см и примерно тот же диапазон колебаний по углу ψ; при c = -200 Нм, в0 = 0,01 имеем р = 0,036 см, а у е [-0,02;0,024] рад. Из сказанного выше можно сделать вывод, что наличие внутри периода шага еще и фазы двуопоры не сказывается существенно на точности предлагаемого алгоритма, найденного для случая одноопорной ходьбы, рассмотренного выше. Наличие двуопоры предоставляет человеку-оператору при известной тренированности определенный выбор угловых движений корпуса, при которых его воздействие на процесс движения может быть сведено к минимуму.

Б лагодарности

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (грант № 12-01-00800-а).

П риложение 1

При численном исследовании задачи в качестве модели тела человека была рассмотрена следующая среднестатистическая модель [5]: рост 174,7 см, вес 73,4 кг; длины бедер, голеней и корпуса соответственно равны 51,4; 40,2 и 74,1 см; их веса соответственно 9; 2,9 и 47,6 кг (вес стоп – каждая по 1 кг, высота голеностопного сустава над поверхностью 9 см); a , = 24,5 и b , = 16,1 см. Корпус человека считался равномерно распределенным по весу, исходя из этого подсчитывались величины K r и J . Значения других моментов инерции: центральный момент инерции бедра 0,1662 кг∙м², центральный момент инерции голени 0,0357 кг∙м². Масса экзоскелетона была принята равной 15 кг: 5 кг – вес корпуса, по 2,5 кг – вес каждого из бедер и голеней, причем их масса всюду распределена равномерно. Считалось дополнительно, что на корпусе экзоскелетона на высоте 45 см от таза закреплен груз весом от 50 до 100 кг. При исследовании использовались также следующие величины параметров математической модели: 5² = 2 см, X 1 = Y 1 = - 7 с^-1, х₂ = Y 2 = - 5 ^{с —} 1 -

П риложение 2

Ниже приведен вид матриц A , B ( z ), C , D ( z ):

	- Kr !	0	0	0	! 0
	0 \ка	- 2 aM	0	0	! 0_
A =	0_l	0	K a	0	'.
	0 '	0	0 K b	- 2 bM	! 0
	0 !	0	0 1                                                 1	0	। Kb

B =

J	- 2 aKr cos(a 1 + y)	0	...
2 aK r r cos(a 1 + y)	4 a ( a M - K a ) + Ja	- 2 aKa cos(a 1 - a2)	...
0	- 2 aKa cos(a 1 - a2)	* Ja	...
2 bKr cos(e 1 + y)	cos(a 1 - в 1 )(4 abM - 2 aKb - 2 bKa + Jab )	- 2 bKa cos(a2 - в 1 )	...
0	- 2 aK b cos(a 1 - в2)	J ab cos(a2 - e2 )	...

0 |-2 aKb cos(a 1 - в₂)

О | 7_аЬ ^сos[a2 ^- Р 2 ]

-1; - 2 ЬК ь cos^ - Р₂)

0            J b

■ 0   0 - 1 - 1

2 bK r cos(e 1 +v)

- 10  10 - cos(a ₁ - P 1 )(4 abM - 2 aK_b - 2 bK_a + J_ab )

C = 0 - 10  1 1000 0100

2 bK a cos(a 2 - в 1 )               , - 4 b ( bM - K b ) - Jb 2 bK b cos(e 1 - в 2 )             _

0 I              2aKr sin(v + a1)               '0

7T"^"-"7"-7-7-l----------------»“7

2 aK r sin(a₁ + v) !                      0                       j - 2 aK_a sin(a₁ - a₂)

D(z) =         0         ।             2aKa sin(a1 - a2)             '0

2 bK r sin(P1 + v) J - sin(a₁ - 01 )(4 abM - 2 aK_b - 2 bK_a + J_ab ) ] 2 bK_a sin(a₂ - 0₁)

⁰ I               ^{2 aK}b ^s in( ^a i ^- P2)              ! ^{- J}ab ^s in( ^a 2 - P2)

		2 bK r sin(v + 01)	0
		sin(a1 - 01 )(4 abM - 2 aKb - 2 bKa + Jab )	- 2 aKb sin(a1 - 02)
		- 2 bK a sin(a 2 - 01)	J ab sin(a 2 - 32)
1		0	- 2 bK b sin(01 - 02)
		2 bK b sin(01 - 02)	0