О решении краевой задачи типа Карлемана в классах обобщенных метааналитических функций в единичном круге

1. Об актуальности проблемы. Будем полагать, что С - плоскость переменного z = x + iy, а T + - односвязная область на С , границей которой выступает кривая Ляпунова L , причем z = 0 принадлежит T + .

Почти все основные термины и обозначения, используемые в данной работе, были приняты в монографии [1].

Комплексную функцию W ( z ) = U ( x,y ) + iV ( x,y ) переменного z = x + iy будем называть обобщенной метааналитической функцией в T + , если она в этой области является решением уравнения

d 2W (z)

a z ²

+A1 (z)

d W (z)

dz

+ A0 (z) W (z ) = 0,

a i f d

d

где — = —--+ i— , а Aiz} , A i( z ) - заданные голоморфные в T ⁺ функции.

a z 2 ^a x   d y у   ^o^    -                                        '

Определяющим характеристическим свойством всякой обобщенной метааналитической в области T + функции W ( z ) является то, что W ( z ) можно представить в виде

W ( z ) = [ ^ + ( z ) + z ^ + ( z )] e ^ ^z ) ^z , если A 0 ( z ) = Д ( z ) в T ⁺

или

W ( z ) = ^ ( z ) e ^^{( z} ) ^z + ^ ⁺ ( z )И^{1( z} ) ^z , если Л 0 ( z ) / Д ( z ) в T ⁺ ;

здесь ф ) ( z ), ф + ( z ) - так называемые голоморфные компоненты функции W ( z ) , являющиеся произвольными голоморфными функциями в T + , а ^ ) ( z ) и Д ( z ) - корни уравнения

2 2 + A 1 ( z ) 2 + A ( z ) = 0.                                  (4)

Функции вида (2) - обобщенные метааналитические функции первого типа, а функции вида (3) - обобщенные метааналитические функции второго типа.

Обозначим символом M ₂ класс обобщенных метааналитических в T + функций вида (2) или (3), у которых голоморфные компоненты ф ) ( z ) и ф ) ( z ), а также 2 0 ( z ) и Д ( z ) принадлежат классу A (T ⁺ ) n H ⁽¹⁾( L ).

Предлагается к исследованию следующая граничная задача K_M : среди всех функций класса M ₂( T ⁺ ) n H ⁽¹⁾( L ) найти те функции W ( z ) , которые удовлетворяют на L условиям :

F ⁺ И t )] = G 0 ( t ) F ⁺ ( t ) + g o ( t ),

^>1 = g, (tF( + g,( t),(6)

дn где —— производная по внутренней нормали к L, а(t) - прямой сдвиг контура L, для которого д n выполняется тождество

а[а(t)] = t,(7)

а G k ( t ) , g k ( t )( k = 0,1 ) - заданные на L функции класса H ^{( 1 )}( L ) ; здесь G_k ( t ) ^ 0 , a ( t ) ^ 0 и a ( t ) e H ( L ) .

Предложенная выше задача K_M - одна из основных краевых задач типа Карлемана для функций из класса M ₂ ( T ⁺ ) n H ⁽¹⁾ ( L ) .

В наиболее простом случае, когда а (t ) = t , задача K_M впервые была поставлена и изучена в [1].

В общем случае получить решение граничных задач типа K_M в классах M₂(T ⁺ ) n H ⁽¹⁾( L ) удается лишь методом интегральных уравнений [1, 2]. Но при таком подходе невозможно провести качественное исследование рассматриваемой граничной задачи, так как он не позволяет описать полную картину разрешимости такого плана задач и устанавливать их нетеровость. В связи с этим в настоящее время остается актуальной проблема отыскания частных случаев, когда рассматриваемая граничная задача допускает исчерпывающее исследование в явном виде [3, 4].

В настоящей статье устанавливается, что если T + - единичный круг, то задача K_M может быть решена в явном виде, то есть можно получить полную картину ее разрешимости, а также установить ее нетеровость. Ввиду схожести предлагаемой логической схемы для построения общего решения задачи K_M в единичном круге как для функций вида (2), так и для функций вида (3) в данной статье мы ограничиваемся детальным исследованием задачи K_M в единичном круге лишь в классе функций вида (2).

2. Построение общего решения задачи K_M в классе функций вида (2) в случае, когда

T ⁺= { z :| z | < 1} , L = { t :| t | = 1}

Во-первых, из представления (2) и соотношения [2, с. 304]

Э ДӘ -Э — — z t--1 —

Э n V Э t д t

Э

- 1— д t

-Э

-

t у, Э t

а также в силу выполнения тождества t — 1/ 1 на L — { t :| 11 — 1} условия (5) и (6) можно соответственно записать в виде

[ ^{а (}t ) ] 3 • ф + [ ^{а (} t ) ] ⁺ [ ^{а (} t ) ] ² • ф ⁺ [ ^{а (} t ) ] = G io ⁽ t ^)[ t ³ • Ф І ⁽ t ) ⁺ t ² • ф ^{+ (} t ^{)] +} g io ⁽ t ),             ⁽⁹⁾

Математика

d ^ o [ a ( t )]      d$idq( [ a ( )]             d L [ a ( t )]

[a(t)] —5---+ [a(t)] —h---+1 [a(t)] —---+ a(t)• ЛИt)] Ш«(t)] + dt                 dt \ dt                    J

+I a ( t ) • d ^ I ^ t )! + л [ a ( t )] + a ( t ) ] $ [ a ( t )] = <  dt                      J

(A /? d $ ⁽ t ) + ? d $ ⁽ t ) J z² d ^{L (} t ^)] + z HzAo+^W

= $ 11 ⁽ tt ⁺ t 1 ⁺ l t ⁺ t • ^{Л (} t ) I $ 0 ⁽ t ) ⁺ [ dt dt \ dt J

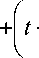
d A 0 [ a ( t )] dt

+ Л(t) +1 '$'(tU + gii (t), где

$ 10 ⁽ t ) = t ³ [ ^{a (} t ) ] ³ • $ 0 ⁽ t ) • exp { t • Л )⁽ t ) - ^{a (} t ) • Л [ ^{a (} t ) ] } ,

$11 (t) = t2 [a(t)]2 • $ (t) • exp{t • Л (t) - a(t) • Л [a(t)]}, gio(t) = go(t) • [a(t)]3 • exp{-a(t) • Л [a(t)]}, gn(t) = gi(t) • [a(t)]2 • exp{-a(t) • Л [a(t)]}. (11) Во-вторых, введя вспомогательные голоморфные в круге T += {z :| z | < 1} функции вида

Ф+ (z) = z $* (z) + z 2$+ (z),(12)

Ф+ (z) = z3d$0 (z) + z2d $ (z) + zz2 • d^°(z) + z^ (z$+ (z) + zz • ^^0(z) + Л (z) + z] $+ (z), (13) 1'-'                                                               О О                             О1

dz dz ^ dz j \ dzJ перепишем условия (9) и (10) следующим образом:

Ф+[a(t)] = $1o(t)Ф+ (t) + gw(t),te L,(14)

Ф + [ a ( t ) ] = $ 11 ( t ) Ф + ( t ) + g 11 ( t ), t e L . (15)

Выражение (14) - это граничное условие классической задачи типа Карлемана относительно функции Ф + ( z ). Сразу отметим, что в силу формулы (12) для функции Ф + ( z ) точка z = 0 является нулем не ниже 2-го порядка (то есть П {Ф + ;0} >  2). Выражение (15) является граничным условием классической задачи типа Карлемана относительно Ф + ( z ) [5, с. 172].

Предположим, что задачи типа Карлемана (14) и (15) разрешимы и найдены их решения -функции Ф+ (z) и Ф+ (z). Тогда, в силу (12) и (13), для нахождения голоморфных компонент $0 (z), $1 (z) искомой метааналитической функции W (z) =[$+ (z)+z$+ (z)]e^0^z)z (то есть для отыскания решения задачи KM ) нужно решить относительно $* (z), $+ (z) следующую систему: ' z $+ (z) + z $* (z) =Ф+ (z),

‘ ₃ d $ + ( z )    ₂ d $ + ( z ) ( ₂ d L ( z )     ₀         .,_x ( d L ( z ) □ z a A ₊z i ■, a ⁽¹ 6

z —0---+ z —1---+ | z —--+ zL(z) $0(z) + I z ——0--+ Л(z) + z I$1 (z) = Ф1(z)• dz dz ^ dz J \ dz

Решая систему (16), получаем:

$0 (z) = -W0+ (z), z e T+,(17)

2 z

$+ (z) = 1W+ (z), z e T+,(18)

2z где

^ dz              J z dz

W+ (z) = Ф+ (z) - (zd^z- + Л (z) - 3zA ^^ - d^, z e T+.(20)

^ dz               J z dz

Наконец, определим условия, при которых функции $ 0 ( z ), $ ( z ), задаваемые по формулам (17), (18), будут голоморфными в z = 0. Из формул (17) и (18) вытекает, что для этого голоморфная в круге T ⁺ функция W ₀ ⁺ ( z ) должна иметь в точке z = 0 нуль не ниже 2-го порядка, а для функции W 1⁺ ( z ) точка z = 0 должна быть хотя бы простым нулем, то есть П { W ₀ ⁺ ; 0} >  2, П {С ;0} >  1.

Пусть функции Ф ) ( z ), Ф ) ( z ) и Л ₀ ( z ) имеют следующие разложения в точке z = 0:

м  мм

Ф) (z) = z2^akzk , Ф) (z) = £bkzk , Л(z) = EPkzk, ze T+ .(21)

k=0                      k=0

Подставляя вместо функций Ф ) ( z ), Ф ) ( z ), J ( z ) их разложения (21) в правые части формул

(19) и (20), будем иметь:

м          /   м                 м            \ мм

W (z) = £bkzk - |z£k • Pkzk-1 + £Pkzk - z|£akzk - £(k + 2)akzk+1, k=0         \  k=1                k=0            J k=0

м         /   м                м             \ мм

W 1 ^{+ (} z ) = £ b k z k ^- 1 z £ k • Pkz k ^{- 1 +} £ P k z k ^- 3 z | £ a k z ^- £ ⁽ k ^{+ 2)} a k z ^{+ 1}.

k=0         У  k=1                k=0              J k=0

Из последних разложений видно, что условия П {W0+; 0} > 2 и П {W1+; 0} > 1 будут обеспечены, если выполняются равенства вида:

^b 0 ^- P 0 a 0 = ⁰, . b 1 - P 0 a 1 - ( 2 P 0 - 1 ) a 0 = 0.

Тем самым, установлена достоверность следующей теоремы.

Теорема 1. Если T ⁺ = { z : | z | <  1} является единичным кругом , то решение задачи K M в классе функций вида (2) сводится к решению двух классических задач типа Карлемана (14) и (15) относительно голоморфных в T + функций Ф ) ( z ) и Ф ) ( z ), причем задача K M в единичном круге разрешима тогда и только тогда, когда одновременно разрешимы вспомогательные задачи (14) и (15), а также выполняются условия (22) .

• 3.    О нетеровости задачи K M в случае, когда T⁺ = { z : | z | <  1} . Теорема 1 показывает, что картина разрешимости задачи K_M складывается из картин разрешимости задач (14) и (15).

В силу тождества (7) из краевого условия (14) можно получить равенство [5, с. 172]

( 1 - G _WM t )] • G J) )^ ф ; ( t ) = G J^ t )] • i j) + g _w[ a ( t )], t e L ,               (23)

а из (15) - равенство

( 1 - G [ a ( t )] • G © ) ^ Ф ) ( t ) = G [ a ( t )] • £j) + g „[ a ( t )], t e L .                (24)

Из (23) и (24) следует, что если хотя бы при одном из значений параметра k ( k = 0, 1) будем иметь 1 - G 1 _k [ a ( t )] • G _{1 k} ( t ) = 0, но G _{1 k} [ a ( t )] • g _{1 k} ( t ) + g _{1 k} [ a ( t )] # 0 , то задача K M неразрешима. Если же 1 - G _{1 k} [ a (t )] • G _{1 k} ( t ) / 0 и G _{1 k} [ a (t )] • g _{1 k} ( t ) + g _{1 k} [ a (t )] # 0 ( k = 0,1), то задачи (14) и (15) сводятся к задачам об аналитическом продолжении, а значит, не являются нетеровыми.

Но [5, с. 188] для того, чтобы обе вспомогательные краевые задачи типа Карлемана (14) и (15) были нетеровыми, необходимо и достаточно, чтобы функции G 1 _k ( t ), g 1 _k ( t ) ( k = 0,1) на L удовлетворяли следующим условиям:

1 - G ₁ k [ a ( t )] • G ₁ k ( t ) = 0 и G ₁ k [ a ( t )] • g ₁ k ( t ) + g ₁ k [ a ( t )] = 0 ( k = 0,1).                     (25)

Следовательно, на основании теоремы 1 и представления (2) получаем такой результат:

Теорема 2. Если область T + является единичным кругом , то для нетеровости задачи K M в классе функций вида (2) необходимо и достаточно выполнение условий (25).

Математика